基于TMR的磁导率EMT的传感器阵列设计

王 超，邹 萍，崔自强，何瀚辰，曹晴晴，王化祥



基于TMR的磁导率EMT的传感器阵列设计

王 超，邹 萍，崔自强，何瀚辰，曹晴晴，王化祥

(天津大学电气自动化与信息工程学院，天津 300072)

为实现对流化床中磁性催化剂颗粒分布的实时监测，对EMT技术应用于磁导率分布测量的可行性展开研究．常规EMT系统一般用于重建电导率分布，且采用线圈进行检测，存在检测灵敏度低、测量数据少的问题，为此采用灵敏度高、体积小的线性TMR传感器替代测量线圈，设计了新的TMR-线圈传感器阵列，对阵列中TMR传感器的敏感轴方向进行了优化，在此基础上选择多维公司TMR2905作为测量器件．结合仿真软件COMSOL Multiphysics和MATLAB，利用模拟扰动法建立了TMR-线圈传感器阵列的灵敏度矩阵．使用Landweber迭代算法求解逆问题，为保证重建图像质量并防止过迭代，设置相邻两次重建结果的剩余测量矢量的差值作为迭代停止条件，通过多次测试选定系统在低固含率和高固含率条件下的迭代阈值分别为0.001和0.050．在仿真和实验平台中针对4种不同的磁导率分布情况进行图形重建，结果表明仿真和实验的重建图像均可以正确反映磁导率在敏感场中的分布信息，验证了TMR-线圈传感器阵列用于测量流化床中磁性催化剂颗粒分布的可行性．为了进一步提高重建图像的质量，通过仿真研究了TMR传感器数量对EMT系统重建图像质量的影响：当TMR传感器从8个增加到16个后，重建图像与实际分布图像的相关系数在4种不同磁导率分布情况下较原来平均提高23.8%．

电磁层析成像；磁性催化剂；隧道磁电阻；传感器阵列设计；图像重建

在一些流化床反应中，使用以铁氧体为内核的磁催化剂可以有效提升反应强度，减少反应副产物[1-2]，同时利于简化反应后催化剂的回收分离过程[3-5]．检测磁性催化剂在流化床内部的分布及运行状态，是流化床优化和设计的重要基础．电磁层析成像技术(electromagnetic tomography，EMT)具有非侵入、实时性等特点，为流化床中磁性催化剂的检测提供了一种有效的解决方案．

自1993年Yu等[6]设计了第1个EMT系统以来，多个EMT系统已被设计和开发，并应用于工业流动测量、医学成像、缺陷检测等领域[7-13]．这些EMT系统均重建电导率分布，且采用线圈检测磁场的设计方案．线圈检测应用了电磁感应原理，因此，测量灵敏度与激励频率、线圈尺寸相关，频率提高，可提高互感灵敏度，会增大容性耦合噪声[14]；线圈尺寸增加，可提高互感电压，但周边放置线圈数目减少，导致独立测量数降低，加大了逆问题求解的欠定性[15].

为了弥补线圈测量的不足，本文使用磁敏感元件(tunneling magneto resistance，TMR)传感器代替检测线圈．磁敏感元件虽然在涡流探伤[16-19]、金属探测[20-22]、角度测量[23-25]等方面已经获得了成功的应用，但在EMT系统中的应用还非常少见．

本文设计了TMR-线圈传感器阵列，优化了TMR敏感轴的放置方向．基于模拟扰动法建立了新型传感器阵列的磁导率灵敏度矩阵，通过Landweber算法获得了磁性催化剂分布的重建图像．

1 EMT磁导率测量理论基础

EMT电磁场分布的数学描述满足麦克斯韦方 程组

 (1)

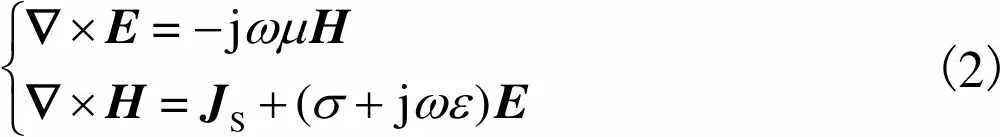
 (2)

本系统采用的激励频率小于1MHz，满足似稳场假设，故可忽略位移电流，将本构方程代入式(2) 可得

 (3)

 (4)

由式(4)可知矢量磁位受物场空间中介质的电导率和磁导率分布的影响，TMR获得的周边磁感应强度值包含了物场内介质磁导率的分布信息，通过求解逆问题可以获得磁导率的分布图像．

2 TMR-线圈传感器阵列设计

2.1 TMR原理

TMR效应产生的原理是自旋相关的隧穿效应. TMR内部的多重隧道结(multiple-tunnel junction，MTJ)结构如图1所示．TMR电阻具有敏感轴测量特性，MTJ中铁磁层(被钉轧层和自由层)和反铁磁层之间的交换耦合作用决定了TMR电阻的敏感轴方向．图1中自由层和被钉轧层的磁矩方向由箭头标出，被钉轧层的磁矩固定，而自由层磁矩可随外界磁场自由旋转．当自由层磁矩与被钉轧层磁矩平行或反向平行时，MTJ分别处于低阻态或高阻态；当自由层磁矩与被钉轧层磁矩垂直时，TMR电阻处于理想工作点[26]，此方向即为TMR电阻测量敏感轴方向．当待测磁感应强度方向与TMR电阻敏感轴方向存在夹角时，TMR电阻测量的是磁感应强度的敏感轴方向分量．

图1 MTJ内部结构

为了获得线性的电压输出，提高测量灵敏度，TMR传感器内部采用4个TMR电阻推挽式全桥结构，如图2所示．1、2、3、4为4个独立的TMR电阻，各自的敏感轴方向如图中箭头所示，TMR传感器的敏感轴方向与1敏感轴方向一致．在外部磁场作用下TMR传感器可产生推挽输出．当电桥工作时，有

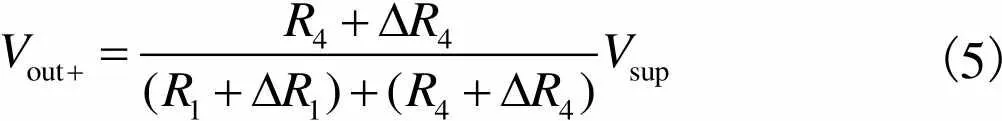
 (5)

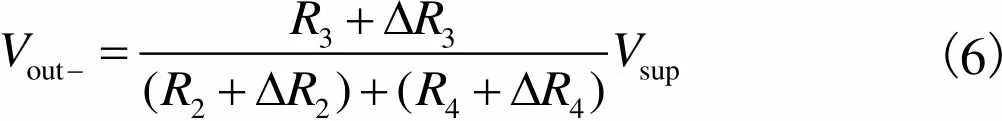
 (6)

当1＝2＝3＝4，Δ1＝Δ3＝－Δ2＝－Δ4时，可得

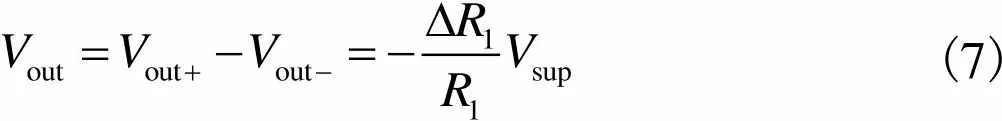
 (7)

2.2 TMR传感器敏感轴方向的选取

由于TMR传感器具有的轴敏感特性，因此，确定适当的敏感轴方向是传感器阵列设计的关键．

TMR-线圈传感器阵列结构如图3所示．待测物场口径为100mm，采用8激励线圈结构，线圈外半径为20mm，内半径为12mm，高度5mm，线径为0.5mm，匝数为160匝．8个TMR传感器放置在线圈轴心位置．

系统采用常规EMT系统的循环激励测量方式．当1号线圈激励时，利用TMR传感器，依次测量2～8位置处的磁感应强度值，然后，切换到2号线圈激励，测量其余位置的磁感应强度，如此循环一周，8次激励共可获得56个测量值．

建立该传感器结构的有限元仿真模型，如图4所示．采用在线圈区域细化剖分的网格剖分策略，线圈和物场区域共剖分8254个域单元、4446个边界单元和1156个边单元用于有限元求解．

由系统的激励测量方式可知，56次测量中，激励线圈和TMR传感器的典型相对位置可分为7类，因此，只考虑2～8号7个位置线圈激励时，1号位置处的磁感应强度与方向，就可代表所有的激励测量位置关系．

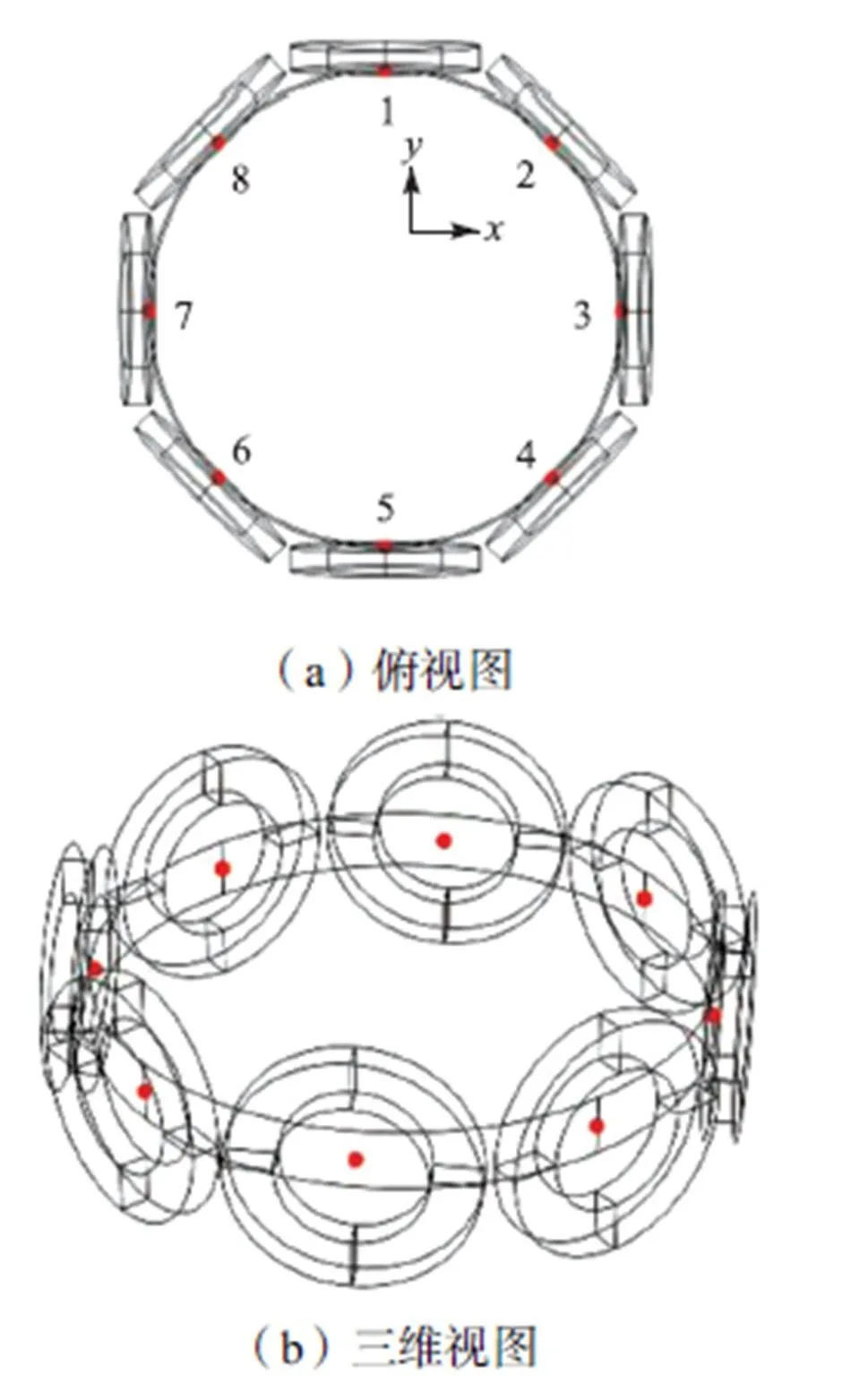
图3 TMR-线圈传感器阵列结构

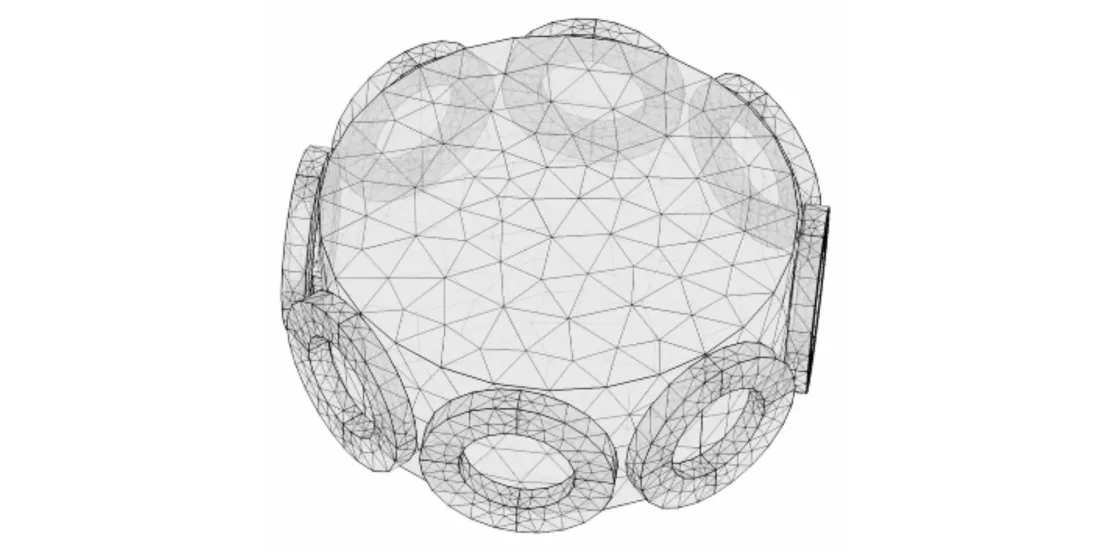
图4 三维EMT模型网格

定义轴与1号激励线圈的轴线重合，如图3(a)中所示．提取1号TMR处磁感应强度的、轴分量，可获得该位置的磁感应强度矢量的方向，如图5所示，当矢量方向相近时，用不同的线型加以区分．不同的线圈激励时，1号位置处磁感应强度矢量与轴的夹角最小达到66.5°．因此使TMR传感器的敏感轴与激励线圈的轴线一致，可兼顾7类激励线圈与TMR传感器器件的相对位置，使各TMR传感器在全局测量中获得较大的磁感应强度测量值．

在选定TMR传感器敏感轴方向的基础上，在仿真模型中计算了成像区域为空气即相对磁导率为1时，使用有效值0.176A、频率1kHz的正弦电流信号激励1号激励线圈时，各测量点的磁感应强度值，如图6所示．磁感应强度范围为16～500mT．根据该范围，选择多维公司TMR2905作为测量器件．

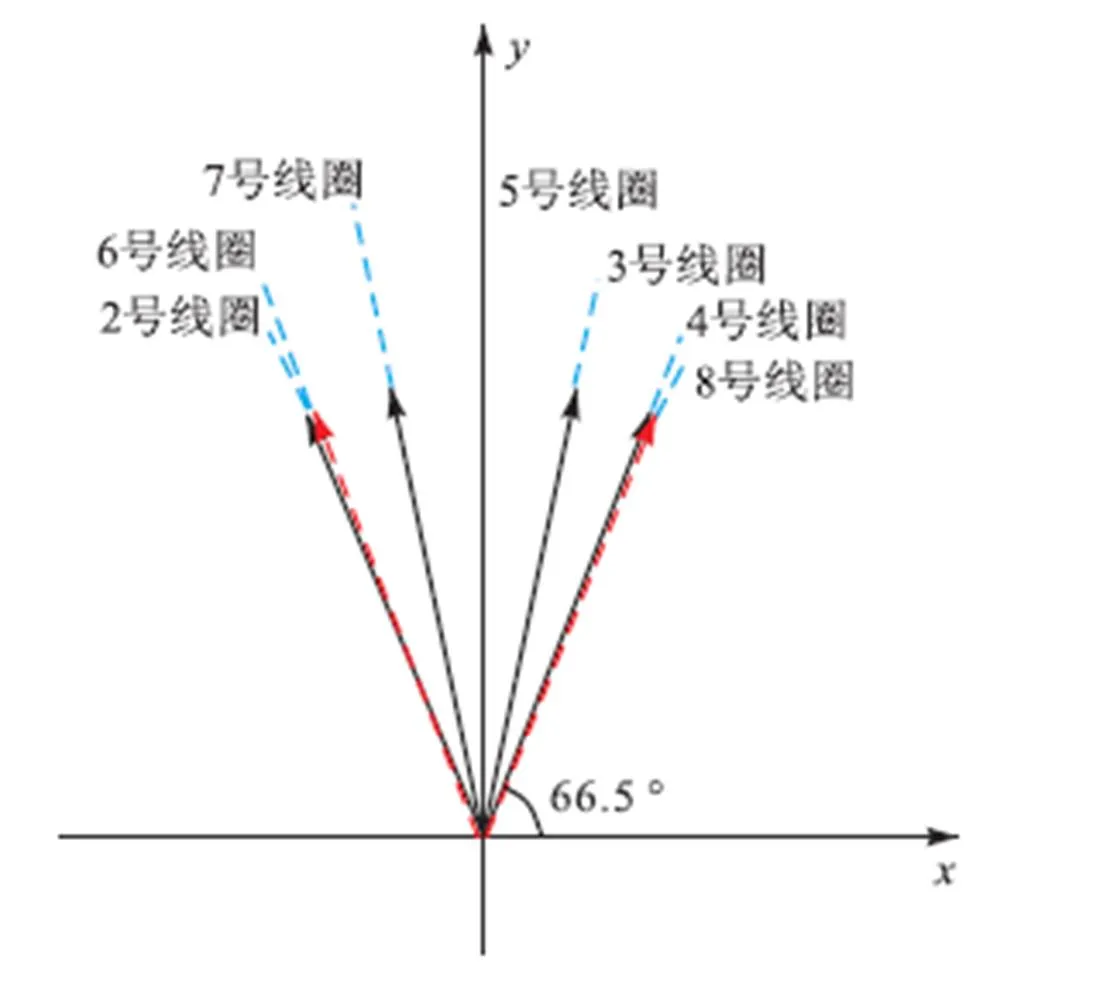
图5 2～8号线圈激励时1号位置处磁感应强度矢量与x轴的夹角

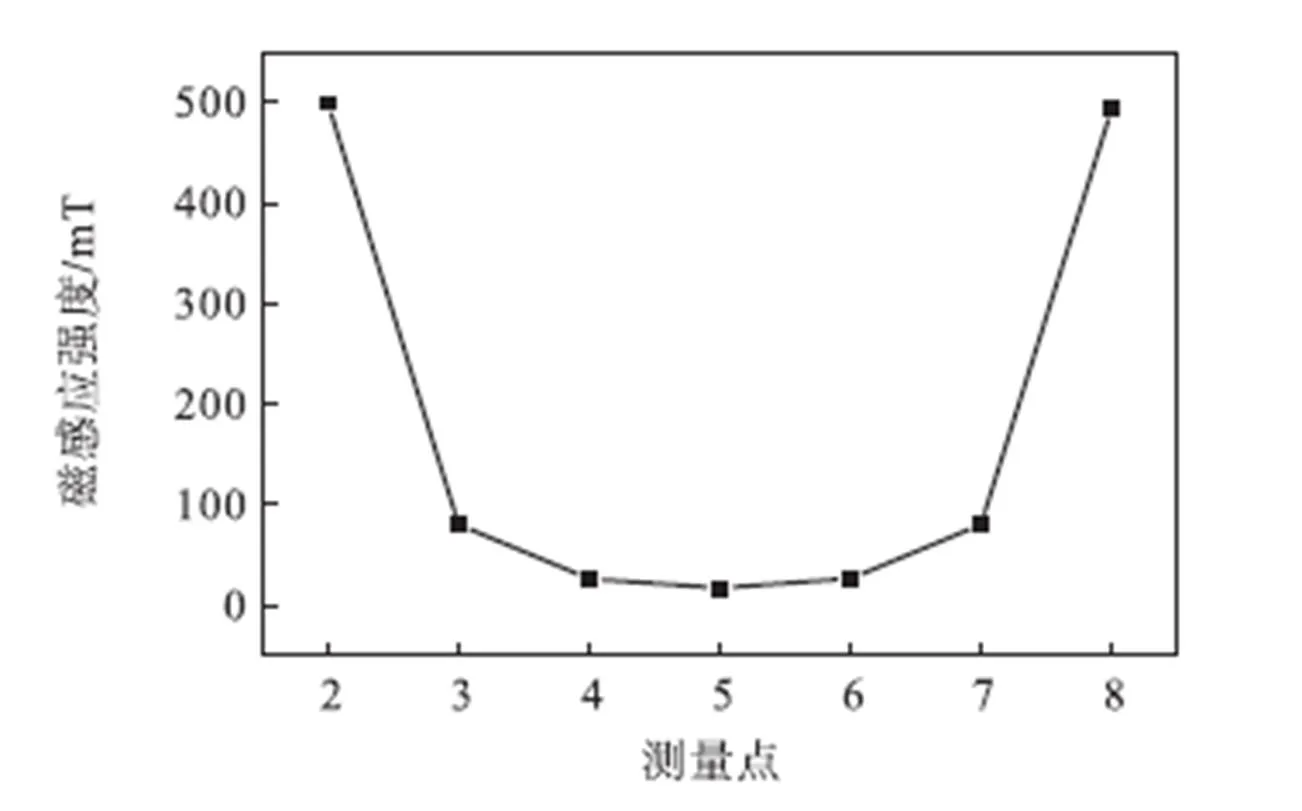
图6 各测量点磁感应强度仿真结果

3 磁导率灵敏度矩阵与逆问题

3.1 磁导率灵敏度矩阵的建立

在小扰动的条件下，磁导率与边界磁感应强度测量值的关系可近似为线性问题

 (8)

本系统由于采用TMR传感器代替常规EMT系统的检测线圈，基于特勒根定理的灵敏度矩阵简便计算方法[27-28]不再适用．本文使用扰动法建立灵敏度矩阵．

为了适应流化床高固含率磁性催化剂监测的需求，采取在高磁导率条件下加入相对磁导率为1的扰动的方式建立灵敏度矩阵，定义灵敏度为

 (9)

1号线圈激励时，2～5号TMR检测的灵敏度分布如图7所示．其灵敏度分布与线圈测量的EMT系统存在明显区别[29]．

3.2 逆问题求解

由式(8)可知逆问题求解可表示为

 (10)

由于的逆矩阵不存在，故使用Landweber算法逼近的广义逆，求解逆问题[30]，定义

 (11)

式中为用于控制收敛速度的增益系数．

Landweber计算的迭代公式为

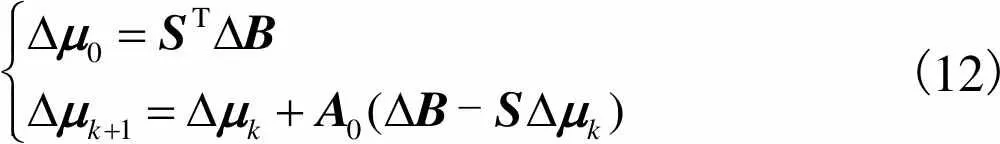
 (12)

为保证迭代过程收敛，需满足

 (13)

当过大时，会导致图像出现过迭代现象；当过小时，会导致成像速度过慢，故一般选取[31]

 (14)

在本文中选取为

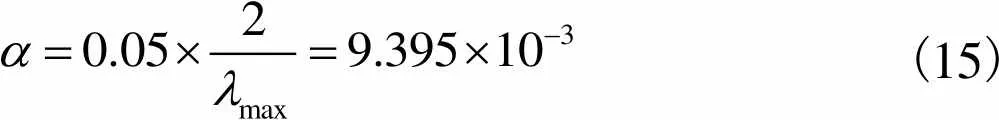
 (15)

定义第次迭代后的剩余测量矢量[31]为

 (16)

为了保证重建图像质量，同时防止图像过迭代，选用相邻两次重建结果的剩余测量矢量的差值作为迭代停止条件[30]．当该差值小于一定阈值时，即认为迭代已收敛至理想的重建结果．经过实验，针对低固含率和高固含率两种情况设置不同的迭代停止阈值

 (17)

4 仿真和实验

4.1 仿真结果

在图4所示EMT三维模型中测取空场与待测物场的边界测量值，利用建立的二维磁导率灵敏度矩阵，对图8中4种不同磁导率分布模型进行图像重建，物场内的圆柱表示待测物体，半径和高度都为10mm，相对磁导率为5，背景相对磁导率为1．结果如图9所示，重建图像色标用于区分磁导率差异，蓝色代表相对磁导率为1，红色代表相对磁导率为5．

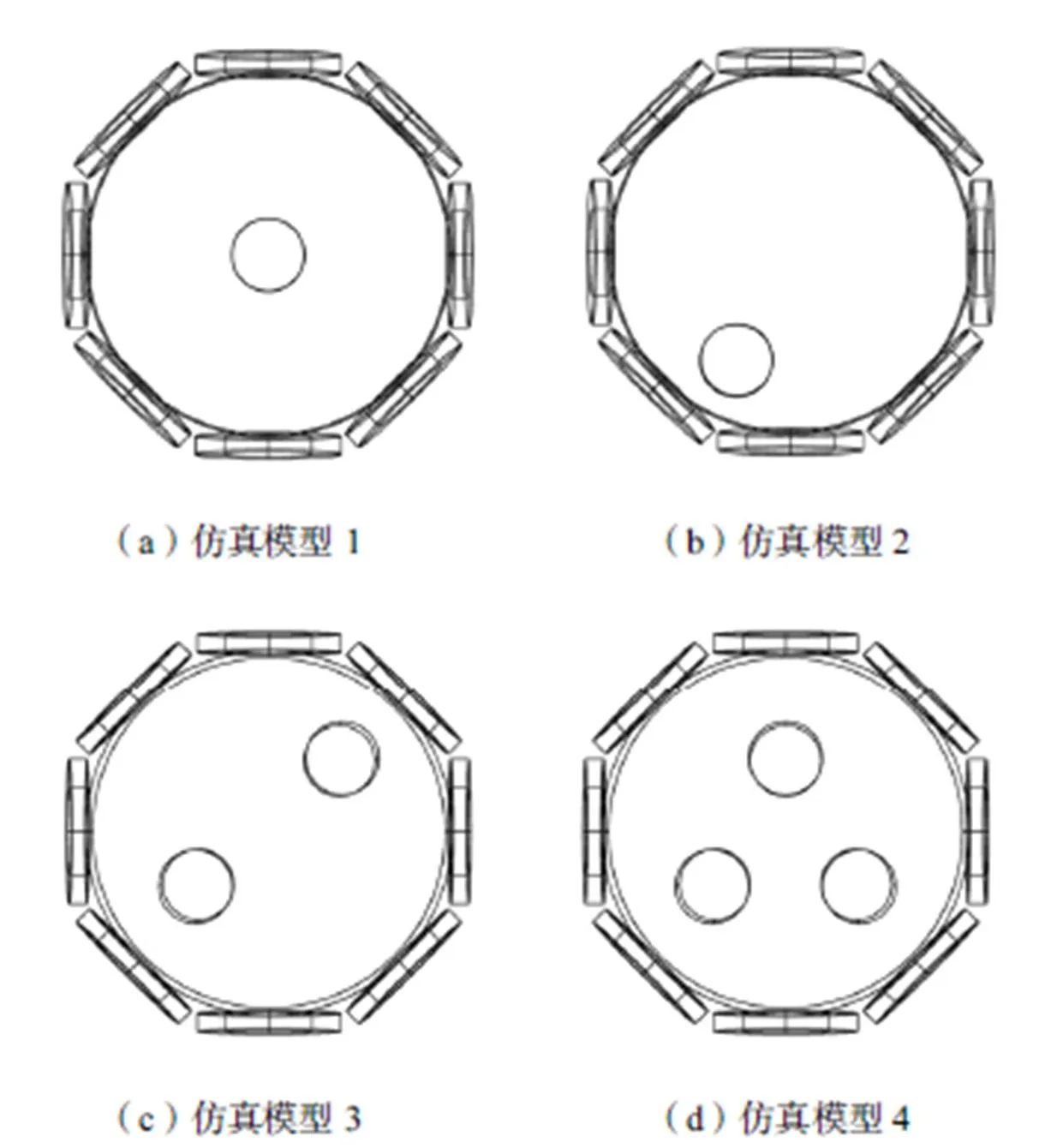
图8 重建模型

从4种不同磁导率分布的图像重建结果观察，重建图像能够正确反映圆柱体待测物体的位置．但当被测物体位于物场中心时，物场边界附近的重建信息失真较为严重；当被测物体距物场边缘较近时，重建物体存在较明显的形状畸变．这可能是由于本文设计的传感器阵列，TMR传感器周围的测量灵敏度远高于物场的中心与其他区域造成的．

图9 图像重建结果

4.2 实验结果

EMT系统的TMR-线圈阵列如图10所示．选用由相对磁导率为180的铁氧体制成的磁屏蔽贴纸作为磁屏蔽层．磁屏蔽层紧贴线圈外围，厚度为0.6mm．系统工作频率为1kHz，激励电流有效值为0.176A．

图10 TMR-线圈传感阵列

在系统平台上设计了不同固含率介质的成像实验．将粒径为0.1mm的铁粉放入直径为20mm和22mm的小瓶中作为待测物体，测试了系统对柱状物体的分辨情况．同时，针对流化床应用需求，进行了高固含率情况下的成像实验．管道为有机玻璃，外径为100mm，管壁厚5mm，使用铁粉和玻璃棒模拟气固两相的分布情况．

系统在不同固含率情况下的成像结果如图11～图14所示(直径为20mm的小瓶标出，其余小瓶直径为22mm)．重建图像可以正确反映出物场内的磁导率物质分布情况，但是还不够精细．本文设计的传感器阵列中只设置了8个TMR传感器，没发挥出TMR传感器尺寸小的优势．增加TMR传感器数量，则增加了系统的独立测量数，有望改善逆问题求解的欠定性问题，提高重建图像质量．

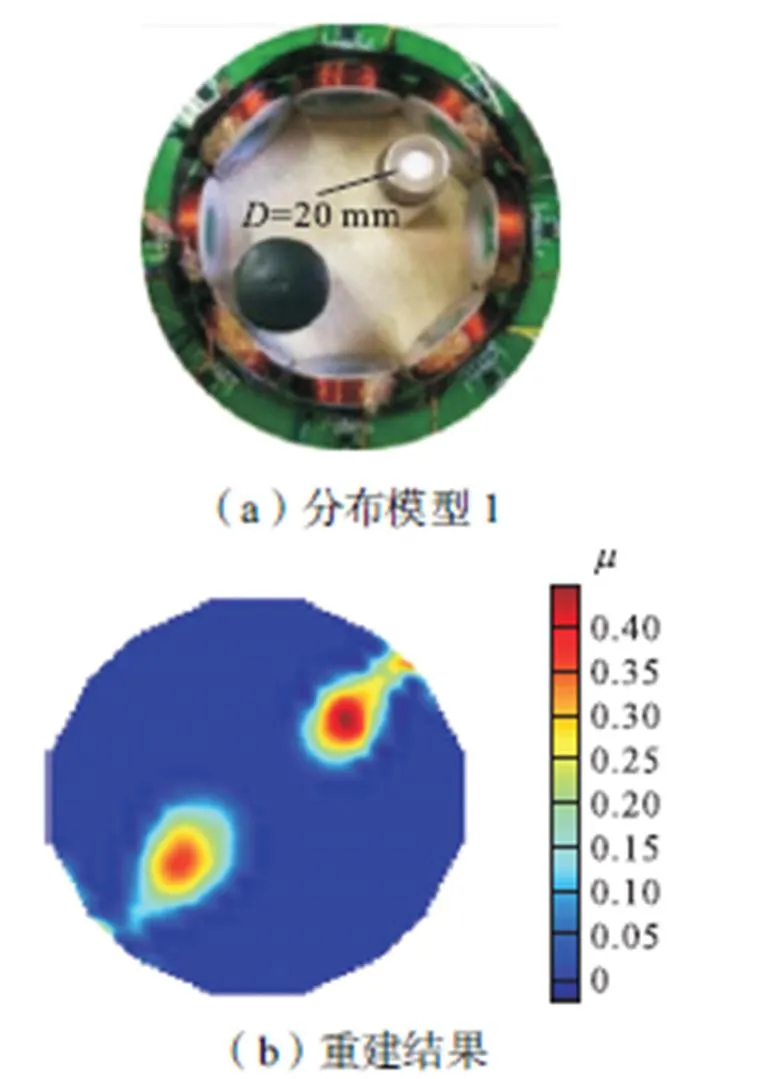
图11 分布模型1成像结果

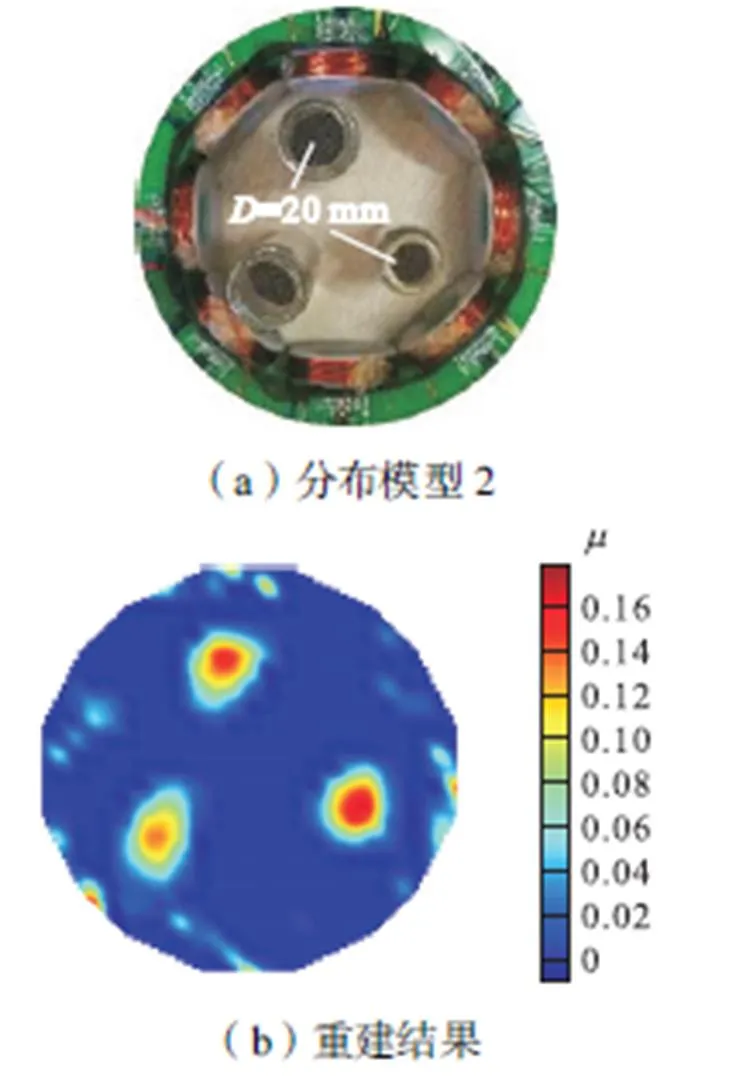
图12 分布模型2成像结果

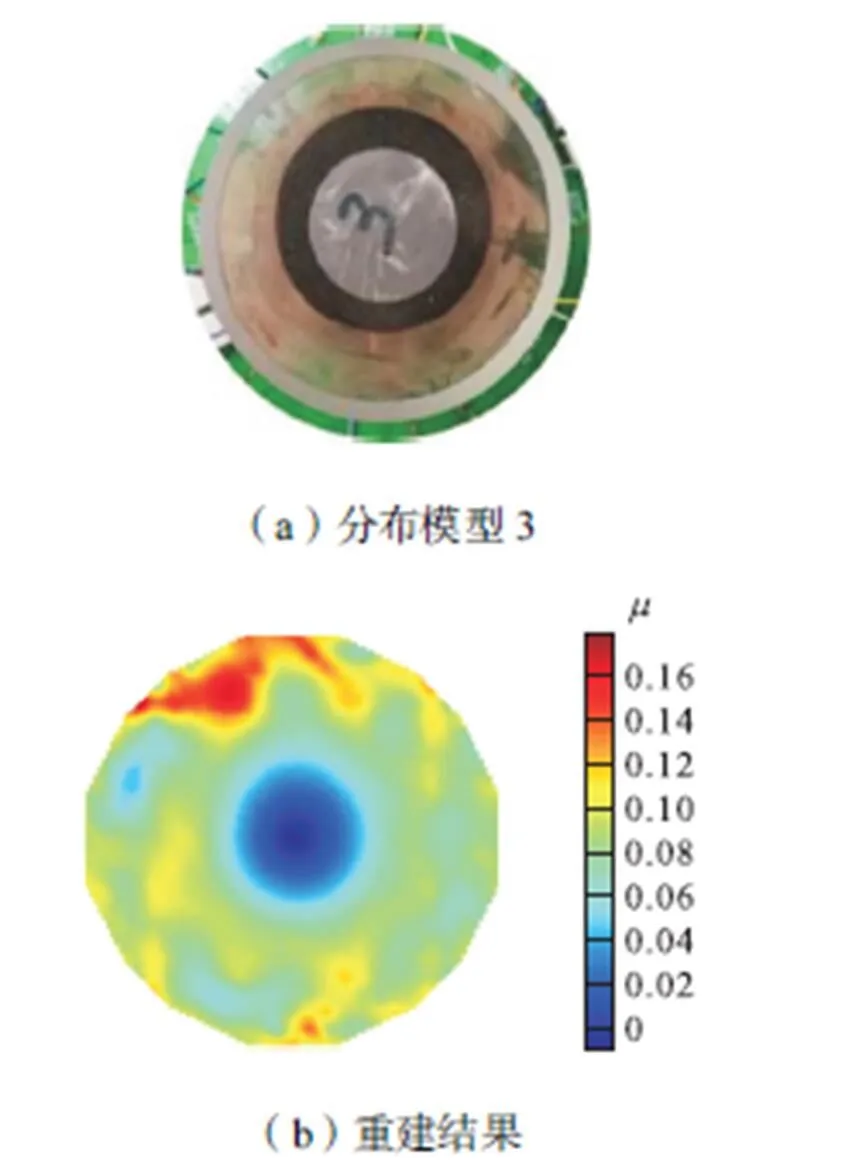
图13 分布模型3成像结果

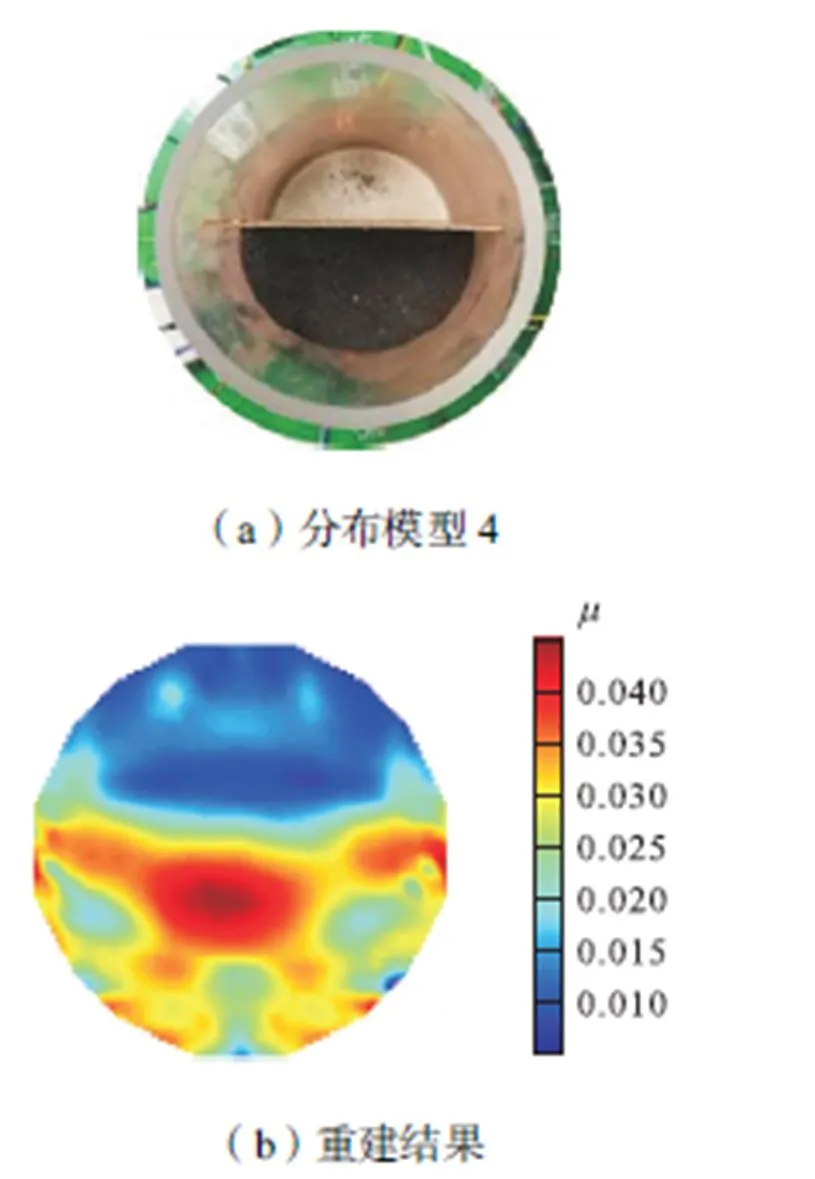
图14 分布模型4成像结果

4.3 增加TMR传感器数量的仿真分析

为了验证增加TMR传感器数量的效果，建立了包括16个TMR传感器和8个激励线圈的传感器阵列，如图15所示．在每次激励过程邻近激励线圈的TMR传感器(位于激励线圈轴心及两侧)输出可能会存在饱和现象．为此，在每一次激励测量过程中只选取除这3个测量点以外的13个TMR上的测量值，即此时EMT系统的独立测量数目为104．同样针对图8所示的4种分布情况下进行了图像重建，结果如图16所示．

与8个TMR传感器情况下的图像重建结果相比较，16个TMR传感器条件下重建图像中被测物质形状更加规则、光滑．当被测物质置于灵敏度较低的中心位置时，物场边界的重建信息的失真得到有效修正；当被测物质位于物场边缘时，被测物质的形状畸变也得到改善．

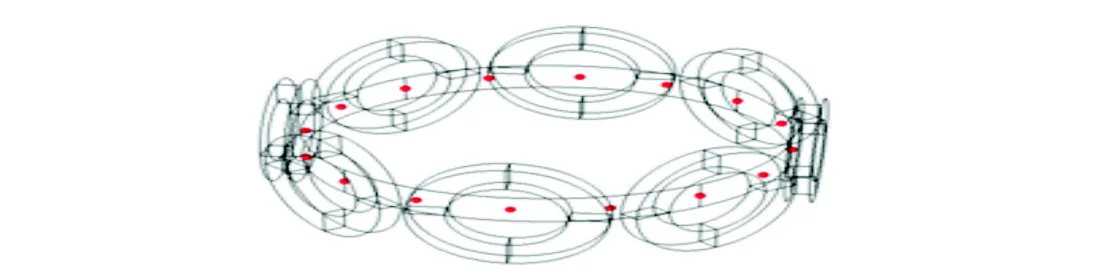
图15 16个TMR-8激励线圈传感器阵列结构

图16 图像重建结果(16个TMR传感器)

为进行定量比较，定义相关系数计算公式[32]为

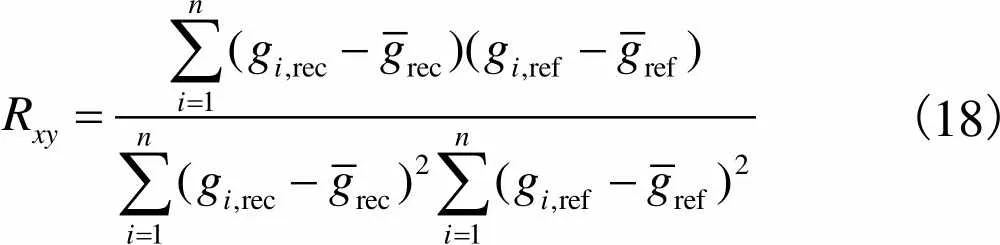
 (18)

表1分别给出了8个和16个TMR传感器的重建图像与实际分布图像的相关系数．从表1结果可知，TMR传感器数目从8个增加到16个后，4种不同分布下的重建图像与实际分布的之间的相关系数平均提高23.8%，即重建的图像更接近于实际分布．

表1 重建图像相关系数

Tab.1 Correlation coefficient of the reconstructed images

5 结 语

本文提出以TMR传感器代替检测线圈，针对TMR传感器的测量特性，设计了TMR-线圈传感器阵列，分析了TMR传感器敏感轴的放置方向．利用二维扰动法计算了新型传感器结构的测量灵敏度矩阵，仿真和实验验证了该传感阵列测量流化床中磁性催化剂分布的可行性．

该方案也可应用于重建电导率分布的EMT系统中．但是，本文设计的EMT系统并未发挥TMR尺寸小，可获得更多测量数据的优势．仿真分析16-TMR的EMT系统与8-TMR的EMT系统相比，重建图像与实际分布图像之间的相关系数平均提高了23.8%．

［1］ Yao G H，Liang H，Gui K T. Physical and chemical effects by magnetic fields for the enhancement of De-NOx by SCR on iron-based catalyst in a fluidized bed[J]. Journal of Engineering Thermophysics，2012，33(9)：1535-1538.

［2］ 熊小龙，刘自力，许翠霞，等. 超顺磁催化剂H3PW12O40/Fe3O4@SiO2的制备、结构表征及在汽油烷基化脱硫中的应用[J]. 化工学报，2014，65(3)： 921-928.

Xiong Xiaolong，Liu Zili，Xu Cuixia，et al. Preparation and characterization of superparamagnetic catalysts H3PW12O40/Fe3O4@SiO2and their application in gasoline alkylation desulfurization[J]. Journal of Chemical Industry，2014，65(3)：921-928(in Chinese).

［3］ Yoon T J，Lee W，Oh Y S，et al. Magnetic nanoparticles as a catalyst vehicle for simple and easy recycling[J]. New Journal of Chemistry，2003，27(2)：227-229.

［4］ 王俊俊，李海涛，马志强，等. 磁性CuO-Bi2O3/ Fe3O4-SiO2-MgO催化剂的制备及甲醛乙炔化性能[J]. 化工学报，2015，66(6)：2098-2104.

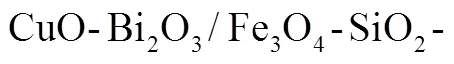
［5］ 王 为，张立静，孟 旭，等. 高饱和磁化强度的Fe3O4磁性颗粒的制备与研究[J]. 天津大学学报:自然科学与工程技术版，2019，52(3)：232-234.

Wang Wei，Zhang Lijing，Meng Xu，et al. Preparation and study of Fe3O4magnetic particles with high saturation magnetization[J]. Journal of Tianjin University：Science and Technology，2019，52(3)：232-234(in Chinese).

［6］ Yu Z Z，Peyton A T，Beck M S，et al. Imaging system based on electromagnetic tomography(EMT)[J]. Electronics Letters，1993，29(7)：625-626.

［7］ Trakic A，Eskandarnia N，Bing Keong L，et al. Rotational magnetic induction tomography[J]. Measurement Science and Technology，2012，23(2)：025402.

［8］ Watson S，Williams R J，Gough W，et al. A magnetic induction tomography system for samples with conductivities below 10 S·m-1[J]. Measurement Science and Technology，2008，19(4)：045501.

［9］ Wang C，Zhang J，Li F，et al. Design of a non-magnetic shielded and integrated electromagnetic tomography system[J]. Measurement Science and Technology，2011，22(10)：104007.

［10］ Vauhkonen M，Hamsch M，Igney C H. A measurement system and image reconstruction in magnetic induction tomography[J]. Physiological Measurement，2008，29(6)：445-454.

［11］ Liu R，Li Y，Fu F，et al. Time-difference imaging of magnetic induction tomography in a three-layer brain physical phantom[J]. Measurement Science and Technology，2014，25(6)：065402.

［12］ Ma X，Peyton A J，Higson S R，et al. Hardware and software design for an electromagnetic induction tomography(EMT)system for high contrast metal process applications[J]. Measurement Science and Technology，2006，17(1)：111-118.

［13］ Lu M，Soleimani M. Hidden defect identification in carbon fibre reinforced polymer plates using magnetic induction tomography[J]. Measurement Science and Technology，2014，25(5)：1009-1016.

［14］ Griffiths N. Magnetic induction tomography[J]. Measurement Science and Technology，2001，12(8)：1126-1131.

［15］ 岳士弘，张洋洋，赵 愉，等. 电学层析成像的灵敏度系数更新算法[J]. 天津大学学报:自然科学与工程技术版，2017，50(12)：5-12.

Yue Shihong，Zhang Yangyang，Zhao Yu，et al. Sensitivity coefficient updating algorithm for electrical tomography[J]. Journal of Tianjin University：Science and Technology，2017，50(12)：5-12(in Chinese).

［16］ Postolache O，Lopes Ribeiro A，Geirinhas Ramos H. GMR array uniform eddy current probe for defect detection in conductive specimens[J]. Measurement，2013，46(10)：4369-4378.

［17］ Dogaru T，Smith C H，Schneider R W，et al. New directions in eddy current sensing[J]. Sensors，2001，18(6)：56-58.

［18］ Gao P，Wang C，Li Y，et al. GMR-based eddy current probe for weld seam inspection and its non-scanning detection study[J]. Nondestructive Testing and Evaluation，2017，32(2)：133-151.

［19］ Wang C，Zhi Y，Gao P. GMR based eddy current system for defect detection[C]//IEEE International Conference on Electronic Measurement and Instruments. Harbin，China，2014：1052-1056.

［20］ Tian G Y，Al-Qubaa A，Wilson J. Design of an electromagnetic imaging system for weapon detection based on GMR sensor arrays[J]. Sensors and Actuators，A：Physical，2012，174(1)：75-84.

［21］ Zhang J，Li D，Kang Y. A novel TMR-based sensor in injected direct current field measurement for nonferrous metal inspection[J]. Studies in Applied Electromagnetics and Mechanics，2017，42：11-18.

［22］ Sakthivel M，George B，Sivaprakasam M. A GMR sensor based guiding tool for location of metal shrapnel during surgery[C]//International Conference on Sensing Technology. Wellington，New Zealand，2014：640-644.

［23］ Bhaskarrao N K，Sreekantan A C，Dutta P K. Analysis of a linearizing direct digitizer with phase-error compensation for TMR angular position sensor[J]. IEEE Transactions on Instrumentation and Measurement，2018，67(8)：1795-1803.

［24］ Granig W，Weinberger M，Reidl C，et al. Integrated GMR angle sensor for electrical commutated motors including features for safety critical applications[J].Pro-cedia Engineering，2010，5：1384-1387.

［25］ Xiao M. A high-accuracy steering wheel angle sensor based on GMR[C]//2016 Sixth International Conference on Instrumentation & Measurement，Computer，Communication and Control(IMCCC). Harbin，China，2016：1-4.

［26］ 张继楷，杨 芸，康宜华，等. TMR传感器及其在电磁检测中的应用[J]. 无损检测，2016，38(12)：36-39.

Zhang Jikai，Yang Yun，Kang Yihua，et al. TMR sensor and its application in electromagnetic detection[J]. Nondestructive Testing，2016，38(12)：36-39(in Chinese).

［27］ Dyck D N，Lowther D A，Freeman E M. A method of computing the sensitivity of electromagnetic quantities to changes in materials and sources[J]. IEEE Transactions on Magnetics，1994，30(5)：3415-3418.

［28］ Yin W，Peyton A J，Stefani F，et al. Theoretical and numerical approaches to the forward problem and sensitivity calculation of a novel contactless inductive flow tomography(CIFT)[J]. Measurement Science and Technology，2009，20(10)：105503.

［29］ 刘 泽，薛芳其，杨国银，等. 电磁层析成像灵敏度矩阵实验测试方法[J]. 仪器仪表学报，2013，34(9)：1982-1988.

Liu Ze，Xue Fangqi，Yang Guoyin，et al. Test method for sensitivity matrix of electromagnetic tomography[J]. Journal of Instrument and Meter，2013，34(9)：1982-1988(in Chinese).

［30］ 王化祥，王 超，陈 磊. 基于Landweber迭代的图像重建算法[J]. 信号处理，2000，16(4)：354-356.

Wang Huaxiang，Wang Chao，Chen Lei. Image reconstruction algorithm based on Landweber iteration[J]. Signal Processing，2000，16(4)：354-356(in Chinese).

［31］ Wang H，Wang C，Yin W. A pre-iteration method for the inverse problem in electrical impedance tomography[J]. IEEE Transactions on Instrumentation and Meas-urement，2004，53(4)：1093-1096.

［32］ Su B，Zhang Y，Peng L，et al. The use of simultaneous iterative reconstruction technique for electrical capacitance tomography[J].Chemical Engineering Jour-nal，2000，77(1)：37-41.

Design of an EMT-TMR Sensor Array for the Measurement of Magnetic Permeability

Wang Chao，Zou Ping，Cui Ziqiang，He Hanchen， Cao Qingqing，Wang Huaxiang

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

To study the real-time monitoring of the magnetic catalyst particles distribution in fluidized beds，the feasibility of applying linear electromagnetic tomography(EMT)technology to the measurement of permeability distribution is studied in this paper. Conventional EMT systems focus on the reconstruction of the conductivity and use measurement coils as detectors，resulting in a low sensitivity of detection and low number of measurements. To solve these problems，tunneling magneto resistance(TMR)sensors are implemented to replace the measurement coils in our system because of their high sensitivity and small size. A novel TMR-coil sensor array has been designed，and the directions of the TMRs’ sensitivity axes have been optimized. On this basis，the TMR2905 of Multi Dimension Corporation is chosen as the measuring device. Using both simulation software COMSOL Multiphysics and MATLAB，the sensitivity matrix of this new array with respect to relative permeability is established according to a perturbation method of simulation. The Landweber iteration algorithm is used to solve the inverse problem in this paper. To ensure the quality of the reconstructed image and prevent over iteration，the difference between the remaining measurement vectors of the two adjacent reconstructed results is set as the stopping condition of the iteration. According to several tests，the iteration thresholds are determined to be 0.001 and 0.050 under low and high solid holdup，respectively. Next，image reconstruction is conducted using both simulation and experiment under four types of permeability distributions. Results show that reconstructed images of both simulation and experiment can correctly reflect the distribution of permeability in the interested field，thereby verifying the feasibility of TMR-coil sensor array’s application in the measurement of magnetic catalyst particles in the fluidized bed. To improve the quality of image reconstruction，the influence of the number of TMR sensors on the quality of the reconstructed image was studied by simulation：when the TMR sensor is increased from 8 to 16，the correlation coefficient between the reconstructed image and the actual distribution increases by an average of 23.8% under four different permeability distributions.

electromagnetic tomography；magnetic catalyst；tunneling magneto resistance(TMR)；sensor array design；image reconstruction

10.11784/tdxbz201806016

TP23

A

0493-2137(2019)06-0559-09

2018-06-08；

2018-11-05.

王 超（1973—），男，博士，教授，wangchao@tju.edu.cn.

崔自强，cuiziqiang@tju.edu.cn.

国家自然科学基金资助项目(61627803)．

the National Natural Science Foundation of China(No.61627803).

(责任编辑：孙立华)