基于PETOOL的大气波导环境下舰艇通信电波传播仿真分析

任 重，李天伟，张海勇

（海军大连舰艇学院，辽宁大连 116018）

0 引 言

大气波导是由低层大气的折射率指数快速减小造成的，由于快速变化的折射率，传播的信号可能会被折射回表面并且陷获在海面和大气波导层之间。相比标准大气，大气波导的陷获效果能在很大程度上使接收的功率增强并且使信号实现超视距传播。因此，大气波导可以作为一种超视距通信的媒介，同时也可以看作是波导信道。大气波导信道的存在，使得海上舰艇不借助中继节点实现超视距大容量高速信息传输成为可能，也带来了舰艇通信电磁隐蔽性、通信盲区等问题，对其进行研究具有重要的理论和应用价值。

对于大气波导信道的研究主要集中在大气波导电波传播方面[1]。抛物方程（Parabolic Equation，PE）方法[2]是波导传播模型中主要采用的技术，这主要是因为PE方法能够支持大气中复杂的边界条件和折射率曲线，同时能够估算路径损耗，这是射线跟踪类方法难以做到的，且用抛物方程法得到的结果经过了实验验证[3]，具有较强的可信性和说服力。基于抛物方程法进行电波传播的预测和计算通常需要借助计算机实现，本文在分析抛物方程模型的基础上，采用首次同时实现单向和双向抛物方程算法的PETOOL 工具，对海上大气波导条件下不同天线高度、不同频率的舰艇通信电波传播情况进行仿真分析，仿真结果可为设计海上大容量超视距通信系统及科学运用舰艇通信系统提供参考依据。

1 大气波导抛物方程传播模型

抛物方程是电磁波波动方程的近似，通常用于计算沿传播方向锥形区域内（近轴方向）的能量传播。Leontovich 等人于20 世纪40年代在处理无线电在地球附近传播的绕射问题时，最早提出了抛物型方程思想[4]。但由于当时的计算条件有限，只能用PE的解析方法计算一些特殊的电波传播问题，因此该思想当时并没有引起太多关注。20 世纪70年代后，随着计算机数值计算方法的发展，抛物方程才重新被提起，目标是进行PE的数值求解。1973年，Hardin 等人在水下声传播问题中提出高效的抛物方程分步傅里叶变换算法[5]，之后PE 方法研究取得了很大进展，在20 世纪80年代开始应用于电磁学领域。目前抛物方程方法及与其他数值算法的组合，已成为大气波导电波传播计算和特性分析的主要方法。

1.1 标准抛物方程

通过引入简化函数u(x,z)=e-ikx ψ(x,z)，由波动方程导出的抛物方程模型在直角坐标系下的表达式为[2]：

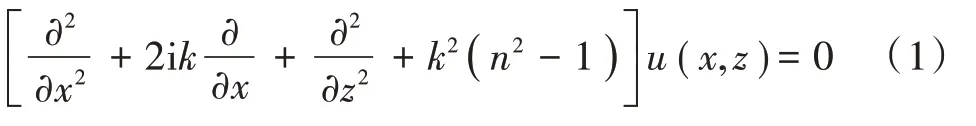
式中：k是真空中的波数；n为大气折射指数；x是电磁波传播距坐标系原点的距离。假设电磁波在大气中向前传播时，大气折射指数n随距离x的变化可忽略不计，则式（1）可分解为：

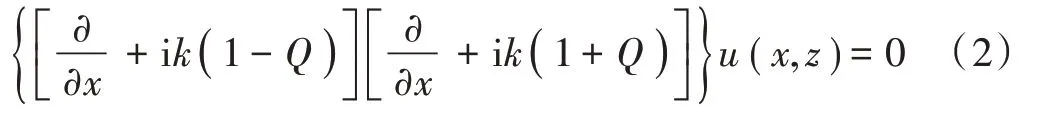
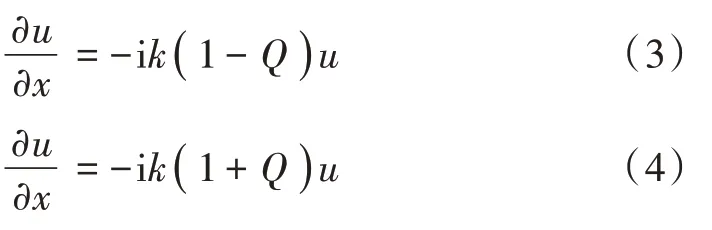
式（3）和式（4）分别对应于前向和后向波传播。若不考虑电磁波后向散射的影响，且仅关注x轴正方向锥形区域内的能量传播时，可利用关于x的一阶伪微分方程求解，则式（3）所示的前向传播抛物方程的通解可表示为：

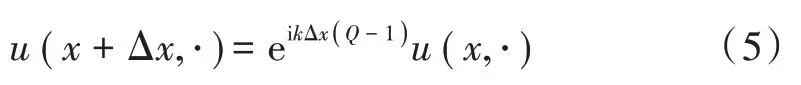
由于伪微分算子Q的存在，式（5）的计算具有一定困难。为此，通常采用一些近似方法来处理，当利用平方根泰勒一阶展开和指数函数时，可得到式（5）的最简单近似，即得到标准抛物方程（SPE）：

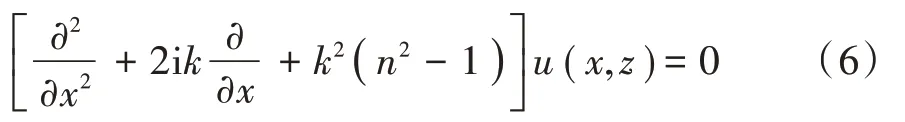
标准抛物方程在计算角度α ＜10°时具有较好的精度，其误差与sin4α成比例。因此，对于传播角度较小的对流层远距离传播计算具有较高的精度，且标准抛物方程可利用分步傅里叶变换方法（SSFT）或有限差分方法（FD）进行数值求解。

而当涉及传播角度较大的问题时，标准抛物方程方法的误差较大，需要对伪微分算子进行更好的近似处理。文献[6]中提出的Claerbout 方程，基于一阶Padé 近似，计算角度可达30°，但其数值求解方法只能采用FD法。FD 法对边界条件的处理较为灵活，但其迭代计算的步长严格受电磁波波长限制，在分析大尺度的电磁波传播问题时，计算时间通常较长；文献[7]提出一种较为有效的Feit-Fleck 近似方法，计算角度范围也可达到30°，并且能够采用SSFT 算法进行快速求解，由于SSFT算法的迭代步长几乎不受电磁波波长限制，且结合快速傅里叶变换（FFT）技术还可实现计算机快速求解，计算效率高、数值稳定性好，因此Feit-Fleck 方法在大尺度电磁波传播领域得到了更广泛的应用。利用该方法可得Feit-Fleck 型宽角抛物方程（WAPE）：

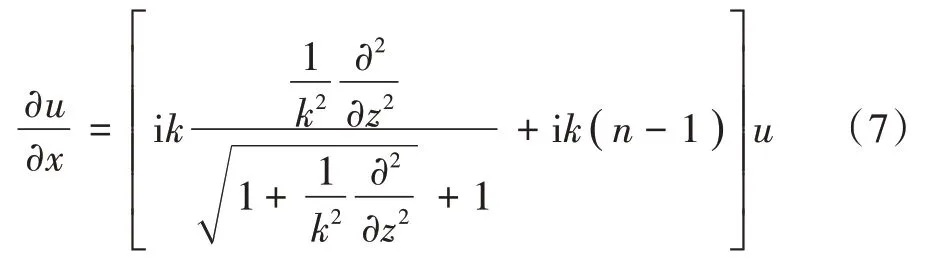
对于式（7）的SSFT 数值计算公式为[8]：

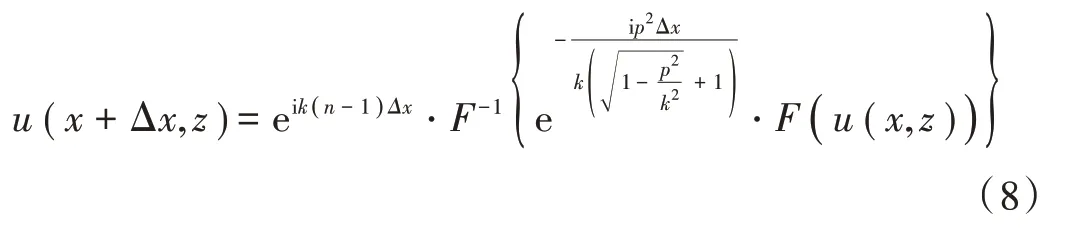
式中：F表示傅里叶变换；p=ksinθ为变换变量（θ为相对于水平方向的传播角度）。

1.2 双向抛物方程

如1.1 节所述，标准抛物方程是一种单向的正向传播模型，因为其忽略了式（4）表示的后向传播项，因此不能反映前向波与后向波之间的相互作用，特别是沿传播路径有陡峭的障碍物时的情况。在存在这些障碍物的情况下，不仅需要考虑前向传播，还应当考虑后向反射、折射和衍射波的影响，才能得到较可靠的结果，为此需要采用双向抛物方程方法。

双向抛物方程方法[9]基本上是单向抛物方程的迭代实现，通过简单地切换传播方向来估计多次反射效应。该算法通过使用阶梯近似，使其适用于不同的地形。如果电磁波遇到障碍物，则它被分成沿前、后两个方向传播的两个分量。前向场分布的计算，在遇到垂直地形面时设置为零，之后以常规方式继续。对于前向传播，利用式（8）在传播方向上不断推进进行数值求解；而对于由障碍物引起的波的后向传播，在双向抛物方程算法中以如下方式实现：首先通过在面上施加边界条件来获得反向场的初始场，然后基于这个初始场，通过反转式（8）中k和Δx的符号，从而在-x方向上推进，进行数值求解。因此，在x-Δx处的后向垂直场分布为：

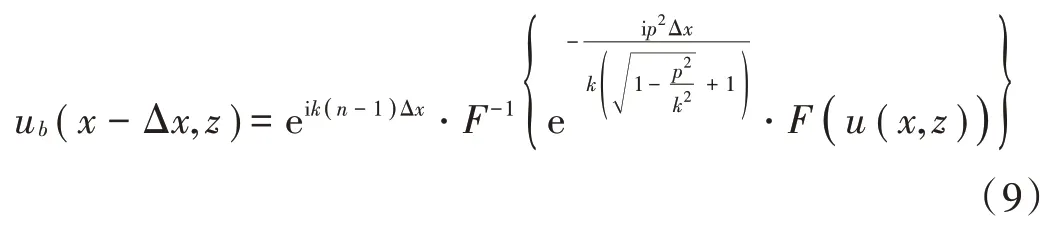
观察可知，式（9）与式（8）具有相同形式，但应注意此时的原始场已变为e-ikxub(x,z)。如此，在电磁波每次遇到障碍物时，被分成前向和后向分量，然后在每个步进计算点处叠加前向场和后向场来获得总的场分布。

2 PETOOL电波传播仿真工具

目前以抛物方程法为基础，已经出现了多种电波传播预测软件[10]。其中，最著名的当属由美军空间战和海战系统中心研发的AREPS（Advanced Refractive Effects Prediction System）[11]。该软件采用射线光学模型和抛物方程法相结合的混合模型，能够根据不同数据源获取的数据计算得到大气折射率，但遗憾的是，该软件的最新版本已不对非美军方人员开放。PETOOL（Parabolic Equation Toolbox，抛物方程工具箱）是由土耳其中东技术大学Ozgun 等人基于Matlab 开发的用于电波传播分析和可视化的软件。PETOOL 同样适用于大气波导环境下的电波传播计算，该工具基于单向和双向分步抛物方程数值算法，具有友好的图形用户界面（GUI），支持在不同地形、均匀和非均匀的大气条件下，对电磁波的前向和后向传播进行建模分析和显示。其主界面如图1所示，主要包括参数设置区、地形可视化编辑区和结果显示区。该软件具有大气折射率廓线自定义、地形自定义、按高度/范围的路径损耗分析等功能，支持数据保存及加载、仿真结果图生成等操作。本文采用PETOOL 工具对海上大气波导条件下的舰艇通信电波传播影响因素进行仿真研究，主要考虑以下几方面因素：

1）PETOOL 是开源的电波传播计算仿真工具。由于可以自由地查看和修改算法实现代码，能够确认软件实现的有效性，且支持后续自行对算法和软件进行改进完善及验证。

2）PETOOL 是可靠的电波传播计算仿真工具。PETOOL仿真计算的结果与AREPS 进行对比验证[12]，能够获得与AREPS 相当的结果。

3）PETOOL 是首个实现前后双向递归分步抛物方程算法的软件包[12]。相比于AREPS，PETOOL 还考虑了后向传播的电磁波，使得PETOOL 在分析收发双方间存在岛屿、舰船等障碍物时的精度更高。

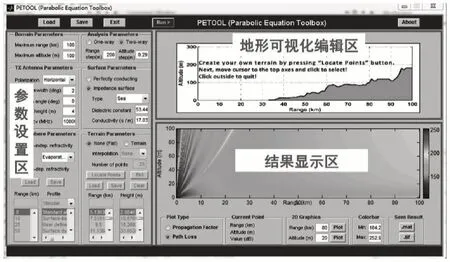
图1 PETOOL软件主界面Fig.1 Main interface of PETOOL software

3 大气波导环境下舰艇通信电波传播仿真分析

3.1 接收天线高度对电波传播影响仿真分析

在大气波导环境下，舰艇超短波微波通信效果会因天线高度不同而受到影响。本节以表面波导为例，对不同接收天线高度时的电波传播路径损耗进行仿真分析。主要参数设置如表1 所示。

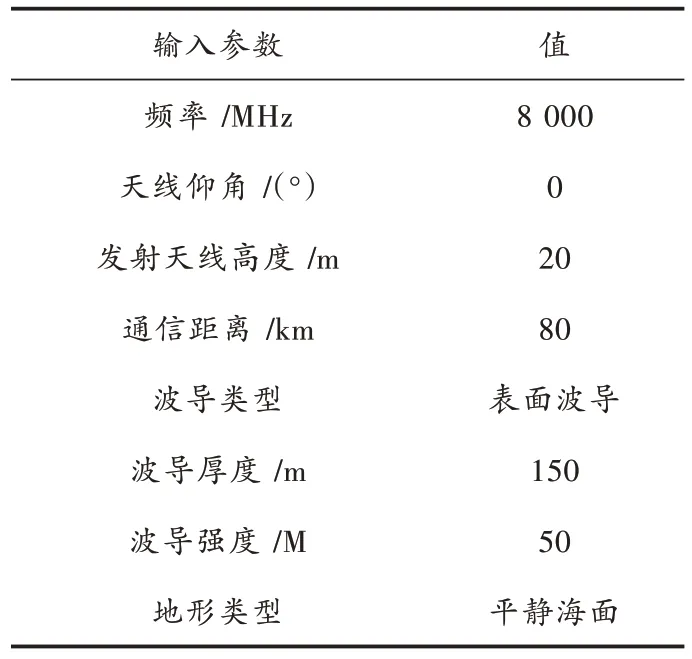
表1 主要参数设置Table 1 Setting of main parameters

仿真得到路径损耗情况如图2 所示。由仿真结果可见：接收天线高度低于100 m时，路径损耗较小；大于100 m时，损耗值迅速增大。因此，若通信双方位置距离预先能够确定，可根据传播路径损耗最低值优化接收天线高度，达到最佳通信效果。

3.2 通信频率对电波传播影响仿真分析

考虑舰艇超短波通信频段和数据链、卫星通信使用的微波频段，选取频点进行仿真（主要参数与3.1 节设置一致），仿真结果如图3 所示。

可见微波频段电波受陷获较强，随着频率的升高，顶部盲区变大，处于微波频段的舰艇数据链通信和低仰角时的卫星通信需要注意电磁隐蔽及通信盲区问题。

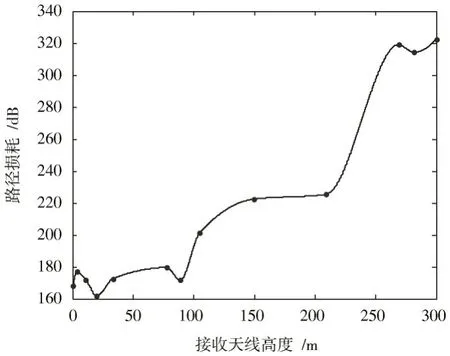
图2 不同接收天线高度的电波传播路径损耗Fig.2 Path loss of radio propagation at different heights of receiving antenna

图3 不同频率条件下的电波传播路径损耗Fig.3 Path loss of radio propagation at different frequencies

4 结 语

对大气波导环境下电波传播特性的研究是分析如何实现舰艇超短波微波超视距通信，合理利用或规避通信盲区，提高电磁隐蔽性等问题的关键支撑，而传播特性研究的关键是对大气波导传播进行建模并进行模型求解和仿真预测。本文针对此关键点，按照从窄角到宽角、从单向到双向的逻辑，分析了抛物方程模型及其分步傅里叶变换数值求解方法，选择采用首次同时实现单向和双向抛物方程算法的PETOOL 工具，对海上大气波导条件下不同接收天线高度、不同频率的舰艇通信电波传播情况进行仿真分析，得到了具有一定参考价值的仿真结果。然而，也应注意到PETOOL的功能仍然较为单一，如蒸发波导大气折射率模型较为简单、粗糙，海面传播环境仿真支持不足等，还可进一步对算法进行研究完善；此外，将PETOOL 中路径损耗预测计算与通信系统收发模型、海上复杂电磁环境相结合，构建更加贴近实际的通信距离预测模型，也是值得进一步研究的重要方向。