基于神经网络的桩基承载力预测
路 利 民
(河北工程大学土木工程学院,河北 邯郸 056038)
桩基由于对环境影响小、质量可靠等多方面的优点,近年来在工程中得到了迅速推广。桩的极限承载力是工程人员关注的重要性能指标之一。目前,现场载荷实验可以准确测定单桩的极限承载力,但是该实验费用高,时间长,试桩数量有限。因此,寻找一种简单高效的方法来预测桩基承载力意义重大。
目前众多学者将神经网络应用于桩基承载力预测并取得了一些有益的成果[1,2]。然而,由于土体性质的复杂性,影响桩基承载力的因素很多,各因素所占的比重也是随时间、空间等多种因素的不断变化而变化的。过多的参数固然可以更加准确的反映桩基承载力和各因素间的关系,但不可避免的是,参数过多将造成神经网络结构复杂。
主成分分析法是一种多变量统计方法,其目的在于对原始数据进行降维,用较少的几个综合指标(即主成分)来代表原始数据。因此本文利用主成分分析法和径向基神经网络两者的优势,对桩基进行承载力预测。
1 主成分分析法
主成分分析法也就是主分量分析法,它利用降维思想,将各种指标转化为信息损失较小的多个综合指标,每个主成分都是原始变量的线性组合。而且各主成分不相关,这使得主成分相比原始变量有更加优越的性能,从而提高分析效率。主成分分析法的主要步骤为:
1)原始数据归一化。
数据归一化目的是为了消除数据量纲不同、数量级相差较大而引起的差异。常见的归一化方法为:
应用上述方法,将所使用到的数据A变换到[0.1,0.9]区间内,得到矩阵Bm×n。
2)求解协方差矩阵。按照式(1)对矩阵B进行标准化处理,得到标准化矩阵C=(cjk)。
(1)
式中:
然后计算标准化矩阵C的协方差矩阵,并求其特征值。
3)根据上一步所求的特征值从大到小排列,按照式(2)计算各特征值贡献率p。
(2)
4)求解主成分。利用式(3)求解各主成分。
E=B×D
(3)
其中,D为各特征值对应的特征向量。
2 径向基神经网络(RBF)
神经网络是一个复杂的网络系统,可以将其理解为一个“黑盒子”,它包括大量简单的处理单元,这些处理单元通过特定的方式相互连接,形成了一个可以模仿人脑结构和功能的系统。径向基神经网络是由Love和Bromhead依据径向基函数可以在多维空间进行插值这一特性而提出的一种全新的神经网络。
相对于经典的BP神经网络收敛速度慢,容易陷入局部极小值的缺点,RBF神经网络学习时间短,计算量小,局部逼近性能优良等特点,使其得到了广泛应用。径向基网络结构如图1所示。
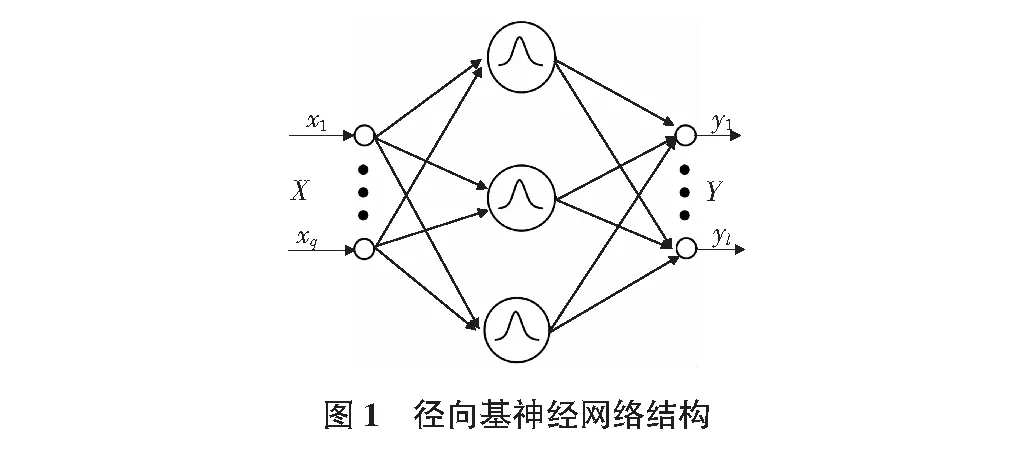
径向基神经网络有3个网络层:输入层,径向基层(隐层)和线性层(输出层)。输入层用于输入信息。
3 计算结果
本文使用MATLAB中的newrbe函数设计径向基函数网络,其基本格式为:net=newrbe(P,T,SPREAD)。
其中,P为输入量;T为目标量;SPREAD为分布密度。SPREAD的不同取值,将会影响网络的预测精度,因此需要选取不同的值对网络进行训练,并且依据预测结果和实测结果来最终确定SPREAD的取值。本文取工程数据[3]前22组数据进行拟合,后6组数据进行预测。通过对SPREAD取不同的值,观察其对网络性能的影响。计算表明,当取0.41时,预测结果和实测结果吻合较好。预测值和实测值见表1。
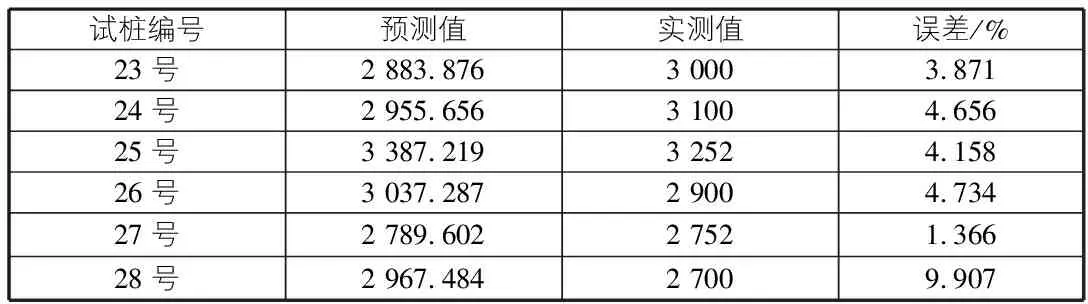
表1 预测值和实测值
4 结语
本文应用MATLAB软件计算参数SPREAD的取值,在计算速度提高的同时,可以取得更加精确的参数值。从预测结果中可以看出,大多数预测值误差在5%之内,最大误差不超过10%,在工程中,这一误差是可以接受的。

