长周期地震动参数拟合研究

于建杰 赵 艺

(东北林业大学土木工程学院，黑龙江 哈尔滨 150000)

随着我国经济的发展，超高层建筑，隔震建筑及大跨度桥梁等长周期结构的出现，这些结构在长周期地震动作用下容易发生共振进而引发倒塌，同时我国规范并未给出针对长周期结构抗震设计的相应规定，对长周期设计反应谱的研究日益迫切。

1 长周期地震动的选取

1999年9月21日凌晨1时47分，我国台湾南投县集集地区发生7.6级大地震，震源10 km左右，断层距小于20 km，为典型的近断层地震动，这场地震为研究近场地震提供了大量的强震记录。本文研究用到的记录皆是从太平洋地震工程研究中心(PEER)所下载。李雪红等[1]对大量地震动的时域，频谱分布，地震动放大系数及周期特性进行了分析，提出了用β谱曲线2 s～10 s谱值的平方加权平均值β1进行判断，当β1>0.4时即为长周期地震动。根据这一标准，并考虑到剔除微小地震动影响，本文基于如下三个标准对长周期地震动进行了选择。

1)震中距R<100 km;2)峰值速度PGV>5 cm/s;3)峰值加速度PGA>0.04g;4)β1>0.4。

2 观察记录分组

根据郝敏、谢礼立等[2]的研究，集集地震的震中烈度为10度。周锡元等[3]通过对我国大量地震动的统计，给出了考虑震中距和震级的烈度评定方法，如式(1)所示：

I0=0.24+1.26M

I=0.92+1.63M-3.49lgR

(1)

其中,I0为震中烈度;I为基本烈度;M为地震震级;R为震中距。

集集地震的震级是7.62级，由式(1)可以计算出震中烈度为9.84。这与郝敏、谢礼立等人的研究非常吻合。

本文从美国太平洋地震工程研究官网(PEER)下载了地震动，包含了丰富的地震动信息包括震级和震中距，但是各地震动台站所属的地区烈度并未给出。耿淑伟等[4]提出，在缺乏烈度资料时，可以采用震级和震中距来计算烈度，通过与震中烈度相比来划分设计地震分组，具体情况如表1所示。

表1 远、近震界定与地震分组对照表

吕红山等[5]通过对中关两国场地分类指标进行了对比和对场地土层波速测试资料的分析，给出了中国的场地类型划分与地表30 m等效剪切波速V30的对应关系，对应关系如表2所示。

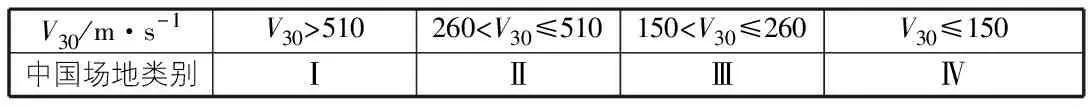
表2 中国场地类别与V30对应关系

根据场地类别和地震分组，对所收集到的长周期地震动进行了分组，如表3所示。

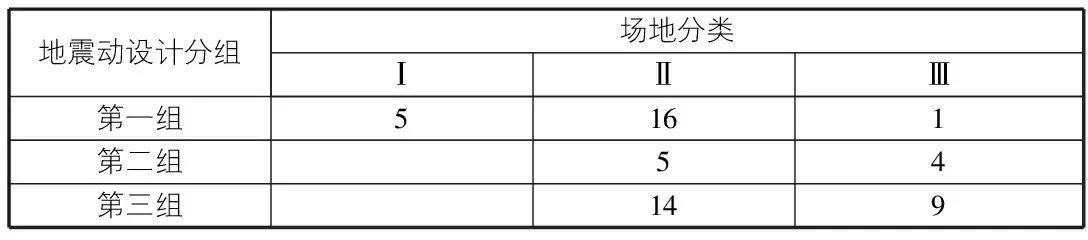
表3 场地类别与对应分组

3 反应谱原理

设计反应谱模型最早出现在20世纪60年代末期，Newmark等人提出了三参数模型，其原理表述如下：根据共振原理，反应谱的长周期，中长周期和短周期，分别受位移，速度和加速度控制，并假设各类谱平直段的放大系数分别为：

Ka=Sa0/a；Kv=Sv0/v；Kd=Sd0/d

(2)

其中，Sa0,Sv0和Sd0分别为加速度反应谱高频段、速度谱中频段和位移谱的反应谱低频段的均值；a,v和d分别为地震动峰值加速度、峰值速度和峰值位移。又根据拟谱关系，Sa0,Sv0和Sd0之间有如下近似关系，即：

Sa0=ωSv0=ω2Sd0

(3)

由于Newmark提出的该模型物理意义明确，我国现行的基于地震影响系数和特征周期的设计反应谱也是由此演变而来。

设计反应谱的确定是根据大量地震动观测数据为基础的，取相同或相近的条件下大量地震动记录，在一定的阻尼比情况下，经过规准化、平均化和平滑化这三个程序得到设计反应谱。

对于一条给定的地震动记录，在拟合反应谱时需要遵循一定规律来保证拟合精度，主要有以下三条原则：

1)最小二乘法。2)反应谱在拐点处连续。3)面积相等原则。根据这一原则可以建立等式关系，减少一个参数，从而提高拟合的精度和质量。

4 遗传算法理论

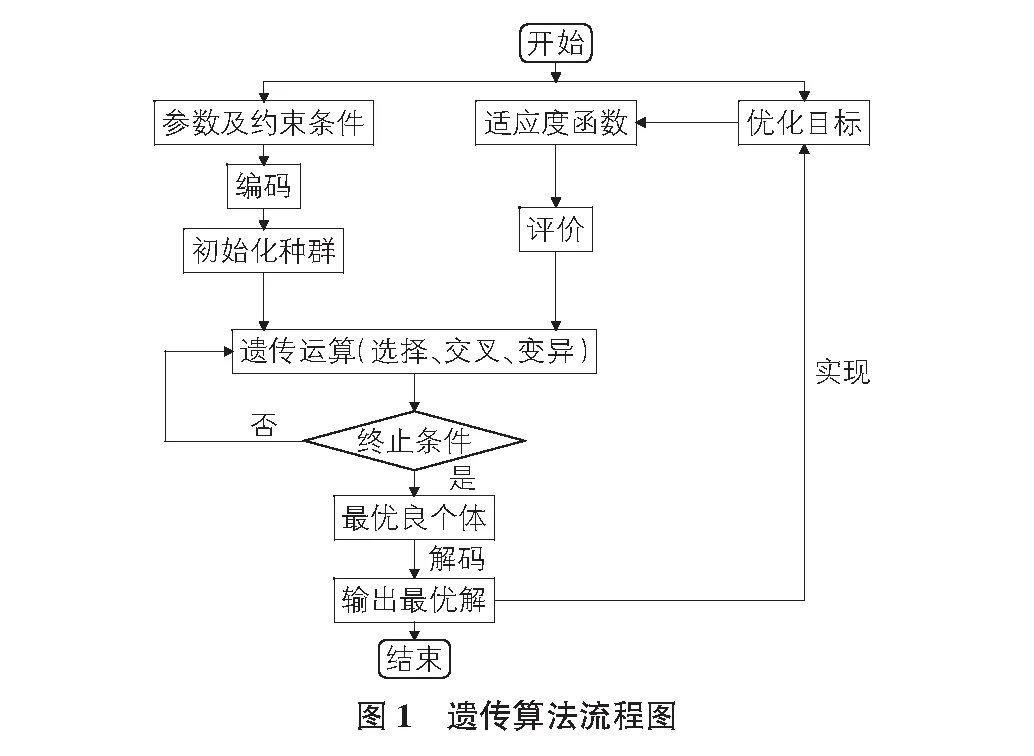
遗传算法(Genetic Algorithm，简称GA)是根据自然界中遗传、突变、杂交和自然选择等现象发展而来的用于最优解问题的搜索算法，它是一种高效自适应的方法，使用者通过，选择算子，交叉算子和变异算子等遗传操作及边界条件来控制具体的优化过程，最终通过终止条件结束算法。遗传算法有启发式算法，爬山法，穷举法和盲目随机法等传统优化算法。

传算法具有以下的优点：

1)对可行解表示的广泛性。

2)群体搜索特性。

3)不需要辅助信息。

4)内在启发式随机搜索特性。

遗传算法具体的流程图如图1所示。

5 常规设计反应谱对长周期地震动的拟合

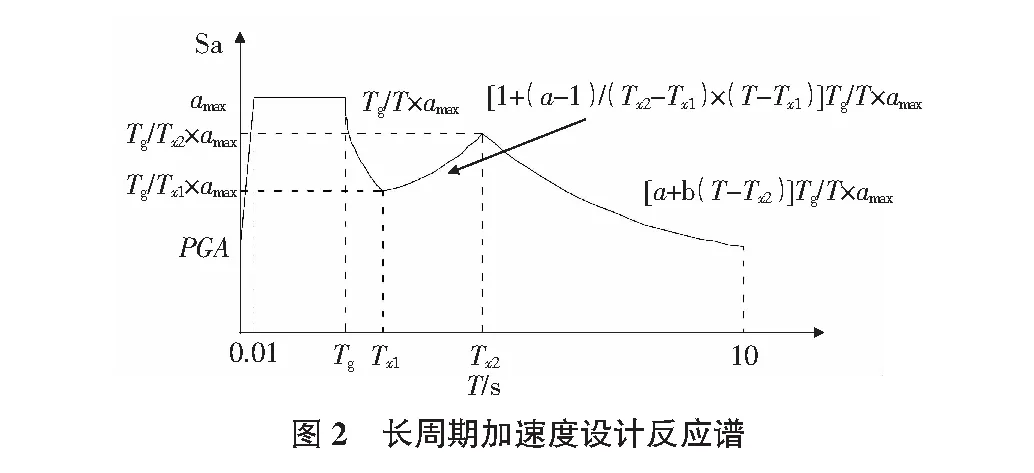
在对长周期结构进行长周期地震动输入的时候，反应谱长周期段显得格外重要，但目前我国现行规范对大于6 s的长周期部分未给出具体规定。邱立珊[6]给出了其根据速度反应谱和拟谱公式(式(3))给出的长周期地震动加速度反应谱如图2所示。由图2可知待优化的参数为αmax,Tg,Tx1,Tx2,a和b共6个参数。其形状可以较好地反映长周期加速度反应谱在长周期部分幅值较大的特点。由于参数较多，而遗传算法可以对多参数问题进行优化，故可以使用遗传算法来进行参数的确定。

6 结语

长周期设计反应谱不同于现行规范给出的设计反应谱，其典型的特征为长周期部分幅值较大，下降规律与常规设计反应谱有明显不同。由于长周期设计反应谱所涉及参数较多，遗传算法是解决这一问题的良好方法。至于在不同分组下的取值有待于进一步研究。