具有时延和切换拓扑的高阶离散时间多智能体系统鲁棒保性能一致性

徐君 张国良 曾静 孙巧 羊帆,4

近年来,多智能体系统的分布式协调控制问题受到了研究者的极大关注,在卫星编队[1−2]、多无人系统[3−4]、无线传感器网络[5−6]等实际系统都有广泛应用.一致性问题作为多智能体系统分布式协调控制的一个基础问题,一经提出就得到研究者的普遍重视[7−12],它要求每个智能体仅利用自身和邻居的状态信息,通过设计合适的一致性协议,使得多智能体系统的某个感兴趣的状态变量相同或趋于一致.解决一致性问题的基本框架最早由Olfati-Saber等在文献[7]提出,主要研究多智能体系统的一阶一致性问题.Ren等在文献[8]考虑了二阶多智能体系统的一致性问题,给出了二阶多智能体系统获得一致性的充分条件.文献[9]考虑了邻域交互结构优化的二阶多智能体快速蜂拥控制算法.Xi等在文献[10]提出高阶连续时间多智能体系统的一致性问题,并将高阶多智能体系统的模型描述为一般线性系统.文献[11]研究了一类控制器模态和系统模态不匹配的异步切换高阶多智能体系统的输出调节一致性问题.文献[12]研究了时延和切换拓扑条件下高阶离散时间多智能体系统的一致性问题.文献[13]讨论了有领导者条件下高阶离散时间多智能体系统的一致性问题.随着研究的深入,研究者发现之前的研究仅考虑了系统的稳定性,没有考虑系统的性能指标,例如系统的能量消耗.基于此考虑,Cheng等在文献[14]中提出了保性能一致性问题.保性能一致性的优点在于它不仅考虑了多智能体系统的一致性稳定性,还考虑了多智能体系统的能量消耗.实际的多智能体系统所携带的能量往往都是有限的,因此研究多智能体系统的保性能一致性问题具有十分重要的工程意义.文献[15]和文献[16]研究了连续时间多智能体系统的一阶保性能一致性问题.文献[17]研究了连续时间多智能体系统的二阶保性能一致性问题.上述文献研究的是连续时间多智能体系统的保性能一致性问题,且没有考虑系统的鲁棒性.Xu等在文献[18]中考虑了高阶离散时间多智能体系统的鲁棒保性能一致性问题.但是,文献[18]仅仅讨论了固定拓扑和无时延条件下的高阶离散时间多智能体系统的鲁棒保性能一致性问题,没有涉及时延和切换拓扑的情况.受此启发,本文考虑研究时延和联合连通切换拓扑条件下的高阶离散时间多智能体系统的鲁棒保性能一致性问题.

本文符号说明如下:1N表示维数为N的元素全为1的列向量;I表示适当维数的单位矩阵;rank表示矩阵的秩;⊗表示Kronecker直积[17];∗表示对称矩阵的中的相应对称元素.

1 图论知识

用G=(V,E,A)表示一个有向图,其中,V={v1,···,vN}表示图的N个节点集;E⊆V×V表示图的边集,节点序号属于一个固定的节点序列集I={1,2,···,N},图G的边用eij=(vi,vj)表示,eij表示从vi到vj的信息流,vi称做父节点,vj称做子节点.用非负矩阵A=[aij]表示其邻接矩阵,图G的边eij关联的权重aij非负.另外假定aii=0,i∈I.如果eij∈E⇔eji∈E,则称图G为一个无向图.图G的Laplacian矩阵定义为L(G)=L=∆−A,其中为图G的度矩阵.ei是第i个元素为1其余元素为0的列向量.

2 问题描述

文献[10]指出,高阶多智能体系统一致性问题可以用一般线性群系统一致性问题描述.因此,本文考虑一个由N个同构智能体组成的高阶离散时间不确定线性多智能体系统.

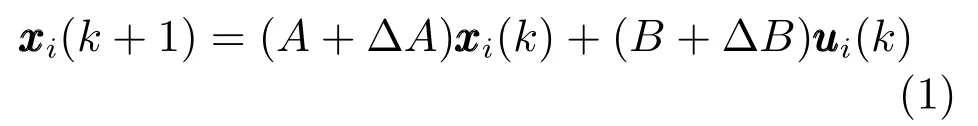
其中,i=1,2,···,N,xi(k)∈Rd和ui(k)∈Rm分别表示智能体i的系统状态和控制向量,A和B是适当维数的常数矩阵,且(A,B)可控.∆A和∆B是适当维数的不确定矩阵,假定形式如下:

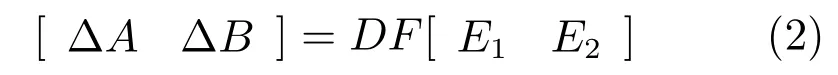
其中,D,E1和E2是合适维数的常数矩阵,反映了离散时间多智能体系统(1)中的每一个智能体的不确定性结构,F是一个满足

的未知矩阵,且可以是时变的.

注 1.在实际多智能体系统中,由于系统器件老化等原因,系统的参数常常会发生变化,但一般不会太大,因此本文做出式(3)的假设.另外,∆A和∆B在实际系统中也不完全一定始终满足∆A=DFE1和∆B=DFE2,如果∆1或∆2,高阶离散时间不确定多智能体系统(1)的鲁棒保性能问题将变得十分复杂,本文不做讨论.

假定高阶离散时间不确定多智能体系统(1)在k时刻的通信拓扑为Gσ(k),并用ΓN={Gσ(k)}表示通信拓扑Gσ(k)所有可能拓扑结构的集合,具体表示为

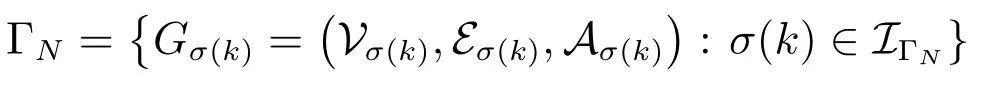
其中,IΓN={1,2,···,M},σ(k):[0,∞)→IΓN表示通信拓扑的切换信号,即通信拓扑集ΓN中元素的索引.Lσ(k)=L(Gσ(k))为系统在k时刻通信拓扑Gσ(k)的Laplacian矩阵.

针对高阶离散时间不确定多智能体系(1)的一致性问题,本文采用如下线性一致性协议:

其中,K是合适维的常值反馈矩阵,τ(k)是变时延,且满足0≤τ(k)≤τmax,τmax为最大允许时延,aij(σ(k))表示当切换信号为σ(k)时,智能体j到智能体i的作用权重.

令δij(k)=xi(k)− xj(k),定义保性能函数

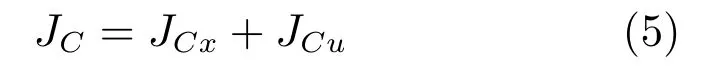
其中,

其中,Qx和Qu为给定的对称正定加权矩阵.

定义1.对于高阶离散时间不确定多智能体系统(1),如果存在一个序列c(k)和一个正数使得成立,则称不确定多智能体系统(1)达到保性能一致性,c(k)称做一致性序列,称做保性能代价.

注2.JC是一个与高阶离散时间不确定多智能体系统(1)参数相关的保性能函数,其中,JCu描述了系统控制输入的能量消耗,JCx描述了一致性协议(4)造成的能量消耗,保性能一致性的实质就是寻找一个JCu和JCx之间的平衡,具体就是寻找一个合适的反馈增益矩阵K使得保性能函数JC存在一个上界.由此可以看出,保性能一致性本质上是从能量优化的角度考虑了多智能体系统的一致性,但最优解一般很难得到,一般求出次优解即可.

3 保性能一致性协议设计

其中,ϕ(k)=0.为了分析联合连通条件下高阶离散时间多智能体闭环系统(6)的一致性问题.

引理1[19].用L表示一个无向图G的Laplacian矩阵,则零是它的一个特征值,如果G连通,则零是L的单一特征值,并且L的其他所有特征值均为正实数.

定义 2.设存在一个有限时间段[k0,k0+κ),使得切换通信拓扑Gσ(k)在[k0,k0+κ)时间段内的联合作用通信拓扑Gκ是连通的,则称切换通信拓扑Gσ(k)在有限时间段[k0,k0+κ)联合连通.其中表示Gσ(k)在[k0,k0+κ)时间段内的并集,所对应的邻接矩阵Aκ和Laplacian矩阵Lκ分别满足.

注3.联合连通与一般意义的切换拓扑的区别是联合连通的子拓扑不一定是连通的,而一般意义的切换拓扑的每个子拓扑都是连通的,这样多智能体系统在联合连通条件下的一致性问题将更加复杂.

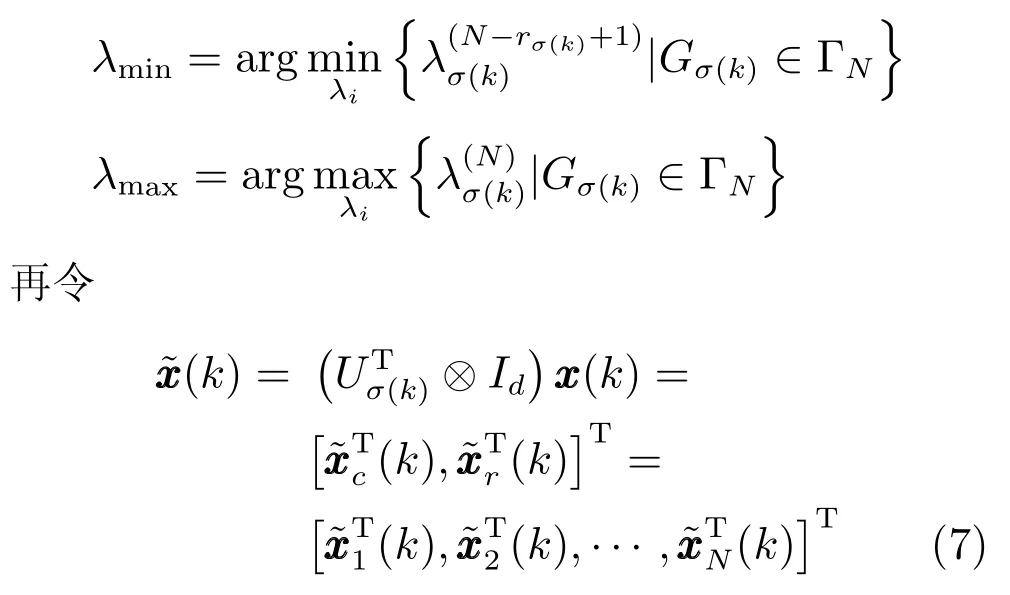
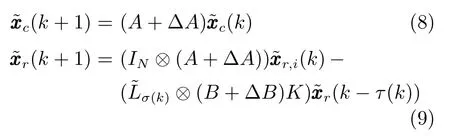
显然,如果子系统(9)Schur稳定,则闭环多智能体系统(6)获得一致性.需要说明的是,这个条件与文献[10]中的高阶连续时间多智能体系统情况类似,区别是对于高阶连续时间多智能体系统,子系统(9)需要的是Hurwitz稳定.

另外,保性能函数(5)可写为

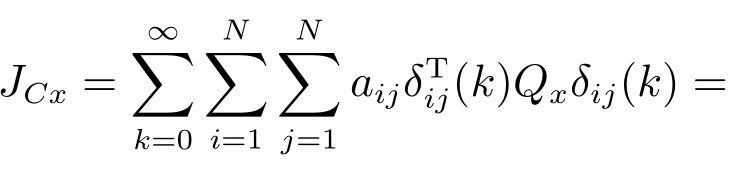
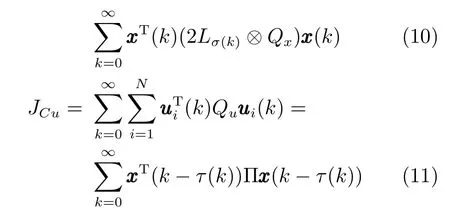
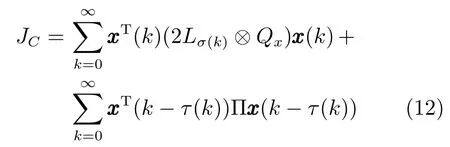
引理2(Jensen不等式)[20].对于任意常值矩阵M≥0,M∈Rn×n,ψ(i)∈Rn,正整数α1,α2,且α2≥α1≥1,如下不等式成立:

引理3.考虑一个高阶离散时间不确定多智能体系统(1),同时假定它的通信作用拓扑是联合连通的,时间延迟为τ(k).如果存在合适维的矩阵K,d×d维的矩阵R1,R2,Q1,Q2满足

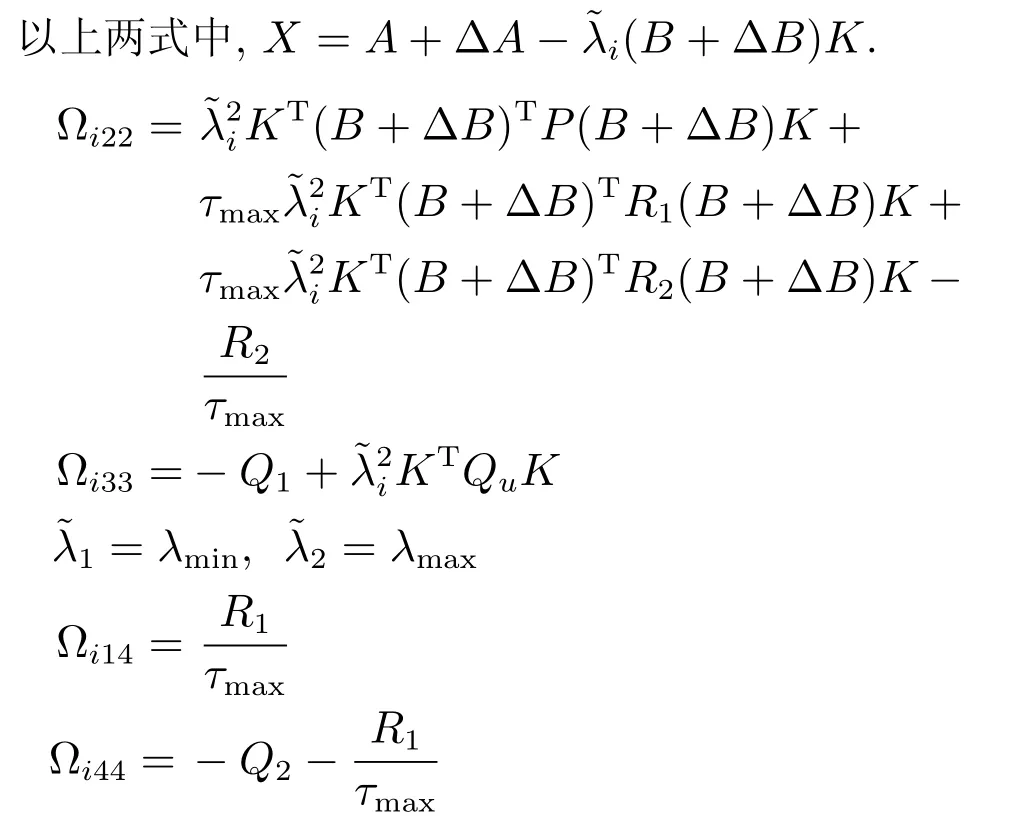
则高阶离散时间不确定多智能体系统(1)能在一致性协议(4)作用下获得保性能一致性,且它的保性能函数上界满足

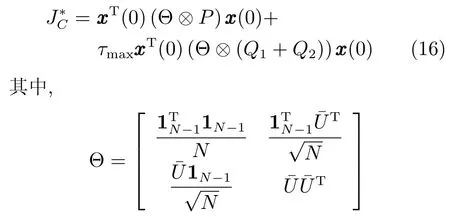
证明.考虑Lyapunov函数候选

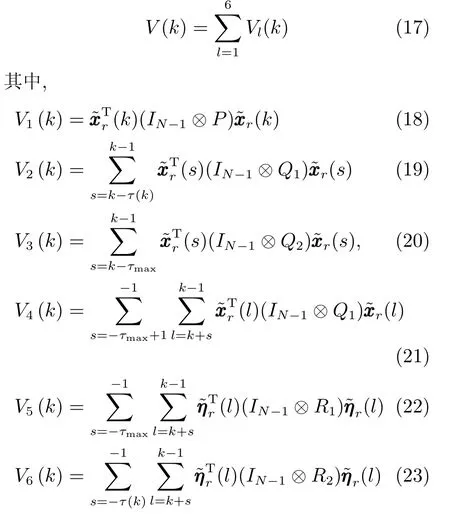
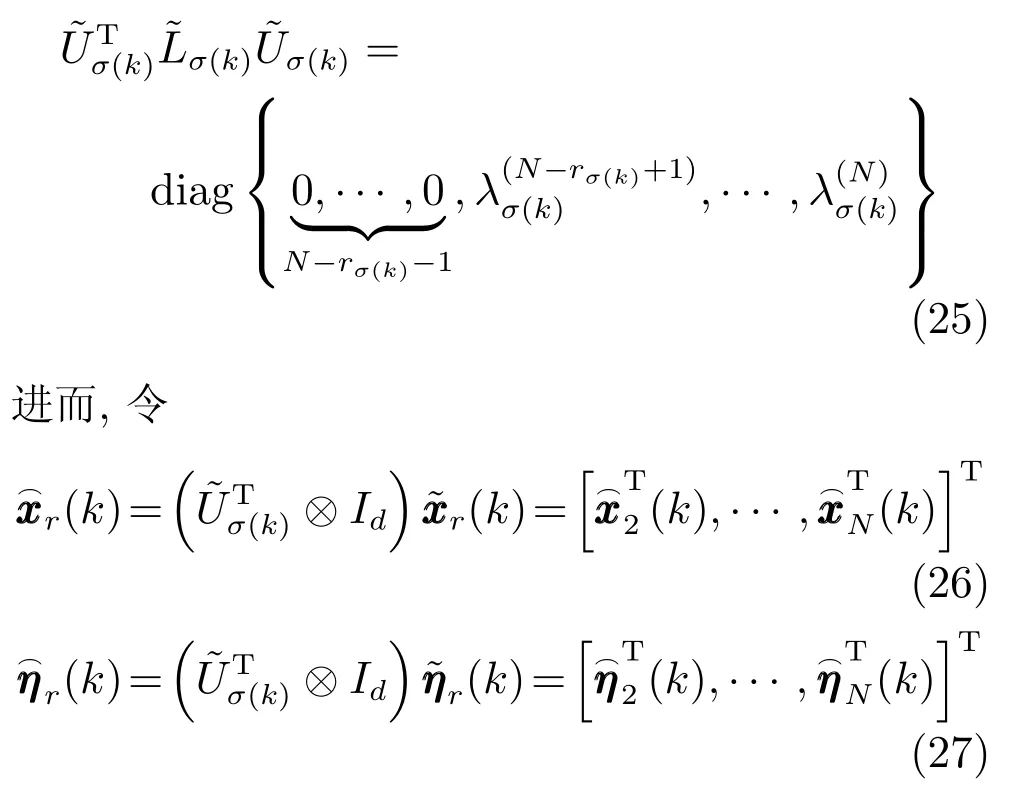
将式(25)和(26)代入式(24)可得,∆V1(k)沿着式(6)的差分为

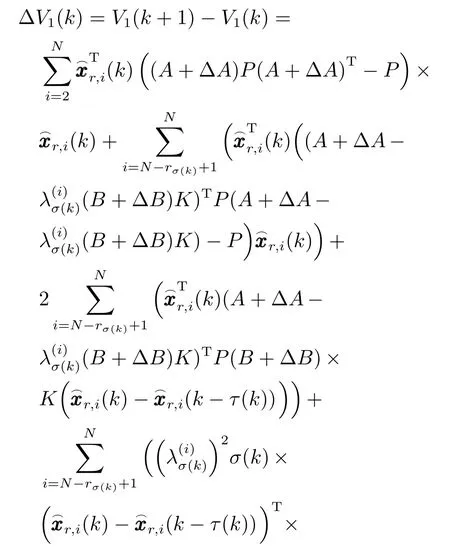
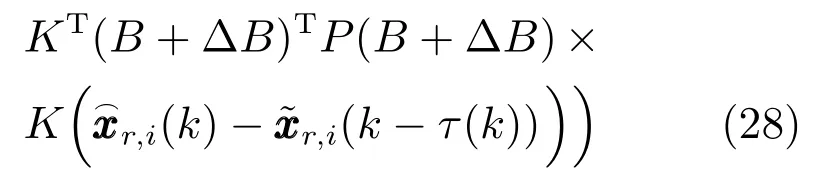
∆V2(k)沿着式(6)的差分为

∆V3(k)沿着式(6)的差分为

∆V4(k)沿着式(6)的差分为

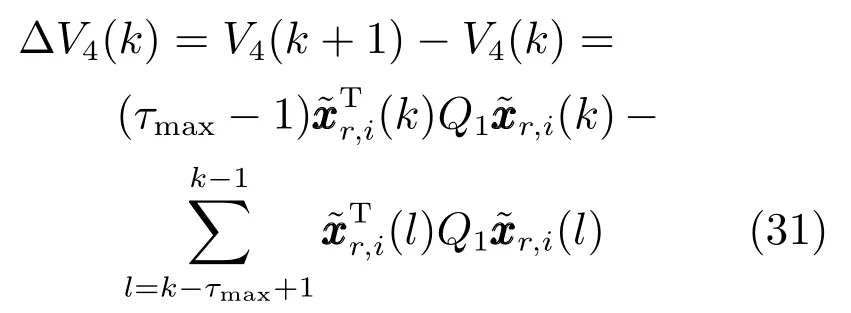
∆V5(k)沿着式(6)的差分为

同时,根据引理2,可得

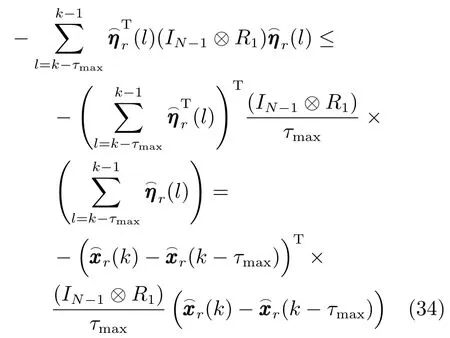
∆V6(k)沿着式(6)的差分为

进一步,做出如下定义

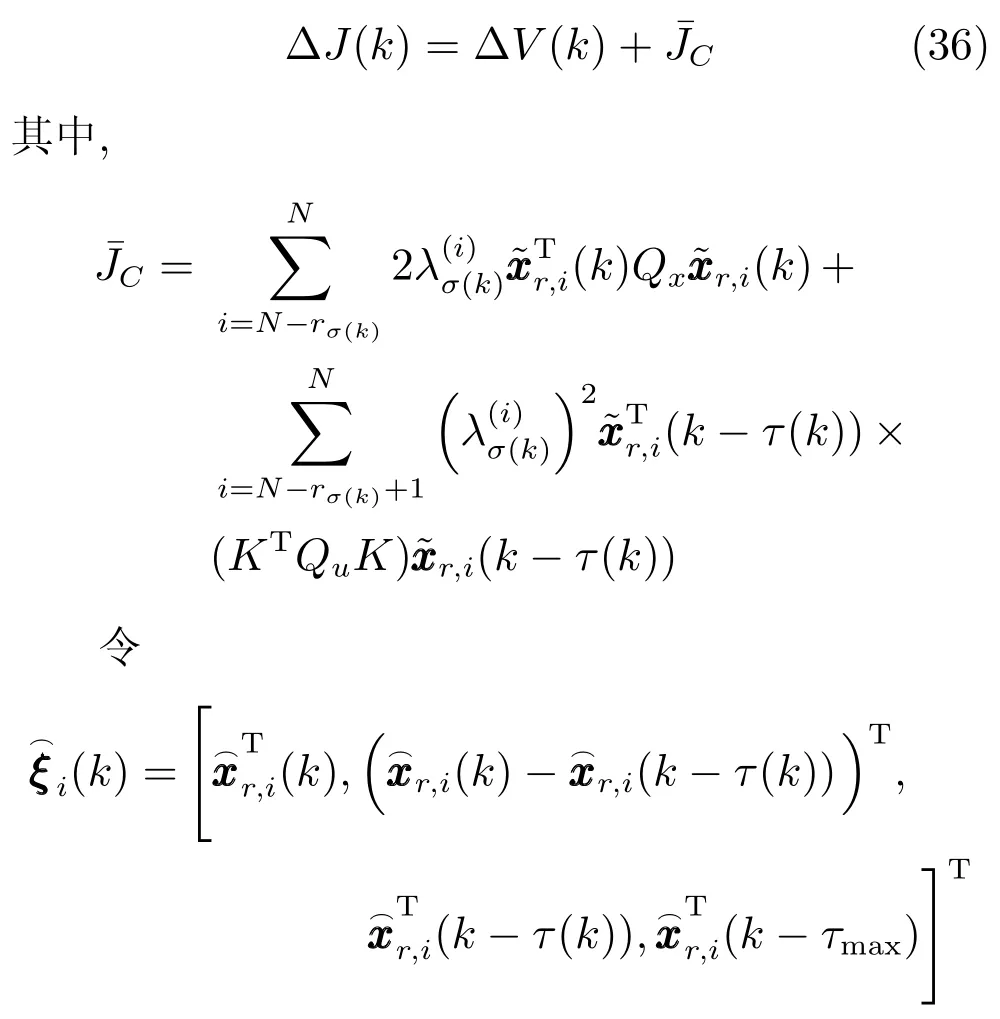
注意到如果∆J(k)≤0,有∆V(k)≤0,接着可以得到

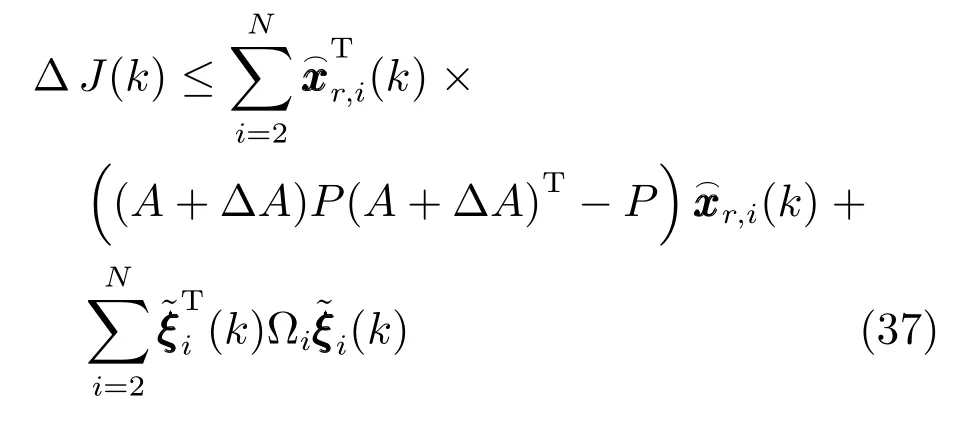
再由线性系统理论知识和凸集优化理论可以得到,如果矩阵不等式(14)和(15)成立,则闭环系统(6)渐近稳定.

从条件(37)和 ∆J(k)≤0可以得到再利用 limk→∞∆V(k)= 0 和,对C≤ −∆V(k)两边进行从k=0到k=∞求和,利用线性系统稳定性理论可以得到JC≤V(0).根据定义可知,矩阵不等式(14)和(15)可确保高阶离散时间不确定多智能体系统(1)获得保性能一致性,并且系统的保性能函数(5)满足JC≤V(0).另外,通过式(7)可以得到.又因为,所以有

由于UUT=IN,所以有和.这样可以得到.又因为x(k)=x(0),k∈{−τmax,−τmax+1,···,0},可以得到V4(0)=V5(0)=V6(0)=0.从而有

根据定义1,综上可得,式(16)是这种情况下保性能函数(5)的一个上界.

注4.引理3利用状态空间分解法,将不确定多智能体系统(1)的鲁棒保性能一致性问题转换为N−1个子系统(9)的鲁棒保性能控制问题,并通过构造合适的Lyapunov函数,寻找到了一个高阶离散时间不确定多智能体系统(1)在时延和切换通信拓扑条件下获得鲁棒保性能一致性的充分条件,并给出了保性能函数(5)的一个与不确定多智能体系统(1)的初始状态x(0)和最大通信时延τmax相关的上界.可行矩阵P,R1,R2,Q1,Q2和K的求解与系统(1)的通信拓扑有关,对保性能函数(5)的上界具有间接的影响.但易发现矩阵不等式(14)和(15)含有非线性不确定项,因此很难利用引理3直接求解出反馈增益矩阵K.

引理4[21].给定合适维的矩阵Y,D和E,且Y是对称矩阵,则

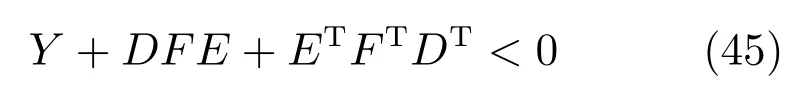
对于所有满足FTF≤I的矩阵F成立的充要条件是存在ε>0满足

引理5[22].线性矩阵不等式

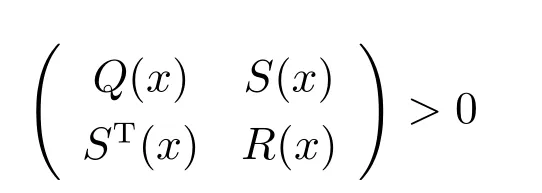
其中,Q(x)=QT(x),R(x)=RT(x)和S(x)与x相关,它等价于

1)Q(x)>0,R(x)−ST(x)Q−1(x)S(x)>0;

2)R(x)>0,Q(x)−S(x)R−1(x)ST(x)>0.

定理1.考虑高阶离散时间不确定多智能体系统(1)的通信时延为τ(k),同时假定它的通信作用拓扑是联合连通的.一致性协议(4)能够解决不确定多智能体系统(1)的鲁棒保性能一致性问题的一个充分条件是存在正数ε1>0,ε2>0,ε3>0,合适维的反馈矩阵K,d×d维的正定矩阵P,S,R1,R2,M1,M2,Q1和Q2是如下优化问题的一个解

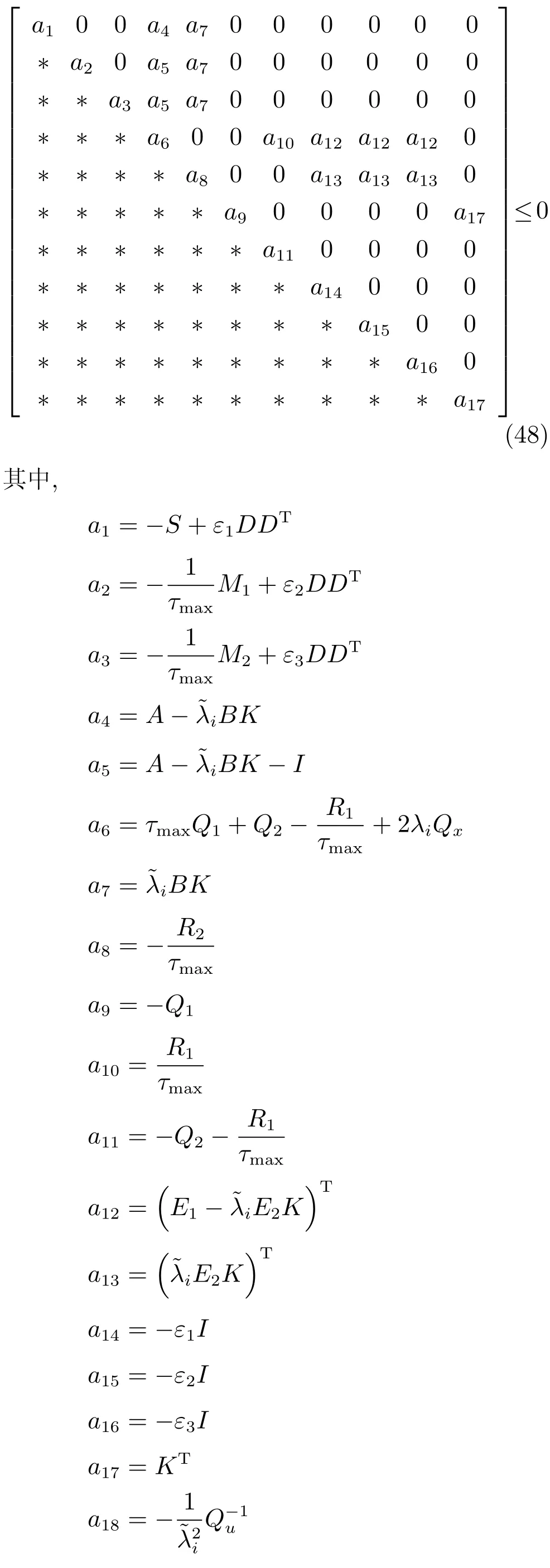
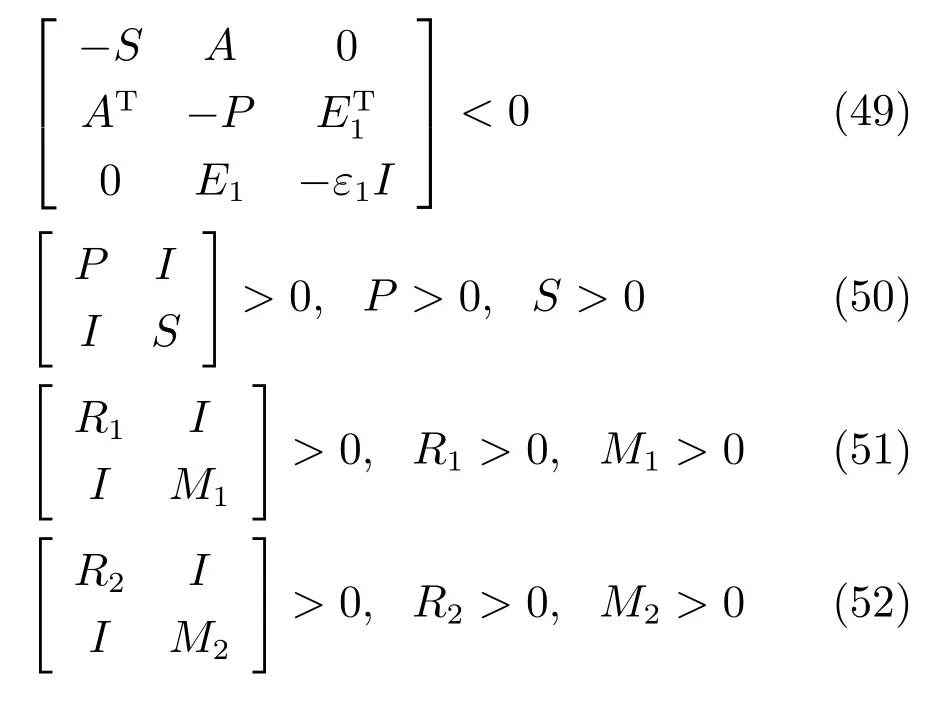
证明.矩阵不等式(14)可写为

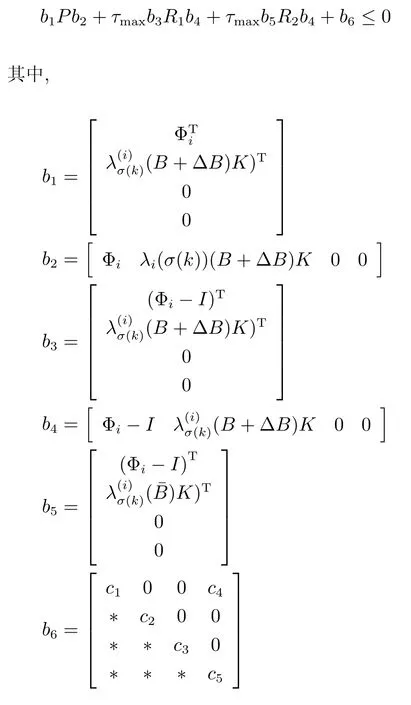
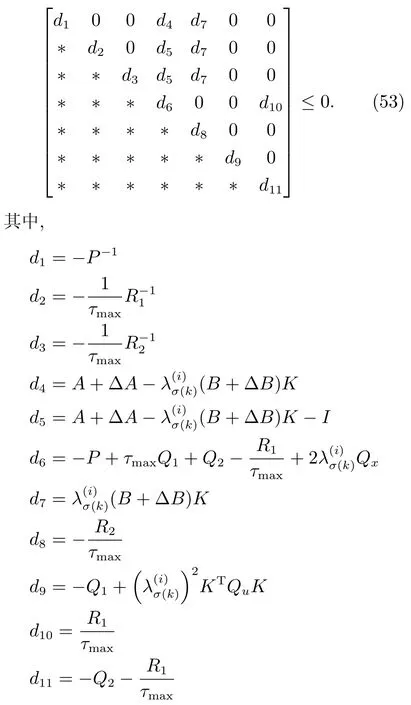
将∆A=DFE1和∆B=DFE2代入矩阵不等式(53),并利用引理4,矩阵不等式(53)对于矩阵F所有可能成立,等价于存在正数ε1>0,ε2>0和ε3>0,满足

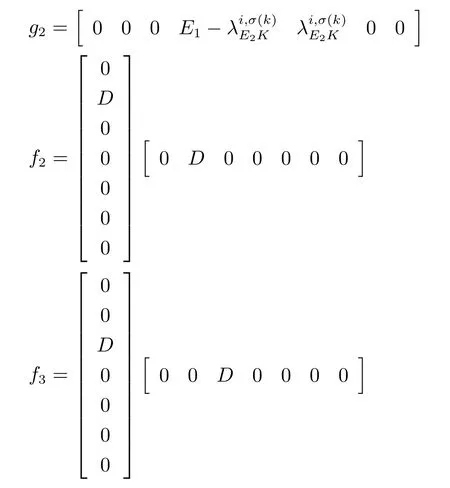
另外,再对矩阵不等式(15)做同样处理.令S=P−1,再利用锥补线性化方法[23]和凸集优化理论,非线性矩阵不等式(54)的求解问题等价于非线性最小化问题(46)∼(51).

注5.通过定理1,非线性线性矩阵不等式(14)和(15)转化为优化问题(46)∼(51),它可以利用算法1进行求解,从而得到反馈增益矩阵,从而使得多智能体系统(1)在一致性协议(4)下获得鲁棒保性能一致性.值得说明的是,因为F是一个未知矩阵,无法直接利用与之相关的不等式条件获得一致性协议的反馈增益矩阵.这种情况下,引理4很好地解决了这个问题.但需注意的是,解K,P,S,R1,R2,M1,M2,Q1,Q2与不确定矩阵D和F密切相关.因为优化问题(46)∼(51)的线性矩阵不等式是堆成的,所以可以利用MATLAB工具箱求解,从而验证其有效性.

算法1.优化问题(46)∼(51)的求解

步骤 1.寻找LMI(46)∼(51)的一个可行解P0,S0,R1,0,R2,0,M1,0,M2,0,如果不存在,就退出.令k=0.

步骤2.令Pk=P0,Sk=S0,R1,k=R1,0,R2,k=R2,0,M1,k=M1,0,M2,k=M2,0,并寻找Pk+1,Sk+1,R1,k+1,R2,k+1,M1,k+1,M2,k+1满足LMI(46)∼(51),并使得tr(PkS+PSk+R1,kM1+R2,kM2+R1M1,k+R2M2,k)最小.

步骤3.如果tr(PkS+PSk+R1,kM1+R2,kM2+R1M1,k+R2M2,k)<6d+ε,则退出.否则,令k=k+1,返回步骤2.

定理2.当闭环高阶离散时间不确定多智能体系统(6)获得保性能一致性时,其一致性序列满足

证明.令.根据式(7),xxx(k)能够被唯一分解为x(k)=xc(k)+xr(k).如前所述,如果闭环不确定多智能体系统(6)获得保性能一致性,则子系统(9)必须Schur稳定,它暗示着子系统(9)由状态xr(0)引起的响应需满足limk→∞ xr(k)=0.因此,一致性序列c(k)完全由xc(k)决定.下面分两种情况讨论一致性序列c(k).

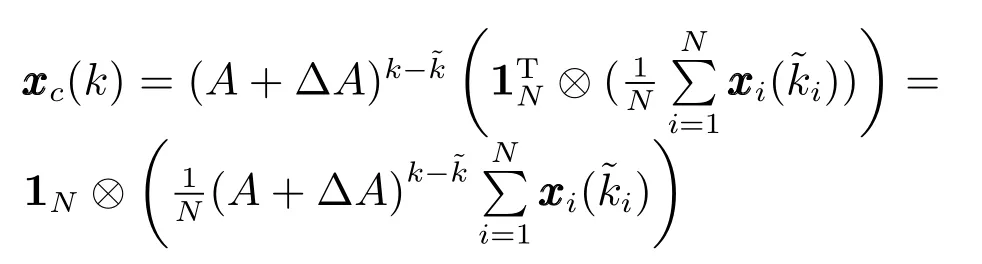
又因为c(k)满足limk→∞(c(k)− xc(k))=0,k=0,1,2,···,综上可得式 (55).

注6.从定理2可以看出,一致性序列c(k)仅与系统矩阵A+∆A、通信拓扑和初始状态x(0)相关,与时间延迟无关.这个条件与文献[12]中的不含不确定性的高阶离散时间多智能体系统情况类似,区别在于定理2描述了不确定性对高阶离散时间不确定多智能体系统的一致性序列的影响.另外值得说明的是,文献[24]利用内模原理解决了异构连续线性多智能体系统的鲁棒一致性控制问题.本文与它的区别在于,文献[24]主要从输出一致性的角度考虑多智能体系统的一致性问题,而本文主要从保性能的角度考虑多智能体的一致性问题.同时,二者考虑的不确定性也有所不同,但还是可以考虑在后续工作将两者结合起来研究.此外,本文工作与H∞控制的区别在于,H∞控制目的在于抑制外部噪声,本文考虑的是节省能量.

4 仿真算例

假定多智能体系统(1)的具体形式如下：

其中,r1,r2和r3是不确定参数,它们满足−1≤r1≤1,−1≤r2≤1和−1≤r3≤1.则高阶离散时间不确定多智能体系统(1)可以重新写为

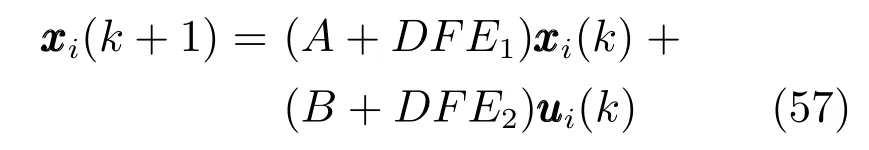
定义保性能代价加权矩阵如下:

设高阶离散时间多智能体系统(1)包含8个智能体,其通信拓扑Gσ(k)是联合连通的,具体如图1所示,图1(a)∼(c)为其3种通信可能,图1(d)为通信拓扑图1(a)∼(c)的合并图.

假定多智能体系统(1)的初始状态为x1(0)=[1,5,−2]T,x2(0)=[2,4,3]T,x3(0)=[1,1,2]T,x4(0)=[3,2,1]T,x5(0)=[5,6,−2]T,x6(0)=[−3,3,4]T,x7(0)=[−2,−4,−3]T,x8(0)=[−5,−2,−1]T.同时,令r1=0.15,r2=0.25,r3=0.15,τmax=3.利用定理1可得K=[0.0422,−0.0549,0.1121]T能够使多智能体系统(1)获得保性能一致性.仿真结果如图2∼6所示.图2∼4给出了多在一致协仪(4)作用下,智能体系统(1)在参数rj(j=1,2,3)变化前后的状态轨迹变化曲线.图2∼4中,◦表示定理2计算出来的多智能体系统(1)的通信拓扑不发生变化的初始一致性序列,∗表示定理2计算出来的多智能体系统(1)的通信拓扑发生变化时的实际一致性序列,其他实线表示多智能体系统(1)状态的变化轨迹.图5给出了保性能指标JC和的变化轨迹.图6给出了多智能体系统(1)的通信拓扑切换信号σ(k)的时序图.

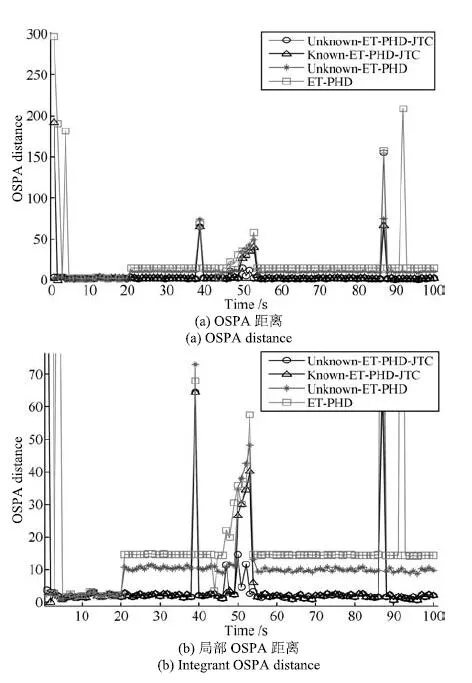
图1 多智能体系统(1)的通信拓扑GFig.1the interaction topology Gof multi-agent system(1)

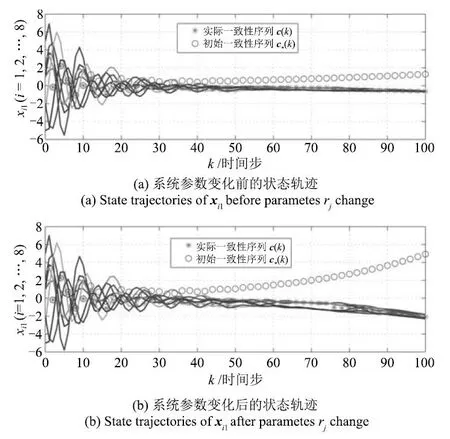
图2 状态xi1在参数rj(j=1,2,3)变化前后的状态轨迹Fig.2Comparison of state trajectories of xi1before and after parameters rj(j=1,2,3)change

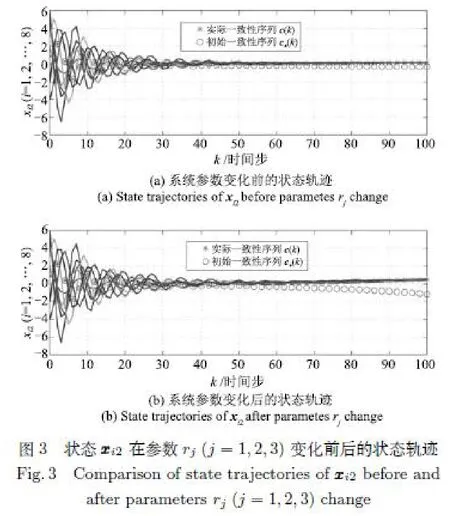
图4 状态 xi3在参数rj(j=1,2,3)变化前后的状态轨迹Fig.4 Comparison of state trajectories of xi3 before and after parameters rj(j=1,2,3)change

从图2∼6的仿真结果可以看出,不确定多智能体系统(1)在一致性协议(4)下获得鲁棒保性能一致性.多智能体系统(1)包含/不包含参数不确定性时,系统都收敛于式(55),与定理2计算出的一致性序列c(k)相同.区别在于当多智能体系统(1)不包含不确定性时,式(55)中的A+∆A需被A取代.多智能体系统(1)的一致性收敛序列与不确定参数rj(j=1,2,3)和系统通信拓扑有关,尤其是图4,可以看出系统一致性序列c(k)会在系统通信拓扑切换时发生突变.图5表明,JC<在实验过程中恒成立,满足定义1的鲁棒保性能一致性要求.实验充分说明了高阶离散时间不确定多智能体系统(1)在定理1求得的增益矩阵K下,受一致性协议(4)作用,能够获得鲁棒保性能一致,从而验证了定理1和定理2的正确性和有效性.

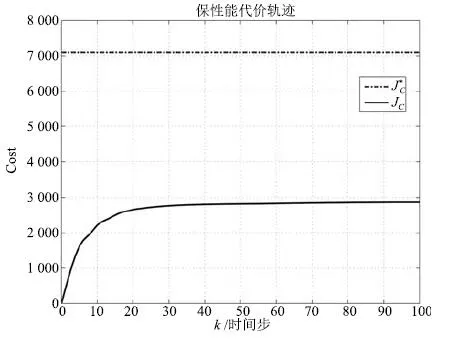
图5 保性能代价轨迹图Fig.5 Trajectories of cost

图6 多智能体系统(1)的通信拓扑切换信号σ(k)Fig.6 The switching signal σ(k)of multi-agent system(1)

5 结束语

在时延和切换通信拓扑条件下,本文对高阶离散时间不确定多智能体系统的鲁棒保性能问题进行了研究,给出了高阶离散时间不确定多智能体系统获得鲁棒保性能一致性的一个充分条件,并提供了其保性能函数的上界和一致性序列.数值仿真验证了本文所提理论的正确性.另外,本文所提方法较为复杂,后续工作将考虑如何使其简化.