基于ET-PHD的自适应联合跟踪与分类算法
樊鹏飞 李鸿艳
目标的跟踪与分类问题已经成为监视系统中两个重要的组成部分,联合跟踪与分类(Joint tracking and classification,JTC)技术将这两个问题放在统一的框架下进行研究[1].采用JTC技术带来的裨益是充分利用跟踪器和分类器的耦合性,同时有效地提高目标的跟踪精度和识别能力.随着观测传感器分辨率的提高,现代传感器可以获得一个目标的多个观测点,这些观测点不仅包含了目标的运动学信息,同时还提供了目标的形态信息,目标在这种情况下被称作扩展目标(Extended target,ET)[2].近年来,扩展目标跟踪已有了大量研究成果,然而对于扩展目标的联合跟踪与分类问题却鲜有研究.Lan等[3]将形态信息作为属性信息,在随机矩阵框架下实现了对椭型扩展目标的联合跟踪与分类.之后他们利用多个椭型近似拟合非椭型扩展目标,建立可以描述类别相关的包含先验信息的系统模型,实现了对非椭型扩展目标的联合跟踪与分类[4].文献[5]在贝叶斯风险框架下,通过最小化目标状态估计与类别决策的贝叶斯风险来解决扩展目标的联合跟踪与分类问题.文献[6]建立了基于支持函数和扩展高斯映射的状态模型,用以分别描述平滑扩展目标和非平滑扩展目标,将类别信息加入到支持函数中,改善扩展目标的跟踪与分类性能.上述的联合跟踪与分类算法是在单目标贝叶斯滤波基础上,针对无杂波、无漏检和单目标的情况.Mahler[7]利用随机有限集对目标状态集和观测集进行建模,实现了最优多目标贝叶斯滤波器.概率密度假设(Probability hypothesis density,PHD)是定义在状态空间上随机有限集的一阶矩,使用PHD滤波器近似最优多目标贝叶斯滤波器可以使复杂度得到有效降低.PHD滤波器实现了无数据关联的多目标跟踪,结合JTC技术能够有效改善目标数目以及状态估计的精度,同时更为精确的估计结果又保证了目标分类性能[8−9].然而,标准PHD滤波器将目标视为点目标,无法处理扩展目标跟踪问题.2009年,Mahler采用文献[10]中的泊松分布量测模型,推导出ET-PHD滤波[11],首次将随机有限集理论引入到扩展目标跟踪中,为扩展目标跟踪提供了一个新的数学理论框架.然而,ET-PHD滤波器包含多重积分运算,无法得到解析解.文献[12]给出了ET-PHD滤波器的高斯混合实现方式,即ET-GM-PHD滤波器,文献[13]证明了该算法的收敛性.为了使该滤波器应用范围更广,众多学者进行了许多研究工作.文献[14]针对杂波密度大、近邻扩展目标的情况提出了归一化的ET-GM-CPHD滤波算法.针对多机动扩展目标的跟踪问题,文献[15]采用跳变马尔科夫系统模型对ET-GM-CPHD滤波器进行扩展,取得了良好的机动跟踪效果.
新生目标强度是PHD滤波器的重要组成部分,传统的滤波器假定新生强度先验已知,实际上新生目标可能在监视区域中任何位置出现.另外,新生目标的类别信息也是未知的,这些先验信息对多目标的跟踪算法性能产生很大影响.有学者提出一类量测驱动的PHD滤波器,利用每一时刻的量测起始新生目标[16−17].然而,这类算法在起始新生目标时仅仅利用了量测的位置信息,无法起始不同类别的新生目标强度,不能直接应用在JTC技术中.文献[18]提出两级自动联合跟踪与分类算法,能够克服新生目标的类别信息先验已知的假设,但是这种算法将分类与跟踪分别放在两个阶段,状态与分类之间的信息交互并不充分.
针对扩展目标的联合跟踪与分类问题及先验未知的新生目标强度,本文提出一种基于ET-PHD的新生目标强度未知情况下的扩展目标联合跟踪与分类算法,并给出改进算法的高斯混合实现方法,来改善ET-PHD滤波器在扩展目标跟踪中的性能.各个类别的新生目标强度由传感器获得的量测生成,将存活目标与新生目标分别进行预测,之后利用联合量测似然对预测后的后验目标强度进行联合更新,获得各个类别的目标状态集.
1 基于ET-PHD的联合跟踪与分类算法
假设场景中可能共有C类扩展目标,目标的类别标签集为Θ={1,2,···,C}.k时刻存在N(k)个扩展目标和M(k)个位置量测以及M(k)个属性量测,其中Xk和分别为扩展目标的状态集和量测集.
类似于ET-PHD滤波器,基于ET-PHD滤波的联合跟踪与分类算法(ET-PHD-JTC)主要包括预测和更新两个部分.ET-PHD-JTC算法是在已知类别集合下,对状态、数目、所属类别未知情况下扩展目标的跟踪与分类,关键在于重构目标状态的类别条件PHD.对于第c(c∈Θ)类目标,Dc,k(xk)和Dc,k|k−1(xk)分别表示第c类多目标条件后验概率密度和的一阶近似矩,将条件PHD代入到ET-PHD滤波中,则ET-PHD-JTC滤波器的预测步骤为[12]
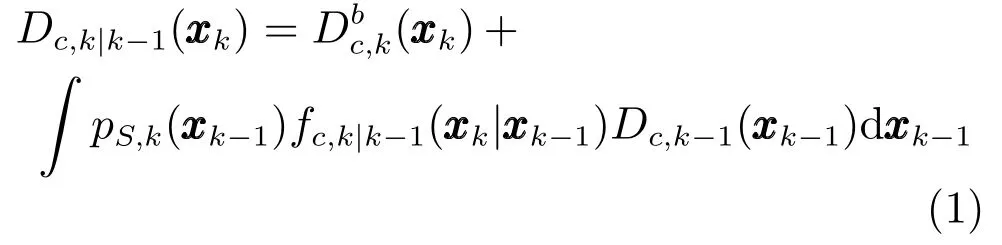
在k时刻c类扩展目标的PHD更新为[12]
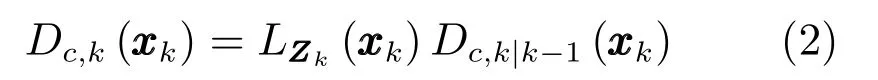
式(2)中的量测伪似然函数定义为
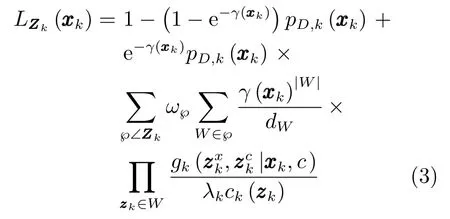
其中,γ(·)为扩展目标产生量测的期望个数,pD,k(·)为目标的检测概率,λk为观测区域中杂波量测的期望个数,ck(zk)为杂波的空间分布概率密度,为单目标的联合似然函数,代替了原ET-PHD滤波算法中的单目标位置似然函数.℘∠Zk为量测集Zk的℘种量测集划分,W∈℘为属于第℘种划分的非空量测子集,|W|表示子集中包含的量测数目,ω℘和dW分别为每种划分和划分子集的权重,定义为
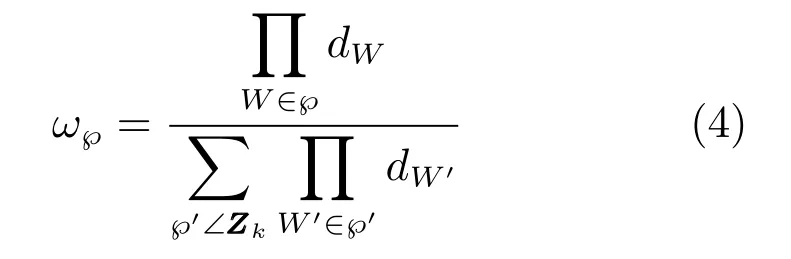
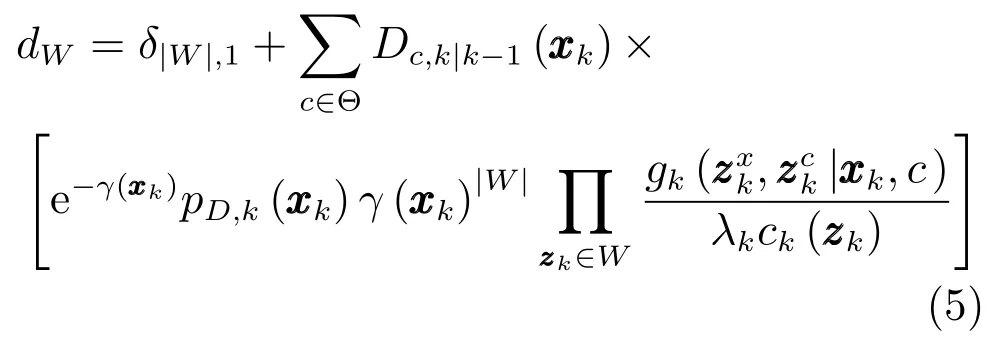
其中,δ|W|;1为克罗内克函数.注意式(5)与文献[12]中ET-PHD滤波器的不同.
量测集的划分是ET-PHD滤波的重要部分,本文的核心是研究扩展目标的联合跟踪与分类算法,量测集的划分并不是研究重点.本文采用文献[12]中的距离划分.
k时刻更新后完整的扩展目标PHD为
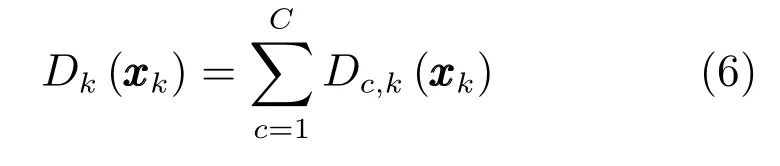
2 自适应ET-PHD-JTC滤波器
在k时刻,将扩展目标划分为存活目标和新生目标,并对两类目标分别进行ET-PHD的预测和更新.使用标签β区分存活目标与新生目标,即

在不失合理性的前提下,作如下假设:
1)目标的存活概率与检测概率是时不变且与状态无关,即pS,k(·)=pS和pD,k(·)=pD.
2)杂波概率密度服从均匀分布且杂波个数服从泊松分布.
3)扩展目标产生量测个数服从泊松分布,泊松率与状态无关,即γ(·)=γ.
5)目标的运动模型和位置量测模型是非线性高斯演化模型,即
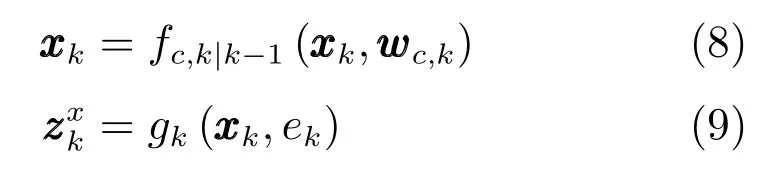
其中,fc,k|k−1(·)为第c类目标的动态模型函数,wc,k是均值为µc,k方差为Qc,k的高斯过程噪声;gk(·)为量测模型函数,ek为均值是εk方差为Rk的高斯量测噪声.
在式(1)的基础上,新生目标强度未知的自适应ET-PHD-JTC滤波器的预测步骤为
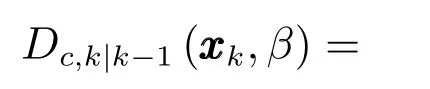
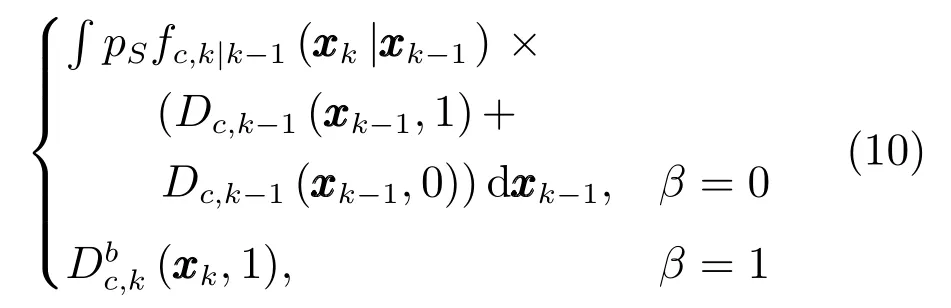
存活目标(β=0)的更新方程为
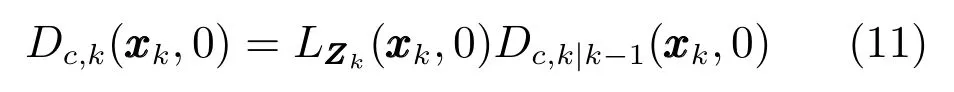
式(11)中的伪似然函数为
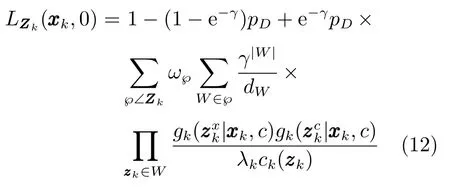
新生目标(β=1)的更新方程为
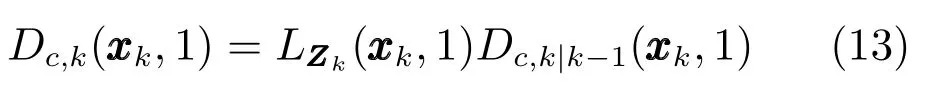
新生目标从量测集获得,因此新生目标总是能被检测到,即pD=1,式(13)中的伪似然函数为
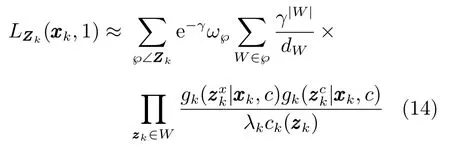
在式(5)的基础上,式(12)和式(14)中的权重dW变为如下表达式:

3 高斯混合实现方法
3.1 预测
假设k−1时刻得到的c(c∈Θ)类后验目标强度是高斯混合形式的,即

k时刻用于预测β=0情况的高斯项为上一时刻存活目标和新生目标两部分高斯项的并集,即
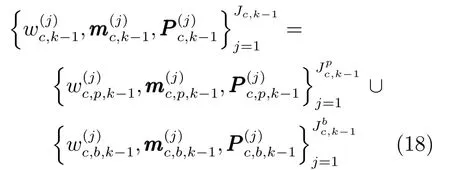
由于运动模型和量测模型中fc,k|k−1(·)和gk(·)均为非线性函数,上一时刻由高斯混合项近似的后验PHD若直接利用第2节中的PHD递推公式求解,得到的后验PHD并不是高斯项和的形式.为了得到高斯混合项的结果,需要寻找一种能够计算经过非线性变换的随机变量统计特性的方法.无迹变换(Unscented transformation,UT)可以根据随机变量的统计特性产生确定的Sigma采样点,这些采样点通过非线性函数传播后可以直接求出估计值的均值和协方差.UT变换的算法流程如算法1所示.
算法1.UT变换
输入.n维随机变量x,其均值为m、方差为P.
输出.Sigma采样点集.
步骤1.Sigma采样点选取规则.
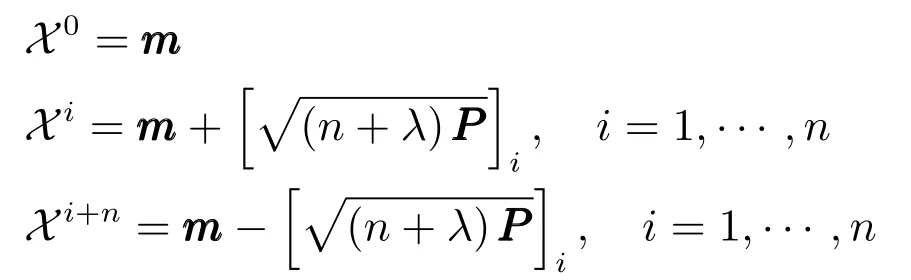
其中,参数λ=α2(n+κ)−n决定了采样点与均值之间的距离,参数α通常取一个较小的正数(10−4≤α<1),κ通常取0或3−n,[·]i为矩阵的第i列.
步骤2.Sigma采样点权值计算.
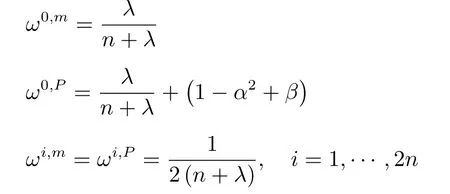
其中,带有上标m为估计均值时的权值,带有上标P为估计协方差时的权值.根据随机变量x的统计分布,β取不同的值,对于高斯分布,β=2为最优值.
由于过程噪声与量测噪声均为非加性高斯噪声,因此首先要将状态变量扩维包含噪声变量,然后进行UT变换.将式(18)中的每一项高斯分量进行扩维,状态变量扩维成其中扩维状态变量的维数为n′,状态变量的维数为n,过程噪声状态变量µc,k|k−1的维数为nw,量测噪声状态变量εk的维数为ne.扩维向量经过UT变换可以获得其Sigma采样点集为第j个扩维状态变量的第i个采样点.这些采样点经过式(8)的动态非线性模型函数传播后,得到存活目标(β=0)的预测后验PHD.存活目标的预测强度也是高斯混合形式的,可表示为

各个类别的新生目标强度由传感器获得的量测驱动生成,即新生目标PHD由量测划分子集W反演得到.由于并没有使用到运动模型,因此这里随机变量的扩维不包含过程噪声.量测扩维成,其中为划分量测子集W中的量测均值,根据式(9)中的量测模型,划分子集W中的量测协方差为Rk,扩维量测变量的维数为m′,量测变量的维数为m.扩维向量经过UT变换可以得到其Sigma采样点集为第W个划分子集中扩维量测变量的第i个采样点.这些采样点经过量测非线性模型反函数的传播后,获得新生目标(β=1)的预测PHD.新生目标(β=1)的预测强度表示为

其中,|℘|为第℘种划分中子集W的量测个数,vc,b,k|k−1为第c类新生目标期望个数,为量测模型函数的逆函数,以及
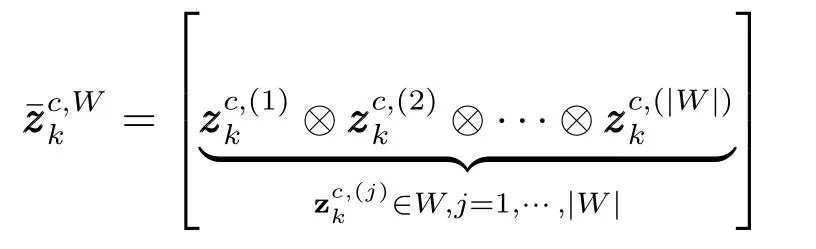
为划分子集中属性量测的融合均值,⊗为融合算子,根据属性信息的不同需要采用不同的融合规则[19].
3.2 更新
更新步骤根据量测模型对Sigma采样点进行非线性变换,这里不再对预测后的高斯混合项重新进行UT变换,而直接利用预测后得到的Sigma采样点, 牺牲部分精度以减小算法复杂度.在式(11)和式(12)的基础上,存活目标强度函数更新为
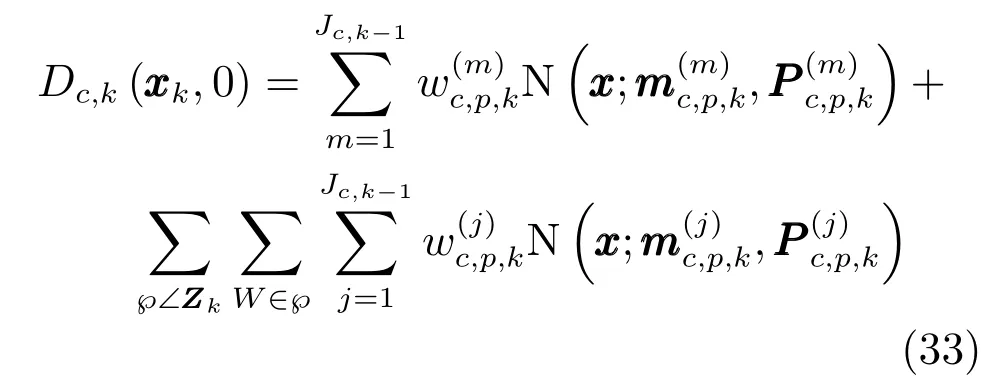
其中,未检测部分的高斯项为
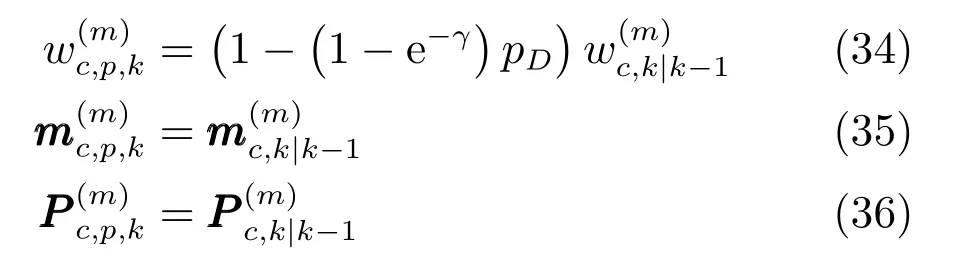
检测部分的高斯项为

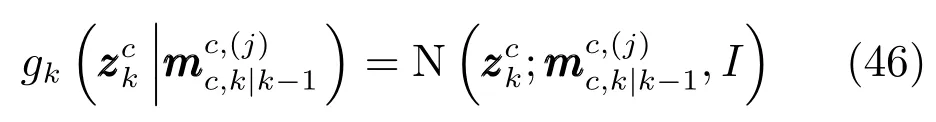
其中,I为单位矩阵
在式(13)和式(14)的基础上,新生目标强度函数更新为
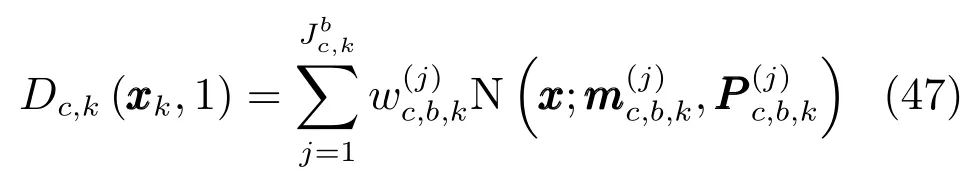
与存活目标不同,新生目标强度函数高斯项的更新仅含有检测部分.式(47)中新生目标强度函数高斯项计算公式为
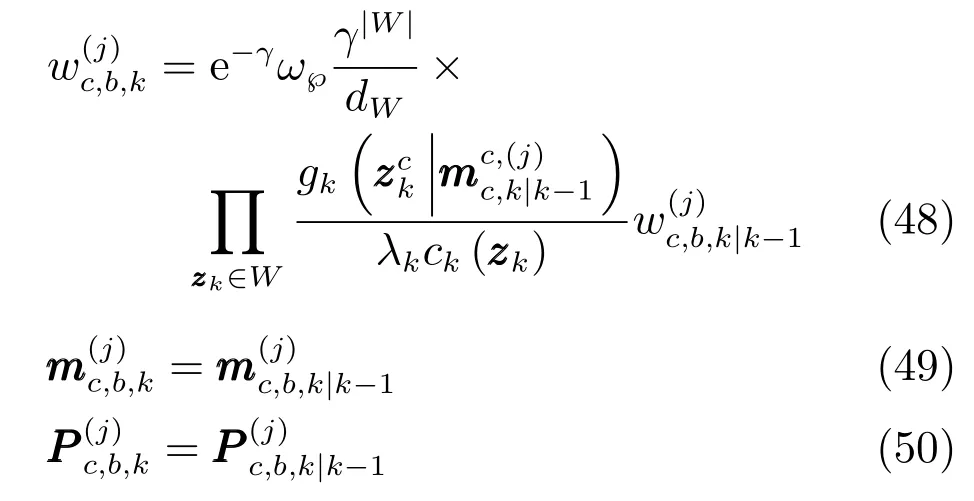
式(42)和式(48)中权重dW计算为
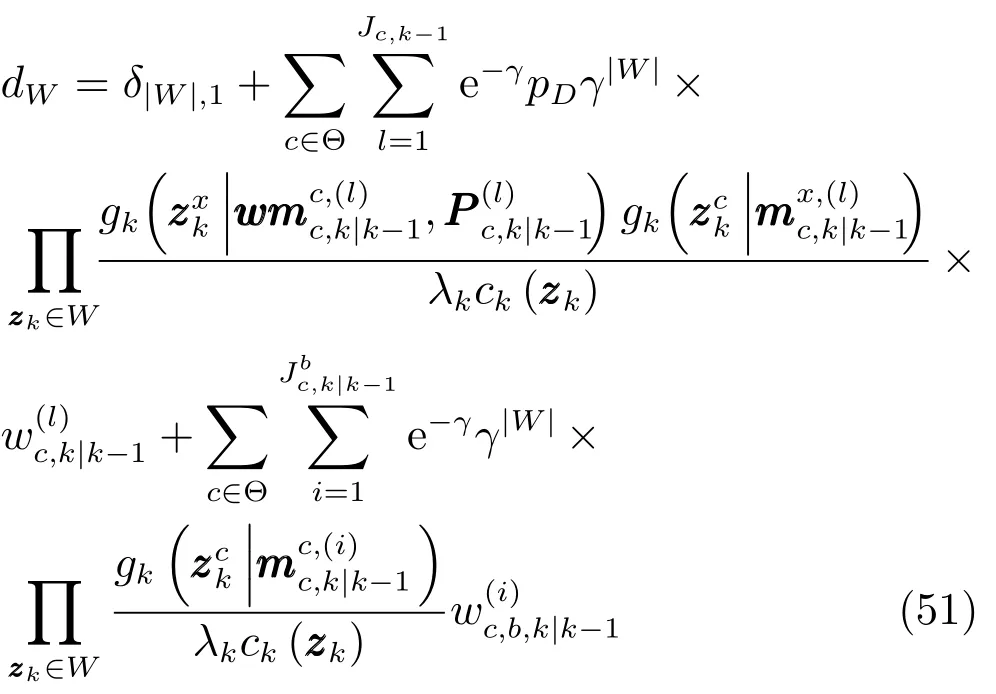
3.3 删减与合并
高斯混合实现算法的高斯项会随着时间不断增加,k时刻更新后高斯混合项的个数为
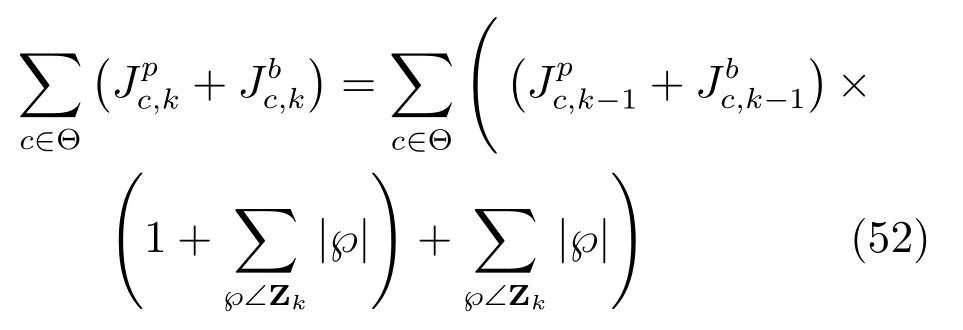
从式(52)可以看出,后验目标强度中的高斯项的个数将无限增长,因此,如果不对高斯项进行删减,整个算法是不可行的.若每一类目标后验强度分别进行高斯项的删减合并,则会大大增加算法的计算量.为减少计算量,将更新后的所有高斯项进行删减合并.本文基于文献[12]给出的启发式删减合并算法来有效地减少异类高斯混合项的个数,该算法的主要思想是:1)保留权重较大的高斯项;2)合并距离相近的同类高斯项.
合并判决表达式变为
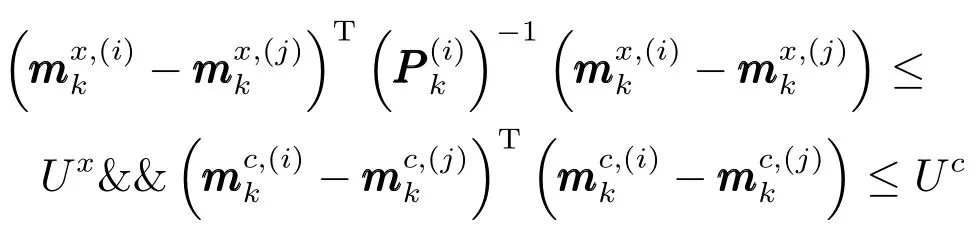
其中,Ux为运动学信息判决门限,Uc为属性信息判决门限,决策融合采用“与”规则.其他参数计算与文献[12]一致.
最后,提取多目标状态集:
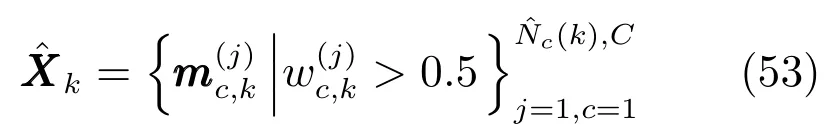
为了更清楚地说明改进算法,对k时刻完整的该算法各个步骤总结如下:
算法2.k 时刻自适应滤波器算法流程
输入.
k−1时刻存活目标高斯项和新生目标高斯项,k时刻量测集
输出.
k时刻的存活目标高斯项和新生目标高斯项,估计状态集k.
步骤1.量测集划分
步骤2.预测
对式(18)中的高斯分量进行扩维
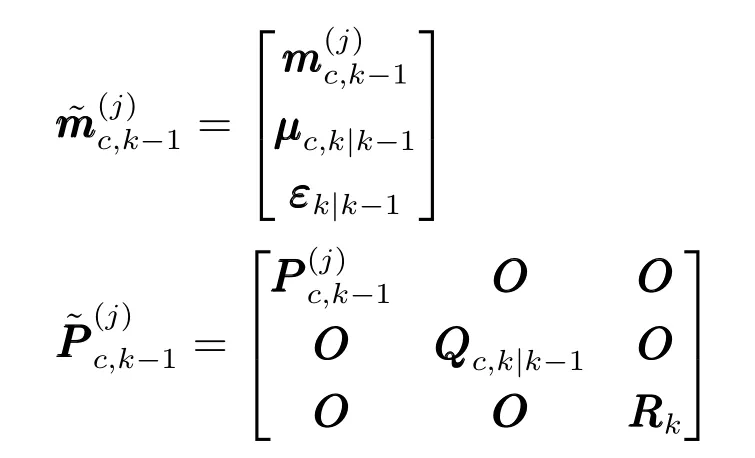
对量测划分子集W中的量测均值高斯分量进行扩维
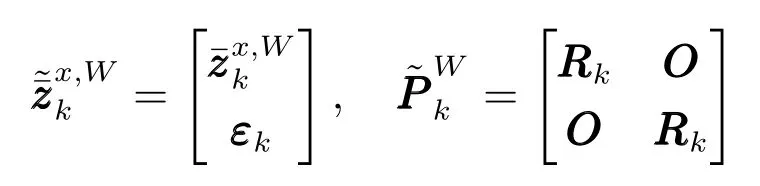
步骤3.更新
通过式 (34)∼(45)更新存活目标的高斯项,未检测部分的属性信息保持不变,检测部分的属性信息通过式(44)进行更新;通过式(48)∼(50)更新新生目标的高斯项.
步骤4.高斯项的删减与合并
参考文献[12],通过式(53)合并高斯项.
步骤5.状态估计
通过式(54)计算扩展目标状态集.
4 仿真实验
4.1 场景及参数设置
为验证本文所提的新生目标强度未知的ETPHD-JTC(Unknown-ET-PHD-JTC)滤波算法,构建一个包含三类目标并行、交叉运动的仿真场景,期间存在目标新生与消亡过程,并与新生目标强度先验已知的ET-PHD-JTC(Known-ET-PHDJTC)滤波算法、新生目标强度先验未知的ETPHD(Unknown-ET-PHD)滤波算法以及文献[12]中原ET-GM-PHD滤波算法的结果进行比较.
监视区域为[−800m,800m]×[−800m,800m],k时刻目标质心状态向量为
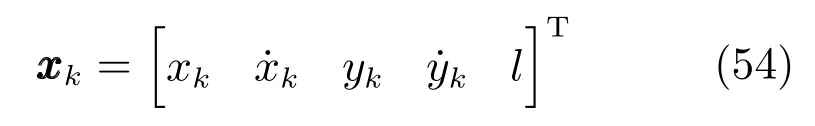
其中,xk和yk为目标的二维位置,k和k为相对应的速度,l为扩展目标的长度.
为简化仿真,假定异类目标的运动模型和量测模型相同,采样时刻为T=1s,目标的运动方程为
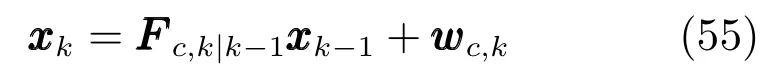
其中,模型参数为
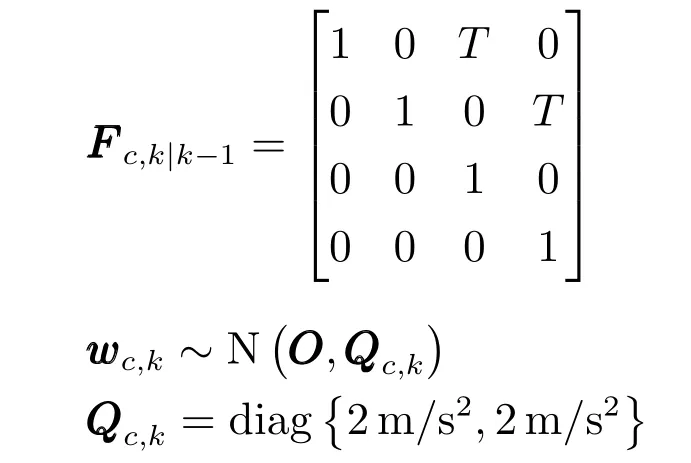
量测方程为
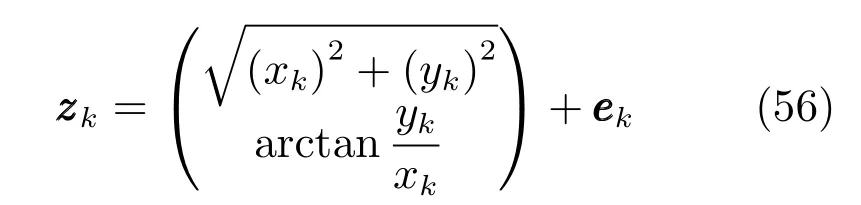
其中,模型参数为
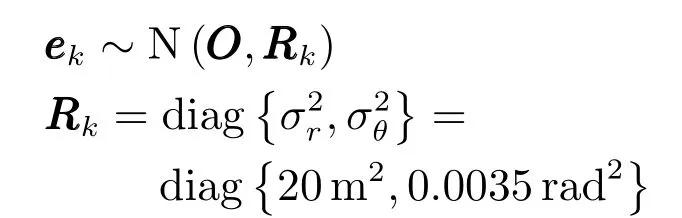
仿真中属性量测为HRR雷达可以获得的纵向距离像Lk(xk),其量测方程为[20]
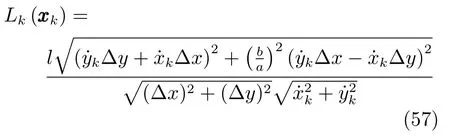
其中,∆x=xk−xr,∆y=yk−yr,(xr,yr)为传感器坐标,设为原点坐标,b/a表示扩展目标的纵横比.
仿真中目标的存活概率设置为pS=0.99,检测概率为pD=0.99,目标产生量测的期望个数为γ=10.杂波过程为均匀分布的随机有限集,杂波期望个数为λk=10.对于每一个量测zk,式(29)中的逆函数为
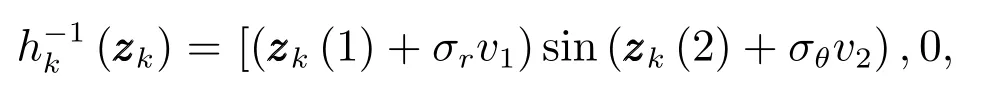
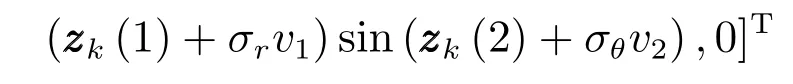
其中,zk(1)和zk(2)分别为量测向量的第1项和第2项,v1,v2∼N(0,1).
另外,新生目标强度先验已知的扩展PHD-JTC滤波算法的新生PHD为
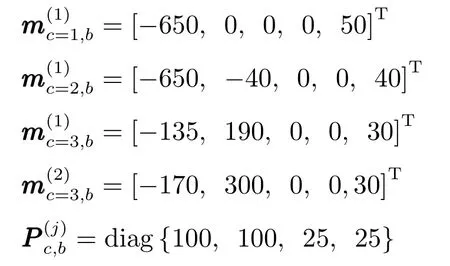
4.2 仿真结果与分析
图1是三种类别四个扩展目标的轨迹与所提算法的目标位置估计图,其中起始点和终止点分别用圆和三角形标识出来,并行时目标间距为40m.从图1中可以看到,所提算法能够正确估计异类目标的状态.目标3和目标4属于同一类扩展目标,所提算法与ET-GM-PHD算法存在相同的问题,即多个高斯分量描述同一个强度峰值,无法更为精确地估计同类目标的状态.
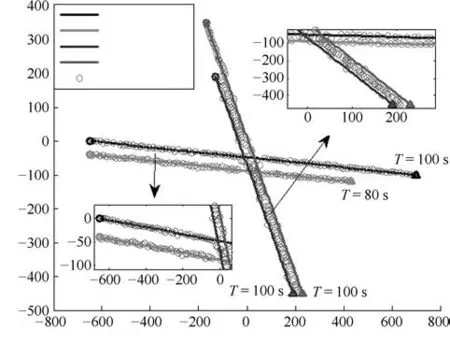
图1 真实轨迹与估计值Fig.1 True traces and measurements
目标数目估计是评价多目标跟踪算法性能的重要指标.为了使对比效果更为明显,用高斯分量权重和代替估计的目标数目.图2是四种算法经过100次蒙特卡洛仿真的平均权重和估计、估计值与真实目标数目之间误差的绝对值以及目标数目估计的标准差结果.Unknown-ET-PHD滤波算法中未知新生目标强度的自适应估计方法与本文所提方法相同.从图2(a)和2(b)来看,当处于1∼80s时,改进算法与Known-ET-PHD-JTC滤波算法相比于Unknown-ET-PHD和ET-GM-PHD滤波算法对目标数目的估计更接近真实目标数目,能够更为精确地估计目标数目,验证了联合跟踪与分类技术在扩展目标跟踪方面的优势,而81s之后,场景中不存在异类扩展目标,联合跟踪与分类技术不再发挥其效能.在新生目标出现以及目标发生交叉时,由于目标处于近邻状态,Known-ET-PHD-JTC滤波算法对目标数目的估计会产生较大偏差,所提算法在式(27)∼(32)起始新生目标强度时充分利用量测信息,有效地克服了Known-ET-PHD-JTC滤波算法的不足.
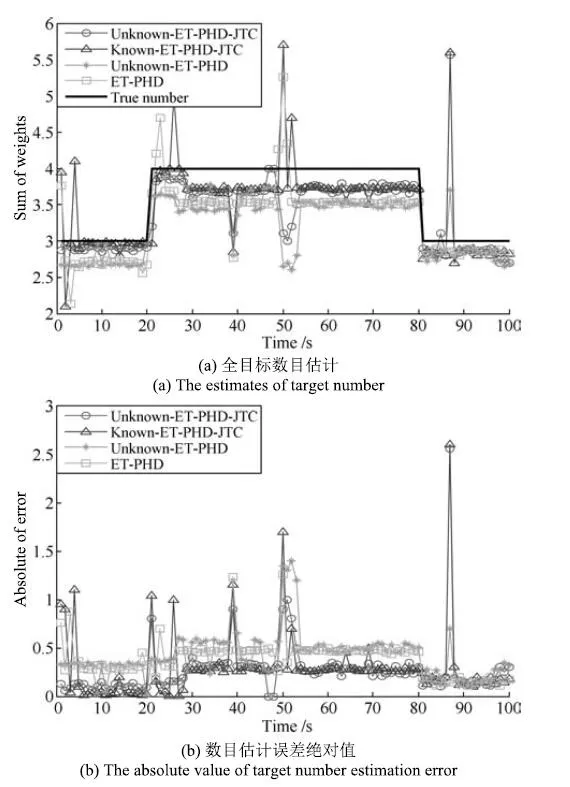
图2 目标数目估计的性能比较Fig.2 The performances of target number estimation
图3是所提UnKnown-ET-PHD-JTC与Known-ET-PHD-JTC两种算法分别对三类目标数目的估计结果对比图.从图3可以看出,所提算法可以较好地估计各类扩展目标的数目,当目标发生交叉时,由于量测集的划分采用基于距离的简单划分方法,滤波仍会产生漏估计[12],数目估计会产生较大偏差,然而,相对于Known-ET-PHD-JTC滤波算法,改进算法充分利用目标的属性信息,因此出现较大偏差估计的时间较短,仍然能够有效估计近邻目标的数目.
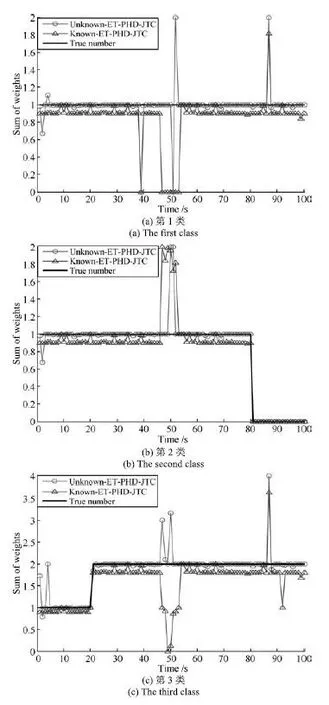
图3 各个类别目标势估计Fig.3 The estimates of target number of each class
由于多目标估计后的目标个数与真实的目标个数有可能不相等,因此采用一般衡量目标跟踪性能的均方根误差不再适用.采用OSPA距离来度量多目标估计算法的跟踪误差,其定义为
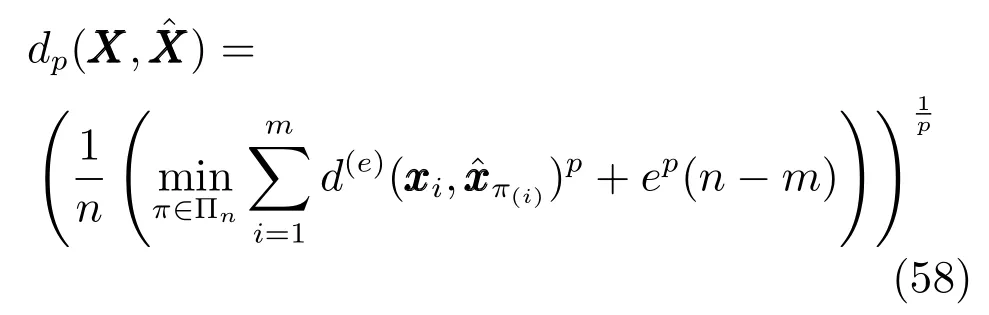
其中,m和n分别为集合X,的势,Πn表示集合{1,2,···,n}上的排列组合,e与p为距离参数.文献[21]指出,较大的e值强调势误差部分而弱化定位误差部分,较小的e值强调定位误差部分而弱化势误差部分,参数p决定了对异常值的敏感性.由于已经对比了目标数目的估计结果,这里OSPA距离的估计强调定位误差弱化势误差部分,将仿真中参数设置为e=30和p=1.
图4是经过100次蒙特卡洛仿真后,四种滤波算法的OSPA距离,图4(a)为完整的OSPA距离,图4(b)为局部放大后的OSPA距离.所提算法与Known-ET-PHD-JTC滤波算法的OSPA距离明显小于Unknown-ET-PHD和ET-GM-PHD滤波算法,验证了联合跟踪与分类技术在扩展目标跟踪精度性能方面的优势.另外,在新生目标出现时,所提算法的OSPA距离小于Known-ET-PHDJTC滤波算法,并且在整个仿真时间内所提算法的OSPA距离始终维持在一个较低的水平.因此,所提算法在新生目标强度未知以及目标处于并行、交叉情况下对多扩展目标状态与类别的估计有明显优势.
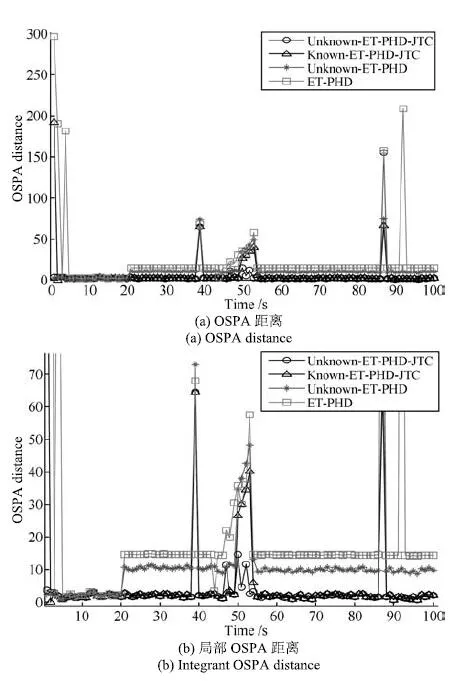
图4 OSPA距离Fig.4 The OSPA distances
在时间开销方面,所提算法与Known-ETPHD-JTC滤波算法相比,算法复杂性上只是多了一个新生目标强度估计的复杂度,每一类目标强度多增加了个高斯项.与Unknown-ET-PHD滤波算法相比,增加的高斯项为.所提算法的每步平均时间开销为1.33s,原ET-GM-PHD滤波算法为0.98s.
表1给出了四种滤波算法性能的具体参数,与图2∼4相对应,改进算法与Known-ET-PHD-JTC滤波算法在性能上比Unknown-ET-PHD和ETGM-PHD滤波算法都有很大提升,验证了联合跟踪与分类技术在扩展目标跟踪的目标数目估计和定位精度方面具有优势,另外所提算法可以在新生目标未知情况下很好地自适应起始新生目标强度.在时间开销上,改进算法增加了原ET-GM-PHD算法时间开销的35.71%.
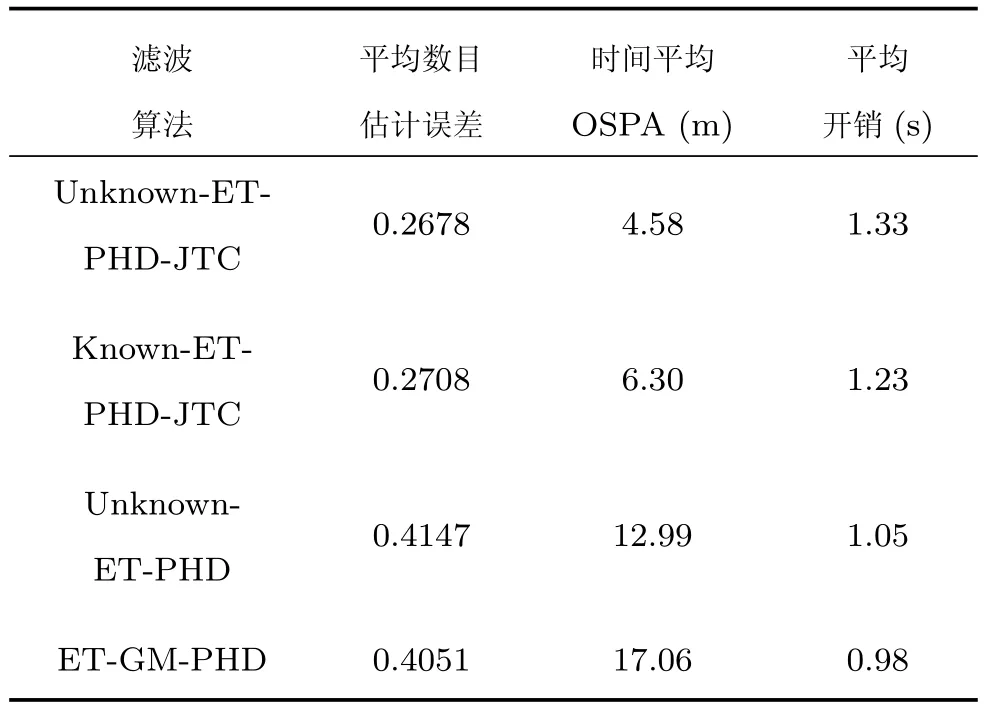
表1 不同方法的滤波性能对比Table 1 The performance versus of different filters
5 结论
针对扩展目标联合跟踪与分类问题及先验未知的新生目标强度,提出一种基于扩展目标概率假设密度滤波器在新生目标强度未知情况下的联合跟踪与分类算法.该算法在扩展目标概率假设密度滤波器的基础上,利用属性信息与目标类别的似然关系,实现不同类别目标强度在滤波器中的估计.算法能够自适应地起始各个类别的新生目标强度,使滤波器能够及时地实现跟踪.仿真结果表明,提出的自适应扩展目标联合跟踪与分类算法改进了概率假设密度滤波器在扩展目标跟踪中的性能.

