基于FERC模型的油品流淌火灾定量风险评估方法研究*

李云涛，陈旭芳，帅 健

(中国石油大学(北京) 安全与海洋工程学院，北京 102249)

0 引言

流淌火在油品的储存、运输过程中时有发生。当油品泄漏发生在边界不受限制的区域时，液池会在重力的作用下扩展。此时如果被点燃，则会一边流淌一边燃烧，形成流淌火。流淌火的燃烧面积不断变化，产生的高温和热辐射等会对周边的设施及人员安全产生威胁，甚至引发更大规模的火灾、爆炸事故。2010年大连7.16输油管道爆炸事故中，自管道内泄漏的原油在很短的时间内即形成了2 500 m2的流淌火[1]。2016年4月22日，江苏靖江德桥仓储有限公司的油品管线泄漏着火，燃烧的汽油向两侧道路迅速流淌，损毁周边管道及储罐，致使火势加剧，最终形成燃烧面积超过2 000 m2的流淌火[2]。流淌火是造成事故态势扩大、引发连锁灾害的1个重要原因。因此，针对油品流淌火开展风险评价，对于油品储运的安全保障具有重要的意义。

目前针对流淌火灾的风险评价尚无较好的模型。在常见的定量风险评估(QRA)方法中，对于边界不受限制区域内的泄漏，并不考虑流淌火的动态变化过程。通常的做法是用泄漏总量除以临界油膜厚度值，以此估计火灾的燃烧面积。其中，泄漏总量一般可根据储罐内的介质量，或是管道泄漏速率和泄漏时间决定；临界油膜值则与地表类型有关[3]。由于在流淌火燃烧过程中，泄漏的油品因燃烧而不断消耗，如果仅考虑泄漏总量的话，在一定程度上会高估流淌火的最大燃烧面积，与实际情况并不相同。因此，有必要结合流淌火蔓延模型分析其燃烧面积变化的动态过程，建立相应的风险评价方法。

流淌火蔓延模型来源于液化天然气(LNG)的液池扩展模型，将其中的蒸发速率替换为燃烧速率，则可用于描述流淌火的蔓延过程。常见的有Fay模型[4]、Lehr模型[5]、FERC模型[6]、SNL模型[7]和基于“重力-粘性”平衡的流淌火蔓延模型[8]等。这些模型多是从不同的油膜扩展模型(运动方程)发展而来，将燃烧速率(蒸发速率)看作是油膜厚度的下降速率(质量方程)，并假设油膜厚度低于某临界值时油池停止扩展，进而求解并预测随时间变化的流淌火燃烧半径。笔者曾对比了Fay模型、FERC模型和计算流体力学软件FLACS的计算结果，证明了FERC模型与FLACS 的数值模拟结果接近且偏于保守[9]。因此，本文将基于FERC模型开展流淌火灾风险评价方法研究。

1 模型介绍

1.1 FERC流淌火模型

FERC模型是ABS咨询公司在美国联邦能源管理委员会(FERC)的资助下研发的流淌火灾模型，该模型考虑了摩擦力和油膜形状对液池扩展的影响，包括运动方程和质量方程2部分[6]。

运动方程为：

(1)

式中：r为液池半径(燃烧区域半径)，m；t为时间，s；g为重力加速度，m/s2；Δ为液面以上部分的油膜厚度所占的比例，Δ=(ρW-ρL)/ρW，ρW和ρL分别为水和液体的密度，kg/m3，对于地面流淌火，Δ=1；Φ为形状因子，与前沿油膜厚度hf和油膜平均厚度h的比值有关；CF为摩擦阻力，m/s2。关于Φ和CF的取值，可参见文献[10]。

质量方程为：

(2)

式中：Ap=πr2为液池面积，m2；Vp=Aph为液池中的油品体积，m3；Qin,m为油品的质量泄漏速率，kg/s；mv为燃烧速率，kg/(m2·s)。

在FERC模型中，当液池前沿位置处的油膜厚度小于某临界值时，流淌火停止蔓延。该临界值可通过重力-表面张力平衡(式3)或重力-粘性力平衡(式4)估算获得：

(3)

(4)

式中：σ为液体燃料的表面张力，N/m；VL为液体燃料的运动粘性系数；hσ，f和hc,f分别为重力-表面张力平衡计算何重力-粘性力平衡计算的油膜厚度，最终的油膜厚度临界值取hσ,f和hc,f最大值。

FERC模型描述了流淌火燃烧面积随时间的变化关系，为进一步分析流淌火灾的危害后果，还需对其热辐射影响范围进行评价。

1.2 火焰辐射模型

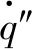
(5)

式中：Ef为火焰表面发射功率，kW/m2；F为目标接收面和固体火焰间的视角系数。对于直径1 m以上的池火，发射率εf和大气透射率τ近似为1[12]。

视角系数的计算由圆柱体火焰的尺寸以及目标接收面与火焰的距离决定，其中圆柱直径为FERC模型计算的流淌火直径。由于池火对外辐射主要来自发光火焰，因此圆柱高度为发光区火焰高度可根据下式计算[13]：

(6)

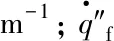
当池火直径大于20 m时，发光火焰区高度不再增大，此最大值表示为[13]：

(7)

由于流淌火燃烧区域面积随时间变化，固定目标接收面与火焰的视角系数也不断变化，因此其接收的辐射热流密度是时间的函数。

1.3 个人风险模型

在定量风险评估中，辐射热流密度值可通过Probit函数转化为个体致死概率，从而计算分析事故工况下的个人风险。个体致死概率表示为[14- 15]：

(8)

式中：u为积分变量；Y为概率变量，可通过人体脆弱性模型计算得到。对于热辐射伤害，概率变量可表示为：

Y=-37.23+2.56ln(q″1.33ts)

(9)

式中：q″为辐射热流密度值，W/m2；ts为暴露时间，s。

2 实例分析

以某长度1 km汽油管道的一段为例。该管道的管径为406 mm，设计压力10 MPa，工作压力6 MPa。汽油的密度为720 kg/m3，有效燃烧热值为 43.7 MJ/kg，汽油的燃烧速率为0.055 kg/(m2·s)[12]，运动粘度系数为0.76×10-6m2/s，表面张力0.022 N/m，最大辐射份数χrmax=0.35，火焰表面发射功率Ef=100 kW/m2，消光系数k=0.05 m-1[13]。

根据美国政府运输部下属的管道及危险物品安全管理局数据库的统计数据，每年成品油管道基础失效频率为1.34×10-3/km[16]。忽略管理、环境等因素的影响，选择该值作为定量风险分析时的失效频率。暂不考虑全管径破裂的情景，假设泄漏孔径尺寸及分布如表1所示。

表1 泄漏孔径及概率分布Table 1 Leak size and the probability distribution

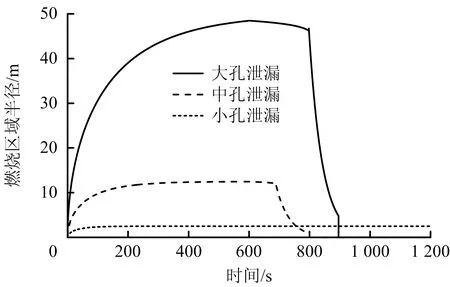
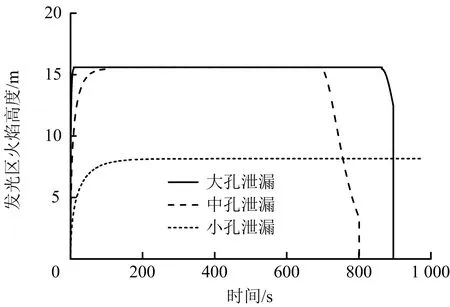
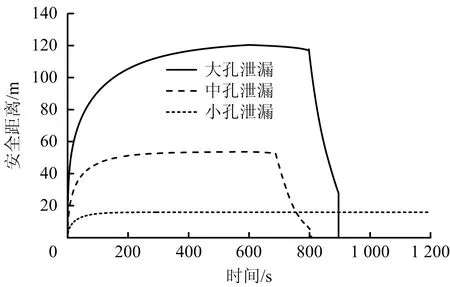
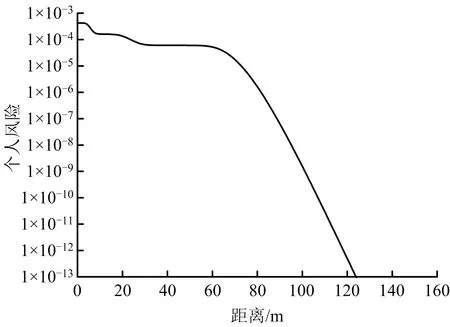
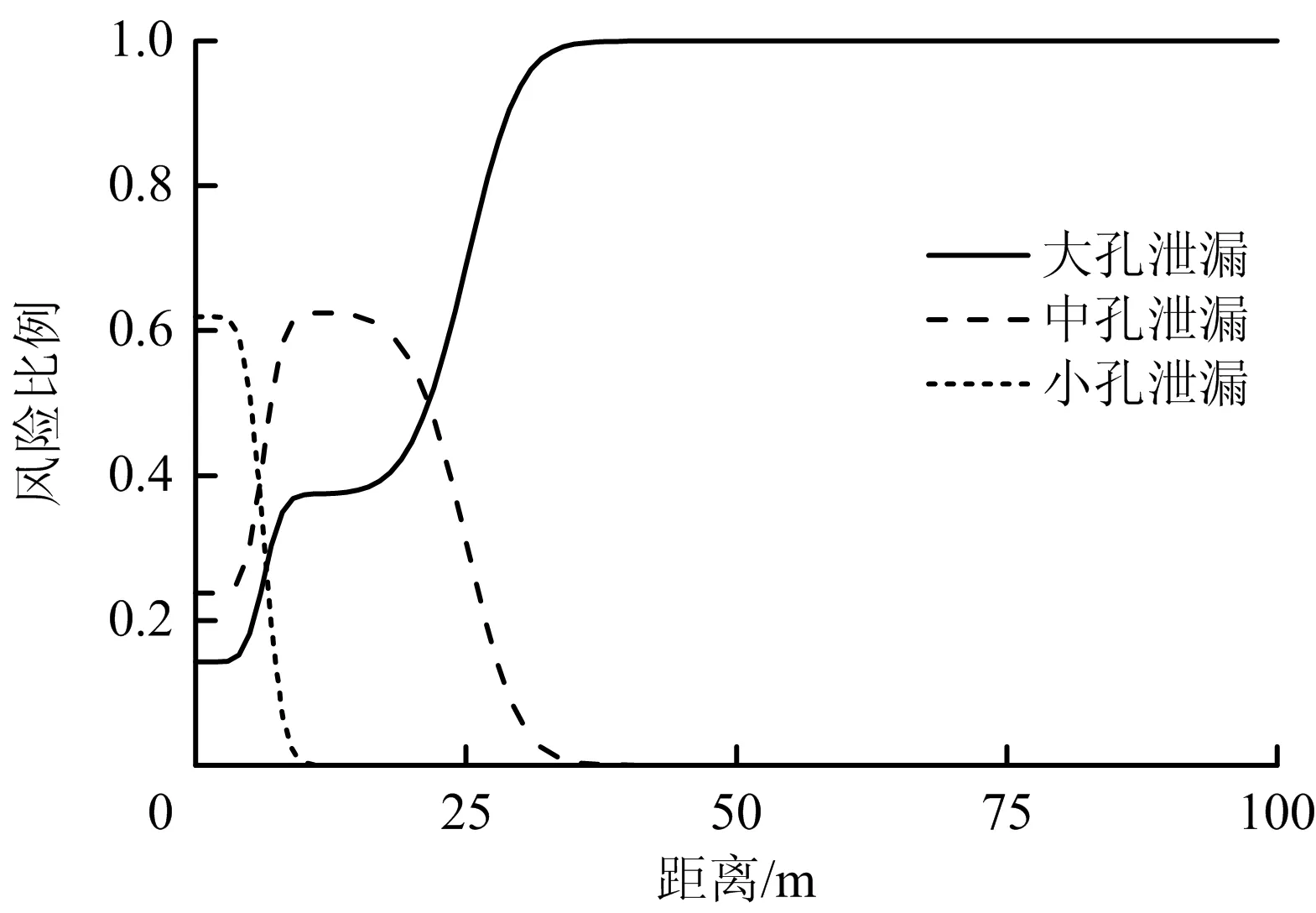
3种不同规模孔径泄漏下，管道隔离关断时间可分别设置为60 ，10和10 min。设定点火概率Pign为0.3。为简化计算，假设汽油一经泄漏即被引燃。如需考虑延迟点燃的情景，仅需在FERC模型中将燃烧速率记作分段函数，即mv=0(t

2.1 泄漏速率

液体经管道上的孔流出，其质量泄漏速率可表示为[15]：

(10)

式中：Ah为泄漏孔大小，m2；Cd为泄漏因数，一般取0.65；P为管道工作压力，Pa；P0为大气压，Pa。

假设泄漏过程中管道压力近似不变。经计算，对于案例中的汽油管道，在小孔、中孔、大孔3种泄漏模式下，其泄漏速率分别为1.17，29.4和470.3 kg/s。

2.2 燃烧面积

将泄漏速率和泄漏时间代入式(1)～(2)所表示的FERC模型微分方程组中，采用有限差分的形式对方程进行离散求解。考虑到液池扩展的停止条件，获得的各工况下即时引燃的流淌火燃烧区域半径随时间的变化曲线如图1所示。

图1 流淌火燃烧区域半径随时间的变化Fig.1 Curves of the time varying radius of the burning pool

由图1可以看出，在管道泄漏初期，流淌火的燃烧区域半径随时间不断增大。初始时，由于液池面积较小，油膜厚度较大，所以液池的扩展速率大。当液池面积逐渐增大后，燃烧消耗量增加，液池中燃料的净增加量减小，液池扩展速率降低。在小孔泄漏和中孔泄漏条件下，出现了流淌火的准稳态燃烧阶段，在该阶段液池半径近似不发生变化。此时，流入液池的泄漏速率和燃烧消耗速率达到动态平衡，FERC模型中质量方程表征的液池体积变化量等于零。在大孔泄漏条件下，流淌火燃烧面积达到稳定值之前管道即隔离关断，因此不存在此动态平衡的过程。

当泄漏时间足够长时，流淌火的燃烧面积与泄漏时间无关，可由泄漏速率与燃烧速率的动态平衡关系进行估计：

(11)

对比3种不同尺寸泄漏情景下的流淌火燃烧区域半径，可以看出，流淌火燃烧面积的最大值随泄漏速率的增加而增大。在小孔泄漏时，燃烧半径仅为2.5 m；在中孔泄漏时该结果增大至12.5 m；在大孔泄漏情景下，流淌火的最大燃烧半径可达48.5 m，相较小孔泄漏增大了18.4倍。

关闭管道截断阀后，由于缺少燃料供应，流淌火逐渐熄灭。由于液池前沿位置处的燃料厚度较低，因此熄灭更早，在视觉上表现为燃烧面积的收缩。在泄漏时间相同的条件下，大孔泄漏条件下流淌火的燃烧时间更长。由于小孔泄漏的关断时间为3 600 s，因此其熄灭过程并未在图1中体现。

2.3 火焰高度

将FERC模型计算的燃烧区域半径代入式(6)中和式(7)中，计算各工况条件下的发光区火焰高度随时间的变化曲线，如图2所示。

图2 流淌火火焰高度随时间的变化Fig.2 Curves of the time varying flame height of the spill fire

当流淌火直径小于20 m时，火焰高度随燃烧面积单调递增，因此对于小孔泄漏，火焰高度随着流淌火蔓延不断增大，直至燃烧面积达到稳定时，火焰高度亦稳定为8.16 m。对于大孔泄漏和中孔泄漏，随着流淌火的蔓延，火焰直径超过20 m，此后火焰高度为15.4 m，不再增大。

2.4 热辐射强度

热辐射强度可根据式(5)所描述的固体火焰模型进行计算，其中视角系数的计算可参考文献[12]。一般将辐射热流密度值小于5 kW/m2的范围视作安全区域。图3为3种不同工况下安全距离的临界范围随时间变化的曲线。小孔泄漏时，流淌火的影响范围较小，安全距离为15.9 m；对于中孔泄漏，安全距离为53.6 m；对于大孔泄漏，流淌火危害影响范围在泄漏后200 s后即达到105 m，此后随着流淌火扩展速率的降低，影响范围增大的速率减小，在泄漏停止时达到最大值120.4 m。相较小孔泄漏，该距离增大了6.57倍。

图3 安全距离随时间的变化Fig.3 Curves of the safe distance of the spill fire

热辐射的空间分布同样是油品火灾评价中较为关注的参数。图4为3种不同工况条件下，当流淌火燃烧面积达到最大值时，辐射热流密度值与空间位置的关系。在距离泄漏点100 m的位置，小孔泄漏、中孔泄漏和大孔泄漏条件下的辐射热流密度值分别为0.13，1.34，8.02 kW/m2，结果差距较大。

图4 流淌火辐射热流密度最大值随距离的变化Fig.4 Curves of the maximum heat flux changing with the distance

2.5 个人风险

通过Probit函数，将各点的辐射热流密度值转化为个人致死概率，并规定在流淌火燃烧区域内，个人致死概率为100%。与泄漏点距离x的位置处，最终的流淌火灾风险可通过下式计算：

(13)

式中：Pi(x)为第i种泄漏情景下x位置处的个人致死概率；Pign为点火概率；Pb为管道泄漏的基础失效概率；fi为第i种情景在泄漏事件中的分布概率。

图5为个人风险分布图。根据《危险化学品重大危险源监督管理暂行规定》[17]，高敏感场所、重要目标和特殊高密度场所的可容许的个人风险标准为3×10-7，居民区、办公区等场所的可容许的个人风险为标准为1×10-6。参考此标准，在本算例假定的失效概率分布条件下，通过FERC模型计算的成品油管道流淌火灾对应的距离分别为85和81 m。

图5 个人风险分布Fig.5 Distribution of individual risk

最终的个人风险综合考虑了3种不同模式的泄漏。就某一种模式而言，其风险值在总的个人风险中所占的比例如图6所示。在距离泄漏点34 m处时，大孔泄漏已经占总的个人风险的99%。因此，在开展风险评价时，应着重分析大孔泄漏的情景。

图6 3种工况在个人风险结果中所占比例Fig.6 The fraction of each case in the total value of individual risk

3 结论

1)流淌火燃烧面积的最大值随泄漏速率的增加而增大，大孔泄漏情景下的最大燃烧半径较小孔泄漏增大了18.4倍。

2)相较小孔泄漏，大孔泄漏下安全距离增大了6.57倍；在距离泄漏点100 m的位置，小孔泄漏、中孔泄漏和大孔泄漏条件下的辐射热流密度值分别为0.13，1.34，8.02 kW/m2。

3)距离泄漏点34 m处时，大孔泄漏已经占总个人风险的99%。因此，在开展风险评价时，应着重分析大孔泄漏的情景。

4)FERC模型能够较好地应用于流淌火灾风险评估。在实际的泄漏情景中，地形特征、风向风速、建筑物等边界条件会对流淌火的蔓延和燃烧产生较大影响，点火时间的概率分布也会影响流淌火的最大燃烧面积。因此，对于精细化的流淌火灾定量风险评价，还需在后续的研究中借助计算流体力学等进行模拟分析并作进一步完善。