空间门限随机前沿模型的构建与估计
蒋青嬗,李毅君
(1.广东外语外贸大学 数学与统计学院,广东 广州 510006;2.中山大学 岭南学院,广东 广州 510275)
一、引言
随机前沿模型是测算技术效率的常用方法,已得到较多理论和实证研究[1-3]。经典的随机前沿模型假定生产函数是线性的,而实际建模会遇到大量非线性问题,因此其应用分析存在局限性。
Hansen首次构建了门限回归模型,为非线性计量分析提供了有效工具[4]。相比于经典的线性模型,门限回归模型存在如下优势:1.考虑了生产单元的异质性,模型更符合实际,适用性更佳;2.样本分割更有效。门限回归模型无需分类回归,可有效地找到合适的外生门限变量或者内生门限变量分割样本。针对随机前沿模型遇到的非线性问题,Tsionas和Tran在门限回归模型的基础上构建了门限随机前沿模型,该模型具有门限回归模型的上述优势[5]。目前关于门限随机前沿模型的理论研究不多,且研究主要侧重在模型构建与估计。如Lee等基于截面数据构建门限随机前沿模型,令技术无效率项服从均匀分布,使用极大似然方法估计模型[6]。Yélou等基于面板数据构建门限随机前沿模型,用大于零的个体截距项指代技术无效率项(此时技术效率非时变),使用最小二乘法估计模型[7]。Mastromarco、Almanidis等分别引入时变技术效率,使用最小二乘法估计模型[8-9]。Lai引入内生门限变量,使用最小二乘法估计模型[10]。Huang和Lai研究了门限随机前沿模型的模型选择[11]。
经典的线性模型和随机前沿模型假定生产单元相互独立,该假定相对严苛。随着空间计量的发展可知,由于地理位置邻近、模仿、溢出效应等原因,相邻生产单元可能存在空间相关性。强制性使用独立性假设会掩盖空间效应。忽略空间效应导致估计量有偏且不一致,技术效率的估计也将不准确。目前空间随机前沿模型有大量理论研究,模型的差别主要体现在空间相关性的引入。空间相关性通过空间滞后项引入到模型,如Kutlu、Glass等在随机前沿模型中引入因变量的空间滞后项[12-13],Hughes、Areal等引入随机误差或者技术无效率项的空间滞后项[14-15]。归纳文献可知目前引入因变量空间滞后项的空间模型应用较广。
本文首次基于空间计量视角拓展门限随机前沿模型,构建空间门限随机前沿模型并估计参数和技术效率。为提高模型适用性,本文同时从技术效率非时变和技术效率时变两个角度进行研究,分别使用两阶段最小二乘法和极大似然法估计参数,使用JLMS法测算技术效率。本文最后进行蒙特卡罗模拟以考察模型的必要性及方法的精度。本文创新之处在于目标模型的适用性较好。首先,空间门限随机前沿模型同时考察了生产单元的异质性和空间相关性,研究内容较丰富。而且目前国内外关于门限随机前沿模型的研究较少,暂无结合了空间计量的研究。其次,本文同时从技术效率非时变和技术效率时变(又含一般时变和特殊时变)两个角度进行研究,充分拓展门限随机前沿模型。再者,本文模型基于面板数据,面板数据包含更丰富的信息量且假设更放松,对应的参数估计和技术效率的估计更准确、可靠。
二、研究设计(一)非时变技术效率空间门限随机前沿模型
基于Yélou等构建的非时变技术效率门限随机前沿模型[9],引入因变量的空间相关性,可构建如下空间门限随机前沿模型:
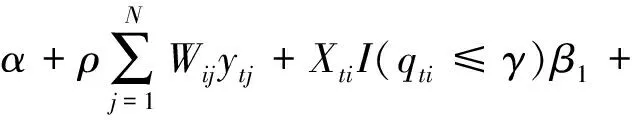
XtiI(qti>γ)β2-ui+vti
(1)
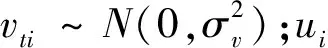
模型(1)基于面板数据,生产单元i在任意时刻的技术无效率项均为ui,相应的技术效率不随时间变化。该模型仅令技术无效率项ui≥0,没有对技术无效率项施加分布限制,适用性相对较好。模型(1)引入因变量的空间滞后项,当ρ=0时模型(1)退化为Yélou等的模型。
模型(1)可简化为:
(2)
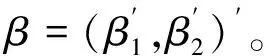
易知,个体截距项为未知。当截面数量趋于无穷时,个体截距项个数也趋于无穷,待估参数个数趋于无穷。模型存在额外参数问题,常用处理方法是,对模型采取一阶差分或者组内变化以消除额外参数,如Wang和Ho、Chen和Schmidt[16-17]。本文采用组内变化消除外参数。
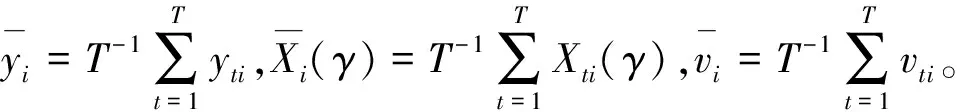
(3)
式(2)减去式(3),有:
(4)
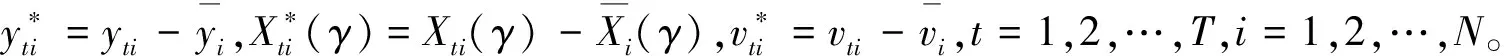
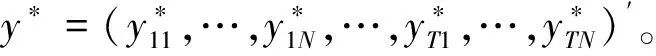
y*=Z*(γ)θ+v*
(5)
模型(5)含内生性问题(源于反向因果),不能如Yélou等使用最小二乘法进行估计。本文采用两阶段最小二乘法(2SLS)估计目标模型。定义变量Q=(X*(γ),(IT⊗W)X*(γ),(IT⊗W2)X*(γ)),该变量可作为(IT⊗W)y*的工具变量,相应的估计量为:
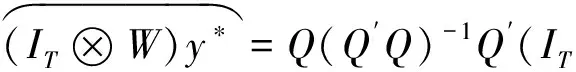
(6)
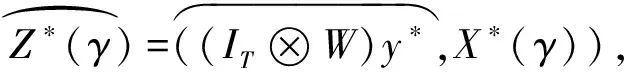
(7)
相应的残差及残差平方和分别为:
(8)
(9)
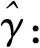
(10)
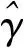
式(10)涉及γ的最优化问题。原则上可用qti,t=1,2,…,T,i=1,2,…,N代替γ并比较似然函数S1(γ)的大小。但该法计算量较大(需计算NT次)且可能导致机制内样本分布不均匀。当样本量较大时,简化方法是:γ仅在qti的η%分位数和(1-η)%分位数范围内取值(本文取η=1),在这段取值内取其{1.00%,1.25%,1.50%,…,99.00%}分位数,针对这393个分位数比较似然函数的大小。简化方法的最优化次数急剧减少且保证了各机制的最小样本量。
(二) 时变技术效率空间门限随机前沿模型
将模型(1)的技术效率拓展为时变,可得如下模型:
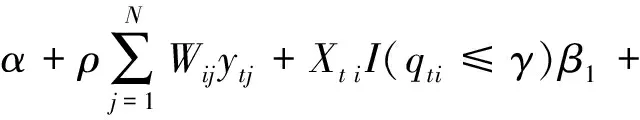
XtiI(qti>γ)β2-uti+vti
(11)
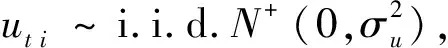
由于竞争、模仿、技术进步等原因,生产单元的技术效率通常随着时间的推移而不断改变。模型(11)中,生产单元i在t时刻的技术无效率项为uti,对应的技术效率随时间变化。模型(11)令技术无效率项服从半正态分布,也可将技术无效率项拓展为服从截尾正态分布、指数分布、伽马分布等,估计步骤与本文类似。模型(11)引入因变量的空间滞后项,当ρ=0时,模型(11)退化为Tsionas和Tran中的模型[7]。
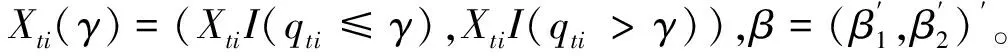
(12)
令y,X(γ),u和v为相应的堆积矩阵,如y=(y11,…,y1N,…,yT1,…,yTN)′。全模型可写成:
y=α1N×T+ρ(IN⊗W)y+X(γ)β-u+v
(13)
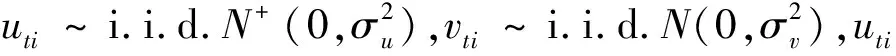
(14)
令复合误差项εti=vti-uti。推导可得复合误差项的密度函数为:
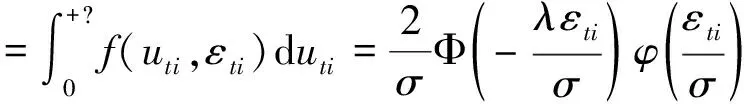
(15)
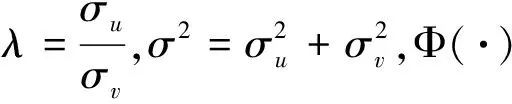
对于给定的门限值γ,其对数似然函数(已去除常数项)可表示为:
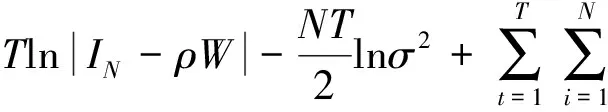
(16)
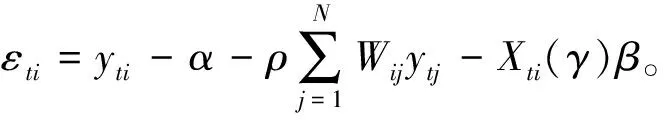
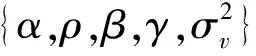
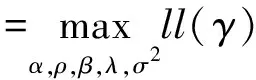
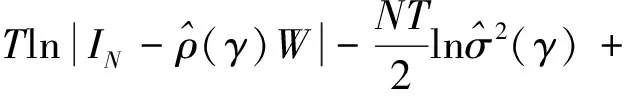
(17)
根据极大似然估计思想,有:
(18)
式(18)涉及γ的多次最优化,同样可采用式(10)提到的简化方法,以减少计算量并保证机制内的最小样本量。对于给定的γ,最优化问题共含p+4个参数{α,ρ,β,λ,σ2}。参数越多,最大化越复杂。令X1(γ)=(1,X(γ)),即X1(γ)为X(γ)左边并上由1构成的单位向量。通过如下变化简化最大化问题:
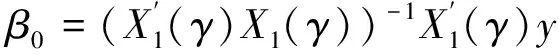
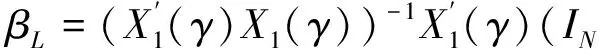
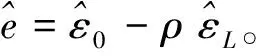
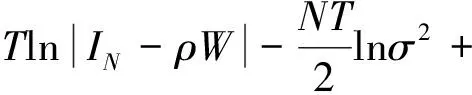
(19)
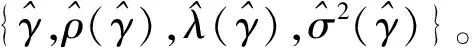
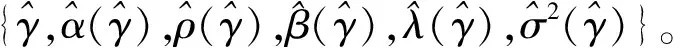
Jondrow等提出的JLMS已成为测算技术效率的主流方法。此处使用JLMS法测算技术效率。推导可得技术无效率项基于复合误差项的条件密度:
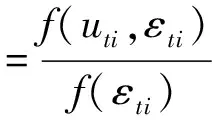
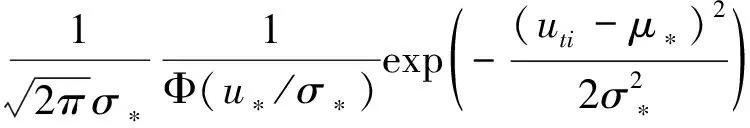
(20)
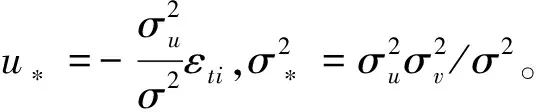
该分布的均值或者众数可作为uti的一个点估计,即:
(21)
(22)
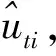
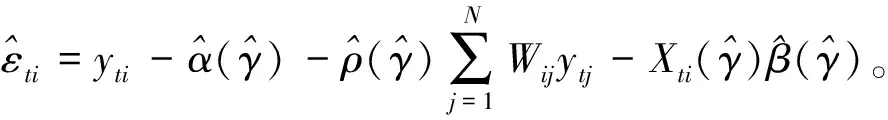
(三)特殊时变技术效率空间门限随机前沿模型
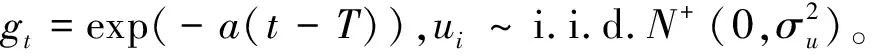
易知复合残差项εti=vti-uti=vti-gtui。令εi=(ε1i,ε2i,…,εTi)′,推导可得εi的密度函数为:
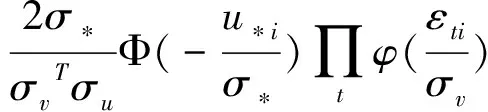
(23)
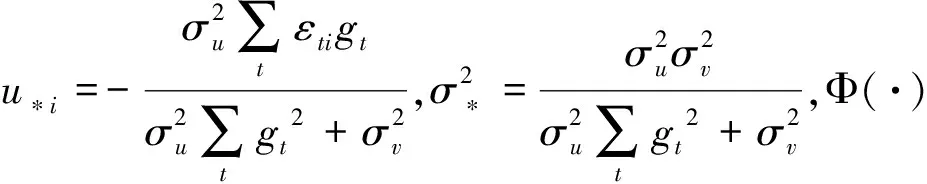
从而对于给定的门限值γ,模型的对数似然函数(去除常数项)可写成:
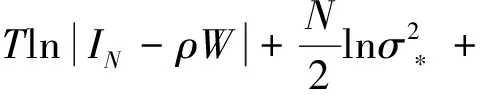
(24)
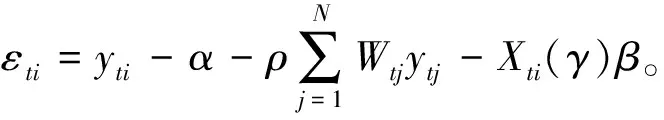
与上节一致,基于极大似然估计思想,有:
(25)
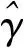
(26)
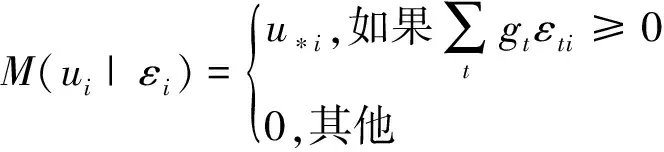
(27)
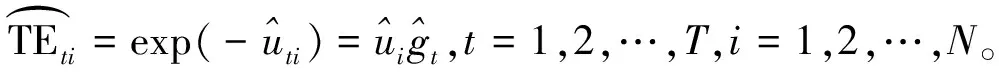
三、蒙特卡罗模拟(一) 模拟设计
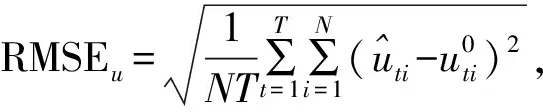
针对时变技术效率门限随机前沿模型,设计如下模拟:
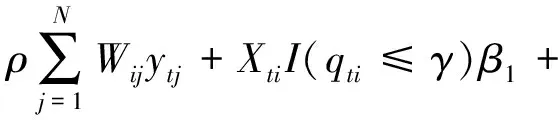
XtiI(qti>γ)β2-uti+vti
(28)
(二) 结果展示
图1展示了技术无效率项估计值与真值的偏离程度。由图1可知,MLE(1)对应箱线图的位置远低于MLE-nS(1)和MLE-nT(1),箱宽远窄于MLE-nS(1)和MLE-nT(1),而且MLE-nS(1)和MLE-nT(1)对应离群值数目较多且数值较大。因此,MLE(1)对应技术无效率项的偏离程度低于MLE-nS(1)和MLE-nT(1),MLE(1)对应技术无效率项的精度远高于MLE-nS(1)和MLE-nT(1)。对比其他两组可得相同结论。综上,MLE对应技术无效率项的估计精度远高于MLE-nS和MLE-nT。现考虑MLE在组(1)~(3)的精度。由图1可知,MLE(1)、MLE(2)和MLE(3)的箱线图位置逐渐降低且箱宽逐渐变窄,从而对应技术无效率项的精度逐步增加,即增加样本容量有助于提高MLE对应技术无效率项的估计精度。
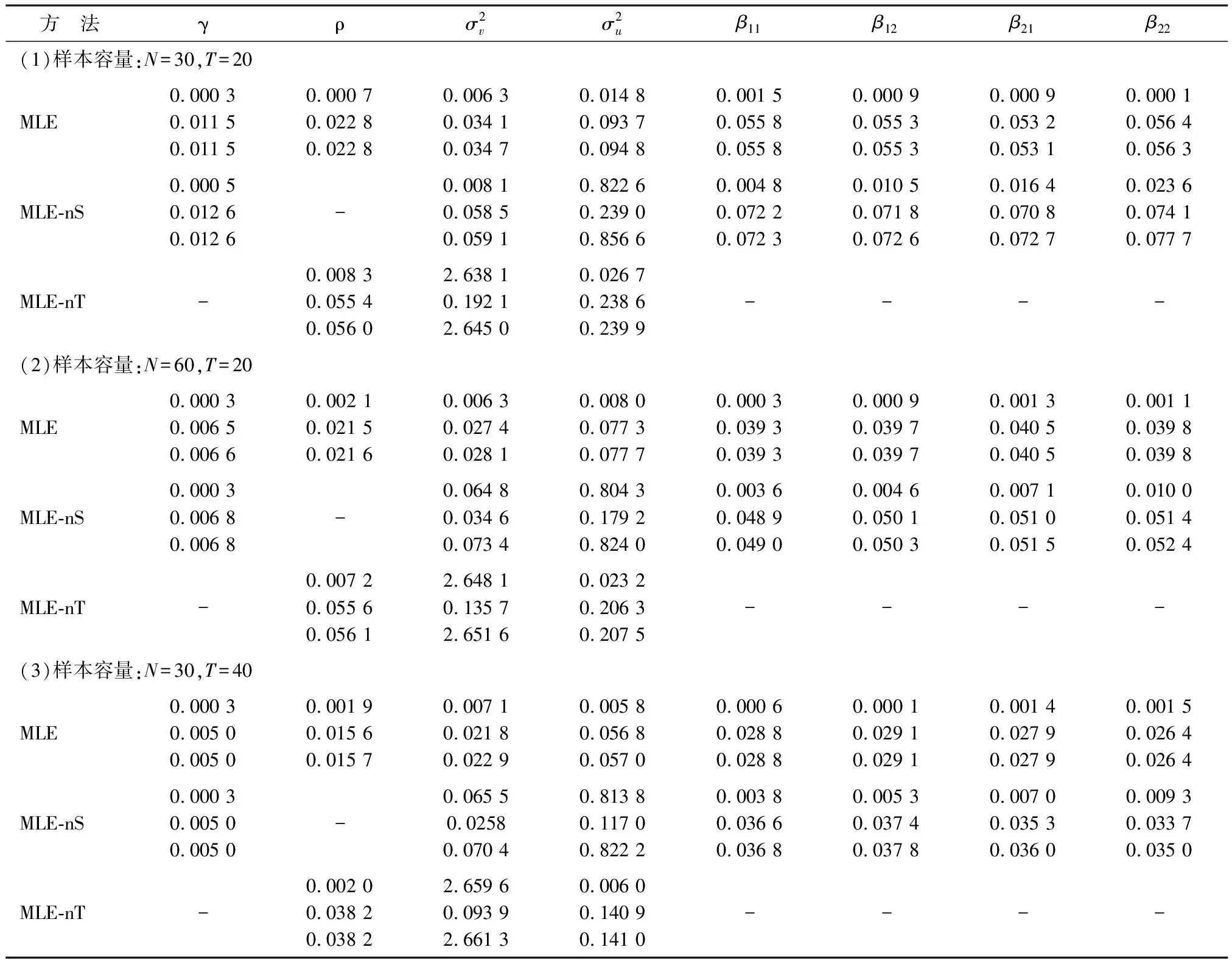
表1 估计量的精度
注:β11和β12为β1对应的两个参数,β21和β22为β2对应的两个参数。结果展示时将偏差、标准差和均方根误差上下排列。“-”表示无对应值。
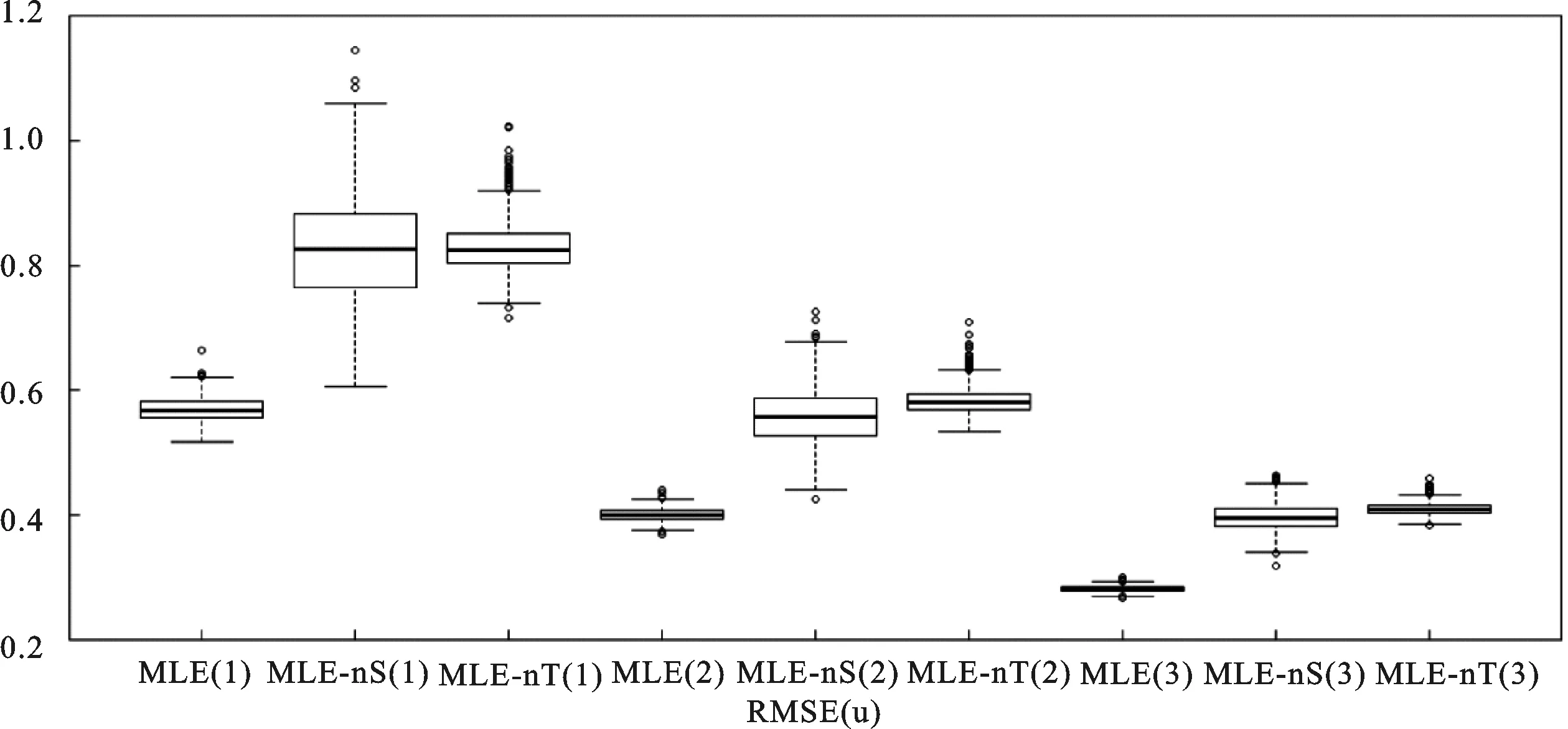
图1 技术无效率项的偏离程度图
注:MLE(1)对应组(1)(即样本容量为N=30,T=20)中MLE对应的箱线图。其他箱线图的命名类似。
四、结论
本文基于空间计量视角,从技术效率非时变和技术效率时变两个角度拓展门限随机前沿模型。模型同时考虑了生产单元的异质性和空间相关性,较符合现实情况且适用性更佳。对于技术效率非时变空间门限随机前沿模型,本文使用两阶段最小二乘法估计参数和技术效率。对于技术效率时变空间门限随机前沿模型,本文使用极大似然估计法估计参数并使用JLMS法测算技术效率。本文最后进行了蒙特卡罗模拟考察模型的必要性和估计方法的精度。模拟结果显示:1.文中方法能有效估计参数和技术效率,而且增加样本容量,参数和技术效率的估计精度均会提高;2.忽略空间相关性或者门限效应,参数和技术效率的估计精度均较低。
上述结果表明,文中模型和估计方法有存在必要性,本文研究较有意义。对于时变技术效率,本文令其服从半正态分布。为提高模型适用性,可将其拓展为服从指数分布或者截尾正态分布,相应估计方法与本文类似。本文使用极大似然方法估计目标模型,当技术效率项的分布稍微复杂时,似然函数的推导非常复杂且最优化可能不收敛或者局部收敛,贝叶斯估计是更合适且更简洁的估计方法。

