基于Hessian矩阵和Gabor滤波的手指静脉特征提取

杨如民，许琳英，余成波

(重庆理工大学 电气与电子工程学院， 重庆 400054)

生物识别是当前炙手可热的人工智能技术的一个重要分支，其中，手指静脉识别系统由于装置简单、检测实时方便、不易伪造等优点而得以广泛应用。然而，当前的手指静脉识别系统由于受光照不均匀[1]、个体组织差异如手指厚度差异[2]等因素的影响，采集到的静脉图像模糊、对比度低、质量较差、严重影响静脉识别的可靠性。

为了解决这一问题，国内外学者对提高静脉识别性能的方法进行了大量研究，例如，Pi等[2]把边缘保护滤波器，椭圆高斯滤波器和直方图均衡化相结合增强静脉图像的对比度。Yang等[3]提出了基于恢复的增强方法，消除相机的光学模糊和手指结构中静脉的光学散射模糊。然而，该方法不能正确估计出静脉区域皮肤表面的深度，且耗费大量的处理时间。Park等[4]提出基于Gabor滤波的利用手指静脉的方向和粗细增强图像，然而两步式的Gabor滤波器的使用耗费大量的运算时间。Lee等[5]提出了基于皮肤散射和光学散射的手指静脉恢复方法，在一定程度上解决了由于皮肤表面不良所造成的图像模糊，但是未考虑手指静脉组织造成的图像模糊。余成波等[6]提出了使用多阈值的模糊增强方法，不同于传统的模糊阈值增强方法，利用了图像的局部信息进行图像消模糊。Cho等[7]提出基于检测静脉方向和宽度的自适应Gabor滤波增强算法，用线性追踪进行线检测，追踪静脉的方向，然而图像的性能会随着方向和宽度的检测不准确而下降。Hessian矩阵的特征值通常用于血管增强，因为在医学图像中，它们可以用来增强图像中的线性结构[8]。Jerman[9]提出了基于Hessian矩阵特征值的多尺度增强算法，对医学血管图像进行增强。林剑[10]提出基于Hessian矩阵的手指静脉图像分割方法，但未进行特征提取和算法的可行性验证。Miura等[11]开创性的提出了重复线性跟踪的静脉特征提取算法，但该算法受预先设置的参数和迭代次数影响较大，在参数设置不当时，易造成静脉特征点的漏检。文献[12]提出了一种鲁棒的特征提取方法，通过计算静脉横截面局部最大曲率提取静脉的中心线，然而该方法旨在精准定位静脉并未进行图像增强，易受噪声影响，对于低质量的图像不适用。M.Vlachos[13]提出基于统计特性的二次区域生长算法对手指静脉进行特征提取，同样，也未进行图像增强处理，因而易受噪声影响，不适用于低质量的图像的特征提取。

综上所述，图像特征的提取是提高识别性能的关键，而在提取静脉特征之前，对图像进行增强处理、提升图像质量，又是改善特征提取算法的重要手段。因而，本文提出基于Hessian矩阵特征值比率(Ratio of eigenvalues，简称ROE)的增强算法和改进的Gabor滤波特征提取算法相结合的手指静脉特征提取算法，实验表明，在一定程度上克服了以上方法的不足，改善了识别性能。

1 手指静脉图像预处理

由于手指放置在采集器上的方位影响，导致采集的手指静脉图像产生平移、旋转、漏光引起的低对比度现象，从而不能较好的提取出静脉特征。因此，采集的图像要先进行预处理，主要包括：(i)分割出感兴趣区域(ROI)(ii)图像的平移和旋转矫正。

手指静脉图像通过阈值粗略的定位图像中手指的形状，获得二值图像。然后通过sobel边缘检测提取手指轮廓。通过二值图像与边缘图的差值得到手指静脉区域的大致二值图像。再经过形态学操作得到二值掩膜图像，掩膜图像与原图像相乘即得到感兴趣区域。

由于采集时，受测者手指摆放位置的偏差，影响后续的匹配识别的性能。因此获得图像感兴趣区域后，需要进行平移和旋转矫正。图像的Hu矩是一种具有平移、旋转和尺度不变性的图像特征。因此采用Hu矩对图像进行旋转矫正，采用仿射变换进行平移矫正。

图1为手指静脉预处理的部分流程。

图1 手指静脉预处理不同阶段

2 基于Hessian矩阵的增强算法

图像增强是对低对比度静脉图像特征提取的关键，增强静脉纹路，为后续的特征提取做准备。基于Hessian矩阵的结构图像滤波器被广泛应用于血管类图像增强，处理方法是对Hessian矩阵的特征值分析。Hessian矩阵是由图像的水平、垂直、对角的二阶偏导构成。Hessian矩阵的特征值估计可以用来确定区域内出现静脉血管的概率。

(1)

fxx，fxy，fyx，fyy为二维图像的四个二阶偏导数。f(x,y)为当前像素灰度值，f(x±1,y±1)为f(x,y)3×3邻域像素灰度值。

水平方向的二阶偏微分：

(2)

垂直方向的二阶偏微分：

(3)

对角方向的二阶偏微分：

f(x,y)-f(x+1,y)-f(x,y+1)

(4)

可以用λ1，λ2构造增强滤波器，在二维图像中，Hessian矩阵的计算公式为：

(5)

静脉血管的形状、前景和背景亮度可以通过分析Hessian矩阵的特征值的符号和大小进行判断。二维图像中，线状的静脉的特征值关系为|λ1|<|λ2|,λ2的符号正(负)表示在亮(暗)背景上，静脉是暗(亮)。即：

由于Hessian矩阵的最大特征值和特征向量对应最大曲率的的强度和方向，反之亦然。静脉结构沿剖面方向曲率最大，沿静脉方向曲率最小，噪声点沿各方向曲率都大，背景灰度变化小曲率几乎为零。所以特征值与图像像素点的关系如表1。

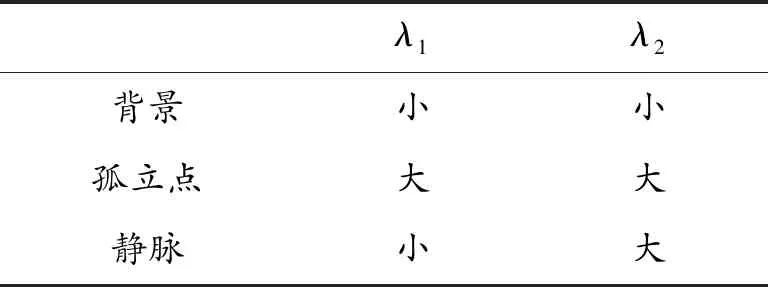
表1 特征值与图像像素点的关系

为了增强不同尺寸的静脉结构，通常在高斯尺度空间上进行分析图像。用f(x,y)表示N维图像在坐标(x,y)处的灰度，每一个像素在(x,y)处和尺度σ的二阶偏导数来构造的Hessian矩阵：

(6)

由于基于Hessian矩阵的Frangi二维血管检测的增强函数与特征值的平方成正比，主要是抑制低对比度，不均匀区域的噪声，这些区域特征值较小。而实际静脉血管特征值并不均匀，特征值在静脉中心达到最大值，沿着截面方向至边缘逐渐减小，对静脉交叉点和弯曲处响应较差,且低对比度的静脉图像灰度变化不明显。针对此缺陷，文献[14]针对三维医学图像提出了基于特征值的增强函数，用于椭球型扩散张量的检测，不再与特征值成比例。λ1，λ2，λ3为三维图像Hessian矩阵特征值。在文献[15]中，λ1为平行于组织结构的扩散系数，λ2、λ3为组织横截面的扩散系数。最直观最简单的旋转不变指数为扩散率的比值为：

(7)

文献[14]对λ3归一化处理为：

(8)

文献[14]的增强函数为：

(9)

为了确保增强函数对低特征值的鲁棒性，本文对λρ的归一化区间进行一些改进。本文主要针对二维灰度图像，且是亮背景上暗静脉结构，故令λ2=λ3，λ2为正，因此通过maxλ2(x,σ)获得大的λ2值来增强低对比度的静脉结构。故

(10)

本文所提的增强函数为

(11)

τ是取值区间在(0,1)内的阈值，λρ是通过不同尺度σ计算得到的。低对比度的静脉结构，其特征值较小，易受低对比度中噪声的影响，选择较大的τ值，会扩大λ2和λρ大小差，从而增强静脉结构。

3 基于差值Gabor滤波的特征提取

Gabor滤波器对图像的平移和旋转较鲁棒，纹理特征提取能力显著，被广泛用于提取图像中的纹理方向信息[16]。本文采用Gabor滤波器提取手指的静脉特征。但是由于采集设备的影响，采集的静脉图片噪声较多。因此对Gabor滤波器加以改进，提升特征提取性能。

二维Gabor滤波器是一个正弦波和高斯核函数的乘积，实际上就是一个高斯核和正弦波调制的结果。Gabor滤波器的定义为：

Gσ,μ,θ(x,y)=gσ(x,y)·exp[2πjμ(xcosθ+ysinθ)]

(12)

j=√-1，gσ(x,y)为高斯包络，定义如下：

(13)

σx，σy为高斯函数标准差，μ是调谐函数的标准差，θ为滤波器的并行条纹的方向，使用欧拉公式，Gσ,μ,θ(x,y)可以分解为一个实部Rσ,μ,θ(x,y)和一个虚部Iσ,μ,θ(x,y)。实部适合对手指静脉图像进行脊检测，虚部适合进行边缘检测。

Gσ,μ,θ(x,y)=Rσ,μ,θ(x,y)+j·Iσ,μ,θ(x,y)

(14)

Rσ,μ,θ(x,y)=gσ(x,y)·cos[2πμ(xcosθ+ysinθ)]

(15)

Iσ,μ,θ(x,y)=gσ(x,y)·sin[2πμ(xcosθ+ysinθ)]

(16)

二维Gabor滤波器对不均匀光照区域会有轻微的响应，被称为直流分量，为了使Gabor滤波器对光照鲁棒，因此消除直流分量。

(17)

(2k+1)2为滤波器的尺寸。因此对光照鲁棒的Gabor变换定义如下，

(18)

I(x,y)表示静脉图像，⊗代表卷积操作。手指静脉有不同的方向，如水平、垂直、对角。因此，Gabor滤波器选择八个方向：0，22.5°，45°，67.5°，90°，112.5°，145°，167.5°。由于采集设备光照的影响、采集者静脉天生模糊不清等因素造成采集的图像对比度较低，受噪声影响较大。

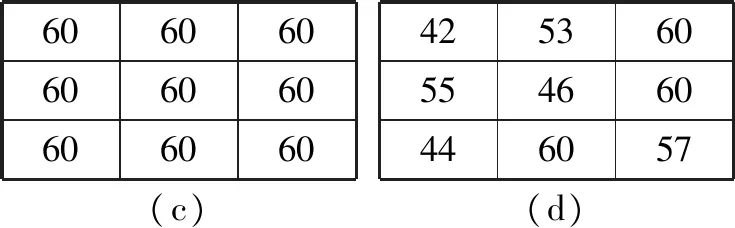
图2给出了几种灰度模式，图2(a)灰度变化明显，图2(b)为一个噪声点，图2(c)灰度无变化，图2(d)灰度缓慢变化。静脉灰度基本呈现谷形分布，较静脉两侧灰度低。图2(a)大体是静脉灰度分布，Gabor滤波在水平方向响应最大，垂直方向响应最小。图2(b)和图2(c)在各个方向响应大小相同，图2(d)各个方向响应大体一样，图2(b)、图2(c)、图2(d)三幅图滤波差值接近为0，图2(a)图差值最大。因此本文提出差值Gabor滤波增强的特征提取算法，相位差值为90°，减弱噪声的影响，提高特征提取的鲁棒性。

15015015080808015015015015015015015080150150150150(a)(b)

606060606060606060425360554660446057(c)(d)

图2 四种灰度模式

因此对噪声鲁棒的Gabor变换的定义如下：

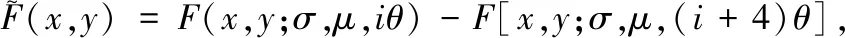
i=1,2,3,4

(19)

所提算法流程：

输入:手指静脉图像输出:提取的二值静脉特征图像(1)预处理,提取出手指区域,并进行旋转平移矫正,获得矫正图。(2)利用公式计算特征值,并根据增强函数计算增强值,获得静脉增强图。(3)增强图作为输入,根据公式计算八个方向的静脉特征,获得静脉特征图。(4)将相位差为90°的特征图做差,得到差值Gabor特征图。(5)对特征图进行二值化并进行形态学后处理,得最终提取的二值静脉特征图像

图3为手指静脉特征提取流程：

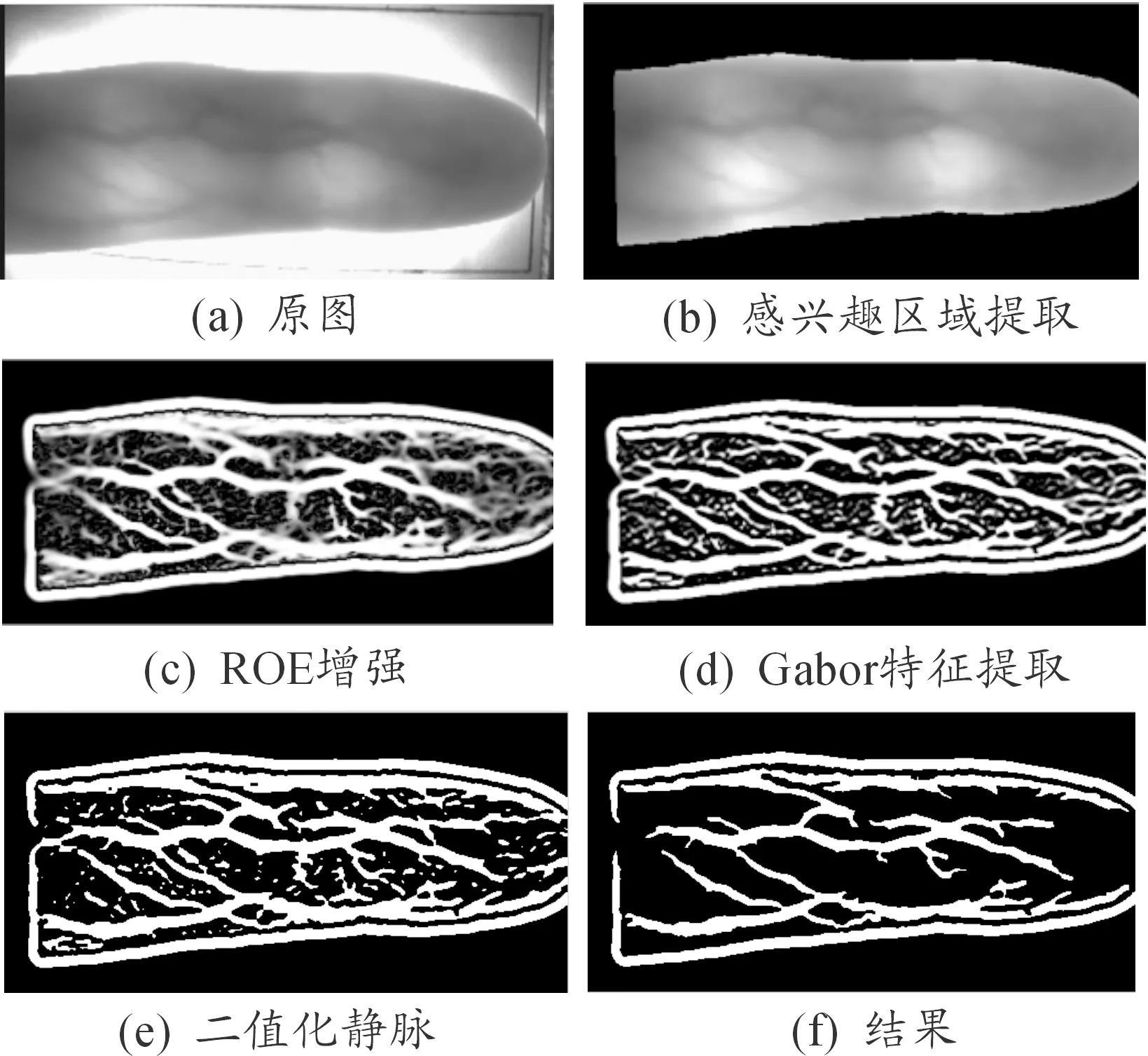
图3 手指静脉特征提取流程

4 实验结果及性能分析

4.1 参数设置

本文所用的增强算法，为使尺度因子σ尽可能接近静脉的宽度，使用枚举法把范围限定在[0.5,3]，步长为0.5，根据增强函数的响应选择出最接近静脉的尺度因子。τ值一般取值为0～1，τ值较大只对较粗的静脉有增强效果，τ值较小时才能兼顾细小静脉的增强。经过多次试验，当τ=0.15时增强效果最好。图像增强结果如图3(f)、图4(d)和图5(d)所示，与原图相比，构造的滤波器增强函数对细小的静脉结构也能有效的增强。基于Gabor差值的特征提取算法中，Gabor核函数方向θ取值为[0,11π/12]，步长为π/12，σx=8，σy=2，正弦函数频率μ=0.1。

4.2 结果分析

本文与以往比较经典的两种特征提取算法进行比较，分别是最大曲率法和重复线性跟踪法。主观上直接观察图像特征提取效果，如图4、图5所示：最大曲率法效果最差，由于低对比度的手指静脉的灰度分布并不是非常明显的谷形，导致静脉漏检，效果较差。重复线性跟踪法受预先设置的参数和迭代次数影响较大，且易受噪声的影响，产生伪静脉。在本文实验迭代的次数为1 000次，仍有部分细小的静脉特征漏检，且运算效率低。本文所提的方法主观上看，静脉的主体结构和细小的结构都可以有效的提取。

图4 含细小静脉的特征提取

图5 低对比度手指静脉特征提取

客观上通常用等误率(EER)验证所提算法的有效性，即手指静脉类间匹配的错误接受率(FAR)等于类内匹配的错误拒绝率(FRR)。三种算法误识率、拒识率如表2、表3所示：图6为ROC曲线，曲线越接近横轴即说明正确率越高，算法性能越好。

表2 1∶1验证结果

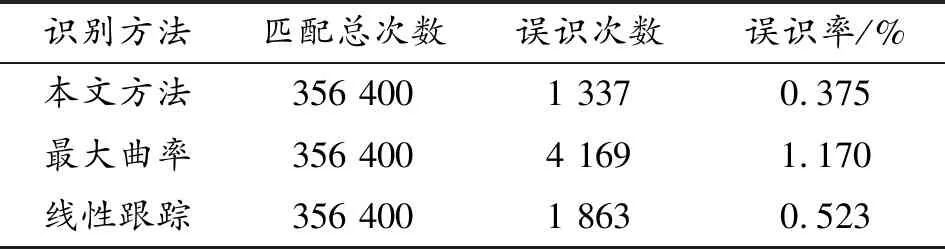
表3 1∶n验证结果

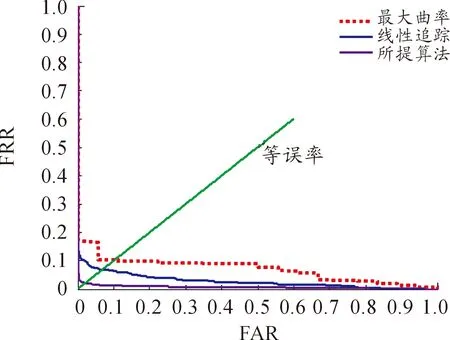
图6 三种匹配算法的ROC曲线

由图6可知，本算法验证模式下的等误率为2.1%，重复线性跟踪法和最大曲率法等误率为7.01%和10.26%，由表2、表3可知，本文算法的FAR为0.375%，FRR为1.73%，综上所述本算法优于其他两种算法。

5 结论

1) 本文用Hessian矩阵和Gabor滤波相结合，构造了基于Hessian矩阵的特征值比率的增强算法对静脉进行增强，然后利用差值Gabor滤波进行特征提取，提出了一种新的手指静脉特征提取算法。

2) 在PolyU手指静脉数据库的实验表明，相比较其他静脉特征提取方法，所提方法对手指静脉特征提取的更加充分，比目前其他的手指静脉提取算法的识别性能有所提高。