空心钨球孔腔直径对靶板侵彻能力的影响

程 瑶，王春光，杨宝良，杨 丽，张 银，赵太勇，陈智刚

(1.中北大学机电工程学院， 太原 030051; 2.晋西工业集团有限责任公司 防务装备研究院， 太原 030051; 3.西安现代控制技术研究所， 西安 710065; 4.中北大学 地下目标毁伤技术国防重点学科实验室， 太原 030051)

钨球破片因其强度大，密度大，高比动能以及毁伤效果明显等特点，已经广泛应用于多种预制破片弹中，这种在战斗部上装填钨球预制破片，极大地提高了战斗部的毁伤能力，是提高其威力的重要途径。为了适应现代武器战斗部发展的需求，国内外学者对球形预制破片的毁伤能力，以及如何提高战斗部的杀伤威力问题做了许多理论与实验研究。李明星等对不同形状轴向预制破片的飞散特性进行了研究，得到了球形预制破片的飞散角最大[1]；张国伟等研究了提高杀伤战斗部威力的途径，并得出重金属钨破片具有非常优越的侵彻性能[2]；贾光辉等对钨破片进行极限贯穿实验，得到球形钨破片侵彻性能优于球形钢破片[3]；贾光辉等研究了钨球垂直侵彻薄钢靶，在极限穿透条件下靶板发生开坑和冲塞，且钨球发生巨大变形[4]；张国伟等研究了不同质量钨球侵彻不同厚度钢靶，在限极贯穿速度下的钨球变形规律[5]；贾光辉等通过钨球垂直侵彻钢靶试验，得到各种弹靶条件下的极限贯穿速度，且经计算分析，得出钨球侵彻钢靶过程中的能量分配规律[6]；康爱花等研究了弹道极限速度对装甲钢抗弹性能的影响，并推导出弹道极限穿透速度的计算公式[7]；裴思行等研究了钨球垂直侵彻多层间隔靶，研究其侵彻机理，并建立了相应的理论计算模型[8]；赵晓旭等建立了钨球高速侵彻低碳钢板成坑直径的计算模型[9]。

本文从钨球预制破片出发，研究带有不同孔径的空心钨球垂直侵彻钢靶的仿真模拟，对比各孔腔半径与钨球半径比下的钨球侵彻效能，得出最优配比，为空心钨球的结构设计提供理论指导。

1 数值模拟

数值建模上为节约时间，采用1/4结构建立三维有限元模型，并且设置对称约束条件在1/4模型的对称面上，计算网格部分均采用Solid164八节点六面体单元，各PART之间均采用Lagrange算法。并且在模型的边界点上施加压力流出边界条件，避免压力在边界上的反射。整体模型由空心钨球和6 mm钢靶两部分组成。其中空心钨球直径分别为4.5 mm、5 mm、5.5 mm、6 mm、6.5 mm，每一种空心钨球都有0 mm(实心)、0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm、4 mm九种不同的孔腔直径。整体模型如图1所示。

图1 空心钨球侵彻钢靶整体模型

在穿甲过程中考虑到作用时间短，应变率高及高温高压下金属材料的塑性流变。钨合金破片和钢靶采用JOHNSON-COOK热黏塑性本构模型和GRUNEISEN状态方程[10]。各材料主要参数如表1所示。

表1 材料模型主要参数

2 数值模拟结果与分析

2.1 仿真过程分析

在空心钨球侵彻靶板的过程中，孔腔半径r与钨球半径R之比不同，侵彻过程中钨球的形变与侵彻能力均不同。若忽略材料内部横波的传播，将弹性波和塑性波等效为冲击波，钨球刚着靶时，在其接触面会受到应力波的作用，高速冲击的瞬间，钨球会产生背向冲击面的冲击波，此时钨球被压缩，压缩波以球形波的形式传播，在两侧自由面反射向钨球内部传播，与靶板在冲击面反射回来的拉伸波同时向钨球内部传播，当压缩波传播到空腔时，被空腔自由表面反射，该反射波与靶板冲击面上的反射波叠加，在波与波相遇处钨球可能会产生破裂，当压缩波穿过空腔到达另一自由面反射后，反射后的拉伸波与背向冲击面的冲击波共同作用，在轴向上，钨球顶部自由面产生轴向拉伸塑性应变；在径向上，由于压缩波在两侧的反射波遇空腔后再次反射和由空腔反射的反射波一起沿径向向中心轴线汇聚，使钨球发生径向塑性拉伸变形，钨球径向膨胀增大。如表2所示，在可以贯穿靶板的情况下，随着空心钨球孔腔半径的增大，侵彻靶板的初始速度增大，钨球在侵彻靶板时自身轴向压缩变形变大，径向拉伸变形增大，贯穿靶板孔径比实心钨球大，当孔腔半径与钨球半径比大于0.8时，在侵彻过程中钨球破裂严重，失去侵彻能力。总体来说，空心钨球较实心钨球质量小，爆炸赋予钨球的初始能量一定，空心钨球较实心钨球速度高，侵彻能力强，而当空腔比大于0.8时，钨球无侵彻能力。

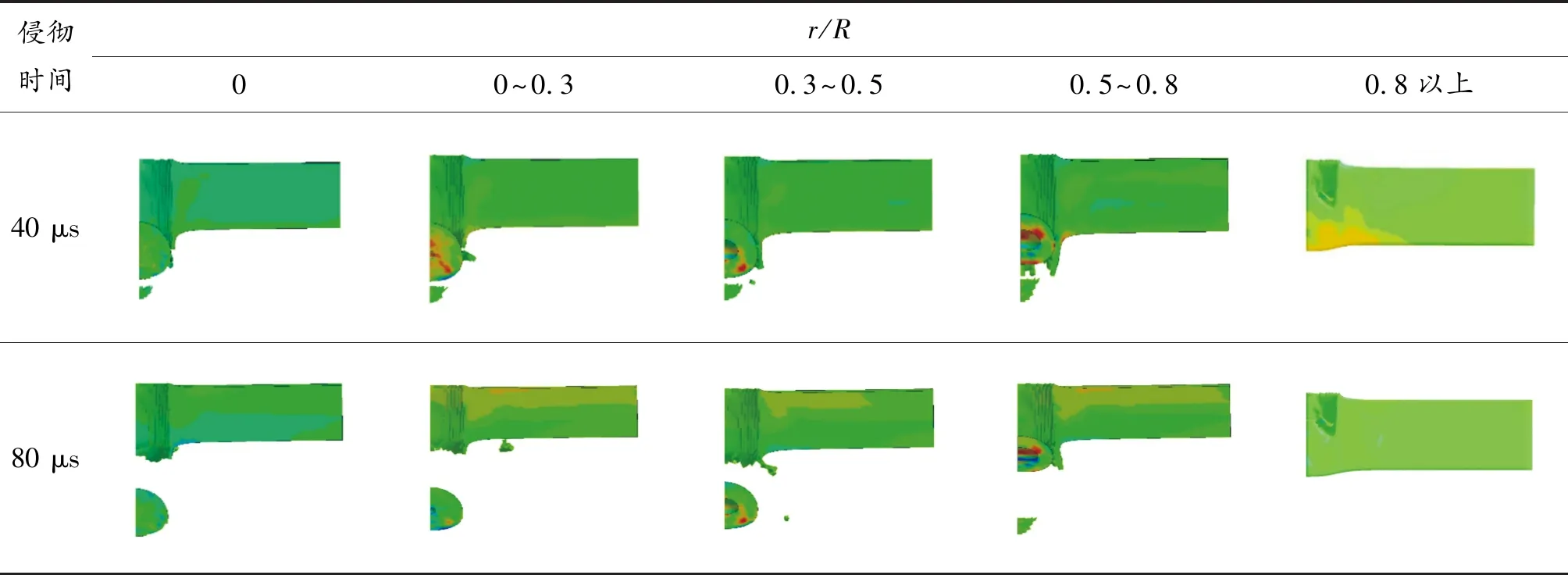
表2 不同r/R空心钨球侵彻靶板

2.2 数值模拟结果分析

如图2所示，仿真模拟了不同半径钨球侵彻6 mm靶板时的剩余速度随孔腔半径与钨球半径比的增大而变化的图像。由图像可以看出，随着孔腔半径与钨球半径比r/R的增大，不同半径的钨球余速都表现出先增大后减小的趋势，直到增大到一定比值后不能贯穿靶板，即余速为零。在计算余速之前，通过仿真计算得到不同直径钨球在不同大小孔腔下的极限穿透速度[11]，随着孔腔半径比的增大，应力波在空腔表面的反射，削弱了沿侵彻方向的应力波，且钨球径向变形较大，使着靶面积增大，极限穿透速度增加。由于弹丸爆炸后给予破片的初始能量一定，根据极限穿透速度，赋予钨球合适的初始速度，质量小的钨球在侵彻过程中具有较大的速度，相同r/R下的余速也比较大，由图可知，实心钨球的余速普遍小于一定比例的空心钨球，当r/R在0～0.3左右时，不同大小的钨球均具有较高的余速。

图2 钨球余速-r/R变化曲线

由图3可以看出，不同半径的钨球侵彻靶板的剩余能量随着r/R的增大而先增大后减小直到不能贯穿靶板，当孔腔半径与钨球半径比在0～0.3左右时，钨球的剩余动能最大。由于弹丸爆炸后给予破片的初始能量一定，说明在此范围内钨球的能量损失最小，侵彻能力最强。

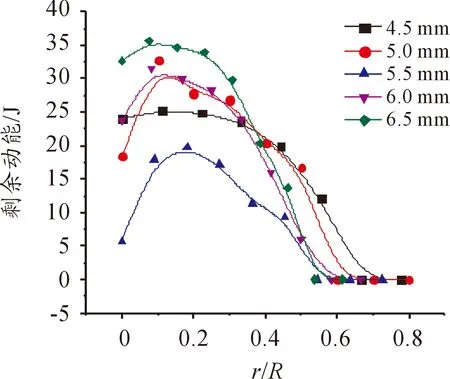
图3 剩余动能-r/R变化曲线

由图4和图5两图可以看出，同一种半径钨球，随着中间孔径的增大，入孔和出孔半径随之增大，当空心比增大，碰撞受到应力波时，中间空心部分受力易变形，孔径越大，变形越大，在侵彻靶板过程中，贯穿孔径也随之增大，而实心钨球变形最小，其贯穿孔也最小。相同r/R下，钨球半径越大，孔径也越大，由两图可以看出，随着钨球半径的增大，空心孔径在增大，钨球侵彻变形越大，出入孔半径增大。在侵彻相同靶板时，空心钨球的侵彻毁伤效果比实心钨球强。

图4 入孔直径-r/R变化曲线

图5 出孔直径-r/R变化曲线

3 结论

空心钨球较实心钨球有更好的侵彻能力。当空心孔腔半径与钨球半径比在0～0.3时，钨球剩余速度最大、残余动能最大以及贯穿孔径比实心钨球大，侵彻效果更佳；当孔腔半径与钨球半径比大于0.8时，钨球破裂严重，质量损失较大，几乎没有侵彻能力。当钨球直径一定时，可方便地计算出该直径下侵彻能力最好的空心钨球的孔腔半径，为提高钨球预制破片的毁伤效能提供了一定的参考价值。