基于MFCC与GFCC混合特征参数的说话人识别

周 萍，沈 昊，郑凯鹏

桂林电子科技大学电子工程与自动化学院，广西桂林541004

说话人识别技术作为多种生物认证技术之一已经广泛应用于社会生活中的多个领域，相比于其他识别技术，该技术有着语音信息采集方便且不易遗失的优点.说话人识别本质上是一个模式识别的问题，因此识别之前如何提取出具有表征说话人唯一特性的参数就成了这一研究的热门话题，也随之涌现了许多提取特征参数的方法.目前，最常见的特征参数有基音周期、共振峰、线性预测倒谱系数(linear prediction cepstral coefficient,LPCC)、Mel 频率倒谱系数(Mel frequency cepstral coefficient,MFCC)等[1]，但这些方法所提取的特征参数有一定缺陷，且单一特征参数无法完全表征说话人的所有特点，于是出现了将不同特征相互融合的改进算法，在一定程度上提高了特征的有效性和识别率[2-4].最常用的Mel倒谱系数是根据人耳结构设计的三角滤波器组进行特征提取的，但在噪声情况下的识别效果急剧下降.Gammatone 函数最早由Johannesma 提出，能够精确模拟人耳的听觉响应，且具有较强的噪声鲁棒性[5-7].文献[8]考虑到不同特征参数的各个特征分量对识别结果的贡献不同，将所有特征参数进行简单混合，但维数过高以致影响识别效率.为了获取更完善的特征参数，滤除干扰因素，本文采用增减分量法剔除贡献度较低的维度，然后将Mel 频率倒谱系数和Gamma 频率倒谱系数以及它们的差分倒谱系数进行有效的混合，以替代单一的倒谱系数作为说话人声纹识别的特征参数，最后采用高斯混合模型(Gaussian mixture model,GMM)识别混合倒谱参数.实验表明，本文方法提取的混合特征参数MFCC+∆MFCC+GFCC+∆GFCC 更能体现说话人的特征，有效提高了识别率.

1 MFCC 和GFCC 及其一阶差分特征参数提取

人类能够正确地分辨出说话人声音的不同，是因为人耳的听觉系统具有很高的复杂度.要使机器正确区分说话人，必须对说话人的声纹进行特征提取，使之成为机器可以区分的特征参数.MFCC 和GFCC 都是根据人耳的特征结构而提出的特征参数，因此在特征提取方面具有优势.

1.1 Mel 特征参数提取

人耳的听觉与频率成非线性关系，频率与Mel 频率之间的关系可以近似表示为

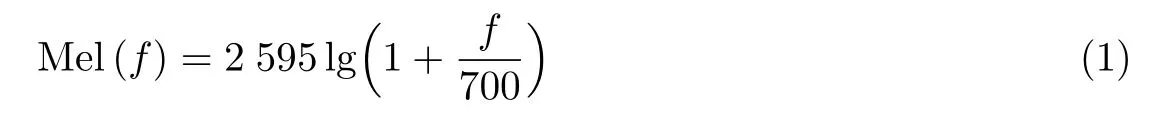
MFCC 以人耳特性设计的一系列非线性的Mel 三角滤波器对语谱信号进行滤波，然后进行离散余弦变换，最后进行倒谱变换就可以得到MFCC 特征参数.MFCC 特征参数的提取过程如图1所示.

图1 MFCC 的提取过程Figure1 Extraction process for MFCC

语音信号预处理阶段主要包括预加重、分帧、加窗、端点检测、去噪处理等过程.经预处理得到信号xi，再通过快速傅里叶变换使数据从时域转换到频域，得到频谱上的能量分布X(i,k)，取其模的平方得到谱线能量E(i,k)；然后送入26 维（本文算法取26 维时效果最佳）的Mel 滤波器组，计算出在Mel 滤波器的能量，并取每个滤波器输出的对数能量S(m)；最后根据式(2)进行DCT 变换，得到MFCC 特征参数

式中，Cn为特征参数，M为滤波器的数目.

MFCC 主要提取的是语音的静态特征.为了满足人耳的构造特征，凸显语音信号的动态变化，通常对特征参数进行二次提取.本文选用∆MFCC，即MFCC 的一阶差分，差分之后得到特征参数表达式如下：

式中，k取2，即以第t帧的前后各2 帧MFCC 参数变化来反映当前帧的动态特性.

1.2 GFCC 特征参数提取

Gammatone 滤波器是一种基于标准耳蜗结构的滤波器，其时域表达式如下：

式中，A为滤波器的增益；fi为滤波器的中心频率；U(t)为阶跃函数；φi为偏移相位，而人耳对相位偏移不敏感，因此为了简化模型，本文取为0；n为滤波器的阶数；N为滤波器数目；bi为滤波器的衰减因子，它将决定当前滤波器对脉冲响应的衰减速度，与中心频率的对应关系如下：

式中，bEBR(fi)为等效矩形带宽，与中心频率fi的关系如式（6）所示.GFCC 参数提取的步骤如图2所示.

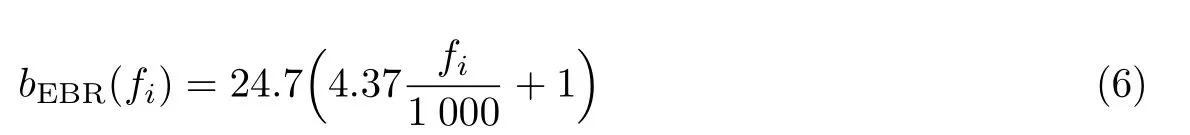
图2 GFCC 的提取过程Figure2 Extraction process for GFCC

GFCC 特征参数的提取过程与MFCC 基本相似，本文根据以往实验的经验值选用滤波阶数n=4,滤波器数目N=64，经过上面的提取过程得到特征参数Gn.同样地，为了显示语音的动态特性，本文对GFCC 的一阶差分∆GFCC 进行二次特征提取.∆GFCC 的计算方式同式（3），通过计算当前帧前后两帧变化得到特征参数∆Gn.

1.3 混合特征参数

Mel 滤波器是根据人耳听觉特征设计的，Gammatone 滤波器主要是根据基底膜上的频率感应而设计的.只要少量的几个参数就能拟合出抗干扰性强的特征参数，因此为了提高特征参数的抗噪性，本文将MFCC、MFCC 的一阶差分参数∆MFCC、GFCC 和GFCC 的一阶差分参数∆GFCC 作为混合特征参数，如式（7）所示：

式中，m和n分别为MFCC、GFCC 的特征参数阶数.

2 增减分量法对混合特征参数降维

由式（7）直接拼接起来的混合参数过于冗余，且GFCC 参数在大于30 维以后基本为0，对于识别而言并没有作用[9].此外，语音中的噪声主要体现在低维数的特征矩阵中，这些受影响的维数可能降低声纹识别率[10]，因此在实验中必须降低特征参数的维度，去掉受噪声影响大的维度.本文通过增减分量法评价特征参数的贡献度，根据贡献度的不同去除不必要的维数成分.增减分量法的平均贡献度函数如下：

式中，R(i)为贡献度，p(i,j)表示第i阶到第j阶作为语音特征参数应用于识别系统时的识别率.在实际应用增减分量法时，首先检测特征参数每个维数Ci ∼Cj组合的识别率，然后由式（8）计算每个维数Ci的贡献度.

3 高斯混合模型

GMM 是一种应用较广泛的说话人识别模型，具有运算速度快、训练复杂度低、鲁棒性好的优点.使用GMM 进行识别就是根据说话人的特征参数分布为每一个说话对象建立一个GMM 模型库，这个库可用来确定说话人的身份.M阶高斯混合模型的表达式如下：

式中，x表示1 个D维的随机向量；bi(x)为高斯概率密度函数，共有M个；pi为第i个分量的权重，通过多个高斯分量拟合成说话人的GMM 模型λ.在模型训练阶段，根据最大期望算法将模型进行多次迭代，计算每个说话人的GMM 模型.在识别阶段，对待识别语音进行特征提取，将特征矩阵与训练过的各个说话人模型一一进行匹配，计算特征矩阵属于每个说话人模型的概率，则最大概率的说话人即为最终识别结果.

4 实 验

仿真实验在MATLAB 2015b 上实现，实验用的语音库容量为100 人，其中男女各50 人，每人录制10 段6 s 的语音，其中7 段用来训练，剩下3 段进行识别.对语音的预处理设置如下：预加重系数为0.94，采样率为16 kHz；加窗类型为汉明窗，帧长为16 ms，帧移为8 ms.建立16 阶高斯混合模型进行说话人声纹识别，其最大迭代次数为100.

首先分别采用单一MFCC、∆MFCC、GFCC、∆GFCC 作为特征参数，通过不同维度的组合进行说话人识别实验，以验证各分量对识别结果的影响.MFCC、∆MFCC、GFCC、∆GFCC的实验结果分别如图3∼6 所示.图中右侧线段表示不同维数组合的起始分量，各数据点横坐标代表终止分量.在图3中，“×”线段第1 个数据点代表以MFCC 第1 维C1作为特征的识别率，第2 个数据点代表C1和C2作为特征的识别率.以此类推并由图3可知：将MFCC 参数C1和C15维组合作为特征参数达到了全局最高的识别率，之后随着维数的增加，识别率并未上升，而是稳定在80%左右.根据式（8）可以计算出MFCC 参数每个维度的贡献度如图7（a）所示，大于C16维的贡献度快速下降.∆MFCC 可以作为表征语音动态变化的特性，但作为单一特征参数进行识别的效果并不理想，于是可以根据实验计算出各维度对识别结果的影响.由图7（b）可知，MFCC 参数C1和C13的贡献度较高.同样由图4、图5、图8可知：GFCC 在大于21 维的贡献度下降迅速，∆GFCC 在大于23 维的贡献度较低.

图3 MFCC 的各维度组合识别率Figure3 Recognition rate of different combination of MFCC dimension

经过上述实验可知：到达一定维数之后，增加维数并不会提高识别率.为了精简参数不产生冗余又能保留说话人的声纹特征，本文选择MFCC 的前15 维、∆MFCC 的前13 维、GFCC 的前21 维、∆GFCC 的前23 维构成最终的特征参数，如式（10）所示：

对于组合后的特征参数，为验证它在不同噪声环境不同信噪比下的识别率，分别采用NoiseX-92 噪声库中的白噪声（white）、汽车噪声（volvo）、粉红噪声（pink）、工厂噪声（factory）进行说话人识别实验，并与无噪声情况下的识别率进行比较，所得实验结果如图9所示.可以看出：对于纯净的语音，以MFCC 为特征进行识别的识别率高于以GFCC 为特征进行识别的识别率.然而在低信噪比条件下，MFCC 的识别率大幅度下降，抗噪性能较差；而GFCC 的识别率下降比较缓慢，抗噪性能较好.本文综合两种倒谱参数的优点，提出将MFCC+∆MFCC+GFCC+∆GFCC 混合特征参数用于说话人识别.从图9的数据中可以看出：本文提出的混合倒谱特征参数识别方法在不同噪声环境下的识别率均明显高于其他特征提取方法，且受信噪比的影响程度也小于其他方法.

图4 ∆MFCC 的各维度组合识别率Figure4 Recognition rate of different combination of ∆MFCC dimension

图5 GFCC 的各维度组合识别率Figure5 Recognition rate of different combination of GFCC dimension

图6 ∆GFCC 的各维度组合识别率Figure6 Recognition rate of different combination of ∆GFCC dimension

图7 MFCC 及其差分参数各维度贡献度Figure7 Contribution of each dimension of MFCC and its differential parameter

图8 GFCC 及其差分参数各维度贡献度Figure8 Contribution of each dimension of GFCC and its differential parameter

图9 不同环境下的识别率Figure9 Recognition rate under different environments

5 结 语

本文针对常见的语音特征参数有效维数不足以及抗噪性能差等问题，根据各维度的贡献度大小将MFCC、∆MFCC、GFCC、∆GFCC 这4 种混合倒谱特征参数中贡献度较大的维度组合成新的混合特征参数；然后将混合倒谱特征参数送入16 阶高斯混合模型进行说话人识别.MATLAB 仿真实验表明：以不同噪声和不同信噪比情况下的识别率来衡量，本文所使用的混合倒谱特征参数方法相对于其他特征参数方法均有所提高，因此具有良好的抗噪性能.