用于磁敏免疫测量的激励磁场设计
刘 伟,张亚鹏,周凯波,赵兴一
(华中科技大学自动化学院,湖北武汉 470074)
0 引言
磁敏免疫测量中,如何实现可控的高均匀度、大均匀区间的激励磁场是整个测量系统的基石。目前,用于磁敏免疫测量系统的激励磁场主要有亥姆赫兹线圈、螺线管、电磁铁等方式。其中亥姆赫兹线圈通过对其尺寸进行合理的设计可以达到大的均匀区间[1],但是当需要产生较大的磁场强度的时候,就需要增加线圈的匝数和激励电流,如此则需要另外设计冷却系统来解决线圈的发热问题;螺线管方式只是在螺线管的中间部分产生均匀的磁场[2],螺线管封闭不利于测量的操作,并且也会存在线圈发热的问题。电磁铁的方式可以利用磁芯的高导磁特性,给较少匝数的激励线圈通以较小的电流来磁化磁芯,从而利用磁芯来产生所需要的磁场,如此可以解决发热的问题。
如果要利用电磁铁产生的磁场来作为系统的激励磁场,则需要给磁芯开以合适的气隙,利用气隙的磁场来激励样品,从而实现测量,但是气隙越大,磁场的均匀度越差,研究表明[3],当磁芯的直径与气隙大小的比值大于4时,在气隙中才能产生较好均匀度的磁场,但是由于测量样品容器的限制,测量的气隙不能太小。因此本文就如何设计大气隙激励磁场进行研究,并对气隙磁场的均匀性进行了相应的修正。
1 磁敏免疫测量装置结构
图1是基于本文所要设计的电磁铁结构来实现磁敏免疫测量系统的结构框图。信号源给励磁线圈一定的励磁电流来磁化磁芯,从而在气隙中产生所需要的激励磁场,样品在气隙磁场的激励下产生被测磁信号,通过磁传感器(TMR传感器)感应样品所产生的信号,再经过相应的信号调理和数据处理来分析样品中的物质的磁性。

图1 磁敏免疫测量装置结构
在上述系统中,样品容器使用标准的0.5 mL EP管,EP管的直径为8 mm,再加上磁传感器芯片的厚度,如果按照磁芯的直径与气隙大小的比值大于4来设计,磁芯的直径会显得过大而使得系统臃肿,而且磁芯越大,边缘效应会越严重,从而会增加系统的功耗,因此本文采用标准的R-30铁芯(2R=19.5 mm)。而根据样品容器和磁传感器的厚度设计气隙的大小为13 mm,在这种情况下并不能满足磁芯的直径与气隙大小的比值大于4,因此气隙的磁场会显得很不均匀,因此需要对气隙的磁场进行修正。
2 气隙磁场分布的理论计算
采用等效磁荷理论分析理论上被均匀磁化的磁极之间的磁场分布。由于磁体的磁化是沿一个方向并且是被均匀磁化的,因此磁体中的体磁荷密度恒为零[4],即
(1)

因此气隙中的磁场由磁体极面的面磁荷密度决定。磁体面磁荷密度的大小为
(2)
标量磁位与面磁荷密度有如下关系
(3)
由文献[5-6],气隙磁场强度可由式(4)得出:
(4)
式中:H+、H-分别是正磁荷和负磁荷产生的磁场强度;S+、S-分别为正磁荷和负磁荷所在的平面。
考虑R型铁芯(圆形极面)形状的气隙磁场分布计算,图2为圆形板面的气隙磁均分布计算图。

图2 气隙磁场分布计算图
考虑气隙中任意一点P(x,y,z)在y轴方向的磁场强度
(5)
式中ds=dηdε,并且η2+ε2≤R2。
同理可得
(6)
以场点位于y轴上为例分析,即P(0,y,0),在气隙中d>y,此时由Hy=Hy+-Hy-得:
(7)
式中:Br为磁极的磁化强度;μ为磁极的磁导率;R为磁极的半径;2d为气隙大小。
由式(7)可知,气隙中磁芯中轴线上的磁场与y值的大小有关,因此磁场是不均匀的。定义磁场的最大不均匀度为
(8)
提高磁场均匀度的方法有很多种,有在磁极加垫补线圈法[7]、精细的设计磁极的尺寸、在电磁铁磁芯边缘添加补偿环等方式,本文采用第三种方式来进行设计。
加补偿环的结构如图3所示,依据式(5)和式(6),被均匀磁化的补偿环在气隙中轴线上产生的磁场为

图3 带补偿环气隙磁场计算图
(9)
(10)
式中:Δd为补偿环的宽度;ΔR为补偿环的厚度。
根据磁场的叠加定理,带补偿环的磁芯在气隙中轴线上产生的磁场为
(10)
由磁场的最大不均匀度计算公式可知,气隙磁场的均匀度与磁极半径R、气隙大小2d、补偿环宽度Δd以及补偿环厚度ΔR相关。通过合理的设计补偿环的宽度和厚度可以提高磁场的均匀度。
3 电磁场仿真分析
根据前文的设计与理论计算,利用Ansoft软件对气隙磁场进行仿真分析。按照上述设计的尺寸,在Ansoft环境中按照1∶1建立有限元仿真模型,对3D模型进行有限元分析网格剖分。模型结构如图4所示。

图4 电磁铁有限元仿真模型
在该磁场产生装置中,磁芯的材料选取的是B30P105型取向硅钢片,硅钢片具有低铁损、高导磁率的特点。
励磁线圈采用0.5 mm直径的紫铜线材漆包线绕制而成,给2个激励线圈通以相同频率和匝数的励磁电流,在对补偿环的外径以及直径作相应的变化的时候计算相应条件下磁场的均匀度如图5所示。
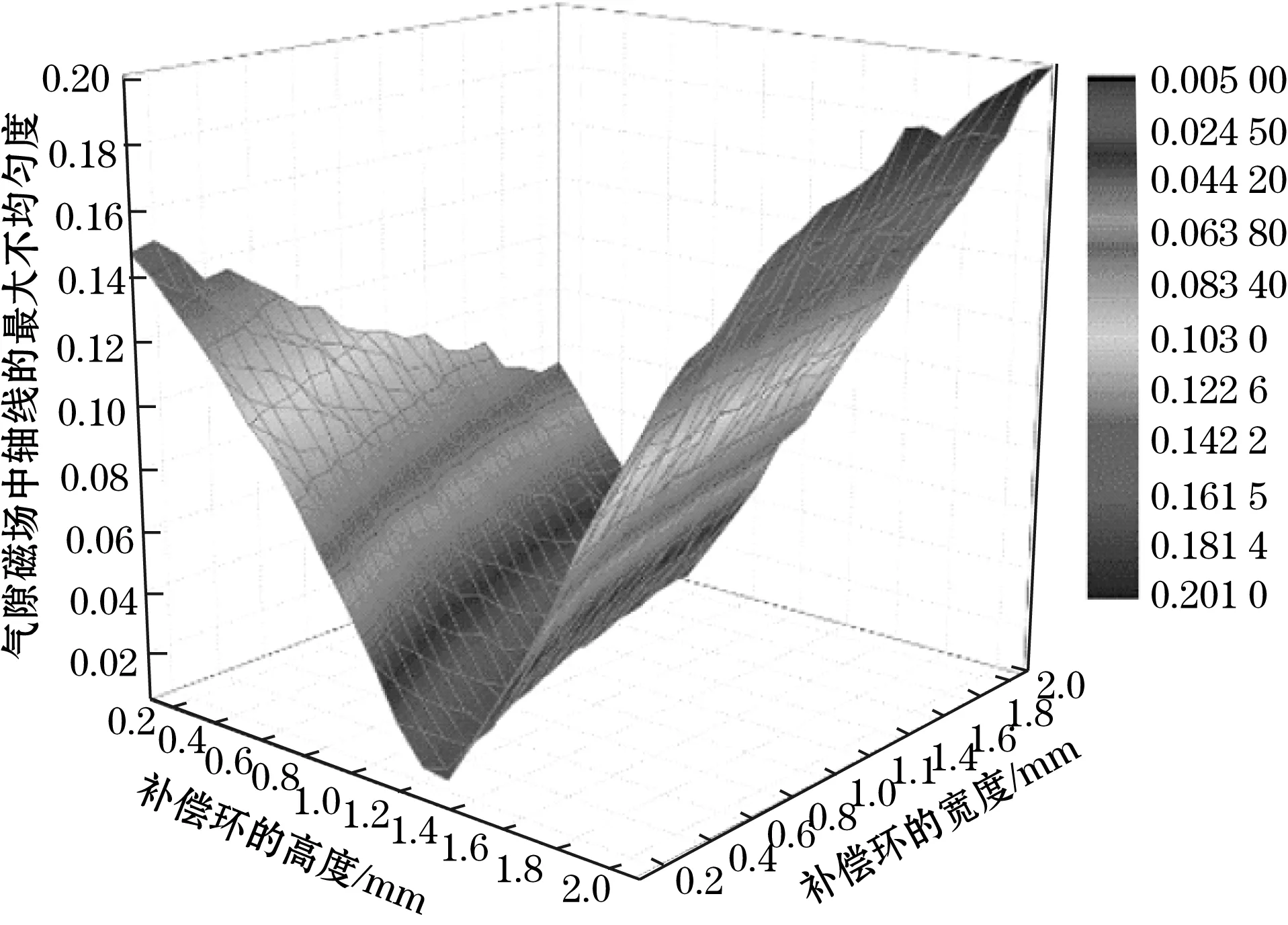
图5 气隙磁场的最大不均匀度和补偿环宽度以及高度的关系
由气隙磁场的理论计算依据仿真的数据可知补偿环的宽度Δd和厚度ΔR满足一定的条件的时候,气隙磁场的最大不均匀度达到最小。根据实验结果,取Δd=0.9 mm(图6)和ΔR=1.3 mm(图7)时相对应变量变化时磁场不均匀度进行对比。

图6 Δd=0.9 mm时ΔR与φ的关系

图7 ΔR=1.3 mm时Δd与φ的关系
从上面的仿真结果可知,当补偿环的宽度或者补偿环的厚度确定时,存在使气隙磁场最大不均匀度最小的相应的补偿环厚度和补偿环宽度。这与之前的理论计算相符合。
图8对补偿环和未加补偿环情况下气隙磁场分布进行对比。

图8 加补偿环前后磁场分布对比

图9 未增加补偿环气隙的磁场分布
图9和图10分别表示未增加补偿和增加了补偿环之后气隙磁场分布的仿真图,根据仿真图结果可知,在其他条件相同的情况下,当给磁芯增加内径为6.5 mm,外径为7.8 mm,长度为0.9 mm的补偿环之后,气隙磁芯轴线上磁场的的最大不均匀度从13.84%降

图10 增加了补偿环之后气隙的磁场分布
低到0.553%,不均匀度提高了2个数量级。同时,从上图中还可以看出,磁芯气隙径向的磁场也的均匀性也得到了很大的改进。
4 结论
当磁芯的直径与气隙的大小的比值小于4时,大气隙C型磁铁气隙磁场具有很大的不均匀性,本文从大气隙C型磁铁的设计出发,对气隙的磁场进行了理论计算,并使用补偿环的方式对气隙的磁场进行了修正,计算和仿真结果表明,补偿环的厚度ΔR=1.3 mm和宽度Δd=0.9 mm时会使得气隙的磁场均匀度得到最大的修正,气隙的最大不均匀度从13.84%降低到0.553% 。

