摆动式电磁能量收集装置的设计与仿真
张 端,陈挺任,王满州
(1.浙江工业大学计算机科学与技术、软件学院,浙江杭州 310023;2.浙江工业大学信息工程学院,浙江杭州 310023)
0 引言
随着微电子技术、微机电系统技术和微流控技术的革新,一大批具有体积小,寿命长,功耗低等特点的传感器被广泛应用于无线传感网络以及物联网中,实现环境监测、结构健康监测、植入式医疗检测、汽车胎压监测等社会生活中多方面的功能需求[1]。然而,能源供应成为制约传感器节点推广应用的主要瓶颈之一。目前无线传感器节点中最为常见的供电方式还是使用化学电池,但是电池有寿命较短、对环境有一定污染、需要定期更换等缺点和不便。一个可行的替代方案是采用自给能源,也就是利用能量收集技术在传感器节点所处的环境捕获能量。自然界中存在不同频率和强度的振动,众多学者纷纷考虑振动能量收集技术,将环境中的振动能转换成电能为传感器节点供电[2-8]。2014年,BERDY D F等人利用磁悬浮技术设计的电磁式振动能量收集装置在2 Hz的工作频率下,实验测得的平均功率为342 mW[9]。2015年,浙江工业大学的张端副教授等人设计了一款低频振动能量收集装置,该装置在1 Hz的振动频率下产生的感应电动势可达1.5 V,最大有效功率为12.02 mW[10]。2016年,美国的PEDCHENKO A V等人设计了一款电磁振动能量收集装置,在最佳频率为8 Hz的振动下,能够获取75 mW的功率[11]。
文章设计的一款摆动式电磁低频振动能量收集装置具有以下特点:
(1)形成了闭合磁路,摆动过程中闭合磁路交替通断从而产生线圈电动势,漏磁少;
(2)摆动式结构易于起振和维持振动;
(3)通过摆动磁轭与外部磁轭上齿的合理布置,从原理上消除了电磁装置中容易出现的切向磁力(即定位力),消除了装置摆动的主要阻力;
(4)装置还采用了多齿结构,提高铁芯中磁通量的变化频率。
1 结构模型和工作原理
1.1 摆动式电磁能量收集装置的结构
摆动式电磁振动能量收集装置的结构模型如图1所示。该结构包括具有对称磁齿的外部上磁轭、外部下磁轭、放置线圈的铁芯、永磁体支架、永磁体、摆动上磁轭、摆动下磁轭和漆包线线圈。外部上磁轭和下磁轭均由软磁材料制成,它们固定于装置的外壳(图中未表示)。永磁体为圆柱体,借助上下支架与外部上、下磁轭形成整体,永磁体上部为N极,下部为S极。上、下支架均为软磁材料零件。永磁体采用磁能积、矫顽力和剩磁比较高的稀土材料NdFeB。摆动上磁轭和下磁轭内均有半圆孔,而半圆孔的另一侧则加厚,以保证外界振动下摆动磁轭可获得较大的转矩。摆动上磁轭和下磁轭通过铁芯相连形成一个固联的整体,它们均由软磁材料制成,铁芯上缠绕漆包铜线圈。摆动上磁轭和下磁轭通过轴与外壳相接,能相对外壳转动,外壳由非导磁材料制成。为了满足装置既能够产生有效电压,又能够满足小巧的要求,摆动式电磁振动能量收集装置尺寸参数设计如下:永磁体设定外径为6 mm,高度为18 mm的圆柱体;外部磁轭厚度为5 mm,外径为100 mm,齿顶直径为80 mm;摆动磁轭厚度为5 mm,齿底直径为70 mm,齿顶直径为79.8 mm ,同时摆动磁轭内部切割一个半径为30 mm的半圆孔;铁芯直径为6 mm,高度为20 mm。

图1 摆动式电磁振动能量收集装置去除外壳图
外部上磁轭和下磁轭具有均匀布置在内部的12个齿,齿顶与齿底宽度相同,均为15°转角。摆动上磁轭、摆动下磁轭同样具有均匀布置的8个齿,齿顶与齿底的转角角度比为4∶11,其中齿顶转角为12°,齿底转角为33°。该结构保证了摆动磁轭上的齿顶与外部磁轭的齿顶正对时,摆动磁轭上其相邻的齿顶就会和外部磁轭的某齿底正对。此时会有4个摆动磁轭磁齿与外部磁轭磁齿相连,而另外4个摆动磁轭的磁齿与外部磁轭磁齿间隙相对。
1.2 能量收集装置的工作原理
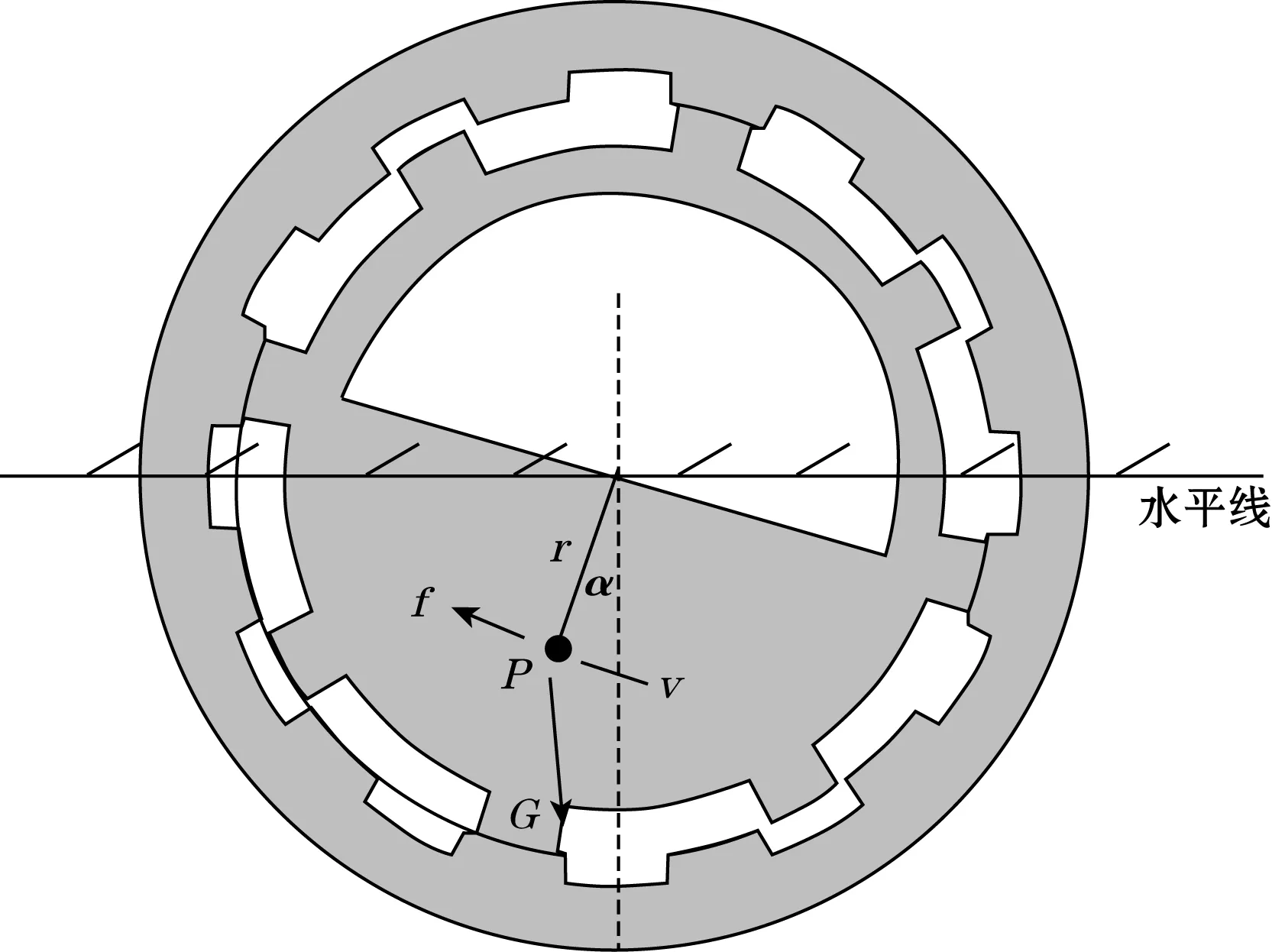
图2 摆动磁轭受力分析图
根据能量守恒定律公式可得:
(1)
式中:W1为摆动过程产生的电能,W;W2为摩擦力所做的功,W;m为摆动磁轭的质量,kg;v1为初始速度,m/s;v2为摆动过程中的速度,m/s;β为装置摆放时与水平面的夹角,rad;G为摆动磁轭所受重力,N;r为质心P到转轴之间的距离,m。
f=f1+f2
(2)
式中:f1为摆动磁轭受到的磁力,N;f2为摆动磁轭受到的摩擦力,N。
由于装置设计的巧妙性,大幅减少了摆动磁轭摆动过程中受到的摩擦力,因此摩擦力做功忽略不计。根据式(1)和式(3)可得

(3)
从式(3)可以看出,电能W1与摆动角度、质心到转轴距离、摆动磁轭质量、摆动过程中受到磁力大小等都有关。
随着摆动磁轭绕转轴摆振,摆动上、下磁轭的齿顶与外部上、下磁轭的齿顶间气隙宽度发生变化,穿过线圈的磁通量也随之发生变化,从而在线圈中产生感应电动势。根据电磁感应定律:线圈中产生的感应电动势可以表示为
(4)
式中:Ecoil为线圈中的感应电动势,V;N为线圈匝数;Ψ为磁链,即穿过N匝线圈的磁通量之和,Wb;φ为穿过单匝线圈的磁通量。
图3给出了5个摆动的位置,从位置1到位置5是摆动磁轭瞬时针摆动30°的5个中间位置。为便于分析,把位置1中摆动上磁轭上齿顶与外部上磁轭齿顶正对的4个齿暂定为第一组,而摆动磁轭的另外4个齿定为第二组;同样可以确定摆动下磁轭上的第一组齿和第二组齿,在位置2到位置5过程中均采用此分组方法。下面分析摆动至位置1~5时,线圈磁通的变化:
位置1:摆动上磁轭的第一组4个齿顶与外部上磁轭齿顶正对。磁力线由永磁体N极发出,经过永磁体上支架、外部上磁轭、气隙、摆动上磁轭第一组齿、铁芯、摆动下磁轭第一组齿、气隙、外部下磁轭、永磁体下支架,回到永磁体S极。该位置下,与第一组齿相连的线圈中磁感应强度为最大,磁通量为最大值,与第二组齿相连的线圈中磁感应强度和磁通量为最小。此外,也会有占总磁通很小一部分的漏磁,通过外部上磁轭、摆动上磁轭第二组齿、铁芯、外部下磁轭第二组齿,永磁体下支架,回流永磁体;或者通过摆动上磁轭第一组齿、铁芯、摆动下磁轭第二组齿,外部下磁轭,永磁体下支架,再回流永磁体。
位置2:摆动磁轭顺时针摆动,其第一组齿顶与外部磁轭齿顶对应面积逐渐减小,而第二组齿顶与外部磁轭齿顶对应面积逐渐增大。磁感应强度在第一组齿上损耗加大,在第二组齿上损耗减小。磁力线从永磁体N极出发,经永磁体上支架、外部上磁轭所有齿、摆动上磁轭、铁芯、摆动下磁轭、外部下磁轭、永磁体下支架回到永磁体S极。此时,摆动磁轭第一组齿对应的线圈中磁感应强度和磁通量随摆动转动逐渐减小,而第二组齿对应的线圈中磁感应强度和磁通量随摆动转动逐渐增大。
位置3:摆动磁轭顺时针继续运动,其第一组齿与外部磁轭的齿相互错位,正对面积归零,同时第二组齿与外部磁轭的齿对应面积达到最大。磁力线从永磁体N极发出,经过永磁体上支架、外部上磁轭、外部上磁轭磁齿、摆动上磁轭第二组齿、铁芯、摆动下磁轭第二组齿、外部下磁轭、永磁体下支架到永磁体S极,与位置1的情形互为反向。此时,与第一组齿相关的线圈中磁感应强度和磁通量为最小值,仅有少量漏磁通过;与第二组齿对应的线圈中磁感应强度和磁通量为最大值。
位置4:继续顺时针摆动,摆动磁轭的第一组齿顶与外部磁轭齿顶对应面积逐渐增大,第二组齿顶与外部磁轭齿顶对应面积逐渐减小。此时磁力线与位置2的情况类似,磁力线会同时穿过摆动磁轭上所有的齿,穿过线圈的磁通方向相同,而磁通增量方向相反,线圈产生的感应电动势方向也相反。
位置5:从位置1以来,摆动磁轭顺时针转角达到30°。第一组齿对应的线圈中磁感应强度和磁通量回到最大值,第二组齿对应的线圈磁感应强度和磁通量回到最小值,磁通量完成一个周期变化。

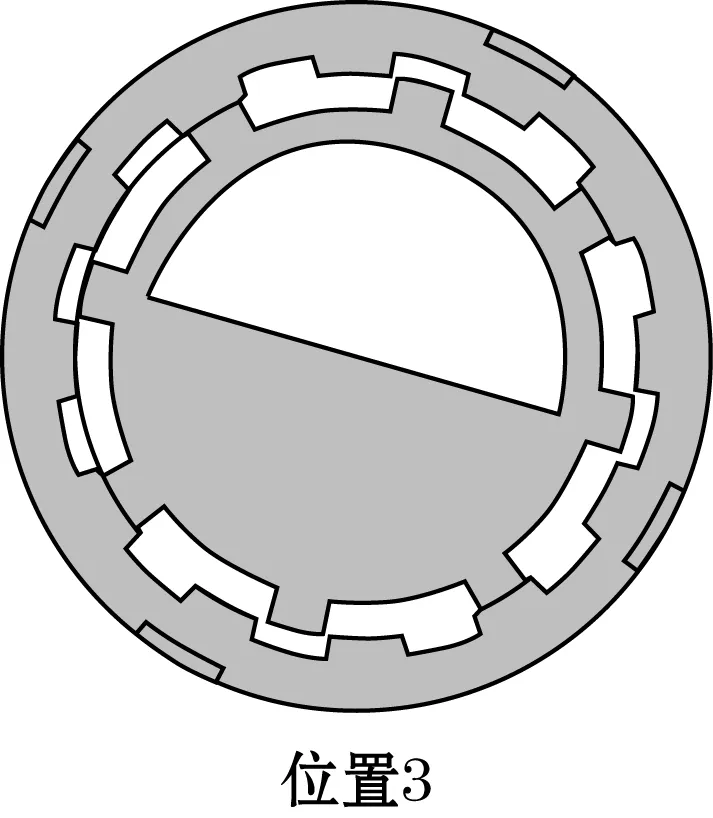
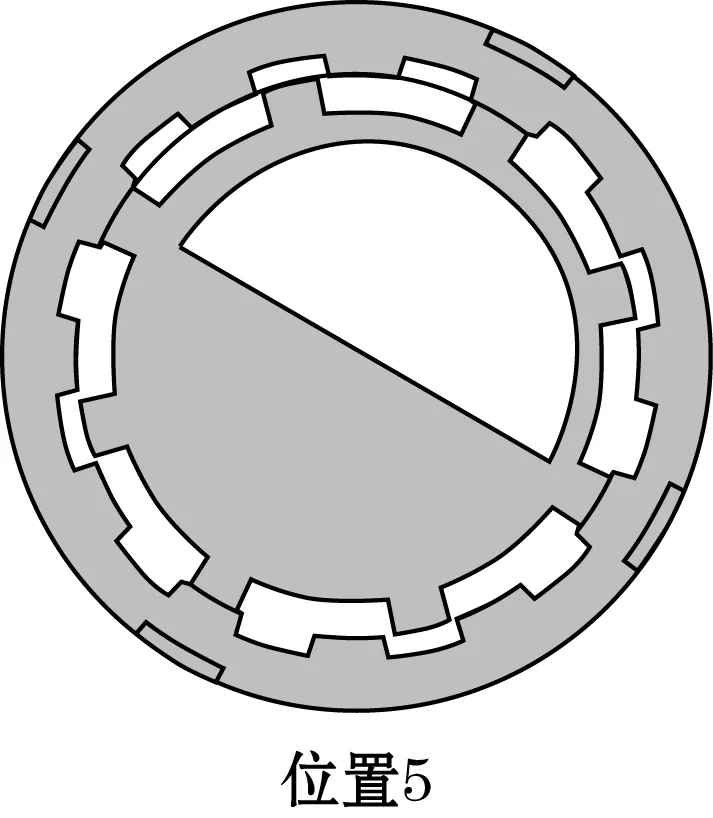
图3 装置摆动30°过程中的5个位置
2 参数设定与优化
2.1 参数设定
为获得最优装置参数,使用Ansoft Maxwell有限元分析软件对装置进行求解,通过静态仿真对装置的主要结构参数进行优化,并利用动态仿真分析模型工作效率。
首先使用Ansoft Maxwell根据上文给出的结构参数建立模型,之后进行材料设定。设定永磁体选择剩磁密度为1.3 T,矫顽力为450 KA/m的NdFeB稀土材料。导磁材料的选择为软磁材料硅钢。
完成整个模型的材料设定之后,需要对装置模型进行网格划分。网格划分是将结构模型进行有限元分解,便于Ansoft Maxwell软件进行求解。网格划分的尺寸会影响装置模型仿真结果的精确度,尺寸越小精确度越高,同时运算的时间也就越长,仿真中选择0.1 mm的网格划分尺寸。
求解是根据需求设定不同的求解项,文章根据漏磁和磁饱和等问题对装置结构参数进行仿真,并根据结果对装置进行优化。
2.2 参数优化
虽然设计了闭合磁路,少量漏磁仍难以避免;同时,软磁材料的选择,结构尺寸的变化,都会影响线圈中的磁感应强度,从而影响装置的发电效率。文章运用Ansoft Maxwell软件对装置做静态仿真,从气隙宽度、相对磁导率和摆动齿厚度3个角度定量分析了参数变化对线圈中磁感应强度和边缘效应的影响。
图4(a)表示了摆动磁轭与外部磁轭处于图2位置1时,气隙宽度变化对铁芯中磁感应强度的影响。空气的相对磁导率较低,气隙较大时,磁路中的磁力线会向外扩散,引起边缘效应。静态仿真设置气隙宽度从0.1~1 mm逐渐增大。从图中可以看到,气隙宽度为0.1 mm时,磁感应强度为最大。随气隙宽度变大,铁芯中的磁感应强度单调减小;气隙宽度越大,磁损耗越严重。但气隙宽度过小,加工难度将急剧上升。因此,气隙宽度定为0.15 mm。
选择软磁材料考虑的主要因素是相对磁导率,相对磁导率较小时,导磁性能太差,相对磁导率较高时,软磁材料加工工序繁复,价格昂贵,增加装置成本。图4(b)是相对磁导率与铁芯中磁感应强度之间的关系图。随着相对磁导率增大,铁芯中磁感应强度不断变大。当相对磁导率大于6 000时,曲线趋于平滑,磁感应强度增长缓慢。同时考虑到成本因素,文章装置选择相对磁导率为6 000的硅钢。
图4(c)是摆动磁轭厚度与铁芯中磁感应强度之间的关系图。调整厚度,摆动磁轭齿顶或者外部磁轭齿顶面积(二者相等)随之增大,铁芯中磁感应强度呈上升趋势,说明选择适当的摆动磁轭厚度,可以有效改善边缘效应和减小整个装置运行过程中的漏磁。但在该厚度达到4.5 mm之后,上升趋势变缓,本装置的摆动磁轭和外部磁轭的齿厚度均选择5 mm。
2.3 定位力与转矩分析
装置摆动过程中,静止的外部磁轭与运动的摆动磁轭间会有磁力,该磁力通常会形成运动的阻力,使运动件静止下来,停留在磁力最大的位置上,有外界干扰使运动件离开该位置后,也会被磁力拉回,稳定在原位置,这就是所谓定位力,这在电机中极常见的,因此电机需要较大的外部能量驱动。但对低频的振动能量收集装置,环境振动的驱动力本身较小,定位力会使装置无法工作,这是振动能量收集装置在设计上与电机明显的不同之处。
分析本装置的受力。由于摆动磁轭、外部磁轭的齿分布的对称性,摆动磁轭径向所受外部磁轭的磁力理论上合力为0。以图3位置1为例,考虑在外界振动下摆动磁轭略顺时针方向偏离图中位置时的切向磁力。此时,按上节区分的摆动磁轭第一组齿受其正对的外部磁轭上齿的逆时针方向磁力;而第二组齿受其相邻两个外部磁轭上齿的方向相反磁力,但两磁力的合力为顺时针方向的磁力,由第一、第二组齿后磁路的对称性可知,第二组齿所受顺时针与第一组齿逆时针磁力大小相等,可以平衡,因此理论分析出位置3的定位力为0。

(a)铁芯中磁感应强度和气隙宽度之间关系

(b)铁芯中磁感应强度和相对磁导率之间关系

(c)铁芯中磁感应强度和转子导磁磁轭厚度之间关系图4 静态仿真结果
进一步,通过静态仿真验证图3的位置2处,磁导率在1 000~9 000变化时,摆动磁轭切向和径向的受力情况。由图5可知,摆动在2个方向上的受力均mN数量级,摆动在不同相对磁导率情况下受力会有变化,其中切向最大磁力为34 mN,径向最大磁力为50 mN 。也就是摆动所受切向定位力为34 mN。而装置中摆动采用的材料为硅钢,根据摆动的体积和硅钢密度计算得出摆动的总重量为34.2 N,远大于摆动收到的定位力34 mN 。由此可以得知,装置的定位力可忽略不计。

(a)摆动磁轭切线方向受力和相对磁导率之间的关系

(b)摆动磁轭径向受力和相对磁导率之间的关系图5 摆动磁轭切线和径向方向上的受力
根据上面参数优化的结果,确定Maxwell动态仿真的参数:气隙宽度为0.15 mm,相对磁导率为6 000,磁轭厚度为5 mm,单个铁芯上所绕漆包线圈为1 000匝,导线直径为0.3 mm,直流电阻率 为241.8 Ω/km,线圈内径为3 mm,外径为5 mm。Maxwell的运动设置为从图2的位置1摆动,摆动周期为1 s,摆角为30°。
仿真得出摆动磁轭摆动过程中所受转矩与时间关系如图6所示,从图6可以看出,摆动时所受转矩在-49.2~25.8 mN·m之间变化。摆动重心位距离转轴30 mm处,计算得出装置实际所受到的最大定位力为1.667 N,远小于摆动磁轭自身所受重力34.2 N,因此摆动基本不受定位力的影响。

图6 摆动转矩分析
3 仿真结果
参数优化后的装置,其线圈中的感应电动势和线圈磁链的仿真结果如图7所示,优化后的单个线圈感应电动势幅值约为0.28 V,8个线圈总电压值为2.24 V 。优化后的装置能量收集效率为优化前的3.5倍。图8为优化后的装置的磁感应强度分布图。
综上,根据公式:
R=Nρπ(di+d0)/2
(5)
式中:R为一匝线圈总电阻,Ω;N为线圈匝数;ρ为直流电阻率,Ω/m;π为圆周率;di为线圈内径,m;d0为线圈外径,m。
计算出单个线圈上的电阻为24.3 Ω。根据公式:
(6)

(a)感应电动势与时间的关系曲线
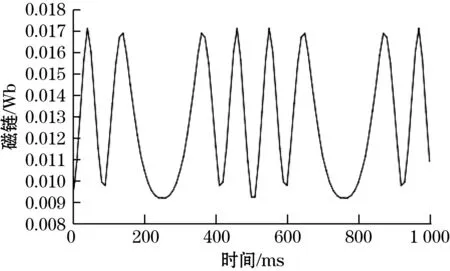
(b)线圈中磁链与时间的关系曲线图7 优化后结构的动态仿真结果


位置1

位置2

位置3
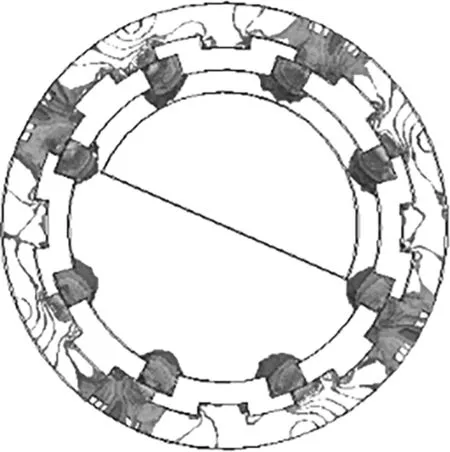
位置4
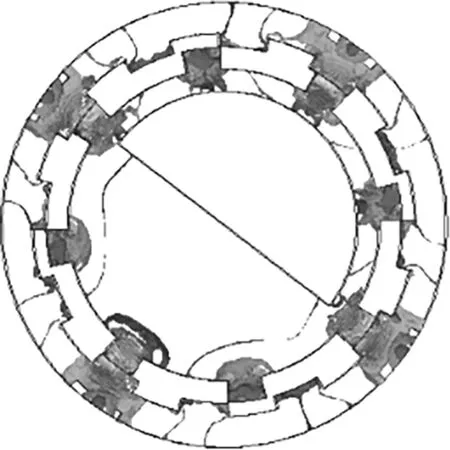
位置5
式中:P为装置最大发电功率;Ucoil为8个线圈产生的总电动势;R为一匝线圈的内阻。
当负载电阻等于线圈内阻时负载有效功率可达最大。计算得出负载最大有效功率为103.2 mW。对比2017年1月刊登的文献[12],设计了一种结构精巧的电磁振动能量收集装置,在6 Hz频率的手动摇摆下能够产生2.92 mW的功率。文章装置与之相比,虽然体积和线圈数略微大一些,但是发电功率提升很大。因此文章装置优势明显。
4 结论
文章提出一种摆动式电磁振动能量收集装置,设计了外圈12齿内圈8齿结构,最大化平衡了装置摆动时受到的电磁定位力。同时,装置的摆动重心偏移原点的设置,能够充分感应装置本身加速度的变化以及所在平面的变化,有效地收集能量。利用Ansoft Maxwell动态仿真,该装置在摆动频率为1 Hz的情况下,产生的总感应电动势可达2.24 V,最大有效功率为103.2 mW,可为多数的无线传感网络节点供电,具有一定应用前景。

