金属-光折变材料复合全息结构对表面等离激元的波前调控*
谌璐 陈跃刚
(贵州大学物理学院,贵阳 550025)
(2018 年9 月6 日收到; 2018 年12 月27 日收到修改稿)
表面等离激元(surface plasmon polaritons,SPPs)控制具有重要意义. 表面电磁波全息法是在金属表面设计能有效控制SPP 传输的凹槽阵列结构. 本文提出一种新的SPP 传输的控制方法,利用金属-光折变材料复合全息结构控制SPP 传播. 在金属表面覆盖一层光折变材料,两束SPP 波在光折变材料内干涉生成全息结构,利用此全息结构能够控制SPP 的传播. 通过时域有限差分法模拟验证,结果显示,通过金属-光折变材料复合全息结构可以有效地控制SPP 波束的传输,实现SPP 平面波束的单点聚焦、两点聚焦,以及生成零阶和一阶高斯SPP 波束. 经过优化发现,光折变材料的最佳厚度为 3 .3 μm ,最佳折射率调制度为0.06. 现有SPP 控制器件主要是通过离子束刻蚀,而金属-光折变材料复合全息结构不需要刻蚀,从而扩展了SPP 控制的器件的制作方法,为SPPs 的全光控制提供了新的思路,使SPP 全光控制成为可能,进一步实现了SPP 全光开关等功能.
1 引 言
表面等离激元(surface plasmon polaritons,SPPs)是金属表面电子集体振荡形成的一种波,并局限于金属与介质之间的界面传播[1,2]. 1902 年,Wood[1]在实验中首次发现了SPPs. 1998 年,Ebbesen等[2]发现SPPs 共振导致亚波长增强透射现象. 之后,SPPs 引起了研究者浓厚的兴趣. 由于光强增强和突破衍射极限两个独特的性质,SPPs 具有广泛的应用前景,比如SPP 传感器[3,4]、集成光学[5]、亚波长分子手术[6]和SPP 激光器[7,8]等. 很多器件被提出来控制SPPs,以实现SPP 波束在预设的路径中传播,如波导器件[9,10]、波分复用中的解复用器件[11]、路由器件[5]等,还有阵列结构操控SPPs散射,如牛眼结构[12]、亚波长小孔阵列结构[13]、全息凹槽结构[14]等.
现已设计了很多SPPs 波束的控制元件. Li等[15−17]利用渐变周期纳米结构调制面内的SPP波束散射,得到艾里SPPs 波束、汇聚SPPs 波束等,实现了波面控制. 在波长控制方面,Tanemura等[18]利用模拟退火算法设计了特定分布模式的纳米结构耦合自由空间中光波到SPPs 波束,使不同波长SPPs 波聚焦于不同位置. 还有Wang 等[19]也利用模拟退火算法设计波导阵列实现了SPPs多波长的聚焦和解复用功能. 另外,利用SPP 晶体可以实现二维的波长解复用器和多端口输出功能[20].Smith 课题组[21,22]利用液晶材料的取向光折变效应,在金属表面产生了简单的光栅结构,控制SPP.
表面电磁波全息法(surface wave holography,SWH)是一种SPP 功能器件的设计方法. 利用其在金属表面设计凹槽阵列结构可有效控制SPPs的传播,主要实现三方面的控制. 第一,控制金属表面的SPPs 向自由空间散射,实现散射波在自由空间的单点聚焦、两点聚焦、波面整形[23−25]. 第二,控制金属表面内SPP 波束的传播,如SPPs 波束侧向聚焦[26,27]、复杂波面控制[28]、横纵模可控的SPPs 共振腔[29]等. 第三,自由空间光束耦合到SPPs 的控制[30]. 表面SWH 设计的过程简单,结构直观,设计器件功能多,具有很广的应用前景.
以上这些方法设计的结构只可用聚焦粒子束或聚焦电子束等实验方法直接在金属表面刻蚀而得到[15−30],制作方法受到了限制,而且这些结构都是直接刻蚀在金属表面上,从而是固定不变的,不能实现实时灵活的操控. 而光折变材料器件不需要刻蚀,且能够实时灵活操控,并已经有了大量关于光折变材料的研究. 当光照射进入光折变材料,如铌酸锂、砷化镓[31]等时,激发材料中自由电荷,自由电荷漂移到暗光区,形成空间电荷分布,产生了空间电场,最终空间电场通过线性电光效应改变材料折射率. 除了常见的光折变材料,也有其他材料能够将光强分布转化为折射率分布,如液晶盒[22]、光致变色材料[32]等. 光折变材料应用十分广泛,如应用于光信息处理、光信息储存、光图像转换等方面. 光折变材料还可以制作全息图,将光强信息转化为折射率分布,记录下来.
本文提出用金属-光折变材料复合全息结构控制SPPs 波束的传播. 在金属表面覆盖一层光折变材料,通过SPP 波束的干涉在光折变材料中产生全息结构,利用此全息结构实现SPP 波传输的灵活控制.
2 金属-光折变材料复合全息原理
考虑控制SPPs 波束在金属和电介质之间的界面上传播,提出了金属-光折变材料复合全息原理,包括写入和读出过程. 在写入过程中,在金属与介质的界面上,SPP 物波与SPP 参考波干涉,得到强度分布(图1(a)). 设金属表面的介质为光折变材料,则光强分布可以转化为相应的折射率分布型全息图,此全息图能够控制金属表面光强相对较弱的SPPs 的传播. 在读出的过程中(图1(b)),与原来的参考SPP 波束共轭的波束作为再现波,入射到全息图结构区域. 经过全息图结构对再现波束的反射和散射,物波的共轭波被重构出来.
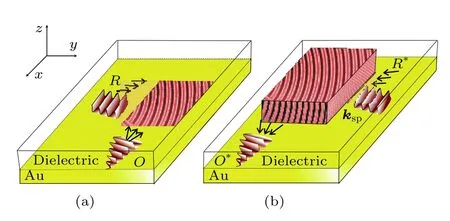
图1 金属-光折变材料复合全息原理示意图 (a)写入过程; (b)读出过程Fig. 1. Schematic of metal-photorefractive material complex holography: (a) Writing process; (b) reading process.
在写入过程中,设参考SPP 波RW(x,y)=R(x,y)exp[−i·krSP·r(x,y)] ,物SPP 波OW(x,y)=O(x,y)exp[−i·koSP·r(x,y)]. 物波和参考波干涉,光强分布为

其中K(x,y)=krSP−koSP为介质光栅矢量. 通过光折变材料将光强信息转化为折射率分布,
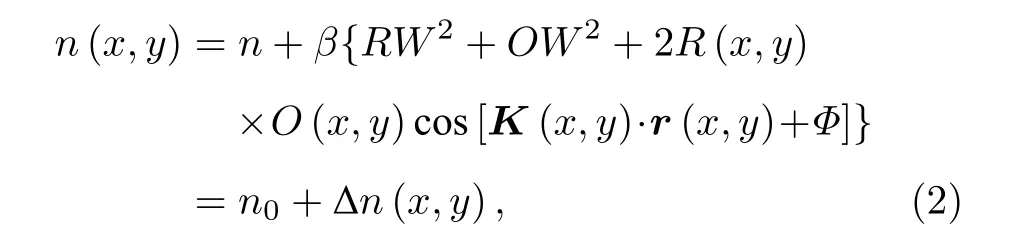
其中,β为光折变材料感应系数,Δn(x,y) 为折射率调制函数,Φ为空间电荷场相对于记录光强的干涉分布产生的相移. 没有外加电场时,Φ=π/2 . 此相移是全息光栅整体的相移,相当于结构整体移动了1/4 个条纹距离,对再现是没有影响的. 此光折变材料全息图位于金属表面,形成金属-光折变材料复合全息图,包含物波OW(x,y) 的信息.
金属-光折变材料全息图可以看成是三维全息图在传输方向的一个切面. 能利用体全息理论分析金属-光折变材料复合全息图,讨论影响全息图再现效率的因素. 在读出过程中,当再现波的入射角偏离写入过程的参考波角度为 Δθ时,相位失配因子δ可表示为[33]
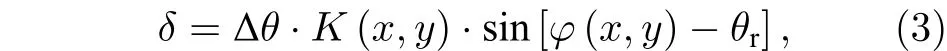
其中φ(x,y) 为折射率光栅的矢量倾角. 衍射波相位失配因子由折射率光栅的空间变化而产生,全息图的衍射效率与相位失配因子有关,

式中,体全息的耦合强度ν和布拉格失配参量ξ分别为

其中d为全息图在再现波传播方向上的尺度,θr和θs分别为参考波和物波的方位角. 当再现波的入射角偏离参考波的角度 Δθ=0 时,即再现波满足布拉格条件时,衍射效率为
纪民尚,到现在还有好多山东球迷认为他的名字应该是“纪民尚”,或者简称为没有争议的“大纪”更妥当。多年的媳妇熬成婆,大纪在尝试了女篮主教练、男篮主教练、俱乐部副总、省篮管中心副主任等多个职位之后,这个赛季第一次作为俱乐部总经理的身份来驾驭一支球队,对不起,应该是两支球队——山东西王男篮和女篮。

由(7)式可知,在满足布拉格角入射条件时,衍射效率将随 Δnd增加而振荡变化. 因此,控制光折变材料的折射率调制度和尺度,可使衍射效率达到最佳状态. 通过研究,我们找出了光折变材料全息图在衍射效率最大时对应的折射率调制度和全息结构尺度最佳值.
3 模拟结果
设计金属-光折变材料复合全息结构控制SPP 波的传输. 设计全息图将平面的SPP 波分别侧向精确聚焦到1 个点和2 个点,以及生成0 阶和1 阶高斯SPP 波束. 设z=0 的xy平面为金属与介质的界面,在此界面,SPP 波传播的波矢量ksp=neffk0,其中和εd分别是金属和介质的介电常数. 考虑控制自由空间中波长为λ0=1.064 μm 的光波,金属在此波长段介电系数取εm=−48.75+3.64i . 设介质的折射率的常数为n0=1.45 . 在模拟设计中,考虑到光折变材料的折射率调制度n1值比较小(n1≪n0),设计全息图过程中计算物波和参考SPP 波束的波矢ksp大小时,光折变材料的介电系数取εd=n02. 这样能够大大简化设计过程. 还有在设计中将干涉光强I(x,y) 用最大值进行归一化得到(x,y) ,然后乘上系数 Δn,得到折射率调制函数 Δ(x,y) ,这与(2)式中 Δn(x,y)折射率调制函数对应. 这里 Δn称为折射率调制度,在全息图再现中非常重要.
首先,设计全息图结构将沿y方向传输的SPP 平面波侧向汇聚到1 个点O(8 μm,0) 处. 在写入过程中,参考波设为沿y方向传输的SPP 平面波,表达式为RW=exp(−i·ksp·y) . 将此平面波汇聚到金属表面上点O(8 μm,0) 处,则物波设置为由O点发出的柱面,表达式为

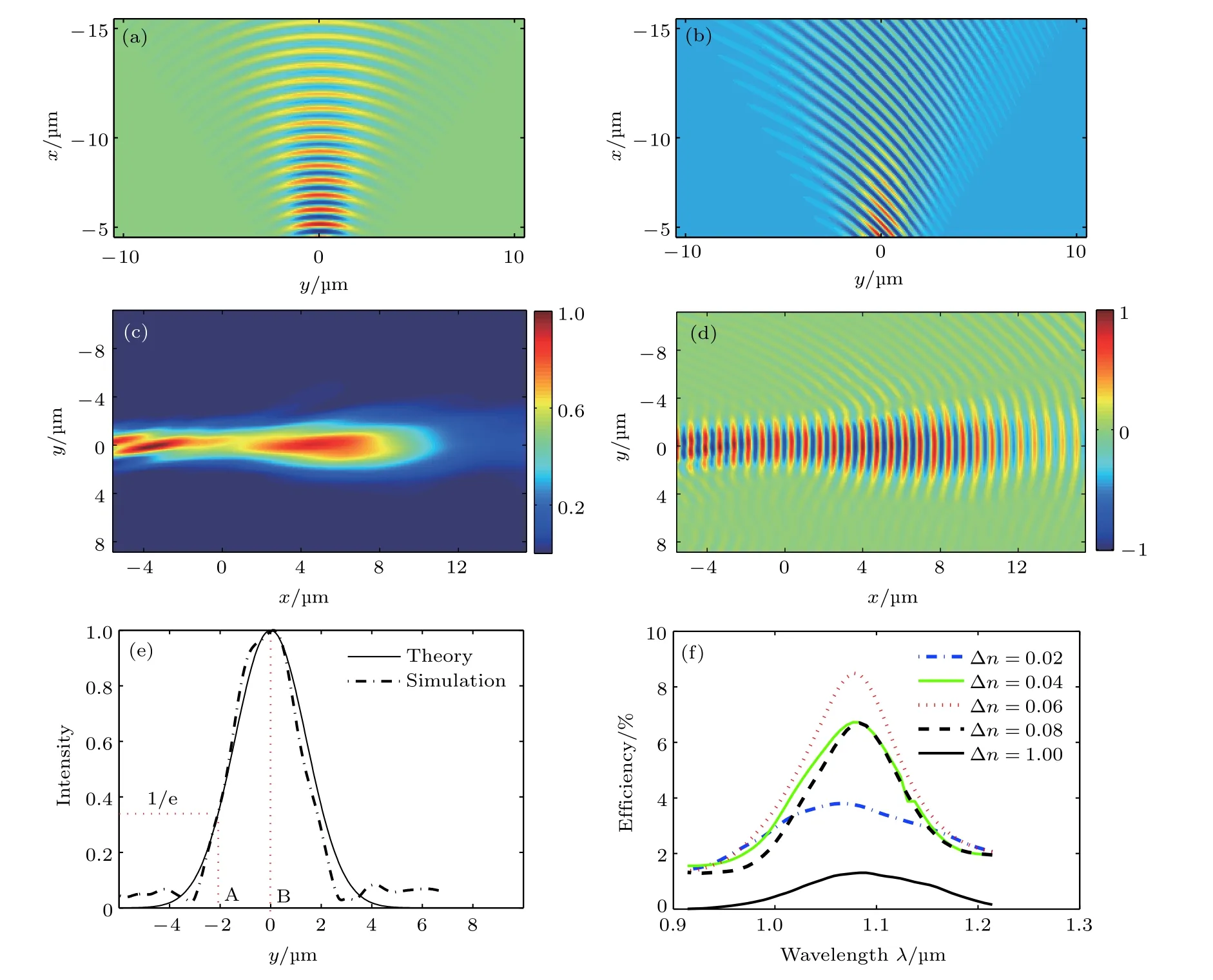
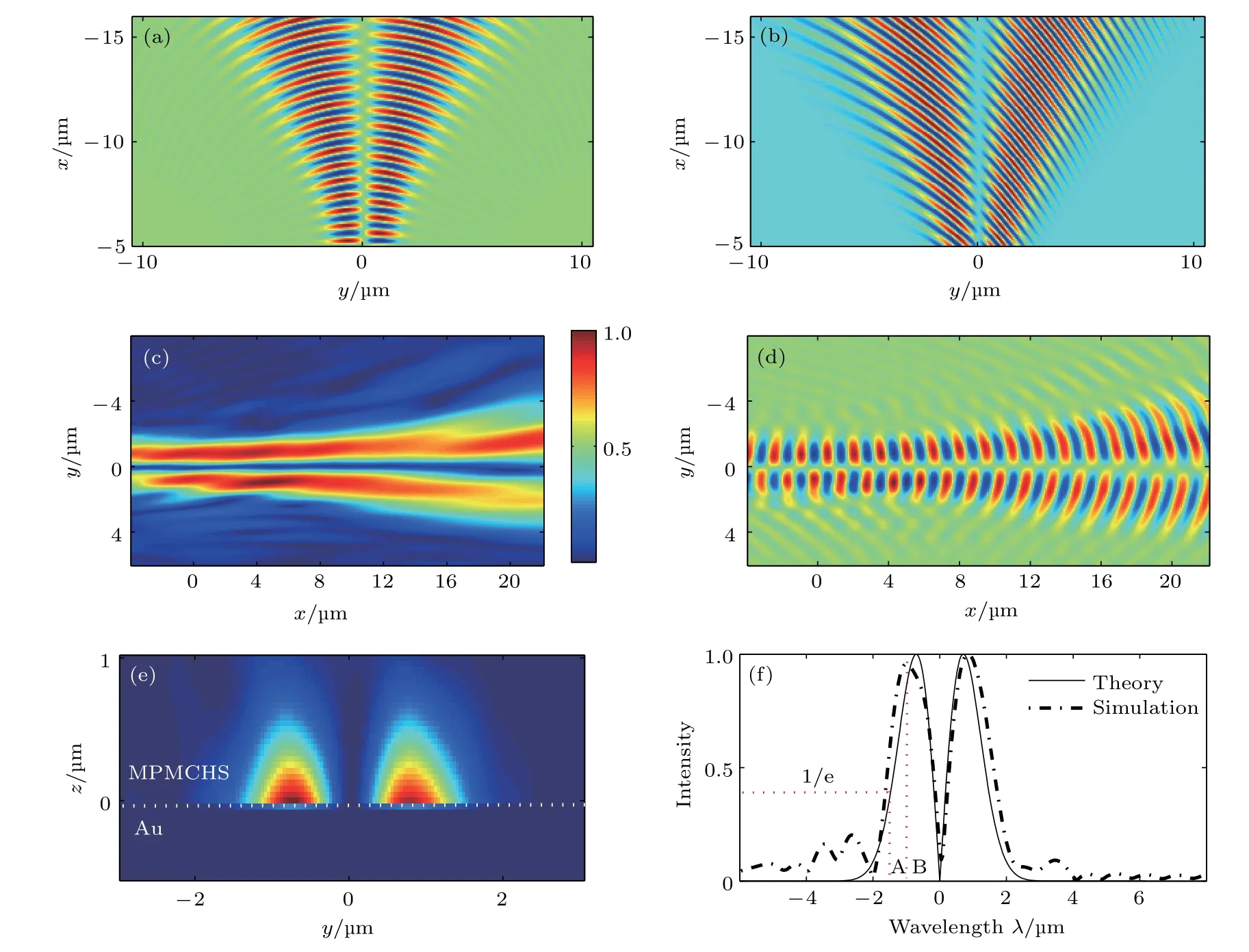
这里r为结构区域内点的位置矢量,r0为物点的位置矢量. 物波与参考波干涉,在−11 μm 本文利用时域有限差分(finite difference time domain,FDTD)法模拟全息图的再现过程. 在模拟中,将模拟区域划分为 Δx=Δy=10 nm 的单元格子. 波长为λ0=1.064 μm束腰半径为 4μm 的高斯光束从自由空间中入射到金属表面的光栅上,激发SPP 高斯波束沿着–y方向传播. 此SPP 高斯光束波前是直的,几乎等同于SPP 平面光束,因此能够扮演重建波束的角色读取全息图. 此SPP 波入射到全息结构区域,通过全息图的散射和反射,生成所需的物波. 图2 全息图设计 (a)汇聚SPP 波于1 个点O (8 μm,0) ;(b)汇 聚SPP 波 于2 个 点O 1(8 μm,−2 μm)和O2(8 μm,2 μm)Fig. 2. Designing the photorefractive holograms: (a) Focusing SPP at one pointO (8 μm,0) ; (b) focusing SPP at two pointsO 1(8 μm,−2 μm) andO 2(8 μm,2 μm) . 图3 光折变材料汇聚平面SPP 波到1 个点和2 个点的模拟结果 (a)汇聚到1 个点时xy平面的光强分布; (b)汇聚到2 个点时xy平面的光强分布; (c)汇聚到1 个点时焦面yz平面的光强分布; (d)汇聚到2 个点时焦面yz平面的光强分布; (e)材料厚度对1 个点汇聚耦合效率的影响; (f)材料厚度对2 个点汇聚耦合效率的影响; (g)折射率调制度对1 个点汇聚耦合效率的影响; (h)折射率调制度对2 个点汇聚耦合效率的影响; (i)全息图尺度对2 个点汇聚耦合效率的影响Fig. 3. Simulation results of coupling SPP wave to a point and two points by metal-photorefractive material complex holography structures: (a) Intensity distribution in thexyplane for focusing SPP to a point; (b) intensity distribution in thexyplane for focusing SPP to two points; (c) intensity distribution in theyzplane for focusing SPP to a point; (d) intensity distribution in theyzplane for focusing SPP to two points; (e) influence of material thickness on coupling efficiency for focusing SPP to a point; (f) influences of material thickness on coupling efficiency for focusing SPP to two points; (g) influence of refractive modulation on coupling efficiency for focusing SPP to a point; (h) influence of refractive modulation on coupling efficiency for focusing SPP to two points;(i) influence of hologram dimension on coupling efficiency for focusing SPP to two points. 通过FDTD 法模拟SPP 波入射到图2(a)所示的折射率分布全息图中. 光折变材料折射率调制度设置 Δn=0.06 ,厚度为 3.3 μm 时,模拟得到在金属表面(xy平面)和焦面(yz平面)的光强分布,分别如图3(a)和图3(c)所示. 从图3(a)可以看到,在金属表面O(8 μm,0) 点处出现明显的焦点,这说明所设计的光折变材料全息结构能将平面的SPP 波侧向汇聚于目标点. 考虑材料的厚度和折射率调制度对耦合效率的影响. 耦合效率定义为流过焦面上 2μm×2 μm 区域内的能流与入射进入结构区域内的能流之比. 固定折射率调制度为Δn=0.06 ,当厚度从 2.6 μm增加到 3.5 μm 时,耦合效率的变化如图3(e)所示. 可以看到当厚度为3.3 μm时,耦合效率达到最高,为21%. 固定厚度为h=3.3 μm ,当折射率调制度 Δn从0.02 增加到0.08 时,耦合效率的变化如图3(g)所示. 可以看到折射率调制度 Δn=0.06 时,耦合效率达到最高,为21%. 考察全息图尺度对耦合效率的影响,结果如图3(i)所示. 当其他条件不变,全息图y方向的宽度d从 1 5 μm增大到 2 1 μm 时,耦合效率谱的最大值从15%增加到19%; 当d从 2 1 μm增大到27 μm时,耦合效率谱的最大值逐渐减少,从19%减小到10%. 设计全息结构将平面SPP 波汇聚到2 个点.在写入过程中,参考波与汇聚到一点时相同,RW=exp(−i·ksp·y). 将此波汇聚到金属表面上O1(8 μm,−2 μm)和O2(8 μm,2 μm) 两点,相应物波的表达式为这 里r1和r2分 别为两个物点O1和O2的位置矢量. 得到在此区域的干涉光强如图2(b)所示. 利用光折变材料将此光强分布转化为对应的折射率分布,即图2(b)是所设计的将SPP 平面波束汇聚于2 个点的光折变材料全息图. 通过FDTD 法模拟SPP 波入射到图2(b)所示的折射率分布全息图中. 光折变材料折射率调制度设置为 Δn=0.06 ,厚度为 3.3 μm 时,在金属表面(xy平面)和焦面(yz平面)光强分布分别如图3(b)和图3(d)所示. 从图3(b)和图3(d)可以看到,在金属表面 ( 8 μm,−2 μm) 和 ( 8 μm,2 μm) 处出现两个明显的焦点,这说明设计的光折变材料结构能将平面的SPP 波侧向汇聚于两个目标点. 固定折射率调制度为 Δn=0.06 ,当厚度从 2.6 μm 增加到 3.5 μm 时,耦合效率的变化如图3(f)所示. 可以看到当厚度为 3.3 μm 时,耦合效率达到最高,为19%. 固定厚度为h=3.3 μm ,当折射率调制度Δn从0.02 增加到0.08 时,耦合效率的变化如图3(g)所示. 可以看到折射率调制度 Δn=0.06 时,耦合效率达到最高,为19%. 下面设计全息结构将平面SPP 波转化为0 阶和1 阶SPP 高斯波束. 沿–x方向传输的0 阶高斯波束在xy平面上的场分布可表达为 其中,w0为高斯波束的束腰半径,束腰位于金属表面x=0 的线上,半径为 2μm. 在区域−15 μm 通过FDTD 法模拟光折变材料全息图的再现过程. 平面SPP 波入射到光折变材料全息图区域内,通过结构的散射和反射,结果如图4(c)—(f)所示. 在金属表面,从图4(c)的光强分布和图4(d)的波阵面分布可以看出,束腰位于x=0 的高斯波束. 图4(e)给出了束腰处的目标波束光强的理论分布曲线和FDTD 法恢复出来的光强分布曲线.从图4(e)可以看出,生成的高斯波束与目标高斯波束分布基本相同,束腰半径都为 2μm ,这证明结构生成了0 阶高斯波束. 图4(f)给出了光折变材料调制度对耦合效率的影响. 这里耦合效率定义为通过束腰处 4μm×2 μm 区域内的能流与入射进入结构区域内的能流之比. 从图4(f)可以看出,当折射率调制度 Δn=0.06 时,耦合效率达到最高,为8.5%. 设计光折变材料全息结构生成1 阶高斯波束.沿–x方向传输的1 阶高斯波束在xy平面上的场分布可表达为 其中束腰半径为 1μm. 在区域−11 μm 图4 零阶高斯SPP 波束的生成,其中图(a)和(b)为物波波面分布、物波和参考光波干涉产生的光强分布; 全息图读出的模拟结果,包括xy平面的(c)光强分布和(d)波阵面分布,(e) SPP 高斯波束束腰处光强分布,(f)折射率调制度对耦合效率的影响Fig. 4. Generation of Gaussian zero-order SPP beam in writing process: (a) Object SPP wavefront; (b) interference intensity distribution between object wave and reference wave. Simulation results of reading process: (c) intensity and (d) wavefront distribution inxyplane; (e) intensity distribution on waist for theory and simulation; (f) influence of refractive modulation on coupling efficiency. 通过FDTD 法模拟光折变材料全息图的再现过程. 平面SPP 波入射到光折变材料全息图区域内,通过全息图的散射和反射,结果如图5(c)—(f)所示. 从金属表面的光强分布(图5(c))和波阵面分布(图5(d))可以看出,生成了束腰位于x=0的1 阶SPP 高斯波束. 图5(e)给出x=0 处截面光强分布,可以看出,表面SPP 束缚于金属表面,远离界面时光强迅速衰减. 图5(f)给出了束腰处的目标波束光强的理论分布曲线和FDTD 法恢复出来的光强分布曲线. 可以看出,生成的1 阶高斯SPP 波束与目标波束分布基本相同,束腰半径都为 1μm . 图5 1 阶高斯SPP 波束的生成,其中图(a)和(b)为物波波面分布、物波和参考光波干涉产生光强分布; 读出过程的模拟结果,包括xy平面内(c)光强分布和(d)波阵面分布,(e)x=0 处yz截面内光强分布,(f)理论和模拟的1 阶SPP 高斯波束束腰处光强分布Fig. 5. Generation of Gaussian first-order SPP beam in writing process: (a) Object SPP wavefront; (b) interference intensity distribution between object wave and reference wave. Simulation results of reading process: (c) intensity and (d) wavefront distribution inxyplane; (e) intensity distribution onyzplane withx=0; (f) intensity distribution on waist for theory and simulation. 本文提出利用金属-光折变材料复合全息结构对SPP 波束的操控. 基于光折变材料工作原理,利用表面全息法在光折变材料中设计结构对SPP 波束进行操控. 在不需要任何刻蚀的情况下制作结构,实现SPP 复杂波面的控制. 利用FDTD 法对设计结构进行验证,结果表明,金属-光折变材料复合全息结构能对SPP 波束进行有效操控,实现了如平面SPP 波束1 点聚焦、2 点聚焦,0 阶和1 阶高斯SPP 波束的生成. 这种控制方法扩展了SPP 控制器件设计和制作方法,也为SPP 的全光控制提供了新的思路,使SPP 全光控制成为可能,进一步实现了SPP 全光开关等功能.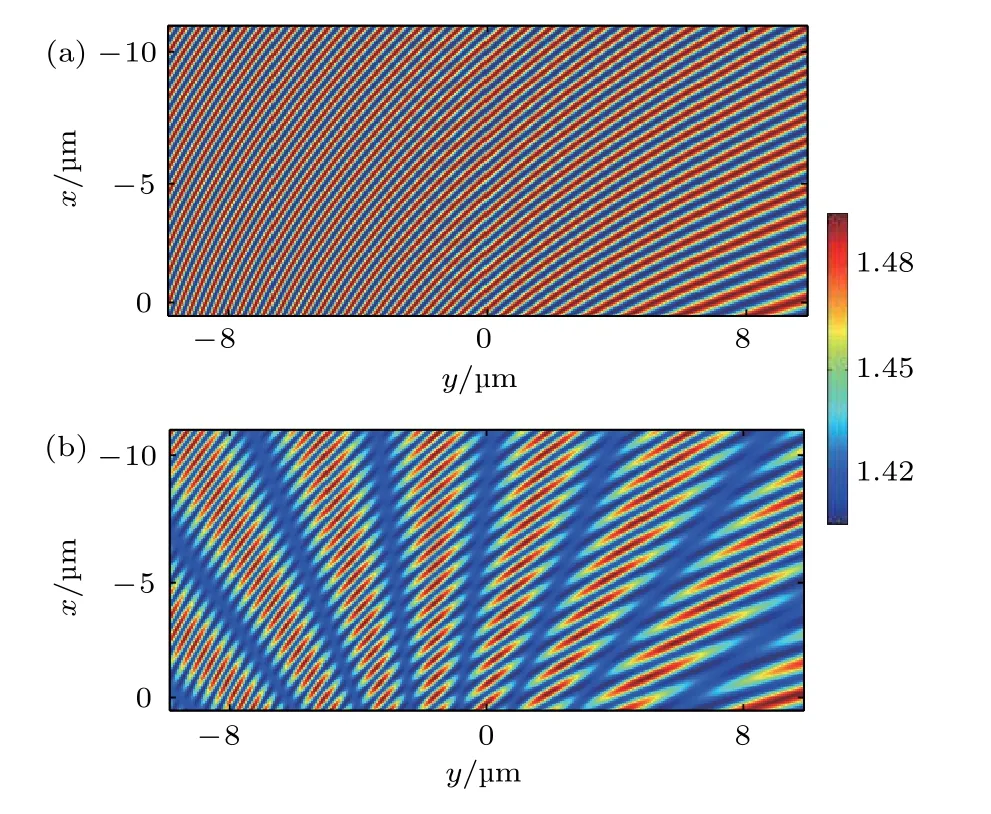




4 结 论

