基于等效夹杂法的多圆孔板平面弹性场研究

张炯，何悦忠，林伟兴，刘卫东，王连坤

（1.五邑大学 土木建筑学院，广东 江门 529020；2.河海大学 机械学院，江苏 南京 210098）

含多圆的孔板广泛应用于建筑、机械和航空航天中，由于圆孔产生的应力集中会大大降低板件的承载能力，从而导致板件在圆孔周围产生破坏，因此研究含多圆孔问题的弹性场分布和其应力集中具有重要的理论和工程实际意义.

针对这一经典问题，学者们进行了大量的研究并提出了相当成熟的计算模型.例如早期的Ling等人[1]运用双极坐标的方法对含两个圆孔的无限大平面进行了分析.后来Savin等人[2]采用复变函数和保角变换的方法对孔洞附近的弹性场分布和应力集中问题进行了研究.高存法等人[3]利用Cauchy积分推导了单个椭圆孔受集中荷载下的通解.李成等人[4]结合弹性理论和复变函数的方法求解了孔边应力场和孔口附近的应力分量.Ting等人[5]利用交替法对无限平面内含多个圆孔的弹性场分布和应力集中进行了研究.

复变函数和保角变换在处理该问题时过程均较为复杂.因此，本文提出了一种基于等效夹杂理论的方法来研究平面内多个圆形夹杂受均匀外载时的弹性场分布，本文方法结合Eshelby内部张量和外部张量，可以简便并准确地求解均布荷载作用下，平面内含任意数量和任意分布的圆孔的弹性场分布.

1 含多圆孔的等效夹杂法

假设在弹性常数为Cijkl的某一无限大板中含n个圆孔，在无穷远处受均匀荷载和如图1所示.

其中，Sijkl为Eshelby内部张量，Gijkl为Eshelby外部张量[6-9].

图1 无限大板含有多圆孔受均匀外载

图2 等效夹杂法变换

结合图1和图2所示的两个等效问题，在夹杂I内建立平衡方程可得：

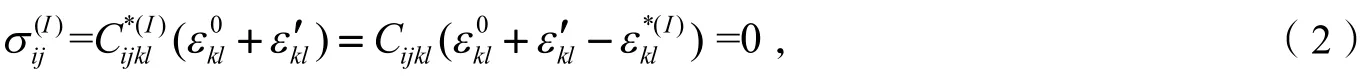
对于平面应变问题，将应变简化为4个未知数：ε11,ε22,ε33,ε12.为了便于计算和编程实现，将式（2）转化为矩阵形式：

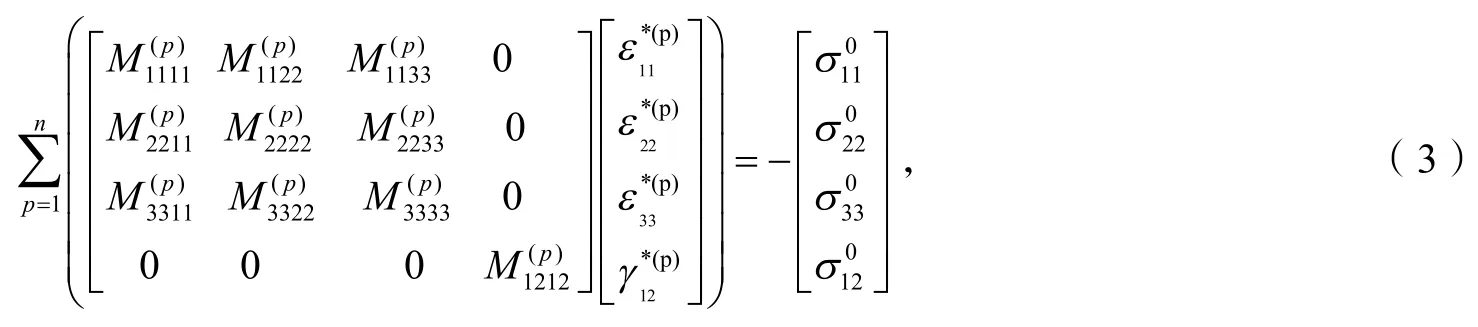
这样，式（3）变为一个含有4个未知数的线性方程组.依次对所有n个夹杂内部都建立平衡后，共可得4n个线性方程组，采用高斯消元法即可求得每个夹杂的等效应变进而求得整个弹性体的应力应变场分布.

2 数值算例

将上述理论利用FORTRAN编程实现，并对相应的典型算例进行分析，同时将计算结果与有限元软件ABAQUS计算结果进行了对比.所有计算都在2.0 GHz和i5 CPU的电脑上进行.

2.1 无限大板含有两个圆孔受单向拉伸载荷

如图3所示：一个无限大板含有两个圆孔，圆孔的半径分别为r1和r2，两个圆孔之间的距离为L，两夹杂圆心连线与x轴所成夹角为θ，无限大板受到竖直方向均匀分布荷载

图3 无限大板含有两个圆孔受单向拉伸载荷

从图4～6可以看出，本文所采用的等效夹杂法与有限元方法所计算的结果吻合十分良好，证明了本文方法的正确性.此外，本文方法在求解该问题时，各点之间是独立求解，并无直接联系；而采用有限元求解时，必须对全局进行网格化分，然后同时求解，计算效率不如本文方法.

图4 Von Mises应力分布（θ=0）

图5 Von Mises应力分布（θ=45°）

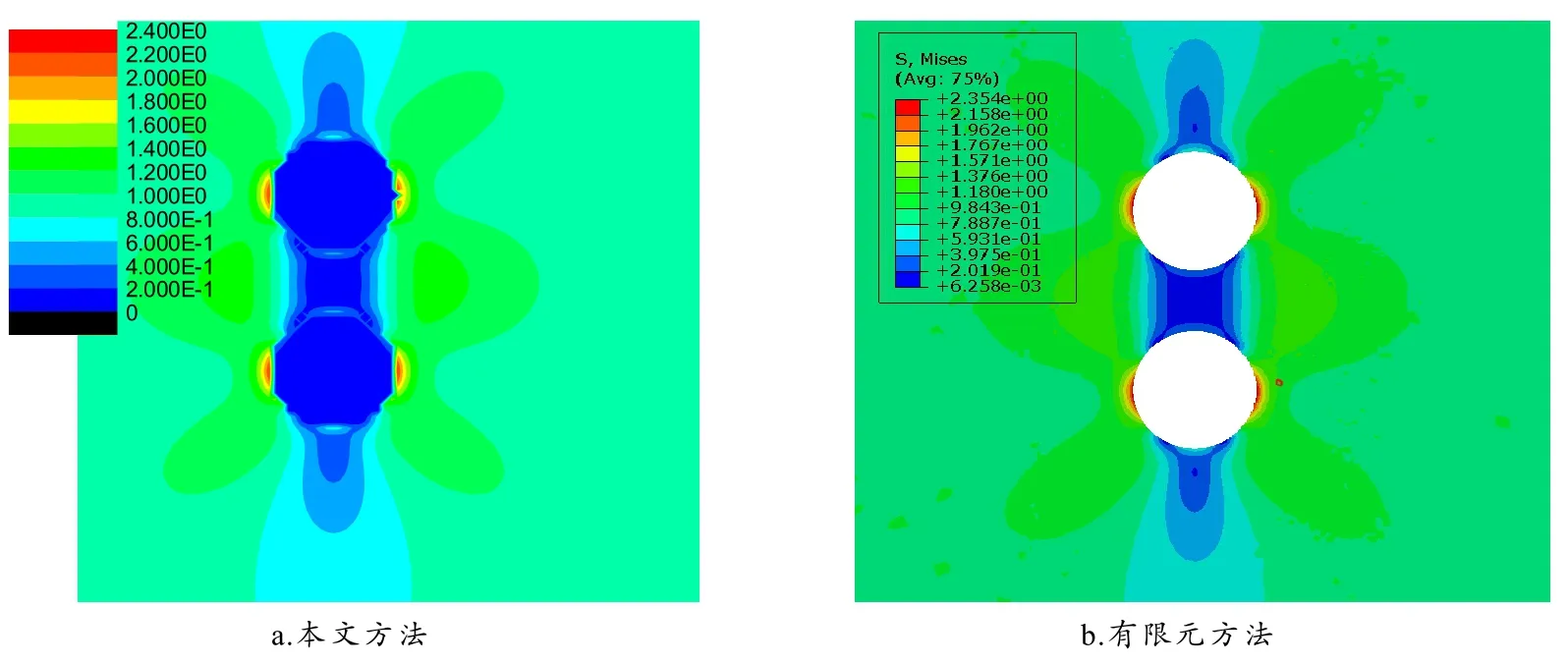
图6 Von Mises应力分布（θ=90°）

下面我们固定r1=r2，研究A点的应力集中系数kt随着L和θ的变化而变化的情况.由于本文方法各点求解相互独立，因此可直接计算A点的应力，计算时间可以忽略，而采用有限元方法计算时，仍然需要对全局进行网格划分并计算出区域内所有的点的应力，计算时间远远超过本文方法.

图7所示的为L=3r1时，A点的应力集中系数kt随着θ的变化而变化的情况，图8所示的为L=3r1时，A点的应力集中系数kt随着L的变化而变化的情况.

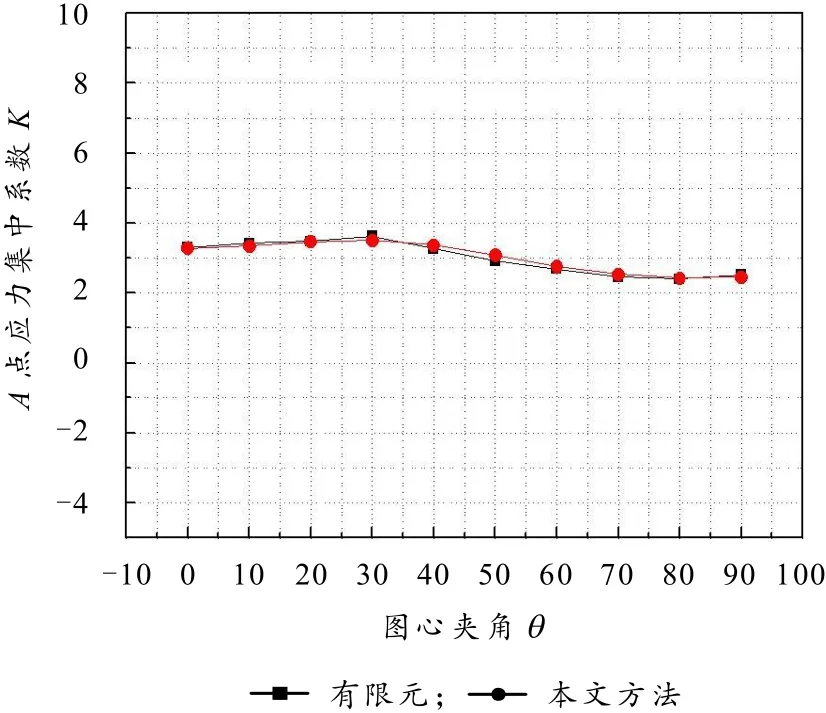
图7 A点的应力集中系数随θ变化

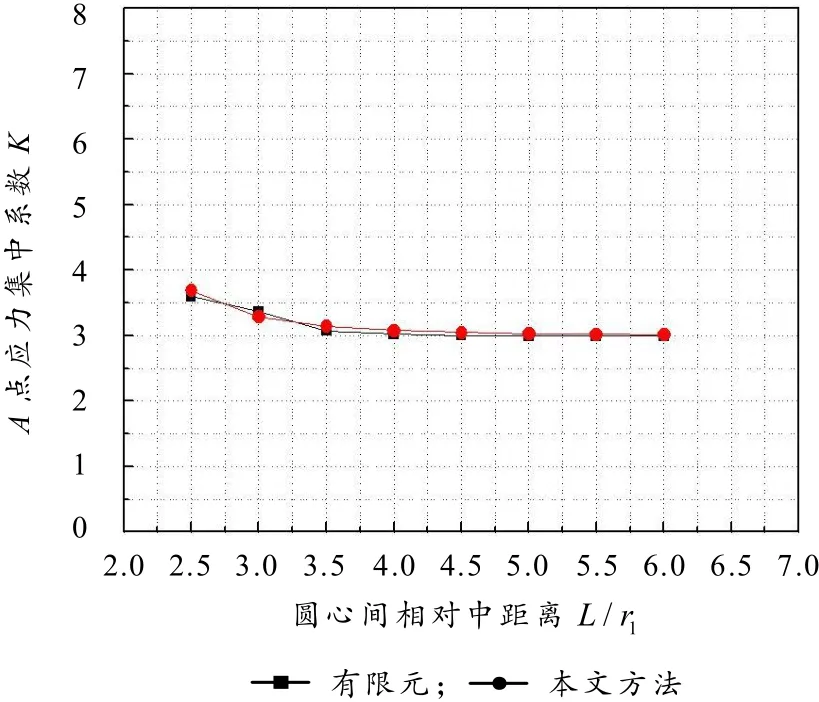
图8 A点的应力集中系数随L/r1变化

从图7～8可以看出，对于A点的应力集中系数，两种方法计算结果吻合十分良好.A点的应力集中系数随着θ的增大先增大，然后减小，最后在θ=90°时，又有增大.从图8还可以看出，当两个圆孔距离很近的时候，圆孔相互影响，应力集中系数接近3.7，随着两个圆孔的距离逐渐增大，圆孔间的影响逐渐减小，最后应力集中系数十分接近3.0，相当于无限大板含单个圆孔的应力集中系数.

图9 无限大平面含有3×3个圆孔受双向拉伸载荷

2.2 无限大平面含有3×3个圆孔受双向拉伸载荷

如图9所示：一个无限大板含3×3个等距分布的圆孔，圆孔间距离为L，无穷远处水平方向受到作用，竖直方向受到作用.

分别采用本文方法和有限元方法计算了夹杂附近的Von Mises应力分布和竖直方向应力σ22，如图10～11所示.

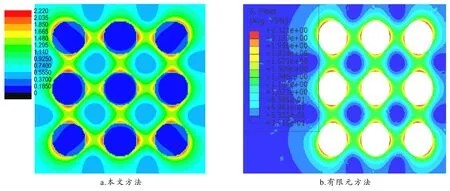
图10 3×3夹杂的Von Mises应力分布

图11 3×3夹杂的σ22应力分布

从图10、11看出，处理多夹杂问题时，本文方法仍然与有限元结果吻合良好.

3 结论

本文通过Eshelby等效夹杂法研究了无限大平面内多个圆孔受均匀分布荷载时的弹性场分布情况.采用了二维圆形夹杂的Eshelby内部张量和Eshelby外部张量对圆孔外的应力应变场进行推导，并采用FORTRAN语言编制了相关计算程序.数值算例表明，本文方法结果准确，与有限元方法相比，可以仅对局部关键部位进行分析，计算效率大大提高.