光刻机工件台解耦矩阵校准测试方法研究
汪杰君,王剑峰,张志钢
(1.桂林电子科技大学,广西 桂林 541000;2.上海微电子装备(集团)股份有限公司,上海 200120)
0 引言
自1973年第一台光刻机在荷兰问世以来,光刻机的伺服精度与日提高,现在已取得了长足的发展[1,2]。光刻机的主要系统包括:光学系统、机械减震系统、测量反馈系统、工件台和掩模台系统等[3]。超精密工件台作为光刻机的3大关键技术之一[4],其要求具有纳米级的定位精度和同步运动精度[5,6]。由于工件台的制造工艺、非质心驱动和测量反馈装置的原因,工件台的实际位置和目标位置存在一定的误差,因而采用合理的测校技术对工件台一些参数进行校准,成为改善其定位精度和同步运动精度的主要手段[7]。
1 光刻机工件台解耦的基本原理分析
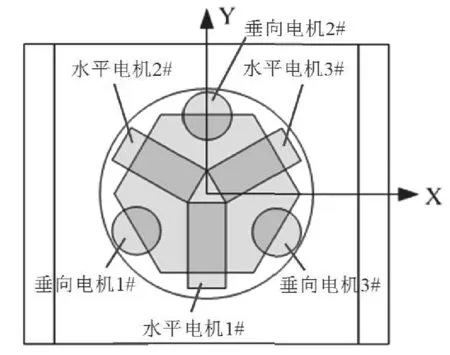
图1 音圈电机布局示意图Fig.1 Diagram of sound coil motor layout
工件台主要由3大部分组成:基础框架、平衡质量块、粗微动台体,微动台是光刻机的核心部件,是微动台进行纳米级运动的关键,刻片时微动台通过调平、调焦等动作,并进行纳米级的曝光运动,使硅片晶圆完整。微动台按功能分为4个机构:Chuck部件、执行机构、测量机构、E-Pin部件曝光。Chuck部件主要包括45°微晶镜块和真空吸盘。45°微晶镜块作为反射镜,配合双频激光干涉仪进行高精度测量;真空吸盘用来固定硅片,防止在上下片过程中硅片滑落;另外,Chuck部件装载测量宏微相对位置传感器的磁极,执行机构主要包括微动平面音圈电机本体及垂向音圈电机。执行机构采用3个平面音圈电机实现执行机构动子的水平X、Y向运动以及Rz偏转;采用3个垂向音圈电机实现执行机构动子的垂向Z向运动和Rx、Ry偏转,这样可实现微动台六自由度精密运动控制;另外,台体垂直方向上还安装重力补偿器,用来抵消微动台重力,来减少音圈电机出力,6个音圈电机布局示意图如图1所示。因此,由于微动电机六自由度的存在,并且其结构精密,系统复杂,不可避免地存在耦合现象,且耦合会影响工件台的工作效率、套刻精度。如果不考虑耦合作用来设计控制系统,在实际中往往会带来很大的控制偏差,所以需要对其进行解耦[8,9]。
2 工件台GB解耦矩阵校准的建模分析
2.1 微动台与音圈电机的力学关系解耦分析
如果将微动台看做一个整体,在控制微动台体沿着某个方向平移,或沿着质心坐标系的某个轴做旋转时,需要由控制系统计算出所需要的力或力矩的大小,并能够恰当地控制各个电机,使得它们的合力恰好是所需要的,这样可以对应每个自由度的位移或转角设计各个自由度的闭环控制系统,各自闭环系统的输出其物理含义是对应的力或力矩大小。磁浮平面电机可分为6个物理轴,分别为H1,H2,H3,Z1,Z2,Z3,它们的相互作用可使电机产生6个自由度的运动。其中,物理轴H1,H2,H3产生水平X向和Y向运动,Z1,Z2,Z3产生垂直Z向运动,水平向和垂直向的相互作用产生旋转运动。当电机在X向和Y向出力时,存在从控制中心到质心点的增益规划和从质心点到执行器的增益平衡。工件台微动台在质心坐标系下和几何坐标系下的受力模型如图2所示。
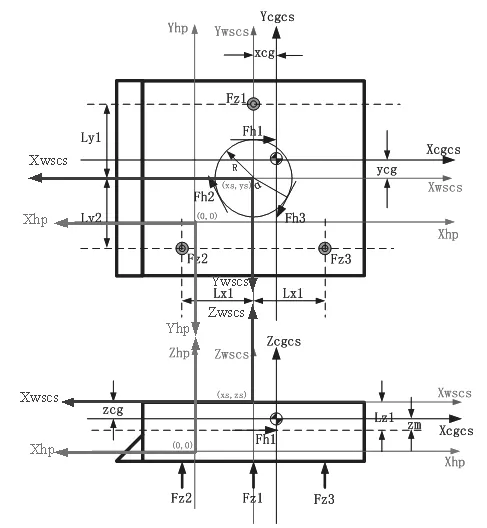
图2 微动台质心坐标系下的微动台受力示意图Fig.2 Diagram of the force of the microdynamic table under the centroid coordinate system of the micro-actuator
Fh2和Fh3与X轴的夹角为60°,3个水平向矢量电机内切圆半径为R,Fh2与内切圆切点、内切圆圆心和微动台质心3点共线。从图2可以得出,磁浮平面电机动子在水平向由3组三相线圈驱动,实现X,Y,RZ三自由度运动。其中,力Fh1和Fh2,Fh3实现X和Y向驱动,Fh1和Fh2,Fh3差动实现RZ的运动。垂向由同样3组三相线圈驱动,实现Z,Rx,Ry三自由度运动。其中,FZ1,FZ2,FZ3实现Z向驱动,Fh1和Fh2,Fh3,FZ1,FZ2,FZ3差动实现Rx向和Ry向驱动。对于平面电机动子质心处的逻辑力及力矩同物理轴各电机驱动力关系可如公式(1)所示:
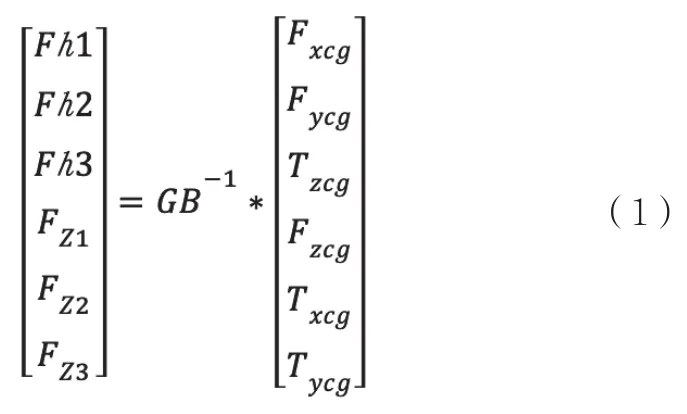
GB逆矩阵如公式(2)所示:
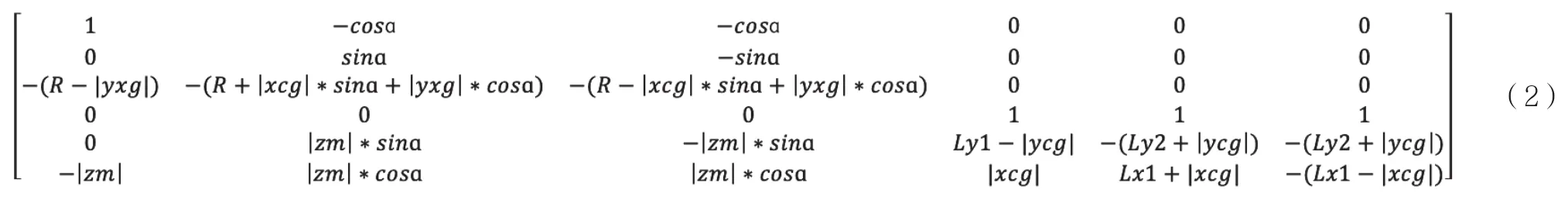
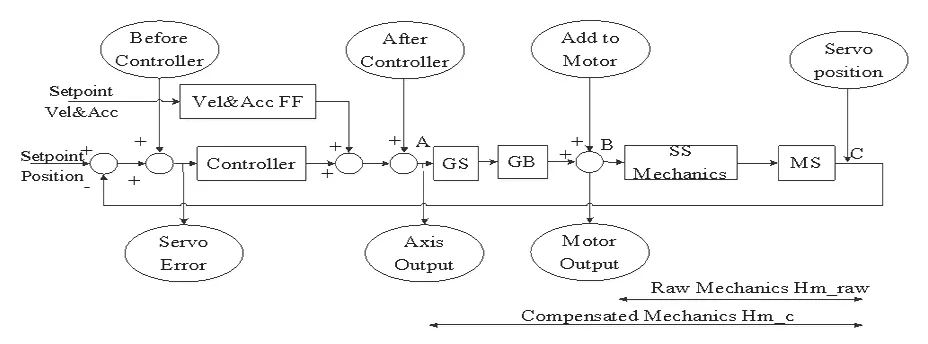
图4 MIMO系统的控制器模块图Fig.4 Controller module diagram of MIMO system
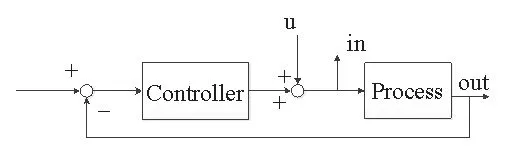
图3 短程电机输入输出Fig.3 Short-range motor input and output
GB逆矩阵参数配置只能用于工件台的理想模型,实际上由于制造误差,如果要求高控制性能,这个矩阵不准确,只能用作默认设置。该矩阵的36个元素均需要进行校准。
2.2 GB解耦矩阵校准算法研究
2.2.1 过程传函计算方法分析
GB解耦矩阵的作用是将逻辑轴控制器的输出力转换到各个物理轴上。SI表示输入敏感度传函(输入为u,输出为in,见图3),SP表示过程传函(输入为u,输出为out,P表示in和out之间的传函),则in和out处的输出分别为:

由式(3)、式(4)可得:

2.2.2 机械传涵计算方法分析
工件台伺服控制环路描述如图4所示。
由图4可知:Raw Mechanics表示B点到C点之间的过程传函,Compensated Mechanics表示A点到C点之间的过程传函,A点到B点之间的过程传函即为GS矩阵与GB矩阵的乘积。因此,GB矩阵可通过计算Hmraw(原始机械传函)、Hmc(补偿机械传函)和GS矩阵来获取。
1)计算机械传函
利用2.2.1所描述的过程传函计算方法可分别计算Hmraw和Hmc。
原始机械传函与补偿机械传函的关系如下:
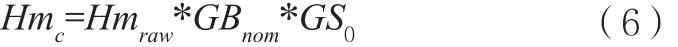
其中,GBnom为校准前的GB矩阵。
2)计算理想机械传函和GS0矩阵
校准后补偿机械传函应该等于一固定的传函Hmd
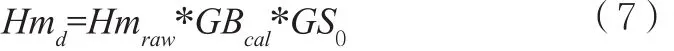
其中,GBcal为校准后的GB矩阵,Hmd和Gs0(Gs0表示工件台处于零位时微动台作用点与质心之间的转换关系)计算公式如下:
Gs0为:

其中,xstep、ystep、zstep为工件台在原点时名义重心相对测量点的位移,xcog、ycog、zcog为工件台在原点时名义重心相对实际重心的位移,其具体值由机器常数给定。
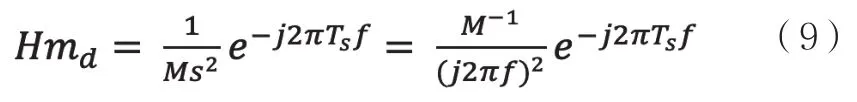
其中,M为:
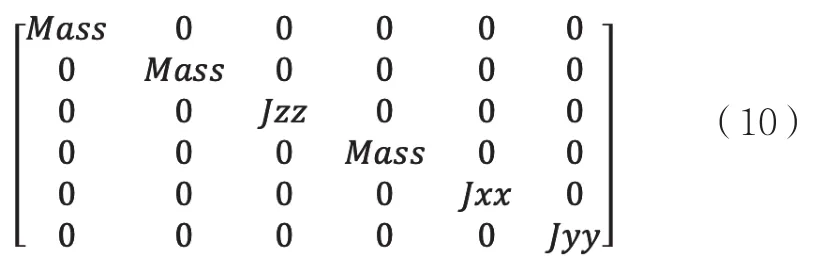
其中,Mass为Chuck质量;Jzz为Chuck绕Z轴旋转的转动惯量;Jxx为Chuck绕X轴旋转的转动惯量;Jyy为Chuck绕Y轴旋转的转动惯量;Ts为采样周期。
3)计算GB矩阵
当原始机械传函确定后,校准后的GB矩阵可表示为:
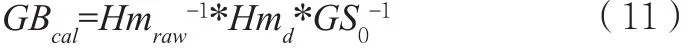
由式(7)和式(11)可得GB的校准公式如下:
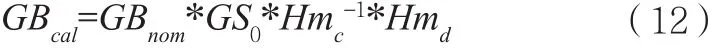
且GB校准矩阵需取某一频率段的均值,该频率范围是[20Hz,50Hz]。
3 实验数据分析
校准前,通过机器常数获取的GB矩阵的值为:
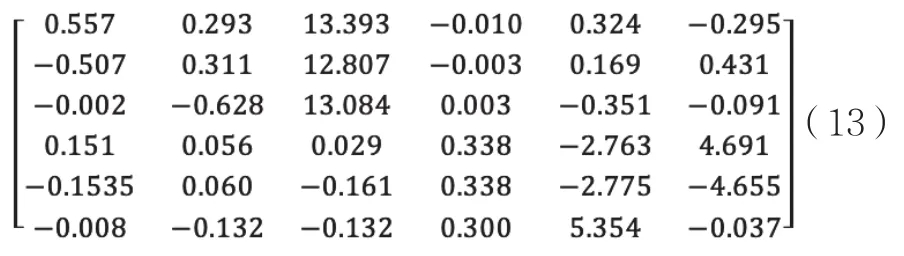
校准后的GB矩阵,如式(14)所示:
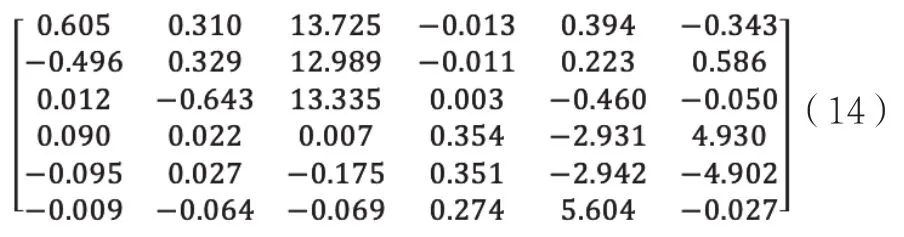
在频域上进行分析测试。
如图5所示,当对X轴注入噪声,噪声水平为20Hz~50Hz时,校准后的机械传涵幅值大幅度降低,即GB解耦矩阵校准后,X方向对RY方向的串扰显著降低。
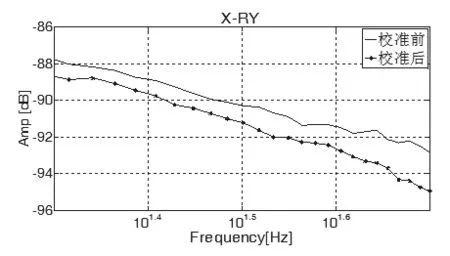
图5 X轴注入噪声,在RY方向上校准前后的串扰对比Fig.5 X-axis injection noise, crosstalk contrast before and after calibration in RY direction
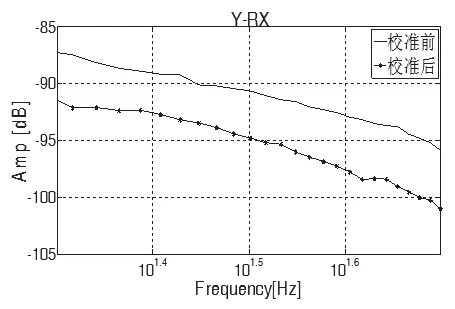
图6 Y轴注入噪声,在RX方向上校准前后的串扰对比Fig.6 Y axis injection noise, crosstalk contrast before and after calibration in RX direction
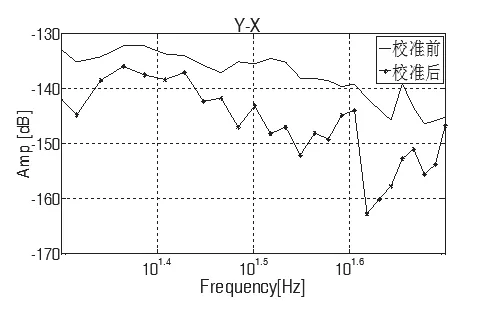
图7 Y轴注入噪声,在X方向上校准前后的串扰对比Fig.7 Y axis injection noise, crosstalk comparison before and after calibration in X direction
如图6所示,当对Y轴注入噪声,噪声水平为20Hz~50Hz时,校准后的机械传涵幅值大幅度降低,即GB解耦矩阵校准后,X方向对RY方向的串扰显著降低。
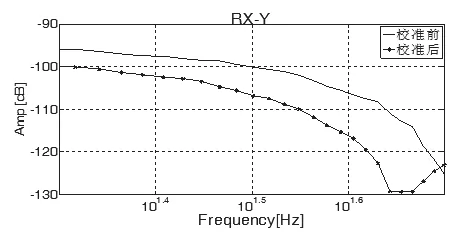
图8 RX轴注入噪声,在Y方向上校准前后的串扰对比Fig.8 Rx axis Injection noise, crosstalk contrast before and after calibration in Y direction
如图7所示,当对Y轴注入噪声,噪声水平为20Hz~50Hz时,在X方向上校准后的机械传涵幅值明显降低,即GB解耦矩阵校准后,Y方向对X方向的串扰显著降低。
如图8所示,当对RX轴注入噪声,噪声水平为20Hz~50Hz时,在Y方向上校准后的机械传涵幅值明显降低,即GB解耦矩阵校准后,RX方向对Y方向的串扰显著降低。
如图9所示,当对Z轴注入噪声,噪声水平为20Hz~50Hz时,校准后的机械传涵幅值大幅度降低,即GB解耦矩阵校准后,Z方向对RX方向的串扰显著降低。
4 结论
本文主要研究工件台微动台GB解耦矩阵的测校方法。根据工件台结构特点,分析得出六自由度之间的耦合会影响工件台的工作效率、套刻精度,在微动台与音圈电机的力学层面分析, 给出了具体的解耦关系式,然后对微动GB解耦矩阵校准方法进行了研究。从工件台的伺服控制环路上的机械传涵为出发点,设计了传递函数法对微动台GB解耦矩阵校准方案,根据最终测试数据,频域上分析得出工件台微动各轴之间的串扰有着明显降低,很好地满足了课题的需要,验证了方法的有效性。
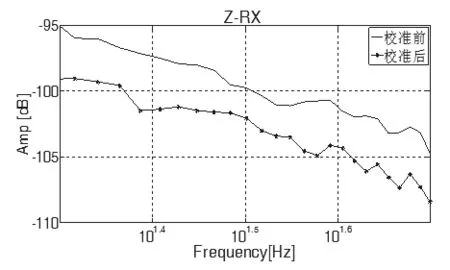
图9 Z轴注入噪声,在RX方向上校准前后的串扰对比Fig.9 Z axis injection noise, crosstalk contrast before and after calibration in RX direction

