高精度平面光栅尺测量系统的模型设计与安装误差分析
郑弘毅
(桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004)
0 引言
根据《国家中长期科学和技术发展规划纲要》部署,中国要在28nm的高端光刻机的研发领域取得重大突破。光刻机的精度一直是光刻机研发的技术难点,而光刻机的测量系统是光刻机精度的关键环节。目前,在工程上光刻机的测量系统使用的是干涉仪测量系统,而干涉仪的测量受环境影响大,且抗干扰能力差。因此,未来将使用鲁棒性更好的平面光栅尺替代干涉仪测量。平面光栅尺已有一些研究应用在光刻机掩模台的位置测量,而在双工件浸没式光刻机的研究和应用目前处于空缺的状态。

图1 平面光栅尺测量原理Fig.1 Measurement principle of plane grating ruler
本文根据平面光栅尺的测量原理,针对目前的28nm浸没式光刻机的双工件台设计了相应的测量模型,并对影响模型的安装误差进行了约束分析与仿真,为实际的工程应用提供了有力的理论指导。
1 模型设计
工件台测量系统模型是根据平面光栅尺获取的莫尔条纹数,计算出光斑的位移,并通过坐标系的转化关系,将光斑的位移转化为工件台的位置信息,以此实现对工件台位置的精密测量。
1.1 测量系统原理
如图1所示,平面光栅尺测量系统由双频激光器、光栅、光栅尺读头和信号接收与处理部分组成。从双频激光器发射出来的激光分为两束,一束作为参考信号,另外一束用于测量工件台的位移。
测量光束以一定的角度出射到光栅的光学面,并发生衍射,当入射光角度满足Littrow角时,会使得光束的+1级衍射光沿原路返回至读头,再经由读头内部角隅棱镜反射,作为二次出射光束在光栅光学面发生二次衍射,并同样沿原路返回至读头;接收器中的光电转换器将入射到其上的测量信号转换为交流电压信号,之后通过相关电路将交流电压信号转换为具有与测量信号拍频一致的方波电压信号,并传输给激光计数轴卡;最后激光计数轴卡进行电学细分和计数,即可获得测量信号的莫尔条纹数。
1.2 坐标系的定义与转化
对工件台位置信息刻画时,需要建立对应的坐标系:
1)工件台坐标系
工件台坐标系是刻画工件台运动的坐标系,其原点位于工件台中心,坐标轴Y轴与平面光栅尺的X向栅格方向成45度角,X轴与Y轴垂直,Z轴正方向竖直向上,三者满足右手坐标法则。

图2 工件台平移和旋转示意图Fig.2 Sketch of table translation and rotation
2)零位坐标系
零位坐标系是工件台位置全为零时的工件台坐标系,是一个基准(框架)坐标系,该坐标系一旦建立,空间上不会改变。
如图2所示,当工件台运动后,工件台除了会产生平移外,还会产生旋转倾斜角。设工件台上任意一点的位置的向量表示为:XWSCS=(x, y, z)T,同一点在零位坐标系下的描述为:XWSCS=(x', y', z')T,从工件台坐标转换到零位坐标满足:

其中,X0为工件台坐标系下当前工件台位置向量,S为旋转变换矩阵,定义旋转倾斜顺序分别为:绕z轴旋转Rz→绕x轴旋转Rx→绕y轴旋转Ry,则SRzRxRy=SRz·SRx·SRy。
1.3 位置测量模型
位置测量模型是描述平面光栅尺输出的条纹读数与工件台位置信息之间关系的表达式,而平面光栅尺测量的位移量是衔接这两者关系的桥梁。
1)位移与条纹数关系
平面光栅尺输出的条纹读数是反映测量光束相位变化的计数值,根据光栅的衍射原理,可得相位与位移之间的表达式为:

而平面光栅尺通过检测出莫尔条纹数,从而得出相位变化,继而可推得位移。
2)位移与工件台位置关系
平面光栅尺测量的位移是工件台发生运动前后,描述的是光斑的位置变化,该位置的变化包含工件台的位置信息。

图3 工件台光束几何关系Fig.3 The geometrical relationship of the beam on the worktable
如图3所示,定义在工件台坐标系,零时刻下,光束出射位置p0的方向向量为np0,SRzRxRy0为零时刻下的工件台旋转矩阵,ws0为零时刻下的工件台位置,则由坐标转化关系得到在零位坐标系下:
出射点位置:

光束出射方向向量:

由点面相交方程,nm为光栅平面的法向量,m=(0,0,h)为光栅平面经过的任一点,可计算出零时刻光斑位置:

同理可得工件台运动后光斑位置:
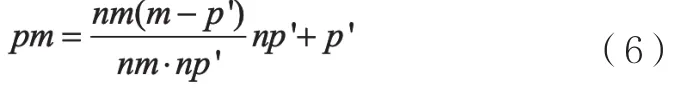
其中,p'工件台运动后光束出射点的位置,np'为定义在零位坐标系下的读头光束方向向量。
tm为光栅的测量方向向量,则光斑在光栅测量方向的位移:

在工件台的运动范围内,由公式(1)与公式(7),根据4个读头的测量值,可得莫尔条纹数和工件台位置的关系。
2 安装误差分析
平面光栅尺测量系统模型的误差主要来源于安装误差。为保证测量模型能够实现对工件台位置的高精度测量,需要对安装误差进行约束,从而指导工程上的安装制造。

图4 工件台安装误差Fig.4 Workbench installation error

图5 安装误差约束Fig.5 Installation error constraints
2.1 安装误差种类
如图4所示,在平面光栅尺测量系统的安装过程中,会存在不可避免的安装误差,其中包括光栅的旋转和平移误差及读头的旋转平移误差。平面光栅尺测量系统是利用光的衍射原理进行测量,光栅的平移误差对其精度影响较小。因此,主要对光栅的旋转误差、读头的旋转误差和读头的平移误差进行分析。
2.2 约束方法
安装误差是不可避免的,对于测量系统模型而言,安装误差越小越好,但在工程实际上,越小的安装误差意味着越高的工艺难度,所以侧重于分析安装误差对模型精度影响的程度,并定量给出在一定模型精度的指标下,可以接受的最大安装误差的大小。
利用三维图对安装误差的约束方法进行说明,如图5为三维图中X轴与Y轴所形成的二维平面图,X与Y分别代表一种安装误差,三维图中的Z轴表示在X与Y安装误差影响下的测量系统模型精度的大小。

图6 测量系统模型仿真方法Fig.6 Modeling and simulation method of measurement system

图7 光栅旋转与读头旋转影响模型精度结果Fig.7 Grating rotation and reading head rotation affect model accuracy results
将3类安装误差两两分类作为二维平面中的X轴与Y轴:读头平移误差与读头旋转误差、读头平移误差与光栅旋转误差、读头旋转误差与光栅旋转误差。首先,将误差限定在一个矩形区域进行分析,矩形区域的边界为组合分析中每一类误差的最大值,一般对3类误差估计的最大值设定为±1×10-3m;然后将每一类安装误差的大小从负最大值到另正最大值以1×10-4m的步进间距计算模型误差点,步进距离越小约束出的误差范围就越精确,但运算量也就越大;通过此方式可以得到安装误差对模型影响的三维关系图;从此三维图中可以根据测量模型的设计精度要求,约束出每一类安装误差的矩形约束范围;根据3类安装误差的约束范围,可以得到在相应模型精度要求下,各类安装误差允许的范围大小。
3 模型仿真
如图6为本文设计的测量模型精度的验证方法,使用的仿真软件为Matlab2013a。首先预设安装误差和工件台的运动轨迹,然后通过测量模型逆向解算出条纹数,并以此模拟出测量系统输出的莫尔条纹数,接着将条纹数带入测量模型,解算出工件台位置,最后将模型计算出的工件台位置与轨迹设定的位置做差,输出模型误差的值。
通过设计安装误差的约束方法,对安装误差的估计最大值设定为±1×10-3m,步进间距设为1×10-4m,并通过设计的仿真方式计算出模型误差值,可得到如下3种类情况的仿真结果:

图8 光栅旋转与读头平移影响模型精度结果Fig.8 Effect model accuracy results of grating rotation and read head translation

图 9 读头旋转与读头平移影响模型精度结果Fig.9 The effect of head rotation and head translation on the accuracy of the model
如图7所示,计算结果呈现出一种四角翘起的形状,说明光栅旋转与读头旋转对测量模型有着同样大小的影响,当读头旋转与光栅旋转误差处于设定的极值时,光栅尺测量模型误差出现最大值。当模型设计精度要求为1×10-10m时,所能接受读头旋转安装误差的范围是-1×10-3rad~1×10-3rad与光栅旋转安装误差的范围为-1×10-4rad~1×10-4rad。
如图8所示,光栅旋转与读头平移误差同时增大,光栅旋转误差对测量模型的精度影响比较明显,读头平移误差影响较弱。当模型设计精度要求为1×10-10m时,所能接受读头平移安装误差的范围是-1×10-3m~1×10-3m与光栅旋转安装误差的范围为-6×10-4rad~6×10-4rad。
如图9所示,读头旋转与读头平移误差同时增大,读头旋转误差对测量模型的精度影响比较明显,读头平移误差的影响较小。模型设计精度要求为1×10-10m时,所能接受读头平移安装误差的范围是-1×10-3m~1×10-3m与读头旋转安装误差的范围为-8×10-4rad~8×10-4rad。
综上仿真结果可知,在1×10-10m的设计精度下,读头平移误差范围-1×10-3m~1×10-3m、读头旋转误差的范围-8×10-4rad~8×10-4rad、光栅旋转误差的范围为-1×10-4rad~1×10-4rad,可以满足相应的设计指标。
4 结论
本文设计的平面光栅尺测量模型可实现从平面光栅尺读出的莫尔条纹数得到工件台位置。通过对平面光栅尺测量系统安装误差的分析,提出了一种约束安装误差的方法,在1×10-10m的设计指标下,读头平移误差范围-1×10-3m~1×10-3m、读头旋转误差的范围-8×10-4rad~8×10-4rad、光栅旋转误差的范围为-1×10-4rad~1×10-4rad,可以满足相应的设计指标,为实际的工程应用提供有效的理论依据。

