基于CATIA软件的楔形盾构隧道管片参数化建模与排版

李永明， 张恺韬， 郭哲良， 杨 磊， 阮 军， 张洛瑜

(浙江省交通规划设计研究院有限公司， 浙江 杭州 310011)

0 引言

通用楔形管片具有生产施工简便、施工动态调整方便、有利于隧道轴线质量控制等优点，因此，被越来越多地运用于现代隧道和地下工程建设中。目前，国内外关于通用楔形盾构隧道设计曲线拟合原理和算法的研究较少。戴仕敏等[1]研究通用楔形管片排版中上下左右产生的位移差，采用全圆周错缝拼装的施工方法控制管片质量。王腾飞等[2]通过管片不同排版产生的旋转角度来研究曲线拟合和纠偏。李伟平等[3]、张忠桢等[4]则把管片分为左、右转环，根据隧道曲线半径与盾构管片参数的关系，计算出曲线段所需左、右转弯环的数量，实现曲线拟合。盾构管片排版原理主要分为平面模拟和三维拟合2类。平面模拟算法计算简便，易于操作，但是对隧道曲线拟合度较差。三维拟合则通过计算管片端面位置和方向等参数，对管片环不同拼装角度的试算点进行筛选，从而获取最佳曲线拟合的位姿[5-6]。

BIM技术的快速发展也带来建模绘图软件功能的升级完善，许多软件公司推出了具有参数化绘图、二次开发能力及多模块多功能集成化的软件平台。利用表格数据驱动模型的方法,可以有效地提高隧道工程中系列化产品设计的质量和效率[7]。康卫林等[8]基于CATIA平台实现了隧道洞口等复杂模型的建模，有效地提高了设计效率。

虽然BIM技术在实际工程中的应用尝试越来越多，但是很少能真正把信息参数化的优势发挥出来。因此，本文以达索(法国Dassault公司)CATIA V6软件作为平台，利用参数化实现楔形盾构隧道管片标准库建模；并将隧道曲线拟合原理与绘图软件相结合，通过建立相关公式，编写拼装脚本，尝试利用表格数据驱动模型对盾构隧道全区间管片进行批量拼装。

1 参数化管片建模思路

CATIA是Dassault公司开发的一款三维绘图软件，其所有模型的绘制通常都需要通过可视化的特征树，以及各种可视工具进行参数化设置，以约束模型的几何尺寸和空间位置[9]。

对于几何尺寸相似的构件，可以通过标准件实体建模、零件参数设计的方式实现参数化建模，并在产品模块利用表格数据驱动模型进行定位拼装以达到批量生成的目的[10]。在使用通用楔形盾构管片的盾构区间中，每一段管片环通常都由封顶块、邻接块和标准块3种管片拼装而成，而所有管片环的拼装又只有空间位置的区别；因此，建立不同特征的管片块标准库，再通过软件参数化功能和脚本数据定位拼装就可以快速高效地生成整个盾构区间的管片BIM模型。

1.1 建立管片标准库

在建立管片的参数化三维模型过程中，首先，需要设置基础可变参数，如管片环外径、管片厚度、楔形量、各分块角度和封顶块形式等相关参数；然后，建立三维模型并对其结构尺寸进行参数设置和约束；最终，生成尺寸可根据数据调整的管片标准库。

通用楔形盾构管片封顶块与标准块的BIM标准模型见图1。由于结构尺寸的参数化设置，在修改可变参数后，再选择更新模型，就可以改变管片尺寸。可更改参数包括管片外径、管片厚度、管片幅宽和楔形量。由于分块数量、螺栓孔数量以及各类防水结构形式参数化所需运算量较大，可通过建立不同模板来实现。

1.2 管片环及区间拼装

建立好管片模型后，把各种管片模型根据管片环中心角度进行拼装组合，生成单段管片环，如图2所示。通过软件计算盾构隧道曲线拟合所需的坐标位置信息，编写相关公式及脚本。把生成的单段管片环进行批量拼装，完成区间隧道BIM建模。在CATIA V6中先定义参数，建立函数公式，再通过脚本的形式调取已知函数，最终完成数据驱动程序的编译。

图1 管片标准块和封顶块模型

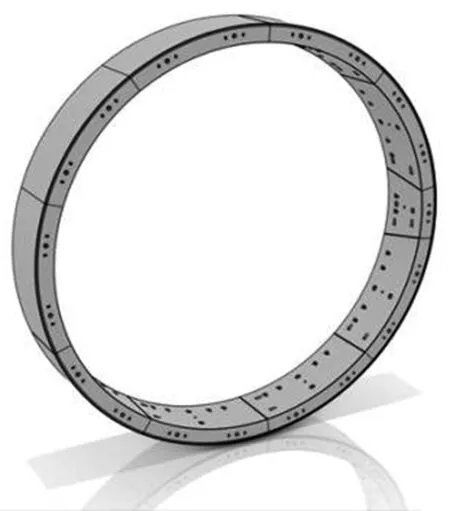
图2 管片环模型

2 隧道曲线拟合原理

盾构区间的设计轴线为光滑曲线，而实际施工中，盾构隧道轴线为各段通用管片环轴线组成的连续折线，因此，施工过程中需对设计曲线进行拟合。每段通用管片环的端面可以分为基准端面和前进面，如图3所示。

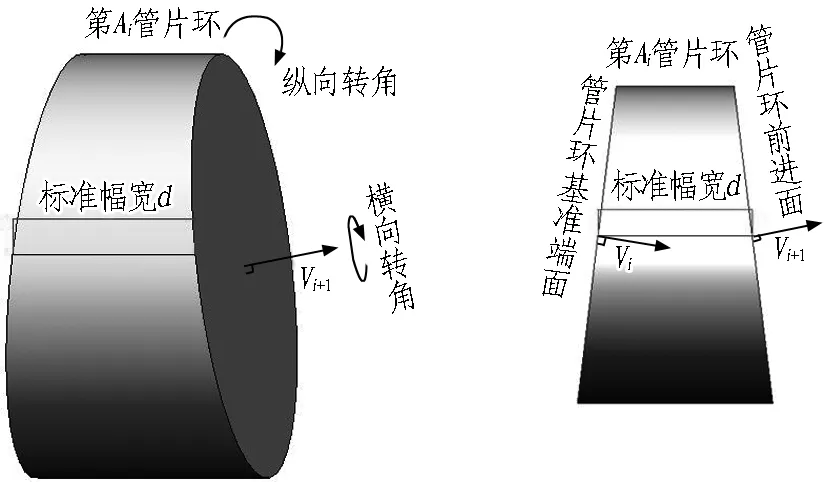
图3 端面向量转换

对于密贴的2个相邻管片环，前一段管片环的前进面所处平面应与后一段管片环的基准端面所处平面相同。每个管片环的位置均可由基准端面的法向量Vi和前进面的法向量Vi+1唯一确定。实际设计中，管片环排版的计算理论就是通过法向量Vi、楔形量产生的轴向旋转矩阵、管片环错缝拼装产生的横向旋转矩阵以及管片环标准幅宽d产生的位移矩阵，用线性代数的方法计算前进面的法向量Vi+1。这种计算理论需要大量矩阵运算，产生较多计算参数。本文利用参数化建模绘图软件CATIA V6的参数化绘图命令，进行几何运算，用绘图软件中的局部坐标系转换代替过去的法向量运算，简化建模以及曲线拟合计算设计理论。

2.1 管片环位姿

通用楔形管片环的拼装位姿参数由其拼装时绕轴线的旋转角度确定。通用楔形管片环的纵向螺栓孔以一定的角度均匀分布，其拼装可选的位姿可看作后一管片环的螺栓孔与前管片环螺栓孔的连接，故位姿数量与螺栓孔数量相等。

若通用楔形管片环设计了n个纵向螺栓孔，则该管片环可以选择的拼装位姿就可以分为n种，其相对于前一管片环位姿的转动角度为(360k/n)°(k=0,1,2,3，…，n)。以含19个纵向螺栓孔的通用楔形管片为例，将楔形管片环上的纵向螺栓孔，从封顶块螺栓开始按0—18顺时针标号。那么，下一管片环的拼装位姿有共计19种可能。以k值表示管片环拼装位姿标号，1号位姿就是后一环封顶块螺栓与前一环1号螺栓相连，如4图所示。图4(a)示出任意环的标号定位，图4(b)示出错缝拼装的2环管片环轮廓，其中，实线为本管片环分块纵向拼装缝示意线，虚线为上一管片环分块纵向拼装缝示意线。

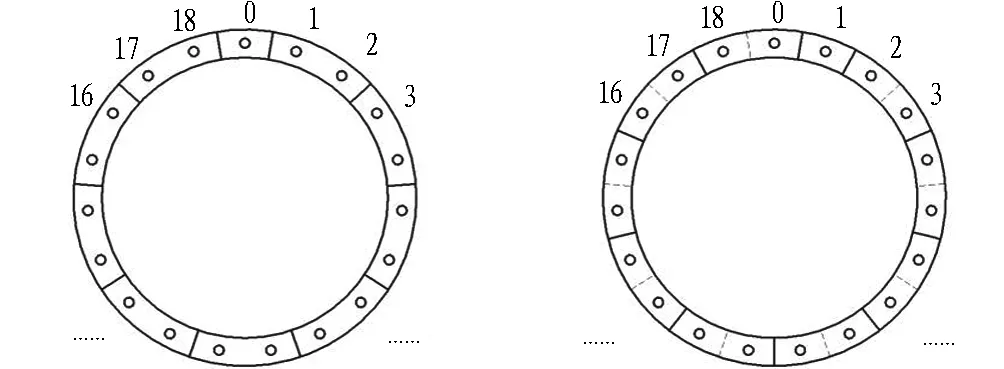
(a) 单环管片分块及螺栓示意图 (b) 管片错缝拼装示意图

图4管片拼装位姿编号示意图

Fig. 4 Demonstration of sequencing segment assembling posture

值得注意的是，由于拼装方式会对管片衬砌结构的力学性能及破坏形式产生影响，通缝拼装方式整体刚度小于错缝拼装方式，破坏时迅速失稳，结构破坏更为严重[11]。因此，根据本文的位姿编号方式，只需要通过脚本编辑剔除k为偶数的拼装位姿，就可以避免通缝拼装的不利结果。

另外，封顶块位置对其在相同荷载条件的力学响应及破坏失稳特征具有显著影响，实际施工中应避免封顶块朝下的不利工况[12]。由于本文以x轴的方向作为封顶块的方向，所以需要在拟合结果中剔除局部坐标系x轴方向向下的不利结果。

2.2 坐标系转换

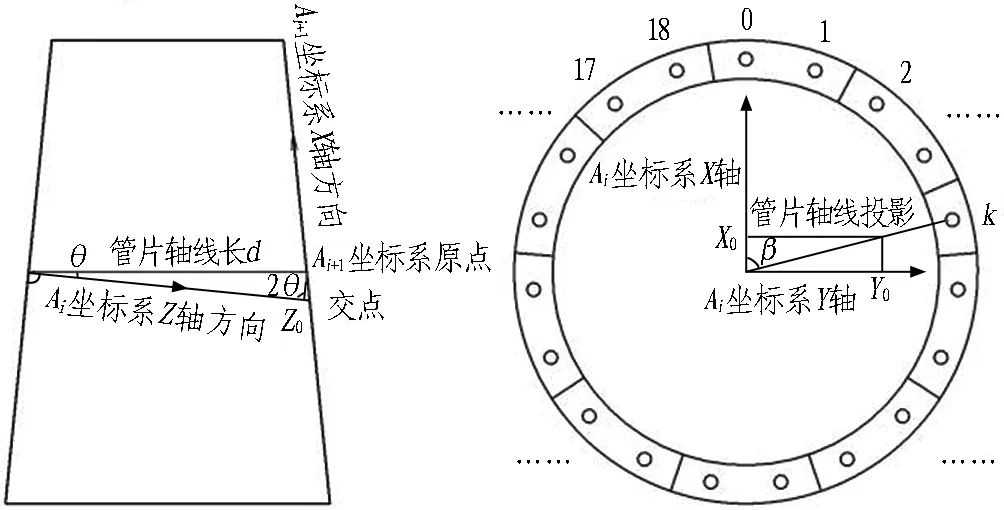
如图5所示，以第i个管片的基准端面中心为原点，内法向量为z轴，基准端面所处平面为xy面的坐标系为Ai；以第i个管片的前进面中心为原点，外法向量为z轴，前进面所处平面为xy面的坐标系为Ai+1，则此管片环的空间位置可以由坐标系Ai与Ai+1的几何参数唯一确定。

图5 坐标系位置示意图

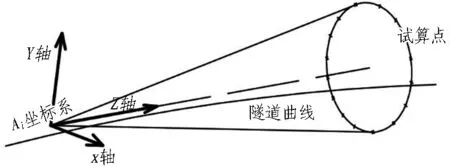
图6 坐标系与试算点几何关系简图

Fig. 6 Sketch of geometrical relationship between coordinate system and trial points

第i个管片的拼装位姿可以与其轴线向量唯一对应，而其轴线向量均以此管片基准端面平面上的Ai坐标系原点出发，并且位于长度为d、与Z轴夹角为Δ/2d(Δ为楔形量)的锥面上，如图6所示。这些位姿对应着第Ai个管片环所有拼装结果，其轴线的末端点位置为曲线拟合的试算点。可以用一系列由位置关系确定的局部坐标系替代管片环拼装的连续折线，而每次拼装坐标转换可以分为2步，如7图所示。由于Ai坐标系与Ai+1坐标系原点分别是基准端面和前进面中心，其位移值即为幅宽d。其中，θ角为管片环轴线(即基准端面和前进面中心连线)与Ai坐标系z轴夹角，根据楔形量值Δ与管片外径D求得。β角为轴线关于Ai坐标系xy平面投影的象限角，可以根据管片拼装位姿编号k与螺栓总数n求得。Ai+1坐标系原点在Ai坐标系下的相对坐标值(X0，Y0，Z0)可表示为

(1)

(2)

Z0=d·cosθ。

(3)

X0=d·cosθ·cosβ。

(4)

Y0=d·cosθ·sinβ。

(5)

(a) 坐标系转换纵剖面 (b) 坐标系转换横剖面

图7坐标系转换计算简图

Fig. 7 Sketch of conversion of coordinate system

确定原点后只需计算该坐标系X轴方向就可确定Ai+1坐标系。每个通用楔形管片环基准端面法向量与该管片环前进面的交点位置是确定的，而该交点与管片环前进面中心的连线方向是指向其封顶环螺栓方向的。故该连线方向就是所需求解的Ai+1坐标系X轴方向。

由于管片环基准端面法向量方向即为Ai坐标系Z轴，位置关系如7图所示，故交点的xy坐标值均为0，交点Z轴坐标为

Zi=d·cosθ·(1+tan 2θ)。

(6)

最后，由所求交点和管片环前进面中心坐标，得到Ai+1坐标系X轴方向，实现坐标转换。

2.3 曲线拟合方式

为了使管片轴线组成的多段线更贴合设计曲线，需要对每种拼装位姿的结果进行试算，找到管片环轴线末端点与曲线距离最近的位姿。通常的做法是，通过最小二乘法，在设计曲线前进方向上寻找与管片轴线起点距离为管片环标准幅宽d的点作为理论中心点，试算各种位姿下轴线末端点的位置，与理论中心点最近的位姿为最佳结果。这种计算方法通常需要通过多步迭代计算理论中心点，且其计算的最佳位姿未必为真正最拟合的结果。

如图8所示，假设在一次计算中，C点为Ai坐标系中点，B点为迭代计算得到的理论中心点，P1、P2分别为2种位姿计算轴线向量末端点，4点均处于同一平面上，线段CB=CP1=CP2=d。如果线段P1B=P2B,则根据过去的拟合原则，P1、P22点对应位姿与曲线的拟合度是相当的。但是，由于设计曲线并不是直线，在此情况下，P1点与设计曲线的距离比P2点与设计曲线的距离更小，即P1点对应的位姿与设计曲线更为拟合。

因此，借助参数化建模软件提供的功能，本文提出直接通过比较管片环轴线末端点与曲线距离的方式筛选最佳管片环位姿，即直接由CATIA软件输出试算点到设计曲线的距离，然后选择距离最小的试算点进行拟合。

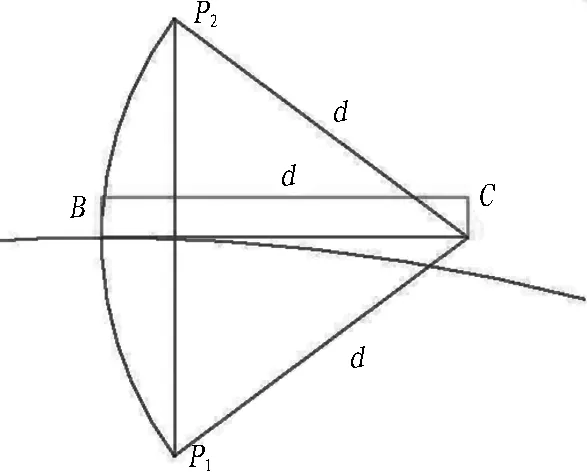
图8 现行试算原理特殊情况

2.4 软件程序流程

由于每环管片环的排版都可以看做是不同初始条件下的相同流程，故可以利用CATIA软件智慧工程模块中的超级副本功能，编写能提取循环步结果并赋值到下一循环初始值的驱动脚本，以完成机械重复的排版过程。

根据排版原理，可以把每环管片环排版的初始条件设置为基准端面所处平面的坐标系Ai，而每环排版流程的输出结果为前进面所处坐标系Ai+1。那么，每步排版流程即为不同初始赋值下的重复循环，分为以下5步： 1)输入初始条件Ai； 2)计算出n个可能的试算点； 3)在试算点中剔除通缝拼装以及封顶块朝下的结果； 4)计算剩余试算点与设计轴线的距离，并取距离最小值的结果； 5)根据选取的试算点结果，计算出前进面所处坐标系Ai+1。

在CATIA软件智慧工程模块，建立以上流程的超级副本，再编写能提取输出结果Ai+1并赋值到下一步初始条件Ai的循环脚本程序，就可以完成脚本建模。由于在轴线上管片环数量应该小于或等于轴线长与管片环幅宽的比值m，本文选用的驱动脚本的循环判断元素为循环步数值。当循环步数小于或等于m时继续下一步循环，反之则跳出循环步，如图9所示。

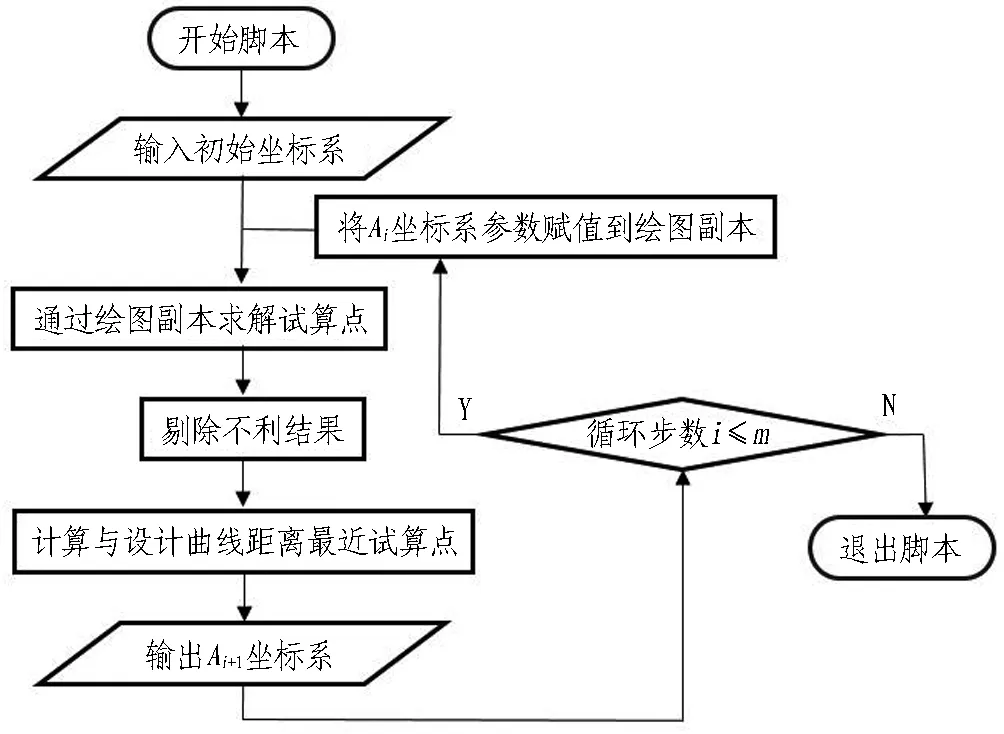
图9 软件内排版程序流程图

3 建模脚本

3.1 坐标转换脚本

Ai坐标下的计算结果参数，赋值到Ai+1坐标系的脚本可由如下命令实现：

myStartPoint=myGeo.Find("Point","x.Name=="StartPoint"",True)

其中，“myStartPoint”为定义的循环初始输入参数，“myGeo”为建模计算的副本。该语句的含义是使用“.Find”命令在“myGeo”副本中调取名为“StartPoint”点的参数计算结果，并复制给“myStartPoint”。类似地，分别在循环内定义坐标原点和X轴，Y轴向量的赋值命令，就能在CATIA软件实现坐标转换的循环。

3.2 剔除封顶块向下脚本

试算点关于初始坐标系的x坐标值最小的结果就是封顶块向下时的位姿，所以，只需要比较x轴坐标值与某一阈值(不同尺寸的管片阈值不同)的大小就能剔除封顶块向下时的位姿。实现脚本如下：

ifmyPoint.coord(3)>=Threshold

myListOK.Append(myPoint)

其中，“myPoint”为试算点结果，用“.coord(3)”函数调取其x坐标值；“Threshold”为定义的阈值，大小应根据管片形式改变；“myListOK”为定义的非封顶块向下的结果列表。逐个筛选试算点，当试算点x坐标值大于阈值时，把该点加入列表。

3.3 求与曲线距离最小试算点

求与曲线距离最小试算点，需要建立循环。通过“distance”命令计算每个试算点与隧道主线“RefMainLine”的距离，并逐个比较距离值大小，最终把结果最小的试算点赋值给“StartPoint”，脚本命令为

for i while iSize()

{

if (distance(DGP_TemRefMainLine,myPoint)/1mm) >(distance(DGP_TemRefMainLine,MyList->GetItem(i+1))/1mm)

{myPoint=MyList->GetItem(i+1)}

}

DGP_TemStartPoint=myPoint

4 拟合分析与工程实例

为了研究可视化管片排版程序的实用性，本文以杭州市艮山快速路下沙段提升改造工程初设中选取的直径为14 m、幅宽为2 m的楔形盾构管片为例。通过40、60、80、100 mm 4种楔形量管片类型，分别对转弯半径为400、600、800、1 000、1 200 m的圆弧总计20种工况进行拟合，获得了软件拟合得到的管片坐标与对应的理论拼装误差结果。

4.1 不同楔形量与转弯半径工况拟合度分析

在CATIA软件完成隧道区间曲线拟合和管片排版模拟后， 输出筛选点坐标结果与每个点对应的拟合误差。根据式(7)—(9)可分别计算出拟合轴线的最大拼装误差Emax、平均拼装误差以及拼装误差的方差。

Emax=max(E1,E2,E3,…,En′)。

(7)

(8)

(9)

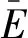
各项工况误差值计算结果如表1所示。其中，以本文选用的直径为14 m、幅宽为2 m的盾构管片实例，40 mm的楔形量对转弯半径400 m与600 m设计曲线进行试算的结果为发散，不能满足400 m与600 m转弯半径的需求；而60 mm楔形量对转弯半径400 m设计曲线的试算结果发散，不能满足400 m转弯半径的需求，故而其拟合结果未列出。

由表1计算结果分析，可得出以下结论：

1) 在盾构管片半径和幅宽确定的情况下，设计隧道曲线转弯半径越大，其拟合的理论误差通常越小。

2) 对于确定的转弯半径，设计的楔形量不能过小，否则可能无法满足转弯半径的需求。在一定范围内，过小的楔形量在拟合过程中容易出现曲线转弯方向与拟合线路的转向不同，需要多步修正，造成拟合线路的误差方差巨大。如表1所示，80 mm楔形量在400 m半径曲线的拟合方差，以及40 mm楔形量在800 m半径曲线的拟合误差方差都超过了100 mm。

3)在楔形量能满足转弯要求的条件下，试算每种转弯半径工况的楔形量得到转弯半径的最优选择。通常楔形量不宜过大，如在800、1 000、1 200 m的工况下，100 mm楔形量的管片试算误差较80 mm与60 mm楔形量的管片误差更大。

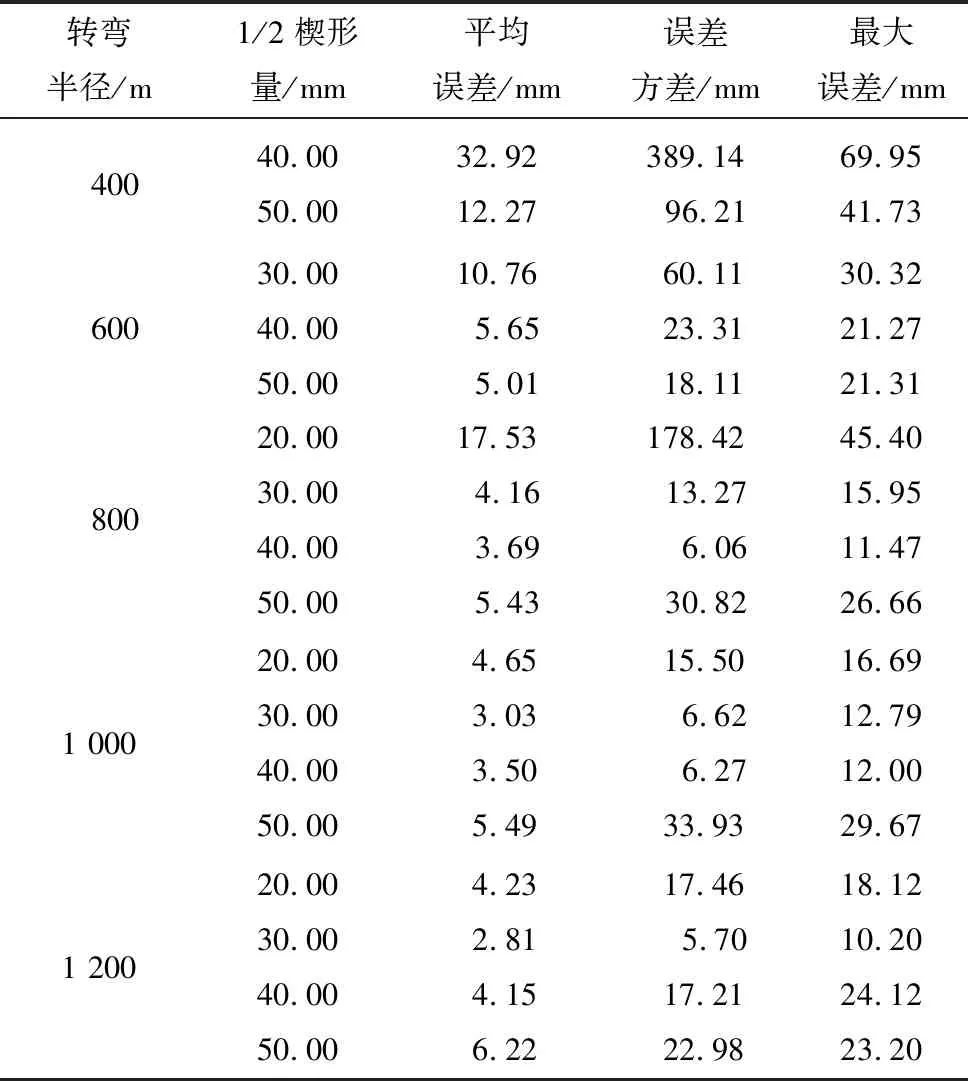
表1 各项工况误差值计算结果

4.2 实际设计曲线拟合结果

艮山快速路下沙段提升改造工程隧道全长5 577 m，盾构区间长度为1 603 m，通过拟合其初设曲线，圆弧段最小转弯半径为610 m，其余区间均为缓和曲线与直线段，盾构平面线位如图10所示。

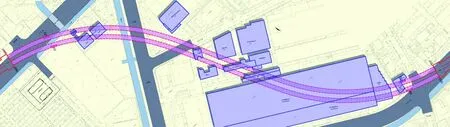
图10 盾构区间平面线位

将设计线路导入排版程序，可知60 mm楔形量的拟合误差较小。因此，本文使用60 mm楔形量管片排版结果进行管片拼装模拟。为了方便施工中管片位姿的确定，把管片环中各管片用不同颜色表示，并在CATIA中完成可视化拼装。如图11所示，用颜色区分相邻块以指导拼装，封顶块为棕色短块。

图11 可视化排版拼装结果

5 结论与讨论

本文以达索的CATIA V6软件作为平台，建立楔形盾构隧道管片标准库，实现参数化建模；并将隧道曲线拟合原理与绘图软件相结合，建立相关公式，编写拼装脚本，实现盾构隧道全区间管片的批量拼装；通过对比不同楔形量与转弯半径的拟合计算结果，分析楔形量对拟合结果的影响，并通过对实际工程设计曲线进行拟合计算，为管片设计提供一定依据。

1)运用绘图软件的参数化功能，建立设置几何参数约束的管片标准库，可以提高管片设计信息的准确性，减少设计阶段管片尺寸变更带来的重复劳动，有效提高实际工程的绘图效率。运用三维绘图软件的函数编辑和脚本编辑，可以实现隧道管片排版的可视化拟合。

2)除了实现管片排版拼装外，可根据实际工程设计曲线对不同楔形量尺寸进行多次试算，分析计算结果，找到理论上更符合设计曲线的管片尺寸数据，为实际工程提供依据。

现有的管片拟合原理中，每环管片的定位都是基于上一环管片的计算结果取误差最小的分步解，未必为基于设计曲线全线的最优排列解。因此，基于曲线全线拟合结果最优的拟合方法是值得进一步研究的。