城市浅埋隧道竖井排烟烟气逆流的影响研究

姜学鹏， 吴锦东

(1. 武汉科技大学资源与环境工程学院， 湖北 武汉 430081； 2. 湖北省工业安全工程技术研究中心，湖北 武汉 430081； 3. 武汉科技大学消防安全技术研究所， 湖北 武汉 430081)

0 引言

城市浅埋隧道净高小、长度短，相比传统的机械排烟，国内外一些城市浅埋隧道选择环保、经济的竖井自然排烟方式。通过竖井产生的烟囱效应把烟气排出，利用压强差能够达到较好的烟气控制效果，但影响这种排烟方式效果的因素较多，包括外界风、火源功率、火源与竖井相对位置、竖井几何形状等[1]。

在隧道火灾研究领域，烟气逆流一直是防排烟的研究重点。Hu等[2]通过缩尺寸模型试验，对顶部开孔处设有风机的隧道内烟气蔓延进行研究，提出了基于纵向送风和顶部风机排烟条件下的隧道烟气逆流预测公式。文献[3-4]对铁路隧道烟气运动进行研究，提出铁路隧道烟气逆流长度预测公式。文献[5-7]在缩尺寸模型试验的基础上，通过无量纲分析，得到无量纲状态下烟气逆流长度与火源热释放速率及纵向通风风速的关系。Yao等[8]在文献[2]的基础上，提出虚拟火源的理论，通过构建缩尺寸隧道模型，研究了当竖井在火源上游时，在隧道纵向风和单个竖井的共同作用下，隧道竖井与火源的水平距离对烟气逆流的影响，建立了超出竖井部分烟气逆流预测模型。此外， Takeuchi[9]通过缩尺寸模型试验，建立了竖井自然排烟隧道顶板下方烟气温度分布预测模型。Guo等[10]在缩尺寸试验的基础上研究了大断面竖井下，火源热释放速率、竖井高度和竖井间距对隧道烟气温度和超出竖井部分烟气蔓延长度的影响。

尽管前人对公路隧道火灾烟气逆流进行了大量研究，但针对竖井排烟隧道里火源热释放速率、纵向送风、竖井与火源间距、竖井宽高等因素共同作用下的火源上游烟气逆流的研究较少。受烟囱效应的影响，烟气蔓延至竖井时，竖井处烟气与空气之间存在温差及密度差，在温差和密度差的作用下烟气经竖井排出，如图1所示。在烟囱效应和隧道纵向送风的作用下，竖井对隧道烟气具有一定的引流作用，引导烟气向火源下游蔓延。本文以东湖隧道竖井自然排烟段为工程背景，采用无量纲理论分析，通过数值模拟技术，考虑隧道纵向风的影响及固定火源位置，在不同的火源功率下，改变火源与竖井的间距及竖井宽和高，研究竖井与火源间距、竖井宽和高对隧道火灾烟气逆流的影响，建立竖井排烟隧道内火源上游烟气逆流长度的预测模型。

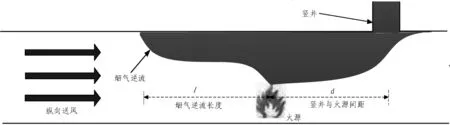
图1 竖井排烟烟气蔓延示意图

1 理论分析

(1)

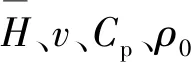
f(π1，π2，π3，π4，π5，π6，π7)=0。

(2)

其中,

(3)

由此方程可求得各参数如下：

(4)

上述无因次方程可列为

(5)

代入式(2)求得

(6)

根据相似理论的相关规则[11]化简，式(6)化简为

(7)

即

l*=f(Q*,v*，d*，h*,w*)。

(8)

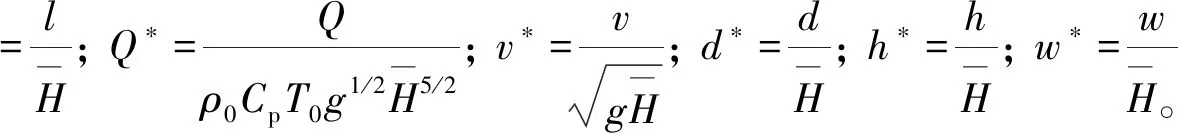
2 数值模拟

2.1 物理模型设置

以东湖隧道为工程背景，建立如图2所示的全尺寸矩形断面隧道数值模型。隧道模型长×宽×高为500 m×13 m×7 m。火源位于隧道纵向中央(尺寸为4 m×4 m)，竖井长7 m位于火源下游，宽、高变化如表1所示。采用FDS 6.1软件进行隧道火灾数值模拟，并在距隧道顶板0.1 m处设置一系列热电偶，相邻热电偶间距0.5 m，以精确确定烟气蔓延位置。

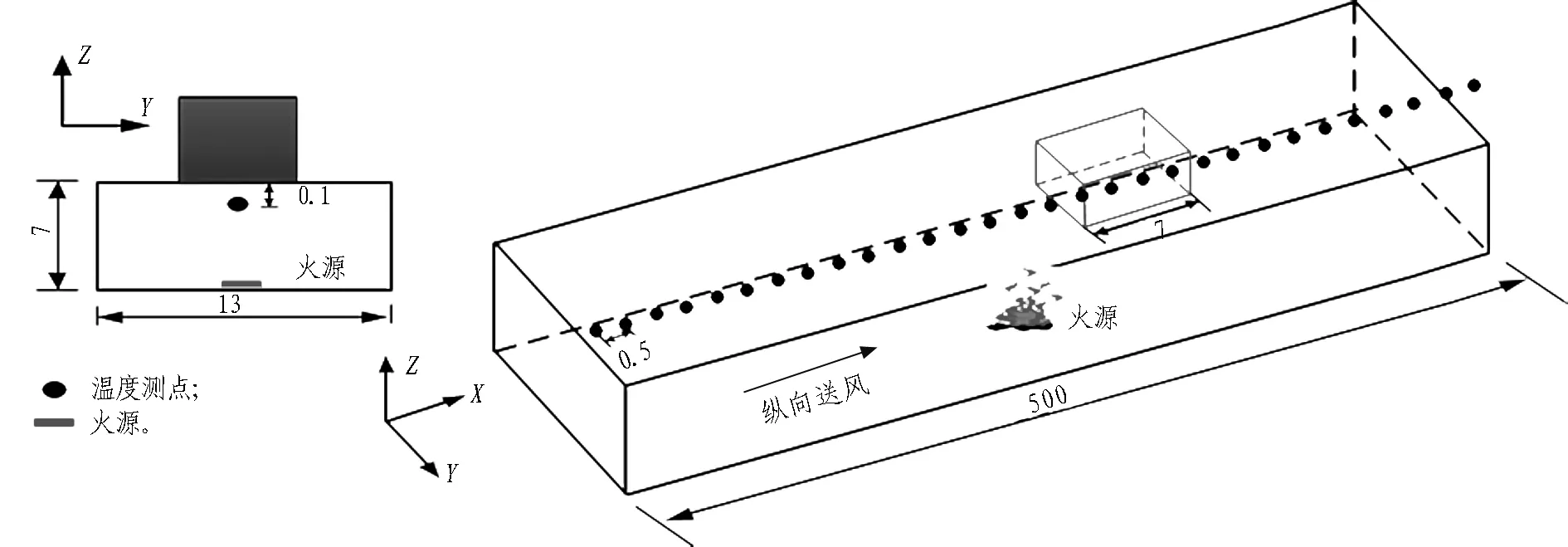
图2 隧道模型简图(单位： m)

2.2 网格独立性分析

为确保模拟精度与效率，FDS网格的长宽比一般不应超过3。Baum[12]通过研究发现在火灾特征直径D*≤0.1 的情况下，FDS软件能够对羽流运动做出较精确的模拟； 祝实等[13]研究认为火源区对于网格密度最为敏感，加密火源区可以在控制计算时间的同时有效提高计算精度。Mcgrattan等[14]提出火源特征直径与网格尺寸比值D*/δ介于4～16以解决网格尺寸的确定问题，被广泛采用，其中，火源特征直径D*计算公式为

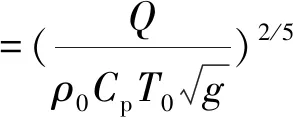
(9)

以10 MW的火源热释放速率为例，其火源特征直径为2.40 m，推荐网格尺寸0.15～0.60 m。不同网格尺寸下隧道同一位置处温度变化对比如图3所示。随着网格尺寸减小，温度曲线趋于一致，但网格尺寸低于一定程度时，尺寸的进一步缩小，时间成本大幅增加的同时温度并未产生明显变化。故隧道整体网格尺寸为0.5 m×0.5 m×0.5 m，对局部区域(火源及竖井附近)进行加密处理，设置为0.25 m×0.25 m×0.25 m。

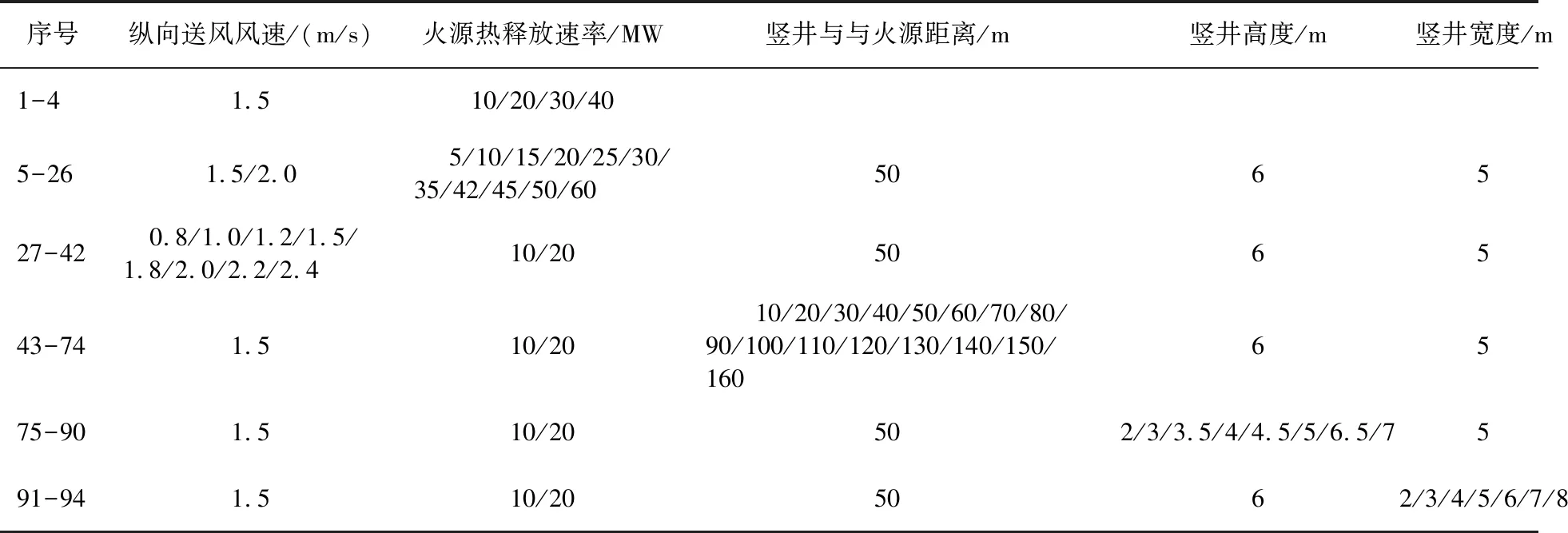
表1 工况设计表

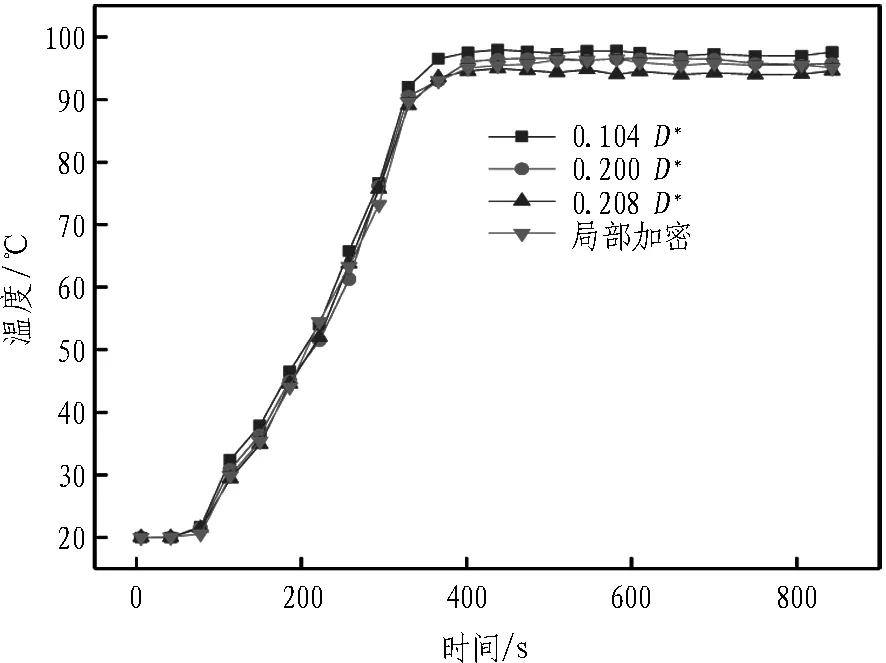
图3 火源下游20 m处温度随时间变化曲线(6.5 m高)

Fig. 3 Time-history curves of temperature 20 m downstream of fire source at height of 6.5 m

2.3 工况设计

依次改变东湖隧道内火源热释放速率、纵向送风大小、竖井与火源间距以及竖井宽、高，共设计94组工况(其中，1-4号为无竖井时的工况)，研究不同因素影响下，竖井排烟隧道发生火灾时上游烟气逆流情况，详细工况设计如表1所示。

3 结果和分析

3.1 烟气逆流

火源热释放速率为20 MW、纵向送风为1.5 m/s、竖井与火源间距为50 m时，隧道顶板下方烟气温度纵向分布如图4所示，它能反映隧道烟气的蔓延情况。通过测量火源上游顶板附近温度可得到烟气逆流长度，因为火源上游逆行热烟流在蔓延时温度会不断降低，与送风冷气流交锋形成1个冷热锋面，前锋面位置存在温度陡降，该温度陡降处与火源之间的距离即为逆流长度[16-17]。

若纵向送风为1.5 m/s，在有竖井和无竖井2种情况下，隧道上游烟气逆流长度如图5所示。在不同火源热释放速率下，有竖井时上游烟气逆流长度均小于无竖井。火源下游竖井通过烟囱效应将一部分烟气排出，一定程度上，能诱导烟气向火源下游蔓延，减弱上游烟气继续蔓延的趋势。

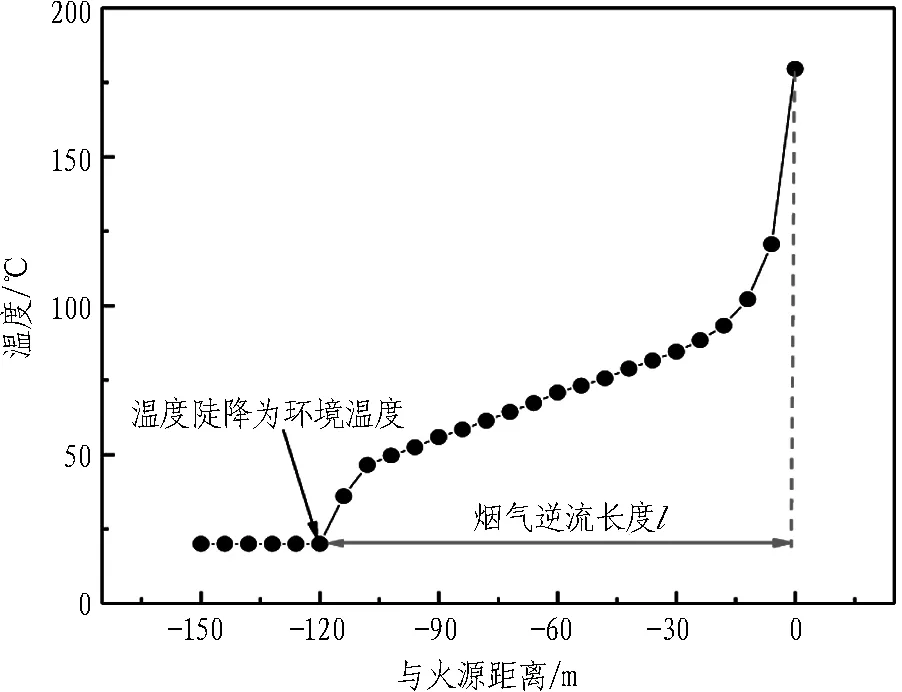
图4 顶板下方烟气温度纵向分布图

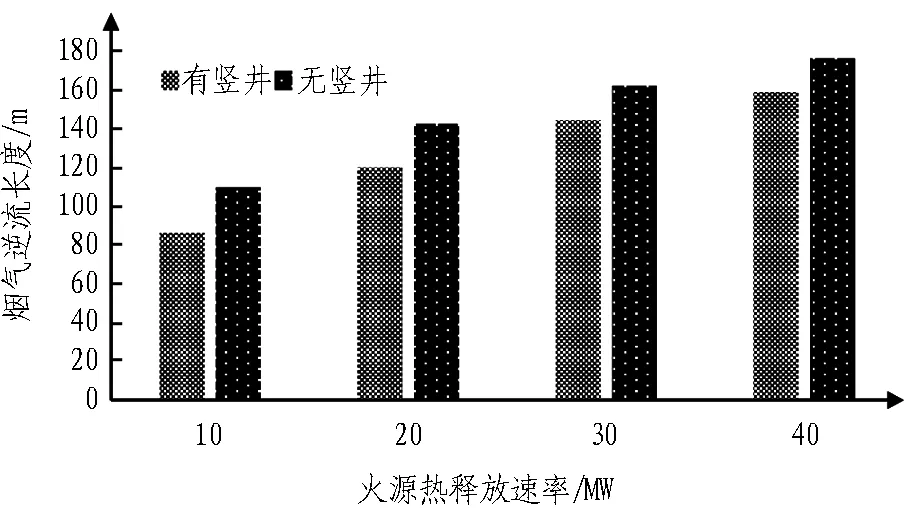
图5 不同火源热释放速率下有无竖井时烟气逆流长度

Fig. 5 Smoke back-laying flow length under different HRRs with and without vertical shaft

3.2 火源热释放速率Q的影响

在纵向风速分别为1.5、2.0 m/s，竖井与火源间距为50 m的情况下，对不同火源热释放速率对上游烟气逆流长度的影响进行研究，模拟结果见图6。随着火源热释放速率的增加，烟气逆流长度逐步增大，但当火源热释放速率超过0.15时，烟气逆流长度变化表现的相对独立，基本不受其影响。火源热释放速率增大使烟气所受热驱动力不断增强，因此烟气逆流长度变大；但由于隧道空间的限制，当火源热释放速率超过一定值时，火羽流上升空间较小甚至触顶，本可充分发展形成的浮力羽流区受到一定限制，因此，受火源热释放速率作用的热驱动力增长也受到抑制，因此，烟气逆流长度增长减缓。

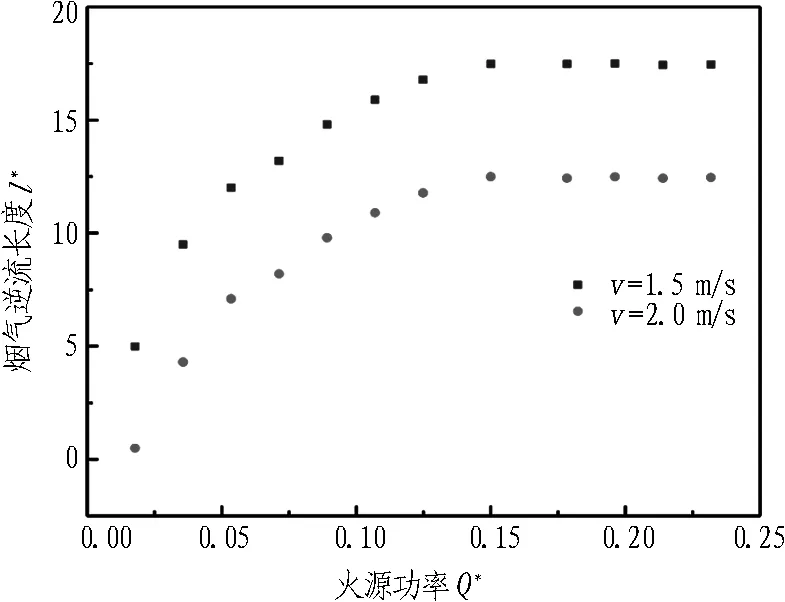
图6 不同火源热释放速率时的烟气逆流长度

3.3 纵向风速v的影响

在火源热释放速率分别为10 MW和20 MW、竖井与火源间距为50 m的情况下，研究竖井排烟模式中火源上游纵向通风对烟气逆流的影响，模拟结果如图7所示。烟气逆流长度随火源上游送风速度增大而逐步减小，因此，纵向送风可有效控制隧道上游烟气逆流。

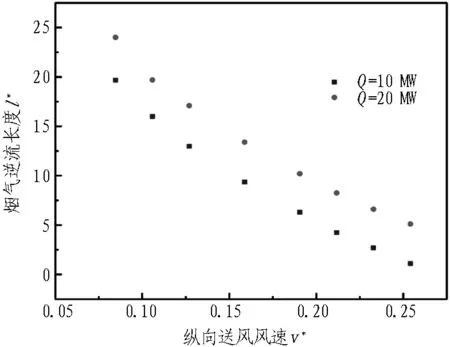
图7 不同纵向送风条件下的烟气逆流长度

Fig. 7 Smoke back-laying flow length under different longitudinal ventilation velocities

3.4 竖井与火源间距d的影响

在火源热释放速率分别为10 MW和20 MW、纵向风速为1.5 m/s的情况下，研究竖井与火源距离对烟气逆流长度的影响，模拟结果见图8。烟气逆流长度随着间距d的增加而增加，但变化幅度逐步减小，当竖井与火源距离超过一定值时，烟气逆流长度趋于稳定，间距d对烟气逆流长度l的影响趋于消失。因为随着竖井与火源距离d的增加，烟气到达竖井时温度逐渐减小，竖井与外界温差降低，烟囱效应减弱，竖井对上游烟气蔓延的抑制作用减弱，因此，间距d越大烟气逆流长度相对越长。当d较大时(d*>13.2)，竖井与火源间距对隧道内火灾影响趋于消失，烟气逆流长度几乎不再随着间距的增加而出现变化。此时，相比较于隧道纵向送风、火源热释放速率等其他影响因素，竖井对火源上游烟气逆流几乎没有影响。

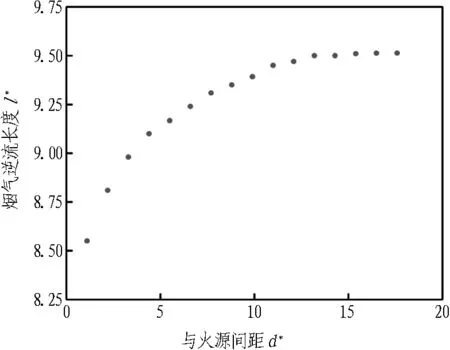
(a) Q=10 MW时

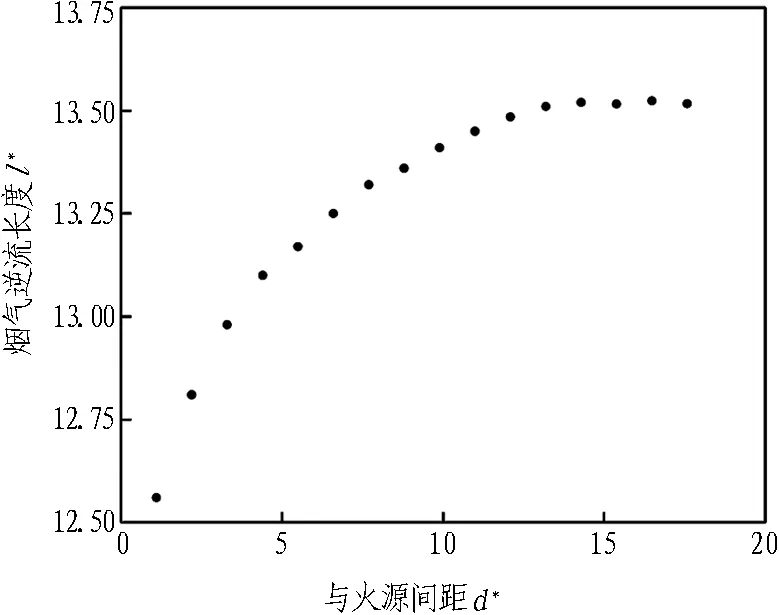
(b) Q=20 MW时

Fig. 8 Smoke back-laying flow length under different distances between shaft and fire source

3.5 竖井高度h的影响

火源热释放速率分别为10 MW和20 MW、纵向风速为1.5 m/s、竖井与火源间距为50 m的情况下，研究竖井高度对烟气逆流长度的影响，模拟结果如图9所示。在其他影响因素不变的情况下，竖井隧道火源上游烟气逆流长度并未随着火源下游竖井高度的变化而发生明显变化。这是因为烟气进入竖井的驱动力主要是烟气的动压和热压。在竖井与火源的距离、竖井宽度等因素一定时，烟气的动压一定，在纵向风的驱动作用下，竖井高度变化对并不能对隧道烟气热压产生较大改变，即东湖隧道竖井大风口尺寸下，火源下游竖井高度对上游烟气的逆流基本无影响。

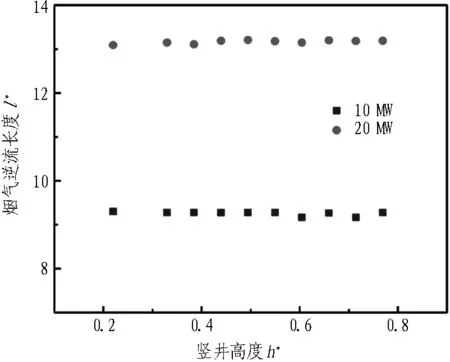
图9 不同竖井高度条件下的烟气逆流长度

3.6 竖井宽度w的影响

火源热释放速率分别为10 MW和20 MW、纵向风速为1.5 m/s、竖井与火源间距为50 m情况下，研究竖井宽度对烟气逆流的影响，模拟结果如图10所示。在其他因素不变的情况下，火源上游烟气逆流长度随竖井宽度变宽而逐渐变小，但变化趋势明显减少。这是因为在隧道纵向风和烟气自身惯性力作用下，当竖井宽度较小时，受烟囱效应影响，大量烟气经竖井排出；当竖井宽度较宽时烟气受自身水平惯性力影响较大，减弱了烟囱效应对隧道烟气蔓延的影响。

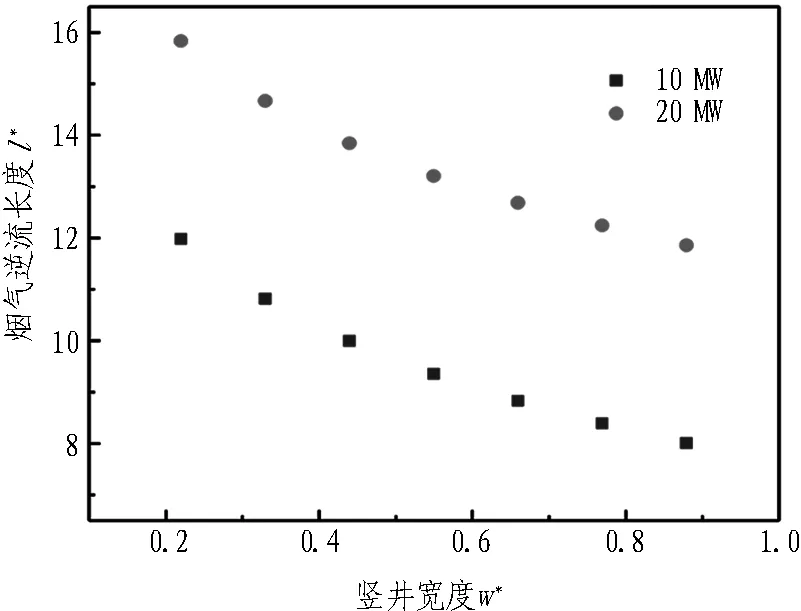
图10 不同竖井宽度时烟气逆流长度

3.7 量纲公式的确定

如图11所示，对数据进行分析，对各影响因素取对数，分别以lnQ*、lnv*、lnd*、lnw*为横坐标，发现l*与5.73 lnQ*、-17.316 lnv*、0.381 lnd*、-2.71 lnw*成线性关系，即l*与5.73 lnQ*、5.73 ln(v*)-3、5.73 lnd*1/15、5.73 lnw*-0.47成线性关系。故l*与lnQ*、ln(v*)-3、lnd*1/15、lnw*-0.47成线性关系，则l*与其四者之和也成线性关系，式(8)可化简为

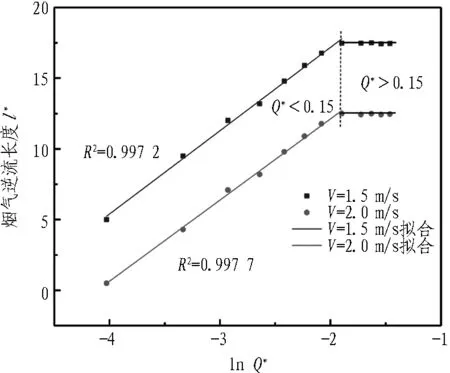
(a) 不同火源功率Q

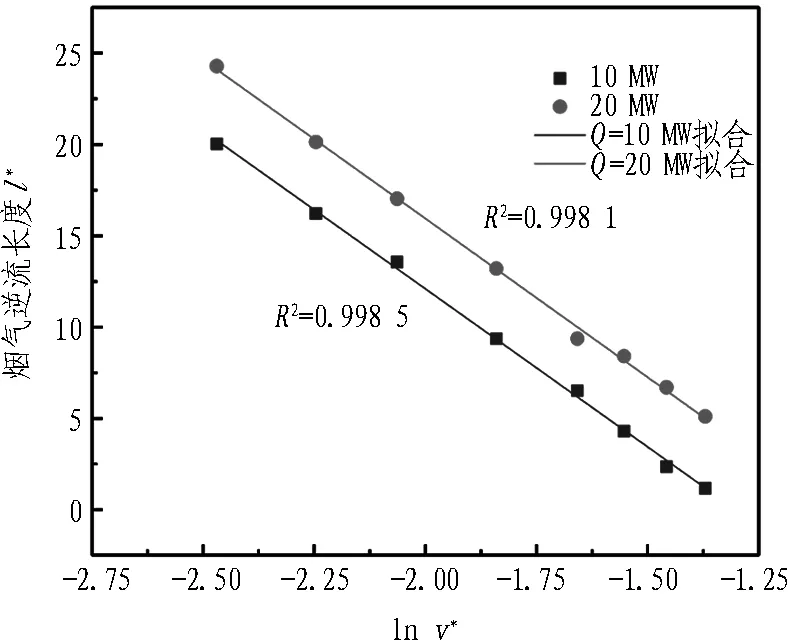
(b) 不同纵向送风风速v

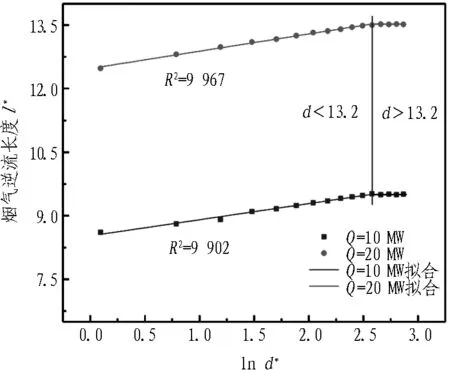
(c) 不同竖井与火源间距d

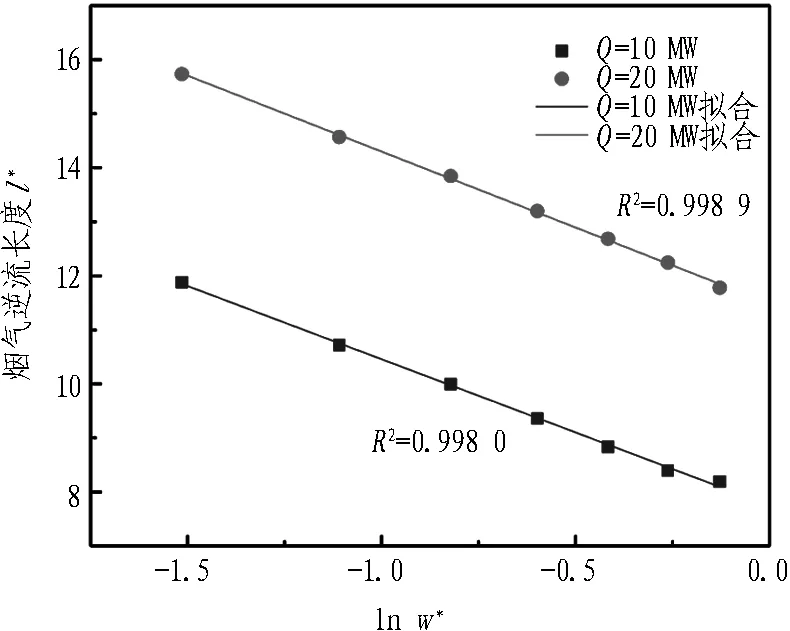
(d)不同竖井宽度w

l*=f(lnQ*+lnv*-3+lnd*1/15+lnw*-0.47)=

f[ln(Q*d*1/15v*-3w*-0.47)]=

f(Q*d*1/15v*-3w*-0.47)。

(10)

根据式(10)将Q*v*-3d*1/15w*-0.47与数值模拟值所得的l*绘于图12。

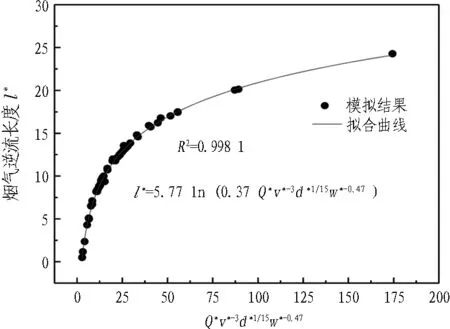
图12 烟气逆流长度数值模拟结果

由图12可得烟气逆流长度数值模拟结果均在拟合曲线附近波动，其相关系数为0.991 1，表明量纲分析和数值模拟的结果是正确可靠的，烟气逆流长度计算模型具有较高的预测精度。在式(10)基础上进一步得到

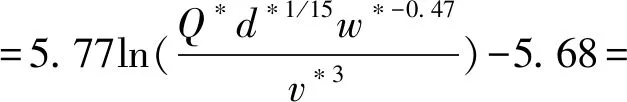
(11)

式中：Q*超过0.15时均取0.15；d*超过13.2时均取 13.2。

3.8 模型对比

在竖井与火源间距为50 m、竖井高度为6 m、竖井宽度为5 m时，仅改变火源热释放率和纵向送风速度，将式(11)预测结果与文献[3,5,18]的计算模型进行比较，以确定式(11)的可靠性。图13(a)中隧道纵向送风速率为1.5 m/s，图13(b)中火源热释放速率为10 MW，与文献[3，5，18]的计算模型相比，式(11)的计算结果偏低。这是因为竖井具有烟囱效应，排出一部分烟气，且竖井一定程度上抑制了烟气向火源上游蔓延，使得烟气逆流长度减小。

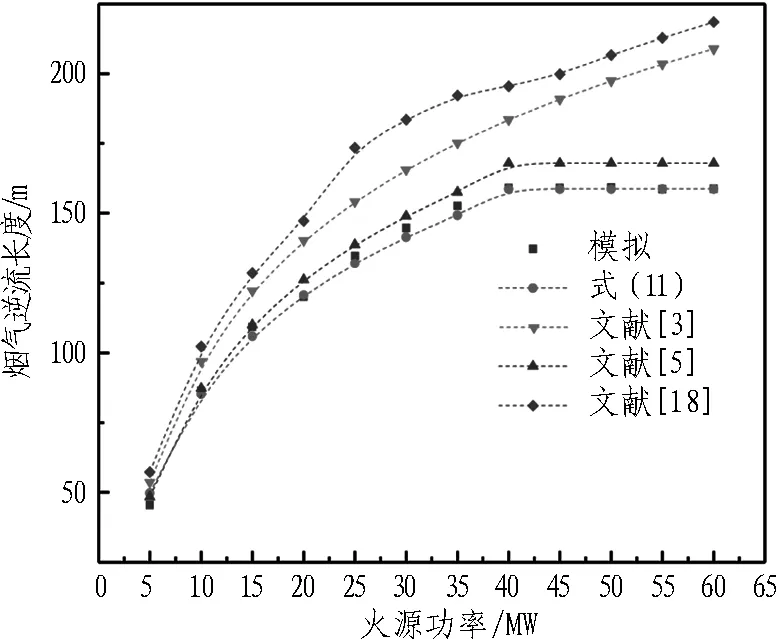
(a) 不同的火源功率 (b) 不同的纵向送风风速

图13计算模型与公式对比

Fig. 13 Comparison between calculation models and formula

4 结论与讨论

采用量纲分析及数值模拟，研究了纵向风作用下竖井排烟时火源热释放速率、纵向风速、竖井与火源距离、竖井宽度和高度等因素对上游烟气蔓延的影响，得到如下结论：

1)竖井排烟对上游烟气蔓延具有抑制作用，上游烟气逆流长度随火源热释放速率Q增长而增大，但当Q*超过0.15时，烟气逆流长度基本不随火源热释放速率变化而变化；竖井与火源距离d的影响与火源热释放速率Q类似，当d*超过13.2时，烟气逆流长度趋于稳定。

2)上游烟气逆流长度与隧道纵向送风v成负相关；竖井宽度的对烟气逆流的影响与隧道纵向送风v类似，火源上游烟气逆流长度随竖井宽度变宽而逐渐变小，但变化范围明显减小。

3)东湖隧道竖井大风口尺寸下，竖井高度的变化对火源上游烟气的逆流并未产生明显影响。

本文明确了竖井排烟时，纵向送风隧道上游烟气逆流与火源热释放速率、竖井与火源距离、竖井宽度等多个量纲之间的关系，并可更好地表征用隧道横断面参数的水力直径替代隧道高度，建立了竖井排烟隧道内火源上游烟气逆流长度预测模型。竖井隧道中，存在竖井长度变化的复杂性和由此带来的无规律性变化，甚至多个竖井的情况，尚未考虑这些因素对上游烟气逆流的影响，可在后续研究中深入展开。