量化私募行业发展趋势的组合预测研究
姚宇航 辜浩诚 龙亚标 余晓銮

[摘 要]文章首先从私募证券基金角度出发,分析和预测了量化投资行业未来的发展趋势;针对存在突破点的机构数量时间序列,在传统的ARMA(1,1)模型基础上,引入了干预分析模型,分析得出对时间序列的拟合效果较好。其次建立了线性回归方程研究机构数量和沪深300的关系,研究得出模型的拟合程度较高。最后为了进一步提高预测模型对时间序列的拟合效果以及预测精度,文章将不同模型的预测精度作为预测值的诱导值,建立了基于IOWA算子的组合预测的模型。
[关键词]量化投资;ARMA模型;线性回归;组合预测
[DOI]10.13939/j.cnki.zgsc.2019.07.049
1 引 言
随着证券市场的复杂程度日益提升,传统投资面临较大挑战,因此越来越多的专业机构,如私募基金公司开始关注量化投资。在我国,量化投资虽然起步较晚,但随着近几年我国随着金融科技产业的蓬勃发展,我国的量化投资行业也进入了一个相对高速的发展时期。自2010年股指期货推出以后,越来越多的海外量化基金经理开始回归国内私募基金市场,越来越多的私募基金开始推出了各自的量化产品。
2 ARMA干预分析模型
文章主要数据为私募证券基金管理人数和沪深300指数的当天平均价格,模型中分别用yt,Pt来表示。
ARMA 模型是研究平稳随机过程有理谱的典型方法,常用于分析长期的时间序列。时间序列yt满足:
文章采用ARMA(1,1)模型作为机构数量的预测模型。由于STATA相当于对去中心化的变量拟合ARMA模型,根据STATA计算结果可得出ARMA(1,1)模型如下:
其中,Δyt表示对机构数量的一阶差分。模型的p值为0.0000,在5%的显著水平下,通过了检验。
将干预影响后的机构数量实际值减去干预影响的预测值,结合干预影响前的机构数量实际值,即为消除了干预影响的机构数量的净化序列。对净化序列建立拟合模型,仍采取ARMA(1,1)进行擬合,结果如下:
模型的p值为0.0000,在5%的显著水平下,通过了检验。
最后用Xt可以表示总干预分析模型,结合干预影响值的模型和机构数量的净化序列的ARMA(1,1)模型,可以组建得到总的ARMA干预分析模型如下:
根据总的ARMA干预分析模型,计算机构数量预测值,并与机构数量的实际值进行对比,结果如下。
模型的拟合效果较好,除了在突破点存在偏差,在时间序列的后期拟合程度较高。
3 线性回归模型
文章采用沪深300指数当天的平均价格作为代理指标,用Pt来表示。沪深300指数是反映沪深两个市场整体走势的“晴雨表”,成分股为市场中市场代表性好,流动性高的主流投资股票,能够反映市场主流投资的收益情况。
因为机构数量在2016年7月存在着突变点,因此引入虚拟变量来衡量外部干预这定性数据,以此修正模型,用Dt来表示。在线性回归模型中,依然对机构数量进行对数处理,但不进行一阶差分处理。
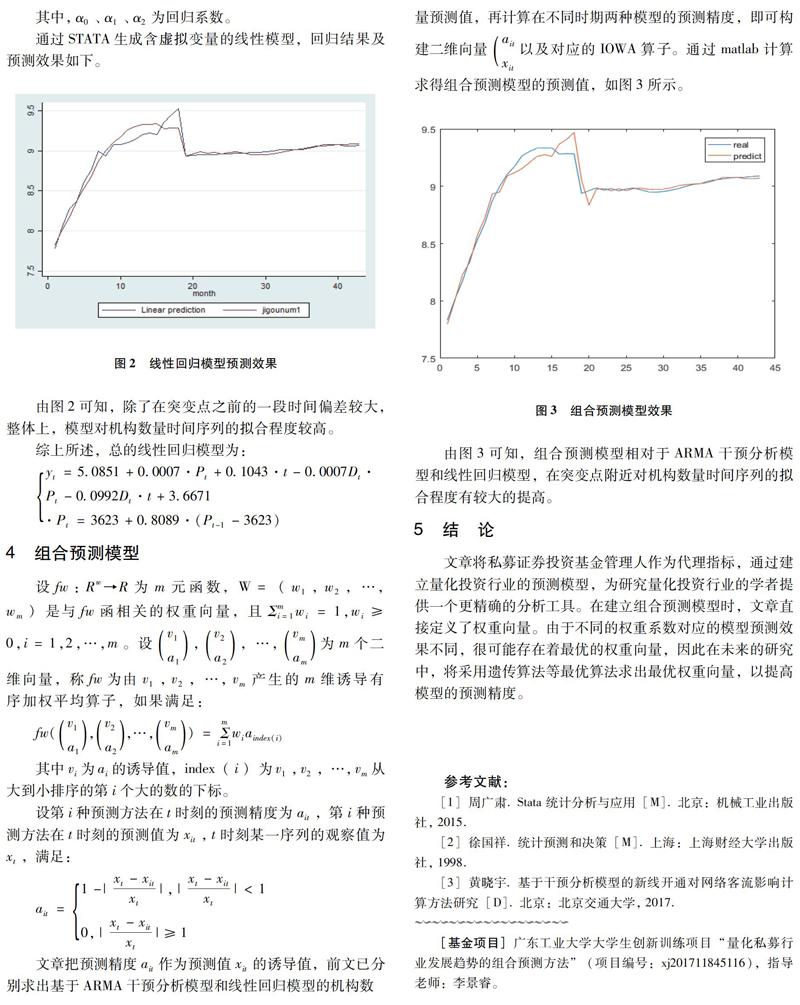
通过STATA生成含虚拟变量的线性模型,回归结果及预测效果如下。
除了在突变点之前的一段时间偏差较大,整体上,模型对机构数量时间序列的拟合程度较高。
综上所述,总的线性回归模型为:
4 组合预测模型
文章把预测精度ait作为预测值xit的诱导值,前文已分别求出基于ARMA干预分析模型和线性回归模型的机构数量预测值,再计算在不同时期两种模型的预测精度,即可构建二维向量aitxit以及对应的IOWA算子。通过matlab计算求得组合预测模型的预测值。
组合预测模型相对于ARMA干预分析模型和线性回归模型,在突变点附近对机构数量时间序列的拟合程度有较大的提高。
5 结 论
文章将私募证券投资基金管理人作为代理指标,通过建立量化投资行业的预测模型,为研究量化投资行业的学者提供一个更精确的分析工具。在建立组合预测模型时,文章直接定义了权重向量。由于不同的权重系数对应的模型预测效果不同,很可能存在着最优的权重向量,因此在未来的研究中,将采用遗传算法等最优算法求出最优权重向量,以提高模型的预测精度。
参考文献:
[1]周广肃. Stata 统计分析与应用[M]. 北京:机械工业出版社, 2015.
[2]徐国祥. 统计预测和决策[M]. 上海:上海财经大学出版社, 1998.
[3]黄晓宇. 基于干预分析模型的新线开通对网络客流影响计算方法研究[D]. 北京:北京交通大学, 2017.

