压力分散型锚索加固高边坡机理研究——以灵石石膏山水库左坝肩高边坡为例
连幼奇
(山西省晋中市水利建筑工程总公司,山西 晋中 030600)
锚固是一种常用的支护措施,在基坑[1]、地下洞室[2]、边坡[3]加固中应用广泛。王光勇等[4]结合数值模拟和相似试验,对岩体裂隙倾角和长度对锚固洞室损伤和变形进行了研究,随着裂隙倾角增大,损伤区域面积先增大后减小。何栋梁等[5]采用颗粒流数值模拟分析锚固节理破坏模式,认为锚固角度较大时,锚固与节理接触面会发生明显的核破坏,随着锚固角度的增大,峰值剪切应力先增大后减小。兰奕文等[6]针对煤巷变形控制难,综合多种方法,研究了巷道变形特征,提出顶板全锚索控制系统。陈家昊等[7]研究了密实型索体预应力锚索的锚固机理,结果表明:荷载作用挤压注浆体时最大剪应力位于锚固段最末端,其数值随着荷载的增加而增大。文章结合灵石石膏山水库左坝肩高边坡工程特点,研究压力分散型锚杆加固高边坡的机理。
1 工程概况
石膏山水库位于晋中市灵石县,属于仁义河流域。坝型采用混凝土拱坝,最大坝高68 m,坝顶长度169 m,属小型水库。左坝肩坝顶上为开挖边坡,坡高60.0 m,坡度70°—80°。边坡后缘发育多条拉张裂隙,岩体极为破碎,边坡稳定性较差。
2 压力分散型锚索加固机理分析
根据受力状态,锚索可分为压力型和拉力型。一般情况下,压力型锚索锚固段刚束与承载体直接连接,压力型锚索荷载通过刚束传递将直接作用在承载体上,压力型锚索荷载传递可以看做是从下向上传递。压力型锚索结果见图1。影响压力型锚索的主要因素是锚固段浆液的强度。当压力型锚索承载力达到一定程度时,内部承载体将发生变形破坏,一般多发生于承载体上部应力集中段,压力型锚索应力分布见图2。应力集中位于承载体,向孔口方向应力逐渐降低,承载体位于强度较高的岩体中时,压力型锚索承载力将大于拉力型锚索,因此,在强度较高的岩体加固工程中,压力型锚索较为适用。

图1 压力型锚索
压力型锚索应力分布较为集中,这对其承载力有较大的影响。采用荷载分散型锚索可分散压力型锚索锚固段的应力,避免应力集中造成承载体局部破坏,从而造成锚索失效。压力分散型锚索结构见图3。锚固段应力分布情况见图4,从图中可知锚固段应力分布较为均匀,与图2 相比,避免了荷载集中造成锚索失效现象的出现,大大提高了锚固力。
3 石膏山水库左坝肩高边坡治理效果
3.1 边坡地质情况
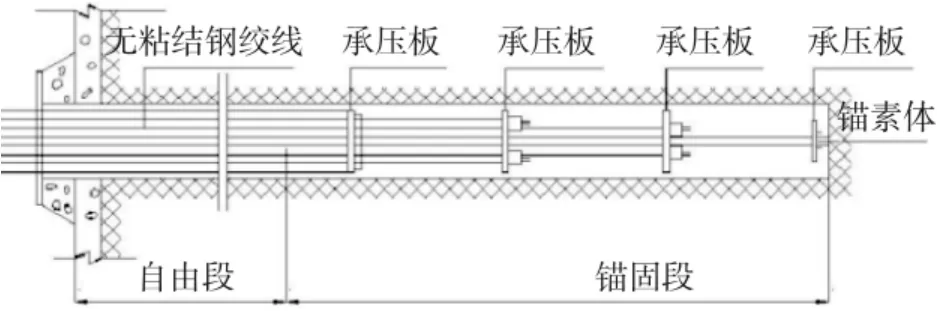
图3 压力分散型锚索结构
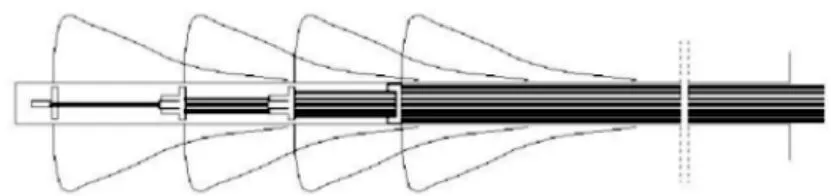
图4 压力分散型锚索锚固段应力分布
大坝左岸为凸出山梁,高程约为1 160 m,坝顶以上部位山脊宽度在70.0 m 左右。左坝肩开挖后,最大坡高为60.0 m,边坡岩体主要为花岗岩、片麻岩,边坡岩体结构较为破碎,承载力较低。根据室内力学试验结果,石膏山组第二岩组(ATs-2)岩石单轴饱和抗压强度49.1~97.0 MPa,饱和变形模量(3.30 ~6.02)×104MPa,泊松比0.14~0.22,饱和抗剪断强度C 为0.67~4.9 MPa,内摩擦角为43.9~47.5°。
由于左坝肩边坡开挖后形成坡度较大的人工边坡,边坡岩体内部存在强度较低的破碎片麻岩等,提出采用压力分散型锚索进行锚固处理。
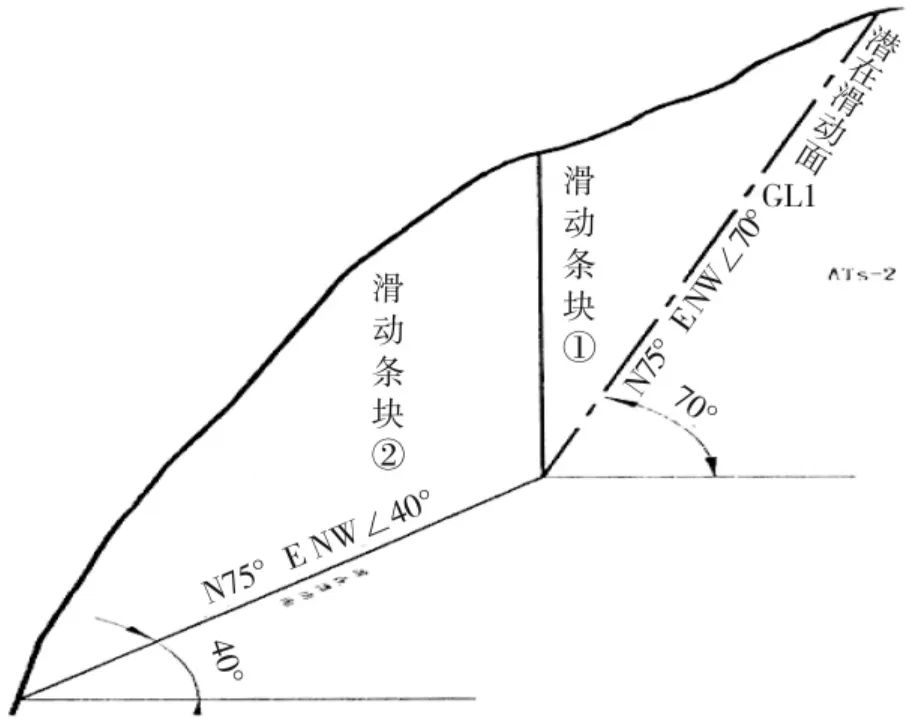
图5 边坡概况
3.2 压力分散型锚索设计分析
采用条分法确定下滑力,计算公式如下,计算参数见表1。
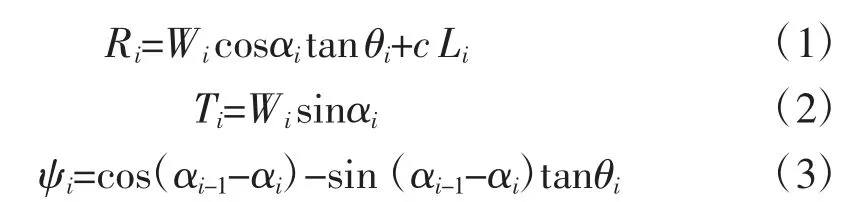
式中:Wi——第i 块滑动条块侧面的推力传递系数;
Ri——第i 块滑动条块侧面的推力传递系数;
Ti——第i 块滑动条块侧面的推力传递系数;
ψi——第i 块滑动条块侧面的推力传递系数;
C——滑动带岩的凝聚力,kPa;
θ——滑动带岩的内摩擦角,°;
αi——第i 块滑动条块滑动面的倾斜角,°;
Li——第i 块滑动条块滑动面的长度,m。
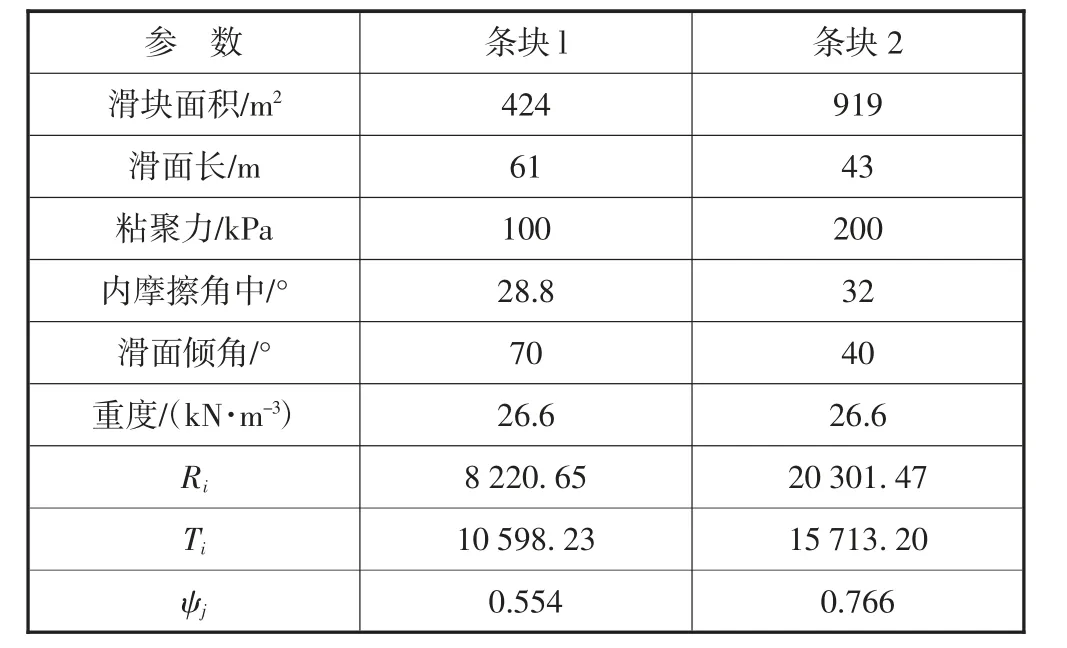
表1 计算参数
通过计算下滑力F 为3 500 kN,则锚固力采用下式计算:
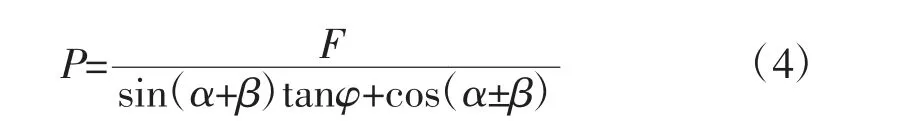
式中:P——设计锚固力;
φ——滑面内摩擦角,18.5°;
a——锚索、滑面相交处滑面倾角(40°、70°);
β——锚固角,15°。
预应力锚索是群锚机制,根据张拉试验,锚索间距小于1.2 m 时,会影响锚孔周围岩土,因此,设计锚索间排距为3 m。根据剖面工程情况,最大开挖断面坡长41 m,可布14 排锚索,则单孔锚索设计锚固力为:
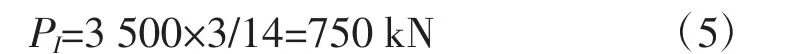
根据计算结果,设计锚固力为750 kN。锚索钢绞线采用中φ15.2 mm,抗拉强度1 860 MPa,每根极限张拉荷载为259 kN,每孔锚索根数计算如下:

式中:Fs——安全系数,取1.8;
Pu——钢材极限张拉荷载。
通过计算,n=5.21,设计采用6 根。锚固段长度采用下式计算:

式中:Fs2——抗拔安全系数,取2.5;
dh——钻孔直径,取0.13 m;
τ——毛孔壁对砂浆极限剪应力,取1 200 KPa。
计算锚固段长度为3.83 m,结合破碎带的局部变化,为了保证锚索的可靠性,在一定程度上对锚固段进行加长,最终确定锚固段长度为9.0 m,自由段平均长度约29 m。
3.3 压力分散型锚索加固效果分析
数值模拟采用FLAC3D 软件,该软件由Itasca 公司开发,在岩土工程数值模拟分析中较为常用。FLAC软件最明显的特征是节点位移是连续的,对岩土体非线性变形的分析结果较为可靠。
根据边坡地质情况建立FLAC 数值模拟模型,分析支护前后边坡的稳定性情况及位移量。数值模拟模型见图6。从上至下依次布置A~N,共14 个监测点,监测边坡的变形情况。数值模拟模拟天然工况下的边坡稳定性情况,模型底部及两侧为固定边界,边坡部位为自由边界条件,在建模过程中,划分网格大小为0.5 m,计算控制方程采用摩尔—库伦模型。
图6 数值模拟模型
边坡开挖后位移云图见图7,从图中可知未采取治理措施,边坡位移较大,最大值可达30.6 cm,边坡剪应力主要集中于后缘拉张裂隙与坡脚处,虽然治理前边坡并未产生贯通的破坏面发生整体破坏,但局部的应力集中表明坡体内部存在潜在的破坏面,在后期的降水、重力、地震等因素综合作用下,岩体极易沿着潜在破坏面的滑动或者倾倒破坏,从而威胁到坡体下方构筑体的正常使用。
封填后缘拉张裂隙并采用锚索支护后的位移云图见图8,从图中可知,加固后边坡变形量明显减小,最大变形量为4.23 cm 这表明采用压力分散型锚索可以较好地控制该边坡的变形。

图7 开挖后位移云图

图8 加固后位移云图
加固前后各监测点的位移变形监测量见表1。从表1 可知,加固前后最大位移均发生在坡顶监测点A处,加固前各监测点变形量在16.5~30.6 cm 之间,加固后各监测点位移范围在3.08~4.23 cm 之间,加固后坡体变形处于相对协调的状态,避免了位移变形不协调从而诱发斜坡破坏的现象。
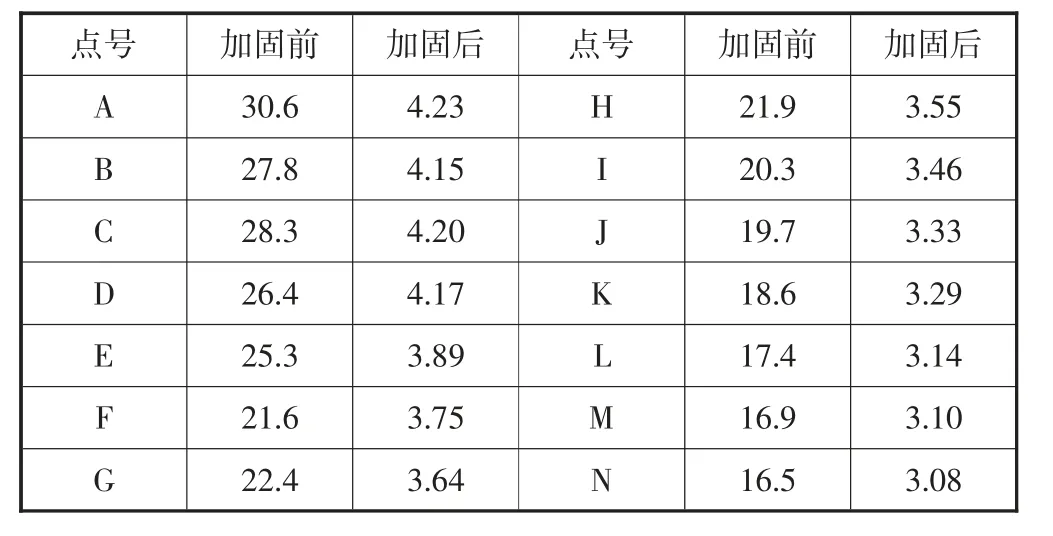
表1 加固前后位移量对比 单位:cm
4 结论
锚固在边坡加固中较为常用,采用压力分散型锚索可在相同的地质条件下提供更大的锚固力,从而满足边坡加固要求。结合石膏山水库高边坡,通过计算确定锚索加固方案,通过数值模拟对比,加固后边坡位移明显减少,表明锚索具备较好的控制边坡位移的效果,且加固后各监测点的位移差值也明显降低,表明边坡变形属于协调状态,可避免变形量差值较大造成边坡局部应力集中现象的出现。

