气液比对压裂返排液旋流除砂器性能的影响

刘培坤 王华健 赵振江 李伦操 肖小龙 张 华 刘 冰

1. 山东科技大学机械电子工程学院 2. 油田采出水处理及环境污染企业重点实验室

0 引言

为了达到排放和回注的有关要求，压裂返排液在化学处理之前为避免高速流动的固体颗粒对管道和设备造成磨损及刺漏，首先需要将固体颗粒物清除[1-2]。水力旋流器由于分离精度高、占地面积小、操作简单而被应用于压裂返排液的旋流除砂[3-4]。然而由于压裂返排液成分复杂[5-7]、黏度大，并且携带有气体[8]，增加了内流场的复杂性，从而抑制了旋流器性能的充分发挥，导致其应用范围受到限制。

褚良银等[9-10]通过壁面充气的方式研究了水力旋流器的内流场、离心力强度等，为我国充气水力旋流器的研究奠定了基础。蒋明虎等[11]、赵立新等[12-13]在研究双锥液—液水力旋流器的过程中发现注气方式、结构参数和操作参数均要对水力旋流器的分离性能产生影响，然而其研究重点在液—液分离，并未研究气体对固—液分离的影响；徐保蕊等[14]、蒋明虎等[15]通过对内锥式三相旋流器进行模拟实验研究，发现随着气液比升高能够在一定程度上提高固体的分离效率，但是却未能定量研究气液比对内流场的影响。Bokotko等[16]对细小颗粒浮选方法及浮选原理进行了研究，Baker等[17]侧重于空气与水在充气水力旋流器中滞留量及滞留时间的研究。近年来，虽有专家研究了壁面充气水力旋流器的气液比对水力旋流器性能的影响[18]，并将充气水力旋流器作为反应容器实现了物料分离[19]，但是这类水力旋流器无论是充气方式还是结构都与目前用于压裂返排液除砂的水力旋流器差别较大。

为了提高水力旋流器的分离性能，以柱段直径为50 mm的水力旋流器为研究对象，利用雷诺应力模型（RSM）＋混合物模型（Mixture）模拟了较大范围气液比（介于0～50%）下水力旋流器的分离性能。由于目前对空气柱的认识尚不明确，首先，对空气的运动轨迹进行研究，揭示了空气柱形成机理，在此基础上确定了空气柱与压力间的相互关系；然后，模拟了不同气液比（GLR）下水力旋流器分离流场（速度、压力）和分离效率，并通过实验对比了底流液封装置下的分离效果；最后，总结了入口GLR对水力旋流器分离性能的影响规律，确定了最佳入口充气范围。所取得的研究成果进一步揭示了水力旋流器的分离机理，可以为水力旋流器的优化设计提供参考。

1 数值模拟与实验

1.1 数值模拟模型

模拟计算及验证性试验采用的模型结构如图1-a所示。为了提高模拟精度，流场域全部采用六面体结构网格，同时为了更好捕捉边界特征以及提高网格划分精度，采用局部加密的方法对壁面及溢流管处进行网格加密，网格划分如图1-b所示。考虑到气液固三相间的压力速度耦合，模拟模型采用多相流Mixture模型，并将RSM模型作为内部湍流模型。其中Mixture模型在水力旋流器三相模拟中的介绍详见本文参考文献[14,20-21]。

此次研究模型参考Zhang等[22]所用模型的具体尺寸（表1）。为了确定入口充气量对水力旋流器的影响，对GLR介于0～50%的内流场及外特性（压降与分离效率）进行了研究，具体物性参数如表1所示。对压裂现场返排液进行采集并通过BT-9300S激光粒度分析仪测出90%的颗粒直径介于5～30 μm，粒度分布如表2所示；利用超级旋转流变仪Kinexus测得混合液黏度为1.3 mPa·s；混合液密度为1 020 kg/m3。

模拟过程中水的入口流量不变并将其作为连续相处理，GLR通过空气体积流量占水与空气总体积流量的比值来控制，并将空气与固体颗粒作为离散相处理。入口处采用速度入口作为边界条件，方向沿入口横截面法线方向，出口处采用压力出口为边界条件，离散相方程采用QUICK差分格式，压力—速度的耦合采用SIMPLE算法，壁面不可渗漏，无滑移条件。

表1 模型参数表

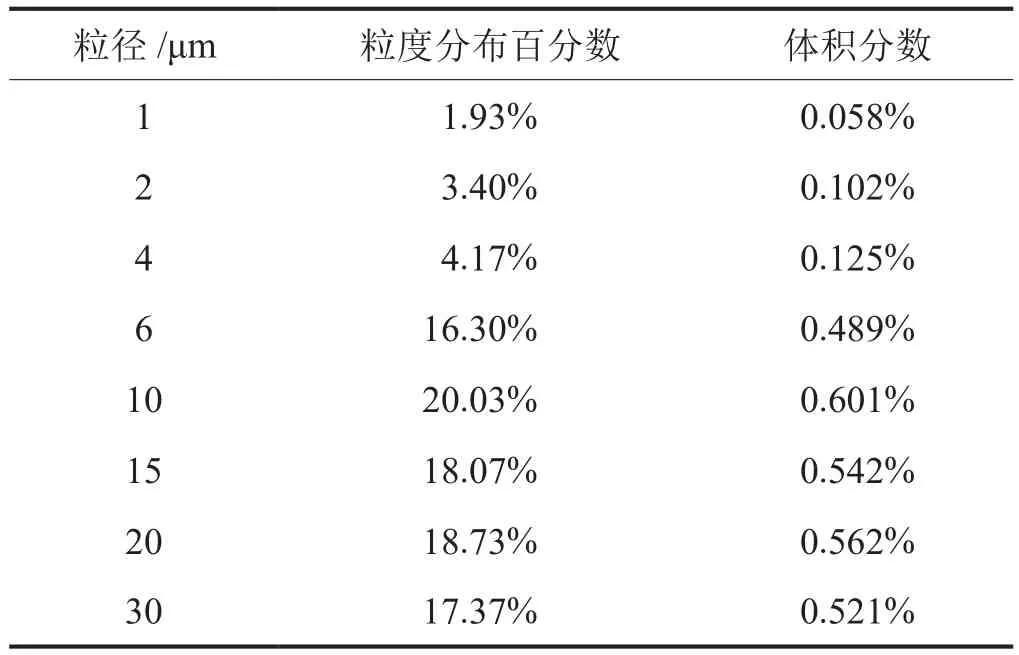
表2 固相颗粒粒度分布统计表

1.2 实验流程

实验流程如图2所示，压裂返排液在储液罐内通过搅拌经螺杆泵增压泵出；利用控制阀控制气体流量，气相及含固相的液体通过静态混合器混合均匀后进入旋流器进行分离。通过入口处与出口处的压力表分别测量压力，并求出溢流压差与底流压差。实验所测得的分离效率为底流口固相质量流率与入口固相质量流率的比值，待接样完成后对样液进行过滤、烘干、称量，进而计算得到分离效率。

1.3 数值模拟模型可靠性

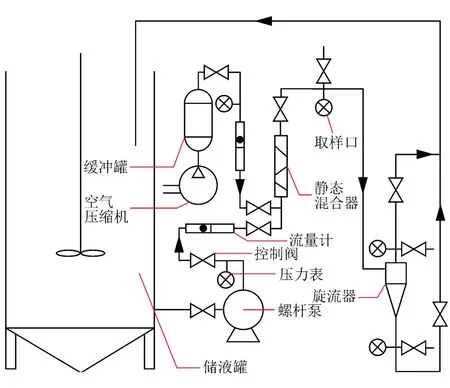
图2 实验流程图

为提高计算精度、减少模拟时间，在数值模拟之前需要对网格数的合理设置进行研究。为此，笔者对网格数为 30×104，35×104，40×104，45×104，50×104的模型分别进行模拟，然后将沿水力旋流器轴向z=36 mm处的轴向速度进行对比，如图3所示，当网格数超过40×104以后，随着网格数逐渐增加，模拟值均较接近，由此，网格数设置在40×104较适宜。然后，将数值模拟和实验测试的不同入口流速下的溢流压差（入口压力与溢流口压力的差值）进行对比，如图4所示，模拟值与实验值较吻合，可见所建立的模拟模型可靠。

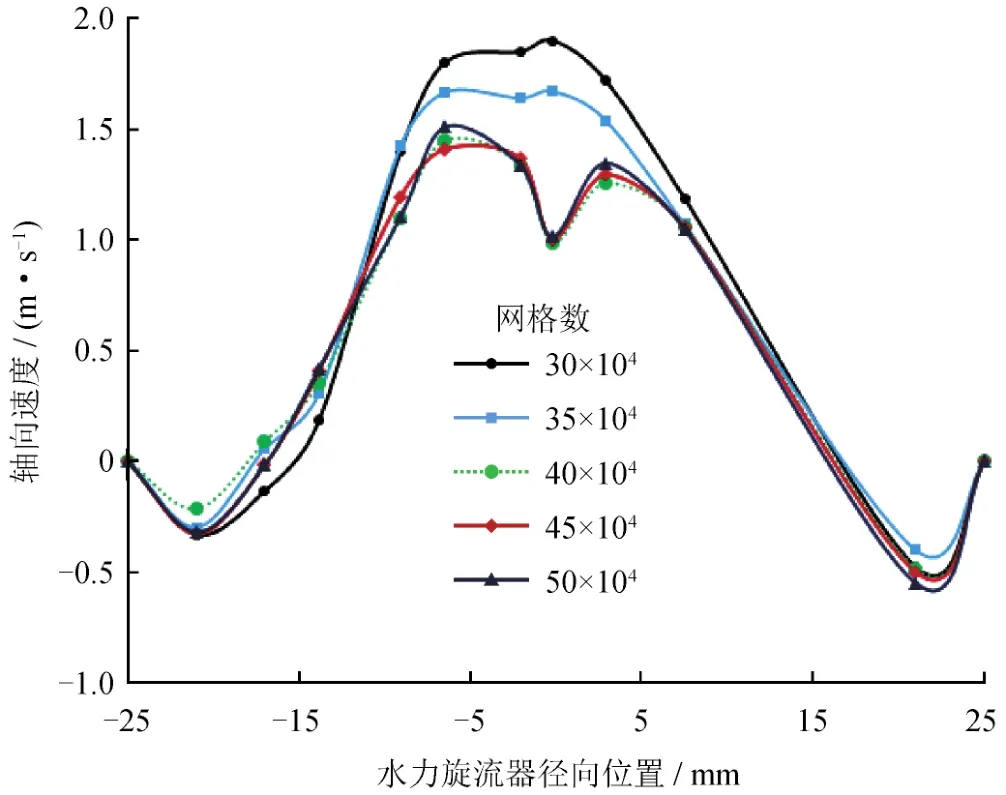
图3 不同网格数下水力旋流器轴向速度模拟结果对比图

2 结果分析

2.1 空气柱直径

空气柱形态决定了内流场的稳定性，其直径是传统水力旋流器一项重要的参数[22]。关于空气柱的形成机理及对水力旋流器性能的影响尚不明确，并且目前尚未对入口充气条件下空气柱的形成过程及稳定状态进行系统的研究。

图4 溢流压差数值模拟与实验测试结果对比图

如图5所示，当GLR等于0时，由于内流场存在负压区，使外界空气通过底流口与溢流口吸入水力旋流器内部，并在轴心处形成空气柱（图5-a）；当GLR＞0时空气柱的形成除来源于前述底流口、溢流口吸入的空气外，还来源于物料中的空气（图5-b～f），这与Neesse和Dueck[23]研究的结果相似，但是，形成水力旋流器中心空气柱的气体主要来自溢流口与底流口，物料中夹带的大部分气体会通过溢流口随着液体排出，只有小部分气体进入空气柱（图6）。

自底流口、溢流口吸入的空气最终都会通过溢流口排出，物料中的小部分气体通过底流口排出。从z由-169.5 mm至36 mm的范围内，空气柱的形成主要来自底流口，同时自溢流口与底流口吸入的空气会在溢流管底部相遇，从而使得空气柱直径在溢流管底部区域突然变大。随着气液比升高，从溢流口吸入的空气增多，并且自溢流口与底流口进入的空气相遇的位置下移（图6）。

如图7所示，在不同GLR下，空气柱直径沿轴向变化的总体趋势相同，但在相同轴向位置处，空气柱直径仍存在一定差异；处于溢流口底部（z=36 mm附近）时空气柱直径突然增大，然后不断减小，空气柱直径最小值出现在锥段中部（z=-70 mm附近），而后不断增大并在底流口处（z=-150 mm附近）剧烈震荡。水力旋流器柱锥交界面附近（z=0 mm附近）是GLR对空气柱直径产生不同影响的转折面，即在该交界面以上，随着气液比升高，空气柱直径不断变大，而在该交界面以下，随着气液比升高，空气柱直径不断减小。

2.2 压力分布

水力旋流器径向压力场的压力梯度直接影响颗粒的分离效果，并且宏观上水力旋流器中能量的损失表现为进出口的压力降，因此需要对水力旋流器进出口的压降开展相关研究[24]。如图8所示，随着GLR升高，壁面压力（径向位置为25 mm）呈现非线性增长的趋势，即压力增幅为先增加后降低，这是因为液体流量为定值，当气液比升高时入口处的压力也相应增加，当GLR过大（GLR＞40%）时，空气使得内流场中能量的损耗变大，因此压力增幅逐渐减小。如图8所示，轴心处（径向位置介于-2.5～2.5 mm）压力随气液比变化的趋势与壁面处相似，在柱段区域，随着气液比升高，负压区范围不断增大，而在锥段区域，随着气液比升高，负压区范围不断减小，这与空气柱直径随气液比变化的趋势也一致（图7），从另一个角度揭示了水力旋流器轴心负压区即为空气柱存在的区域。

图5 内流场空气流体迹线图

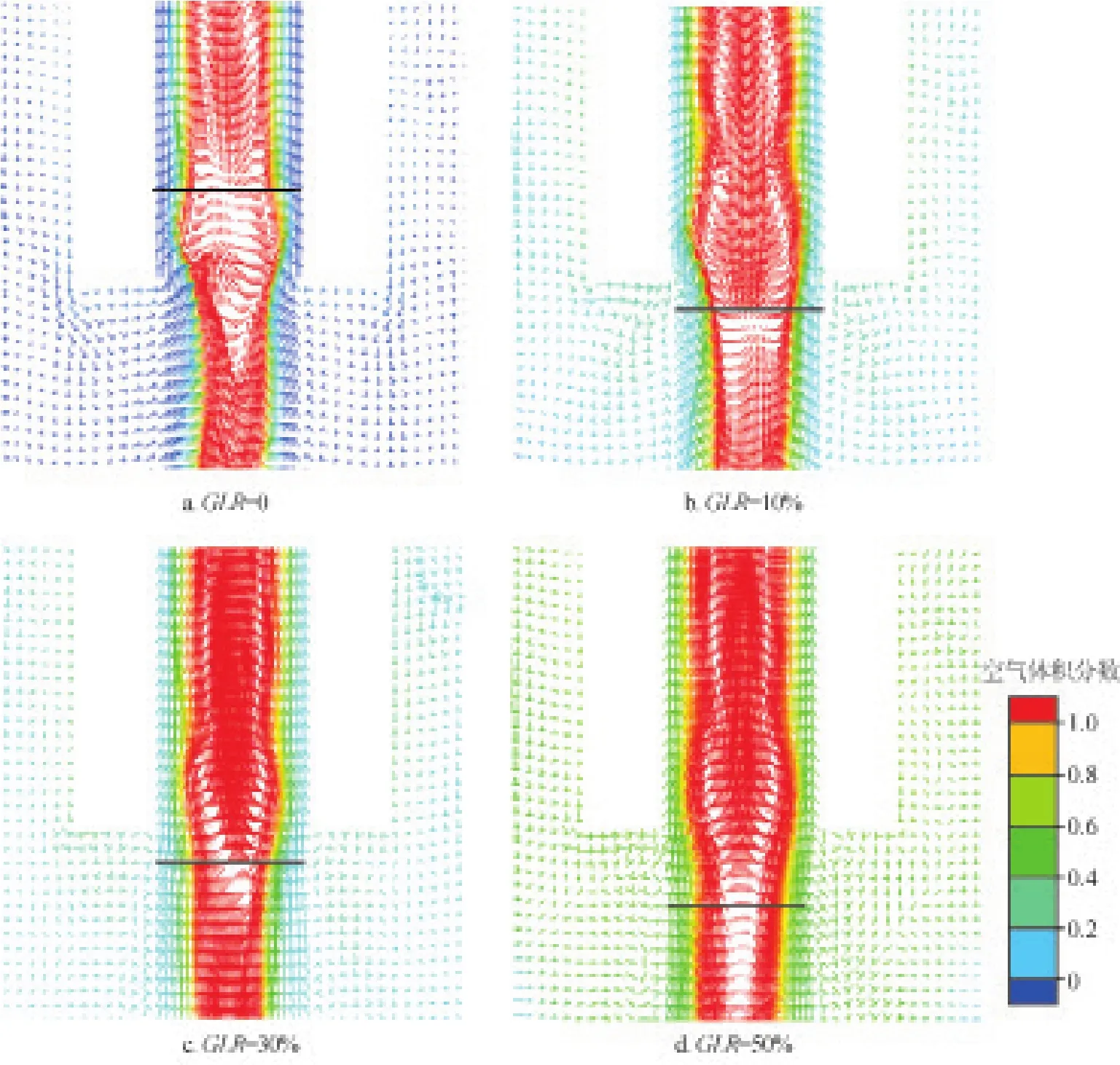
图6 气相运动矢量图

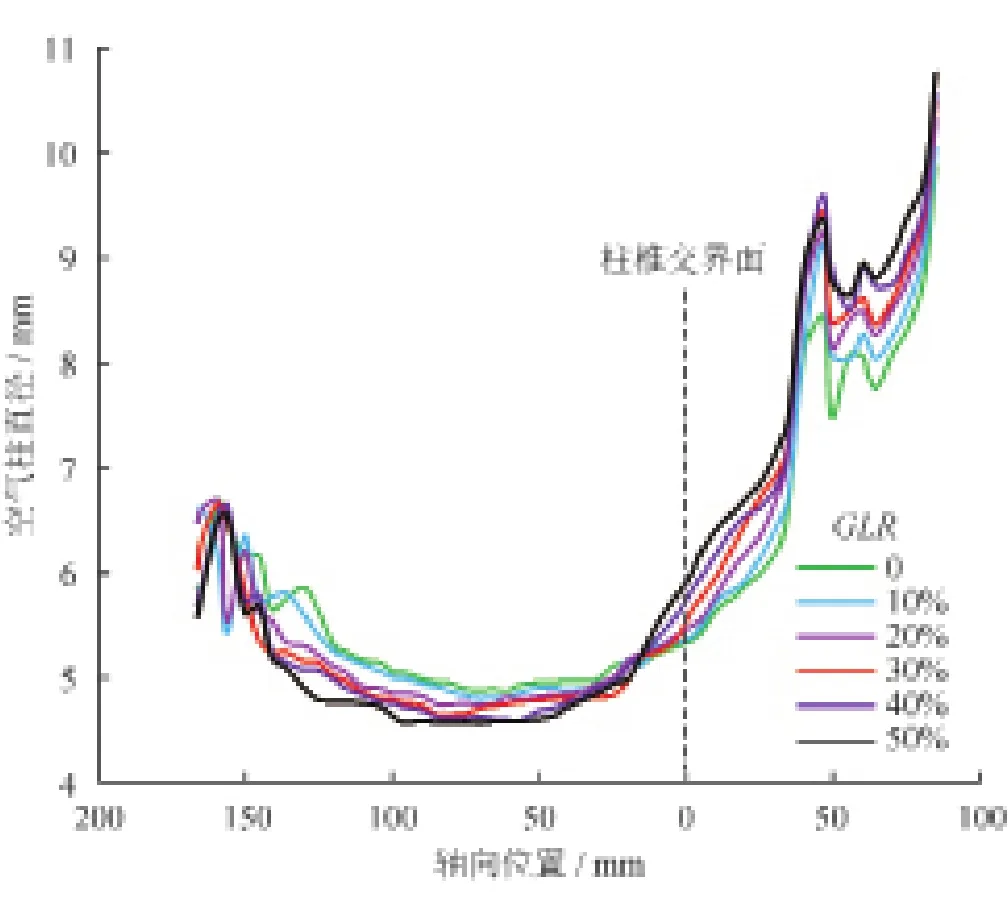
图7 不同气液比下空气柱直径特征曲线图

如图9所示，随着GLR升高，溢流压差与底流压差（入口压力与底流口压力的差值）均逐渐升高，这与褚良银等[25]得出的数据不同，初步认为是由于充气方式及结构不同而引起的，并且溢流压差略小于底流压差，从而使得从底流口吸入的空气流量大于溢流口吸入的空气流量。随着GLR均匀升高，压差呈现非线性增长，这与压力在壁面的分布相似，并且压差约等于壁面处压力的大小。

由实验结果显示，当GLR超过30%以后，底流压差与溢流压差增幅不断减小；当GLR由20%增至30%时，底流压差增幅最大，提高了45.9 kPa，并且溢流压差略小于底流压差。另外，模拟结果与实验结果接近。较高的压差在一定程度上能够提高水力旋流器的分离效率，但也相应增加了内流场的能耗。综合前述分析，认为入口GLR不应超过40%。

2.3 切向速度分布

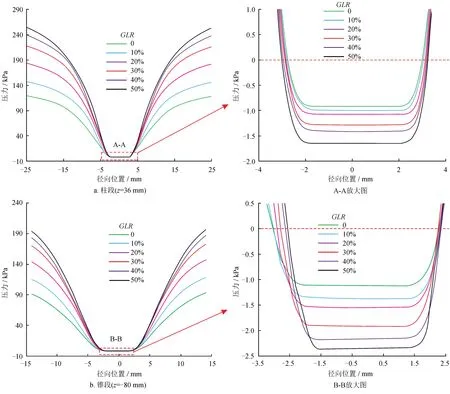
图8 水力旋流器压力分布曲线图

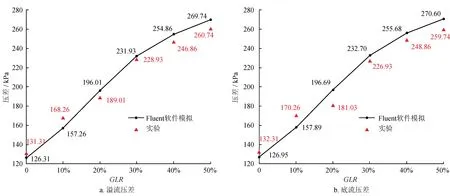
图9 水力旋流器压差与GLR关系曲线图

图10 水力旋流器切向速度分布曲线图

在水力旋流器三维速度场中，切向速度是产生离心惯性力的关键因素。如图10所示，在整个内流场区域，随着气液比升高，切向速度不断地升高，并且柱段切向速度大于锥段切向速度，这是因为气液比升高使得水力旋流器入口处混合流体速度增大，从而增加了整个内流场的速度[26]；当物料在重力的作用下不断下移时，由于内部流场能量损失及物料间的相互作用，锥段区域切向速度减小。GLR为0时，柱段强制涡区（咖啡色矩形区域）切向速度随着旋转半径减小而不断升高；当气液比为10%、20%时切向速度随着旋转半径减小呈现先减小后增大的趋势，这与内流场湍流强度升高有关[22]；当GLR超过20%后，柱段强制涡区切向速度又呈现出不断升高的趋势。

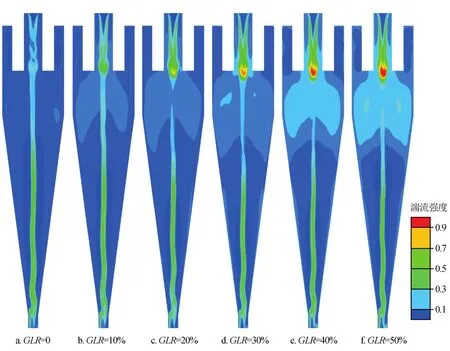
图11 水力旋流器内流场湍流强度云图

湍流强度定义为湍流脉动速度与平均速度的比值，湍流强度的大小会影响到水力旋流器内部错位粒子（未达到预定位置的粒子）的数量，最终影响水力旋流器的性能。如图11所示，随着GLR升高，湍流强度不断升高，整个内流场中湍流强度最高点出现在溢流管底部区域，并且柱段湍流强度高于锥段，这是由于通过底流口与溢流口吸入的空气在此处碰撞而引起的。当GLR大于30%以后，切向速度在柱段强制涡区随着旋转半径减小而不断升高，可见水力旋流器湍流强度并不是决定水力旋流器内部半自由涡区（无外界能量输入给流体并且流体总压头保持恒定的区域）切向速度降低的唯一标准[22]。

水力旋流器切向速度分布呈现出严格的组合涡流场形态，为了进一步研究切向速度，对忽略重力的伯努利方程进行整理，进而得到水力旋流器的组合涡流场通式，即

式中ut表示流体切向速度，m/s；r表示流体的旋转半径，mm；n表示组合涡流场运动指数，无量纲；c表示常数。

基于前述模拟结果（图10-a），假设相邻两点之间流体的运动符合组合涡流场通式，根据式（1）可以求得相邻两点的n值[27]，即

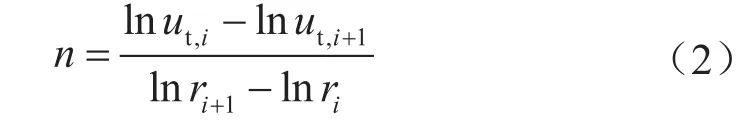
如表3所示，当GLR逐渐升高时，n值迅速减小然后逐渐上升，并且在水力旋流器沿中心至器壁的半自由涡区n值也呈现出先减小后上升的趋势。当GLR为10%、20%时，在径向位置22 mm处n值为负数，并且通过图10咖啡色矩形区域可以看出径向位置处于-20～22 mm的区域内切向速度呈现出下降的趋势，这是由于气液比升高使得湍流强度升高所导致的。当GLR较低时，n较小，甚至为负值，因此不利于内流场中颗粒朝壁面方向的运移，在研究范围内，综合考虑切向速度特征曲线与组合涡流场运动指数，认为入口气液比应高于30%。

表3 水力旋流器z=36 mm处不同径向位置组合涡流场运动指数（n）统计表

2.4 轴向速度分布

如图12所示，随着气液比升高，轴向速度持续升高，尤其表现在柱段旋流区，并且溢流管内蓝色区域面积在不断增加，颜色也在不断加深，说明此处空气吸入量与速度都在增加；随着气液比升高，溢流管管壁区域沿轴向向上的速度在不断增加，从而使得旋流所携带的物料快速通过溢流口排出。轴心处红色柱状区域即为空气柱所在区域，当气液比升高时红色区域长度减小，这也揭示了气液比升高将使得从溢流口与底流口吸入的空气相遇的位置下移。

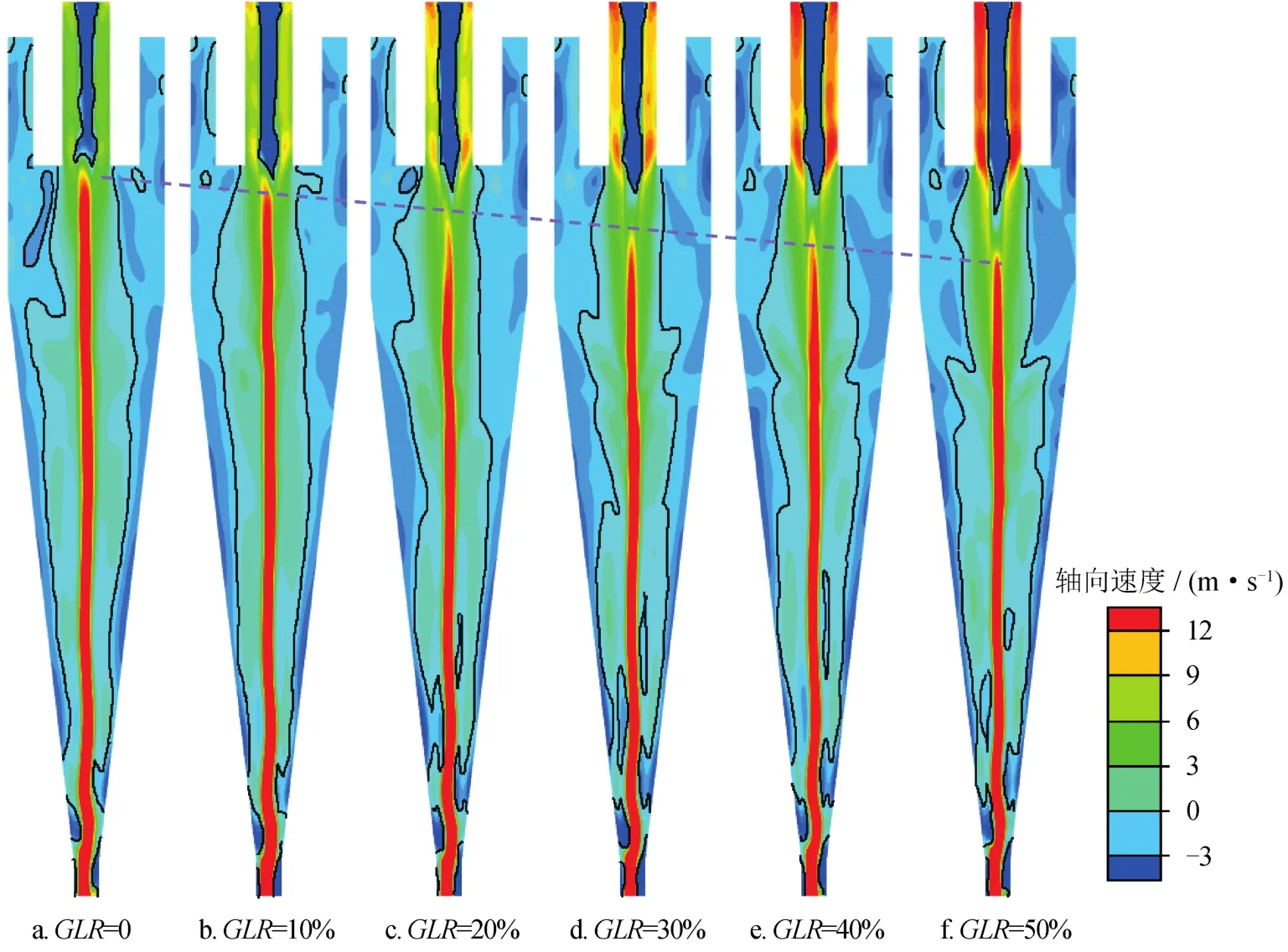
图12 水力旋流器轴向速度云图

图12中黑色曲线为零速包络线（LZVV），气体的注入使得LZVV在分离空间的扭曲程度升高，这是由水力旋流器内部旋流场越来越不稳定造成的，这种不稳定性一定程度上将对内流场中固体颗粒的运移产生影响。此外，随着气液比升高，LZVV逐渐往水力旋流器轴心处移动，一定程度上将更多的大密度介质通过旋流带到底流口。

2.5 分离效率

如图13-a所示，不同气液比下颗粒的分离效率差别较大，对于极细颗粒（粒径小于5 μm），分离效率主要受到伦敦色散力的影响，极细颗粒的分离效率与水的分流比呈正比[28]；当GLR过大（GLR＞40%）时，粒径为30μm的颗粒分离效率反而缓慢下降，当GLR等于50%时，粒径为30 μm的颗粒比粒径为20 μm的颗粒分离效率下降了0.01%，这是由于气液比升高增加了内流场中流体的旋转速度，使得粒径较大的颗粒反弹至内旋流通过溢流管排出，从而减小了大颗粒的分离效率。

整体而言，当颗粒直径介于5～20 μm时，分离效率随着GLR的增大而不断升高；粒径介于15～20 μm时，分离效率曲线相对于其他区域较为稀疏，因此介于该粒径区间颗粒的分离效率受气液比的影响大。如图13-a所示，随着GLR升高，分离曲线逐渐上升并向左移动。随GLR升高，切割粒径减小；然而，气液比的持续升高不会使切割粒径持续下降，当GLR为40%、50%时，切割粒径为8 μm左右，基本重合。因此，当GLR大于40%后，水力旋流器的分离效率增大不明显。

如图13-b所示，随着GLR持续升高，分离效率逐渐升高，但是当GLR超过30%以后，分离效率的增幅逐渐降低。实验结果显示，当GLR介于0～30%时，分离效率受GLR的影响显著，总分离效率由81.14%升高到91.16%，然而当GLR大于30%后，分离效率稳定在91%左右。

如图13-b所示，底流液封作用能够提高分离效率，且分离效率的变化趋势与无液封装置时一致。当GLR为0时，考虑底流液封作用影响下的分离效率与不考虑该影响下的分离效率差异最大，为7.23%，这是由于GLR为0时，再加上液封装置的应用，使空气柱完全消失，从而使得底流口过流面积增大；当GLR大于30%后，随着GLR持续升高，分离效率增幅逐渐减小，这是由于随着GLR逐渐增大，连续相中的空气逐渐析出并在中心处聚结成为空气柱，能量损失增大所导致的，另外，液封装置杜绝了空气从底流口被吸入，从而使得底流口过流面积增大而更利于固相从底流口排出。

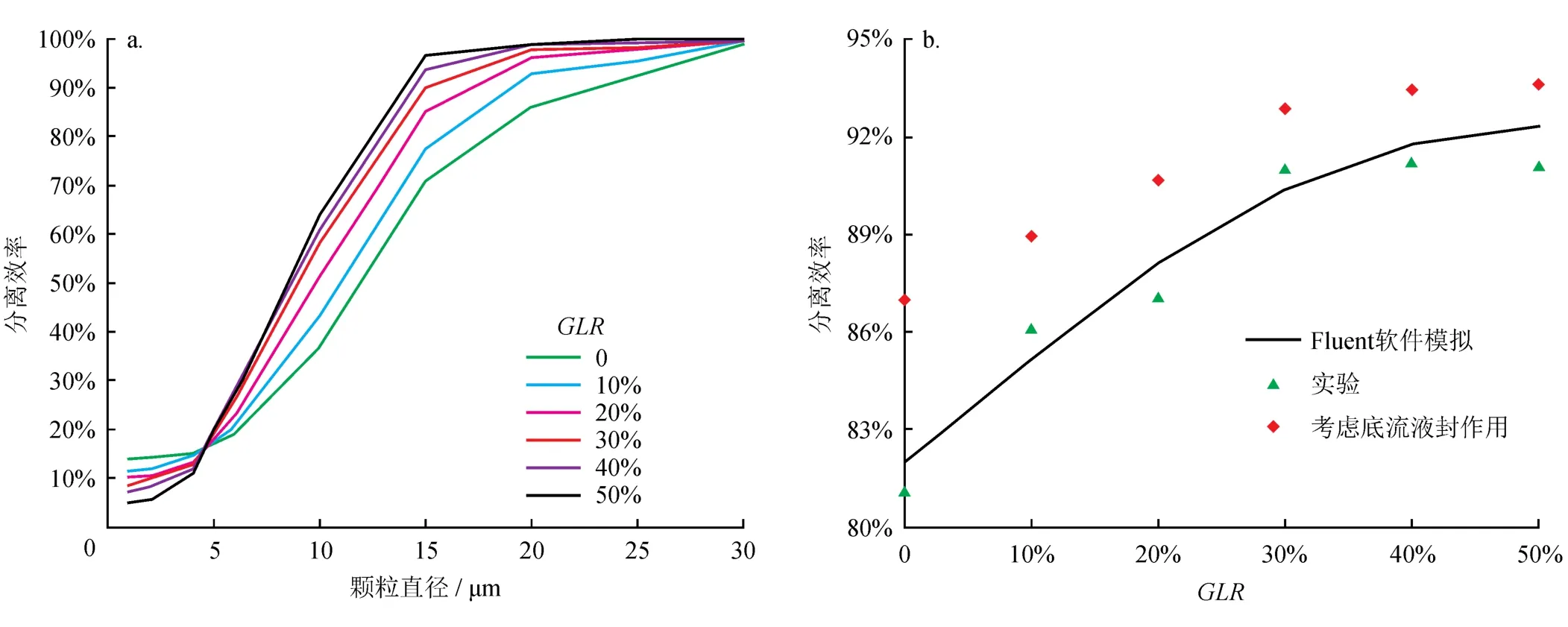
图13 颗粒直径、GLR对分离效率的影响曲线图

3 结论

1）当物料不含气体时，空气柱来源为底流口与溢流口；当物料中含有气体时，空气柱主要来源为溢流口与底流口，只有小部分来自物料；在不同GLR下，空气柱直径沿轴向变化的总体趋势相同，在锥段中部出现空气柱直径的最小值，水力旋流器柱锥交界面是GLR对空气柱直径产生不同影响的转折面。

2）随着GLR增大，壁面处压力、底流压差及溢流压差均呈非线性增长的趋势，当GLR超过40%后，由于内流场能量的损耗，压力与压差增幅变缓。

3）随着GLR增大，切向速度升高，但也使得湍流强度升高，进而影响了较小GLR条件下组合涡流场切向速度，使得组合涡流场指数减小甚至为负数，从而使得颗粒沿径向移动的力减小，不利于内流场中颗粒朝壁面方向运移。

4）随着GLR增大，轴向速度升高，且零速包络面的直径减小，一定程度上将更多的大密度介质通过外旋流带到底流口，但过大的GLR（大于40%）增加了内流场的不稳定性，影响了固体颗粒的运移轨迹。

5）GLR增大提高了水力旋流器的除砂效率并减小了切割粒径，当GLR大于40%后，切割粒径稳定在8 μm；基于水力旋流器内流场能量损失及分离效率的分析，认为入口充气条件下水力旋流器的最佳入口GLR区间介于30%～40%。