基于加权核函数SVR的时间序列预测

张翔

（同济大学电子与信息工程学院，上海 201804）

0 引言

时间序列预测问题在包括经济、工业等多个领域都有着广泛的应用，多通过历史数据建模，从而对未来的数据进行预测。本文将提出一个基于加权核函数SVR的算法来对时间序列进行预测。为了验证算法的有效性，本文使用公开数据集UCR时间序列分类数据进行时间序列预测。结果表明，加权核函数SVR对时间序列具有良好的预测性能。

1 时间序列预测

针对时间序列的预测目前主要有两种方法，第一个是统计学方法，目前最常用的模型是在AR模型和MA模型结合的ARMA模型的基础上，提出通过使用差分序列的方法解决非平稳问题的ARIMA模型[1]。在ARIMA模型的基础上，文献[2]提出了结合ARMA模型和分数维差分噪声模型（FDA）的分整自回归移动平均模型（ARFIMA）。这一模型对于长短期时间数据都有一定的表达能力。

第二个就是机器学习的方法，随着人工神经网络（ANN）被提出，研究者们发现，其对复杂环境数据的表达能力非常强，所以提出通过ANN对时间序列进行预测[3]。例如，文献[4]利用回归神经网络进行外汇和交易误差的修正，而回声状态网络[5]被用来实现股票数据挖掘。文献[6-7]通过SVM对金融时间序列进行预测对金融时间序列以及股票进行了预测，并证明了其有效性。

SVM[8]自从被Vapnik提出来就表现出了优秀的计算效果。SVM被用于回归问题的模型被称作支持向量回归（SVR），在解决非线性问题时可以将其转换为高维空间中的线性问题，通过核函数的计算代替高维空间的复杂计算，是一个非常有效的方法。

2 加权核函数SVR算法

SVM模型即为在高维空间中计算得到一个超平面来对样本点进行区分。对于线性可分的问题，SVM的分类超平面公式可以表示为：

分类超平面为了在尽量多的数据上保持分类效果，就必须使训练集的分类间隔最大化，这也是SVM的核心思想。目标函数计算公式为：

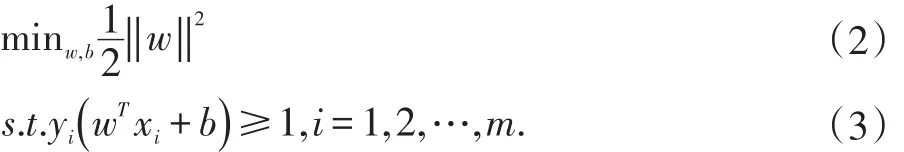
其中w=(w1,w2,…,wd)为法向量，可以决定了超平面的形状；b为差异量，可以决定超平面的位置。

SVR的概念是SVM用于解决回归问题时提出的模型。在SVM中，只有f（x）和y完全相同时，认为成立。而SVR使用了ϵ不敏感损失函数，只要f（x）和y的误差在ϵ之内就认为是无损失的，当误差绝对值大于ϵ时，计算其损失减去ϵ。目前SVR被认为是解决机器学习回归问题的有效方法。

SVR的问题可以形式化为公式（4）。

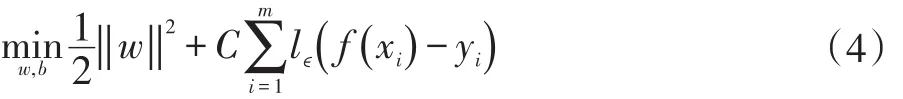
其中，C为正则化常数，lϵ为ϵ不敏感损失函数，lϵ计算公式如公式（5）。

引入松弛变量 ξi和 ξi，公式（5）可重写为公式（6）。

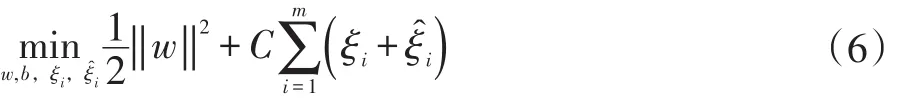
本文提出一种基于加权SVR的时间序列预测方法，一般的机器学习加权方法都是对于样本的重要程度进行加权，但是对于一条时间序列而言，经过滑动窗口划分获取数据集，每一个样本之间不存在重要程度的差别，而对每一个样本，时间点的远近对回归结果有较大的影响，所以更适合使用对特征进行不同权重的计算。

加权核函数的定义为：

P为给定输入特征空间的n阶矩阵。我们针对不同特征赋予不同权值，这种情况下，P即为对角矩阵。所以加权核函数定义如下式：

（1）加权线性核函数：

（2）加权多项式核函数：

（3）加权高斯径向基核函数：

核函数通过非线性特征的映射的方法，将特征空间中的非线性特征转换为线性特征，同时降低运算难度。P为线性特征映射，用来对线性特征的维度进行缩放，不改变特征的线性特性。

本文运用CART算法来计算每个特征的加权权重。CART算法的主体是对基尼指数的计算。基尼指数是一个样本被分类分错的概率。针对一个特征的属于一个状态中的所有样本在分类时归属类别少时（甚至只属于一个类别），基尼指数最小，此时特征区分能力越强。通过计算决策树节点分支前后基尼指数变化差值来计算该特征重要性。特征个数为c，基尼指数计算公式如公式（11）：

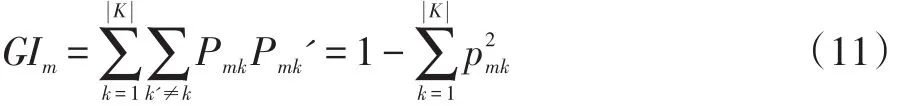
m为决策树中的某一个节点，K为最终分类个数，Pmk为节点m中类别K样本所占比例。特征j在节点m的重要性计算方式为该节点分枝前的基尼指数前去分枝后左右子节点基尼指数，计算公式如式（12）。

GIl和GIr分别为分支后左右子节点基尼指数。然后针对整个随机森林，统计特征j在第i棵决策树的特征重要性，计算公式如式（13）。

最后计算n个决策树对于特征j的重要性之和，即为特征重要性。但是在应用时需要对每个特征重要性进行归一化，使其表示为每个特征对决策的影响，计算公式如式（14）。

所有特征的特征重要性组成一个对角矩阵，成为SVR核函数加权的矩阵。

3 实验分析

实验数据采用UCR时间序列分类数据集[9]，该数据集含有八十余个时间序列数据，目前有超过一千篇时间序列预测相关论文使用该数据集进行实验，该数据集是目前时间序列预测实验的基本数据集。我们从中抽取了10份时间序列数据用于时间序列预测相关实验。数据集如表1所示。于时间序列预测是针对两条相关序列的误差进行判断，所以我们使用对均方根误差（Root Mean Squared Error，RMSE）和平均绝对百分比误差（Mean Absolute Percent Error，MAPE）来进行评估。

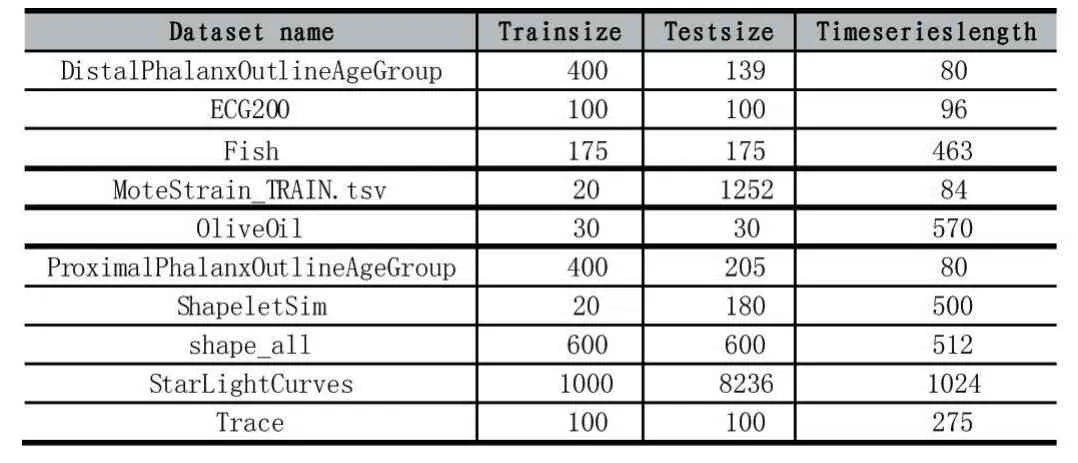
表1 UCR时间序列分类数据集

均方根误差是真实值和预测值偏差的平方和观测次数比值的平方根。均方根误差表示的是真实值和预测值之间的偏差，代表了时间序列的绝对误差。平均绝对百分比误差是真实值和预测值偏差除以真实值的百分比，是误差和真实值之间的比值，代表了时间序列的百分比误差。预测的误差越小，代表预测越准确。

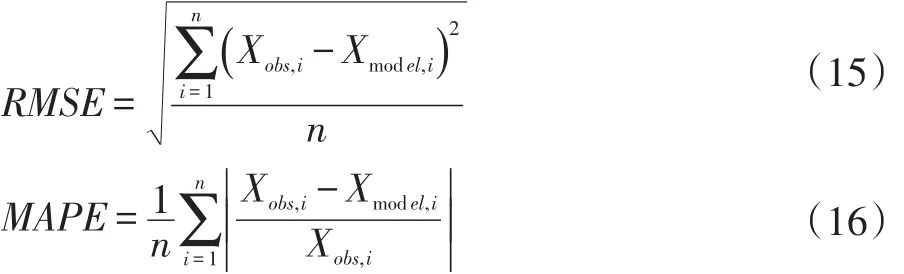
本文使用两组实验，分别为对三种不同加权核函数效果进行对比，加权核函数SVR和不加权核函数SVR的效果对比，验证了模型的有效性。

首先使用线性核函数、多项式核函数和高斯径向基核函数对加权SVR的效果进行评估，分别计算其RMSE和MAPE。实验结果如表2和表3所示。

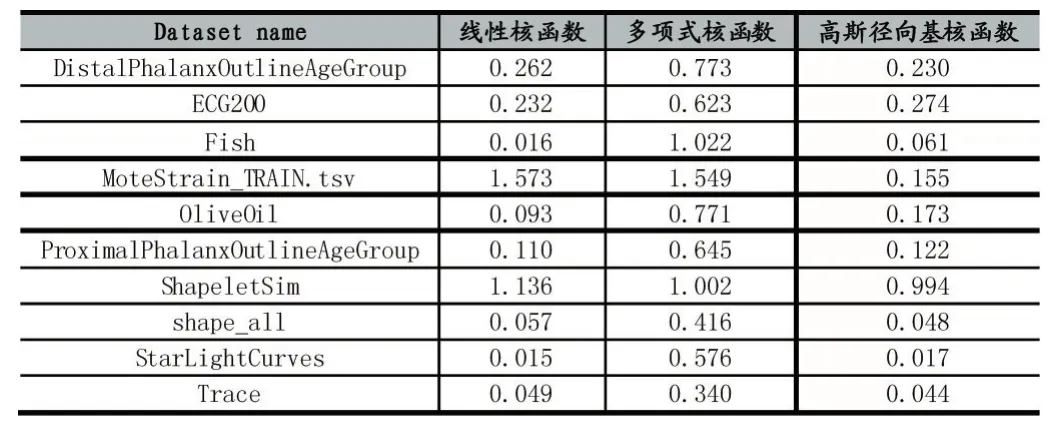
表2 不同加权核函数RMSE

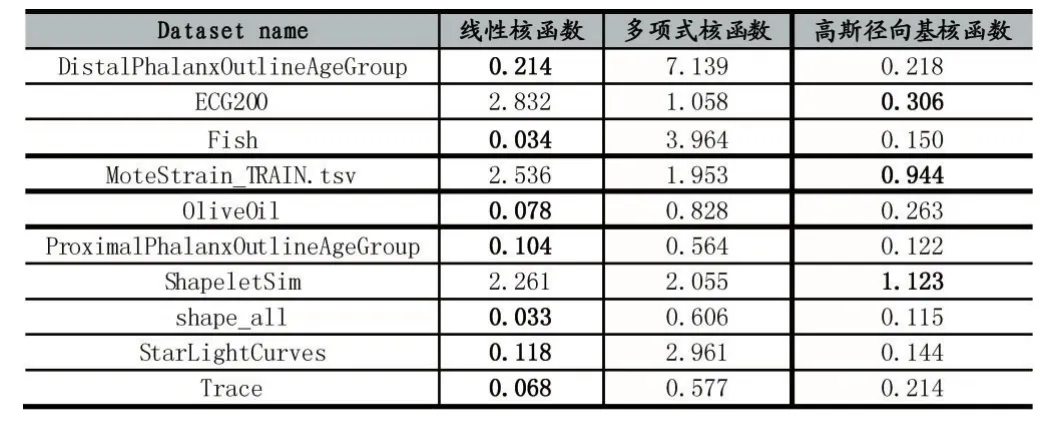
表3 不同加权核函数MAPE

表中加粗数级即为该行最小值。由表2和表3可以看出，线性核函数和高斯径向基核函数的RMSE和MAPE均小于多项式核函数。对于所有数据计算得到，线性核函数的RMSE和MAPE平均值分别为0.3542和 0.8277，高斯径向基核函数的 RMSE和MAPE平均值分别为0.2118和0.3597。

线性核函数对于所有数据集预测结果的RMSE最优误差有5个，MAPE最有误差有7个，但线性核函数的两个平均误差均大于高斯径向基核函数，这表示线性核函数虽然对较多数据集有最优效果，但是在个别数据集效果极差，所以高斯径向基核函数的平均性能最优，对于多种数据的平均拟合情况最好。

可以看出线性核函数和高斯径向基核函数的加权SVR表现出较好的预测效果，我们再比较两个核函数对于不加权SVR的效果。表4和表5分别为不加权核函数SVR的RMSE和MAPE。

表4 不加权核函数的RMSE

表5 不加权核函数MAPE

对加权和不加权的两种方法的线性核函数对比作图。为方便查看不同数据集数据，将数据归一化，不加权两个误差归一到1，加权误差等比例缩放。如图1。

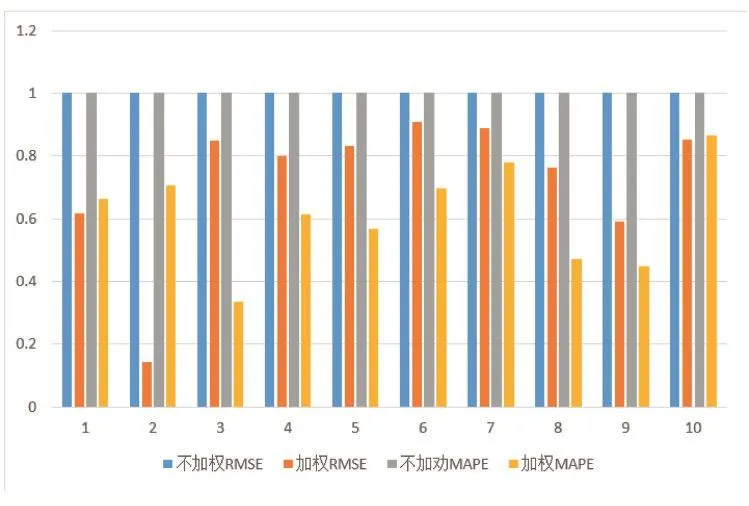
图1 线性核函数SVR和不加权线性核函数SVR误差对比图

对加权和不加权的两种方法的高斯径向基核函数对比作图。作图方法同上。如图2。

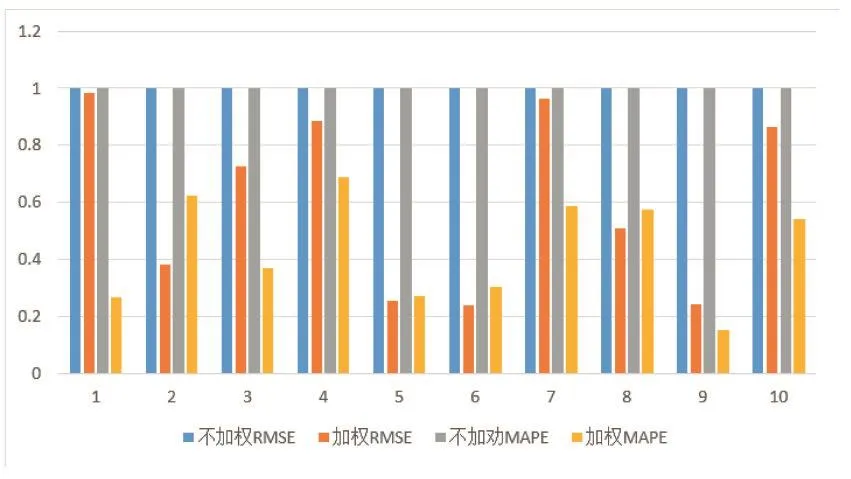
图2 高斯径向基核函数SVR和不加权高斯径向基核函数SVR误差对比图

由图1和图2可明显看出两个核函数加权方法对时间序列预测效果不同程度的提高。

4 结语

本文介绍了一种基于加权核函数SVR的时间序列预测的方法，通过随机森林CART的特征重要性计算方法对特征赋予权值，这样在时间序列预测时可以对不同时间段有不同的侧重，这样改变特征维度的广度变化，从而影响预测结果。可以由以上实验看出，该方法在SVR的基础上有一定的提升。