基于GA-SVM的GNSS-IR土壤湿度反演方法

孙波， 梁勇,*， 汉牟田， 杨磊， 荆丽丽， 俞永庆

(1. 山东农业大学信息科学与工程学院, 泰安 271019； 2. 北京航空航天大学电子信息工程学院, 北京 100083； 3. 中国石油化工股份有限公司胜利油田分公司海洋采油厂, 东营 257237)

土壤湿度是全球碳水循环的重要环节，是量化陆地及大气能量交换的关键参数[1]。及时、准确地获取农田土壤湿度数据对于在农业生产中进行合理灌溉、减少水资源浪费、降低生产成本和提高农作物产量都是非常重要的。

相比于传统的烘干称重法以及时域反射法(TDR)、频域反射法(FDR)等接触方式获取土壤湿度的方法[2]，利用全球卫星导航系统反射测量法(Global Navigation Satellite System Reflectometry, GNSS-R)技术进行土壤湿度探测是一种新兴的技术手段，其具有非接触、大面积、实时性、连续性的优点，近年来受到越来越多的关注。

1993年，欧洲航天局(ESA)的Martin-Neira[3]首次提出了利用GNSS-R信号可以进行海面测高的技术。随后，科罗拉多大学与美国国家航空航天局(NASA)合作研制了GNSS-R接收处理设备，并开展了一系列机载实验，探索该技术用于土壤湿度探测的可行性。近年来，Rodriguez-Alvarez等[4]在GNSS-R技术的基础上提出可以利用卫星直射信号和多径信号的干涉现象进行土壤湿度探测的方法，称为干涉图技术(Interference Pattern Technique，IPT)，也称为全球卫星导航系统干涉测量法(Global Navigation Satellite System Interferometry and Reflectometry，GNSS-IR)。Larson等[5]指出GNSS接收机记录的信噪比(Signal to Noise Ratio，SNR)数据受多径信号的影响呈现出衰减振荡特征，该特征是干涉现象的表现，其通过实验证明信噪比数据的振荡振幅和相位与土壤湿度有关。Chew等[6]在此基础上建立了信噪比相位和土壤湿度的经验模型，可以用来反演裸土表层的土壤湿度。2018年，李飞等[7]对镜面反射点、空间分辨率和土壤探测深度进行了理论分析和公式推导。2018年，严颂华等[8]探讨了基于信号强度指示器(SSI)数据的土壤水分估算的可行性，并进行了SSI相位估算和原位土壤水分数据记录的实验比较。在植被影响研究方面，张思勃等[9]考虑小麦不同生长阶段的影响，建立了土壤湿度与信噪比振荡频率和相位的经验模型。

然而，上述经验反演模型的建立均假设土壤湿度与信噪比幅度、相位等观测量呈线性关系，因此模型建立过程多采用传统的一元统计回归方法，其反演结果的相关系数介于0.76～0.90之间[10-12]，反演精度不高。而机器学习等人工智能算法的兴起，使得复杂回归模型的建立成为可能。杨磊等[13]探索了机器学习方法在GNSS-R土壤湿度技术中的应用，取得了较好的结果。机器学习方法具有黑箱特征，不用指定回归函数的形式，可以进行任意的线性或非线性回归，并且隐含实现了特征提取的环节，可以对土壤粗糙度等引起的噪声进行抑制，在不出现过拟合的情况下，其效果是传统的统计回归方法不可及的。

本文提出使用支持向量机(Support Vector Machine，SVM)这一机器学习方法，进行GNSS-IR土壤湿度反演模型建立，特别地，采用遗传算法(Genetic Algorithm，GA)解决SVM的参数自动优选问题，并通过实测数据处理，证明该方法可取得较好的结果。进一步与统计回归及其他机器学习方法进行比较，证明了GA-SVM方法在同等条件下效果更优。

1 GNSS-IR土壤湿度反演原理

相比于传统的GNSS-R反演模式，GNSS-IR模式只采用一根右旋圆极化(Right Hand Circular Polarization，RHCP)天线同时接收GNSS的直反射卫星信号，GNSS发射的信号为RHCP信号，根据电磁波反射理论，当地面为不含磁性成分的土壤介质时，在卫星高度角θ较低的情况下，反射信号极性仍以RHCP为主[14]，其场景如图1所示。

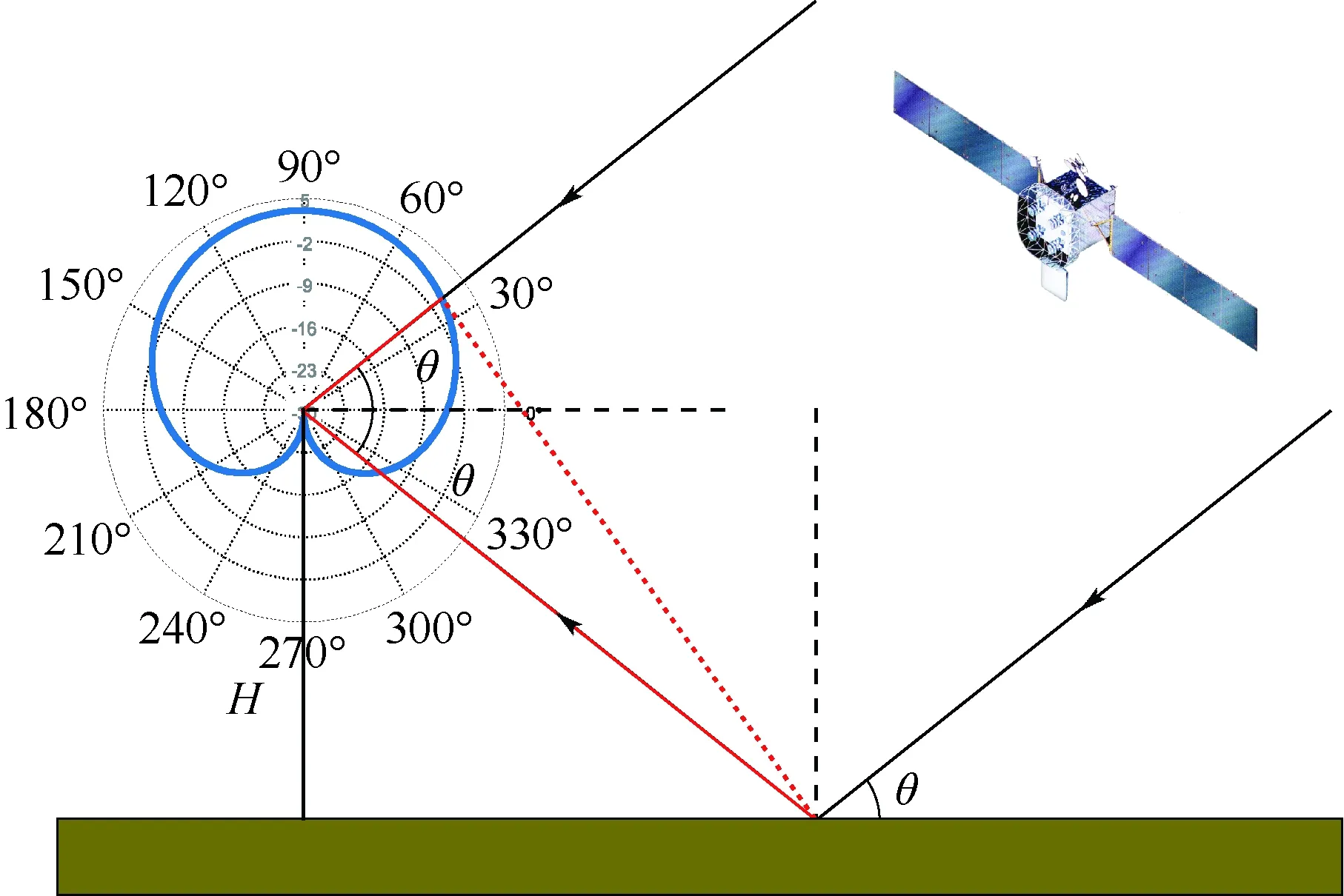
图1 干涉场景Fig.1 Scenario of interference

在传统的卫星信号接收中，通常把多径反射信号当作干扰进行抑制，但实际上反射信号与反射面的物理特征如土壤湿度具有相关性。由于地基情况下直射跟反射信号频率近似相同，只是传播路径长度不同，因此2个信号可在接收天线处发生较为稳定的干涉现象，形成干涉信号,如图2(a)所示。可以看出，在低高度角时，干涉波动现象十分明显。该信号经接收机接收处理后以信噪比数据的形式呈现出来。信噪比的数学模型[15]为

(1)

式中：Ad、Am分别为直射、反射信号的幅度；ψ为直射信号和反射信号的相位差。

则有

(2)

式中：φ1为直反射路径差导致的相位差；φ0为干涉初始相位；H为接收机天线的等效高度，其随着电磁波的穿透深度和反射面的介电特性的变化而变化；λ为GNSS卫星信号的波长。

通过式(2)，可以得到多径振荡的频率为

(3)

考虑在每天信噪比观测的几小时时间内，天线等效高度的变化率可以忽略不计，并进一步令x=sinθ，式(3)可简化为

(4)

式(4)说明H与f成线性关系，天线越高，振荡频率越高。结合式(1)～式(4)，将直射信号剔除，只保留与反射面参数有关的多径信号，如图2(a)、(b)所示。该多径信号SNRm可以表示为

SNRm=Amcos(4πHλ-1sinθ+φ)

(5)

式中：φ为多径信号的初始相位。

通过对SNRm信号进行谱分析，可以获得多径信号的振荡频率f和天线等效高度H，如图2(c)所示。由于SNRm信号是非均匀采样信号，常规的傅里叶分析并不适用，引入Lomb-Scargle方法[16]对SNRm进行谱分析， Lomb-Scargle方法能够提供一种针对不均匀采样时间序列的谱幅值计算方法，可以处理非均匀采样的信号。

图2 上升段信噪比分析Fig.2 Ascending SNR analysis

此后通过最小二乘法对SNRm进行拟合，可以得到多径信号的幅度Am和初始相位φ，如图2(b)所示，并分别建立振荡频率、幅度、相位和土壤湿度之间的经验模型。

2 GA-SVM土壤湿度反演模型

文献[10-12]提出建立一元线性回归模型进行土壤湿度的反演，然而考虑到振荡频率、幅度、相位与土壤湿度的相关性，采用多元回归模型可以有效利用特征信息，充分利用它们之间的相关性，提高拟合精度，本文采用非线性SVM模型进行土壤湿度的反演研究。

SVM是20世纪90年代由Vapnik[17]提出来的一种研究小样本、小概率事件的神经网络模型,可以根据有限的样本信息在模型复杂性和学习能力之间寻找最优解, 以获得最好的预测精度, 其在解决小样本、非线性和高维学习中表现出许多特有的优势，而土壤湿度反演本质上是一个回归问题，适合选用SVM算法进行回归分析。

SVM利用核函数映射的方法，通过非线性映 射将已知空间变换到高维空间，从而利用解线性问题的方法求解非线性问题。本文中采用径向基(Radial Basis Function,RBF)核函数来建立非线性 SVM模型。RBF核函数相比于线性核能够处理分类标注和属性的非线性关系，相比于多项式核有更少的参数，同时具有简单实用、普适性好的优点[18]。并且根据实践证明，SVM的性能与核函数的参数g以及惩罚因子C有很大关系，人为规定和调整参数的话，既耗费时间又不能确保预测结果的准确性，因此，本文引入了GA对SVM回归模型的参数进行自动寻找最优解。

遗传算法是 Holland[19]于1975年提出的一种基于生物遗传和进化机制的、适用于复杂系统优化的自适应概率优化技术。该算法是借鉴进化生物学中遗传、突变、自然选择、杂交等现象而探索出的一种搜索最优解方法，主要包括编码、初始种群、计算适应度以及选择、交叉、变异3个基本运算。与传统优化算法相比，GA寻优具有以下特点：①搜索效率高，以群体为单位，对自变量中所有个体进行并行搜索；②可进行全局最优解搜索，避免陷入局部最优解；③不受目标函数影响，适应性强。

基于GA-SVM的GNSS-IR土壤湿度反演模型建立过程如图3所示。

图3 基于GA-SVM的GNSS-IR土壤湿度反演模型Fig.3 GNSS-IR soil moisture inversion model based on GA-SVM

3 实验与结果分析

3.1 实验数据采集

实验场地位于法国图卢兹(Toulouse)市拉马斯克雷(Lamasquere)镇的一处农场(北纬 43°29′14.45″，东经1°13′44.11″)，实验田种植作物为大豆。2014年2月3日—2014年3月21日进行了为期47 d的土壤湿度探测实验。实验期间该地区正处于冬季，日平均降雨量仅为1.19 mm，地表植被稀少，可以视为裸土，且场地四周无遮蔽。土壤表面均方根高度约为0.02 m，反射区域2～5 cm深度的土壤成分为:沙土18%，粉土41%，黏土41%。使用Leica GR25接收机和AR10基准站天线，同时接收GPS的直射、反射信号，天线的架设高度为1.69～1.70 m，相位中心指向天顶。距离天线相位中心在地表投影约2 m的位置采用填埋方式布置2枚ML3 Theta Probe土壤湿度传感器采集土壤湿度同比数据，2枚传感器深度分别为2 cm和5 cm，精度为±1%，取样间隔时间为2 min。本文选取干涉现象明显的2°～30°低高度角的L1波段S1C SNR信号进行土壤湿度反演。

3.2 反演模型建立

3.2.1 样本数据的选取

选取观测效果较好的GPS PRN 12的SNR数据按照第1节的原理进行处理，得到47组与土壤湿度具有相关性的多径信号的初始相位φ、振荡频率f、幅度Am，结合卫星高度角θ，与实测的2 cm与5 cm深度的土壤湿度日平均值形成SVM数据集，这47组数据对应的传感器土壤湿度实测平均值范围为23.24 ～29.45 cm3/cm3。为了消除各影响因素因类型及量纲不同带来的影响，对输入变量均做归一化处理。将这47组数据按照约3∶1的比例划分成训练集与测试集，训练集与测试集互斥，没有交集，将传感器测量的日平均土壤湿度作为SVM的输出。

3.2.2 GA-SVM模型训练

本文SVM模型选用普适度较好的RBF核函数，并采用GA对其进行参数寻优。为了提高反演模型的精度及泛化能力，对核函数参数g和惩罚因子C进行优选是关键。GA的相关设置如下：最大进化代数为200，种群数量为20，惩罚因子C的取值范围为[0,100]，核函数参数g的取值范围为[0,1 000]，交叉验证次数V=5。寻优过程的适应度曲线如图4所示。可以看出，经过30次进化迭代后，种群最佳适应度基本保持稳 定，可以认为近似达到最优解。最终寻优结果为:C=3.23，g=0.08，适应度MSE=0.045。

图4 GA-SVM进化代数曲线Fig.4 Evolution algebra curves of GA-SVM

3.3 结果分析

将最佳参数C和g代入SVM模型，选取GPS PRN 12卫星的前35 d数据和土壤湿度真值作为训练集，对后12 d的土壤湿度进行预测反演，所得结果如图5所示。

图5(a)～(c)显示训练样本预测值与土壤湿度实测值具有很好的相关性,误差控制在±0.5 cm3/cm3之内，决定系数R2达到了0.882 7。图5(d)～(f)表明利用训练后的GA-SVM模型可以对测试样本进行较好的反演，反演结果接近实测值，反演误差控制在±0.3 cm3/cm3之内，没有出现偏态分布，反演值与实测值的线性回归方程决定系数R2达到了0.956 9。在图5(d)～(f)中，还进行了GA-SVM方法与传统的利用SNR频率、幅度、相位的一元线性回归方法的对比，结果表明，本文方法的反演结果更接近实测值，误差较小，相比于单变量反演效果最好的相位反演(R2=0.874 7),决定系数R2提高了约9.40%，说明GA-SVM优化模型反演精度高，泛化能力较强。

为了进一步验证GA-SVM模型的优越性，在使用同一数据样本的条件下，本文还与粒子群优化的SVM模型(PSO-SVM)、反向传播(BP)神经网络这2种机器学习方法进行了对比，表1给出了对比结果。

图5 GA-SVM土壤湿度反演模型结果分析Fig.5 Result analysis of GA-SVM soil moisture inversion model

日期实测值/(cm3·cm-3)GA-SVMPSO-SVMBP神经网络反演值/(cm3·cm-3)绝对误差/(cm3·cm-3)相对误差/%反演值/(cm3·cm-3)绝对误差/(cm3·cm-3)相对误差/%反演值/(cm3·cm-3)绝对误差/(cm3·cm-3)相对误差/%2014-03-1025.8325.76-0.070.2726.140.311.2026.520.692.672014-03-1125.5525.41-0.140.5526.180.632.4726.951.405.482014-03-1225.2125.10-0.110.4425.300.090.3627.091.887.462014-03-1324.5524.850.301.2225.721.174.7724.950.401.632014-03-1424.4524.640.190.7825.380.933.8024.990.542.212014-03-1524.2724.480.210.8724.870.602.4724.440.170.702014-03-1624.0724.240.170.7124.240.170.7125.231.164.822014-03-1723.9724.180.210.8823.990.020.0825.471.506.262014-03-1823.8323.990.160.6723.940.110.4624.100.271.132014-03-1923.8823.71-0.170.7124.620.743.1024.660.783.272014-03-2023.6223.58-0.040.1724.060.441.8625.551.938.172014-03-2123.2423.490.251.0823.620.381.6424.361.124.82

表2 土壤湿度反演结果评价比较

4 结 论

本文提出了基于GA-SVM优化模型的GNSS-IR土壤湿度反演方法，给出了数据处理的相关流程，并通过实测数据进行了理论验证，结果表明：

1) 在土壤湿度介于23.24～29.45 cm3/cm3范围内，反演值与高精度土壤湿度计测得的实测值的相关度较好，线性回归方程决定系数达到了0.956 9，反演误差控制在±0.3 cm3/cm3之内。

2) 与传统利用相位等进行一元线性回归的方法相比，决定系数提高了约9.40%，进一步验证了GA-SVM优化模型的有效性。

3) 在相同数据集下，与PSO-SVM、BP神经网络的对比结果表明，本文模型各项误差较小，说明其更适用于小样本条件下GNSS单天线的土壤湿度反演，具有较好的普适性。

本文为土壤湿度的遥感监测提供了一种新的思路和方法。由于季节所限，本次实验及数据分析都是基于裸土的土壤湿度分析，地表植被和农作物对土壤湿度的影响并未进行修正，这也是后续实验研究的主要内容。

致谢感谢法国CESBIO实验室的Baup和Boniface博士收集的气象数据，感谢法国图卢兹第三大学的Roussel和Frappart博士提供的GNSS观测数据,同时感谢金华职业技术学院阮宏梁老师在实验中提供的支持。