基于RNN 的智能网联汽车高精度定位方法

李晓晖，方 芳，邓天民

（1.重庆西部汽车试验场管理有限公司，重庆 408300；2.重庆交通大学 交通运输学院，重庆 400074）

智能网联汽车作为 “互联网+” 在汽车上的应用，具有安全、舒适、节能、高效行驶、可替代人操作等优点。然而智能网联汽车的运行环境复杂，运行过程多变，对高精度定位提出了更高的要求。因此，组合导航定位是未来智能出行的关键因素之一。

组合导航是非线性系统，针对非线性系统问题，熊剑等[1]、王硕等[2]利用高斯滤波算法提高了定位精度，增强了预测的实时性，但是没有针对噪声进行具体分析。针对组合导航过程噪声和量测噪声的不确定性问题，王维等[3]、王慧丽等[4]、房德君[5]分别运用了无迹卡尔曼滤波方法、不确定融合估计的GPS/INS（Global Positioning System and Inertial Navigation System）滤波算法和自适应卡尔曼滤波方法进行试验验证，证明了其实用性和良好的鲁棒性，但是缺少对INS 滤波的具体分析。针对GPS/INS 组合导航中INS 建模的问题，李增科等[6]、徐爱功等[7]分别提出了一种基于牛顿插值的GPS/INS组合导航惯性动力学多阶建模算法和基于小波降噪的GPS/INS 紧组合方法，提高了系统的精度和稳定性，但是缺乏对GPS 信号失效定位精度的分析。针对GPS 中断问题，谭兴龙等[8]、胡方强等[9]针对GPS/INS 组合系统中GPS 中断时，导航性能会急剧降低的情况，分别提出了改进径向基神经网络结合自适应滤波辅助的组合系统导航算法和改进的自适应卡尔曼滤波方法，试验证明了其有效性。

卡尔曼滤波的相关方法较为成熟、性能良好，但是针对GPS 失效问题，卡尔曼滤波方法在定位高精度性和实时性上效果有待提高。周邵磊等[10]提出了单目视觉ORB-SLAM/INS 组合导航方法，通过初始化阶段利用ORB-SLAM 方法计算的尺度因子修正惯导系统的误差。焦雅林等[11]提出了基于改进粒子滤波算法的GPS/DR 车辆组合导航信息融合技术，其滤波性能明显优于扩展卡尔曼滤波（Extended Kalman Filter，KEF）。李士心等[12]利用非线性滤波方法，强跟踪滤波渐消因子加入容积卡尔曼滤波中，提出了捷联惯导/里程计组合导航的自适应强跟踪滤波算法，达到了惯性原件的理论精度。

但是，随着人工智能的发展和计算机水平的提高，神经网络方法用于导航定位成为研究重点与热点。循环神经网络（Recurrent Neural Network， RNN）具有极强的非线性动态映射能力和动态记忆功能，适用于动态过程建模，实现动态系统预测。

冯永等[13]提出一种携带历史元素的RNN 推荐模型负责用户短期动态兴趣建模，并结合前馈神经网络（Feedforward Neural Networks，FNN）构建了多神经网络混合动态推荐模型（Hybrid Dynamic Recommendation Model Based on Multiple Neural Networks，MN-HDRM），在多项评价指标上具有优越的性能。张国兴等[14]将SDZ（Surprisal-Driven Zoneout）应用于RNN 并提出了基于SDZ-RNN 的出租车目的地预测方法。该方法有效地缩短了训练时间，提高了预测精度。ORDÓÑEZ 等[15]分析了森林环境中GPS 测量的准确性，应用RNN 建立一个将观测误差与GPS 信号相关联的数学模型，RNN网络效果良好。NAKHAEI 等[16]比较3 种类型的人工神经网络，即径向基函数神经网络（Radial Basis Function Neural Network， RBFNN）、RNN 以及多变量非线性回归（Multiple Non-Linear Regression， MNLR）模型来预测浮选柱的冶金性能，对比了其训练能力和准确性。

因此，本文提出了一种基于RNN 的高精度定位模型，该模型通过大量精确的GPS/INS 数据进行训练。当GPS 失效时，训练好的模型预测失效时的定位信息，有效提高了组合导航的定位效果。

1 高精度定位方法

1.1 RNN 网络模型

RNN 是传统前馈神经网络（FNN）的一种变体。 RNN 和FNN 之间的区别在于FNN 的神经元仅通过层和层之间的连接来传递信息。虽然RNN 在网络中引入了环形结构，但它建立了神经元与自身的连接。通过这种连接RNN 可以将网络中最后一个时间点的输入存储为“存储器”，并在下一步中影响网络输出。对于FNN，只能将输入通过隐藏层映射到输出层，而RNN 可以将整个历史记录映射到每个输出神经元。因此，在输入和输出都是序列数据的预测问题中，RNN 比FNN 具有更好的性能[17]。

RNN 的预测过程类似于FNN，其由前向传播算法完成。FNN 的训练过程是通过反向传播实现的，而RNN 需要通过时间维度和反向传播时间（Back Propagation Through Time，BPTT）叠加反向传播的结果，因为不同时间步长之间会相互影响。通常，循环神经网络是推测或完成信息的不错选择。因此，本文采用基于RNN 的状态空间模型来描述智能联网车辆的驱动过程。RNN 的结构如图1 所示。它有3 层，即输入层、隐藏层和输出层[18]。

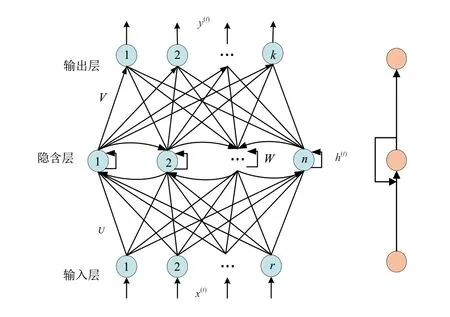
图1 RNN 网络结构

RNN 的数学模型为：

式中：t表示t时刻；x(t)表示输入层输入；h(t)、ht()-1分别表示t时刻和t-1 时刻的隐含层输出；φ(为隐含层激活函数，一般选择tanh 函数；o(t)表示输出层输入；表示输出层输出；σ(为输出层激活函数，这里采用纯线性Pureline 函数；U表示输入层到隐含层的连接权值；W、b分别为隐含层之间的连接权值和偏置；V、c分别为隐含层与输出层连接权值和偏置。

1.2 基于RNN 的训练模型

（1）样本集预处理

采用最大最小归一化方法对投影处理后的样本进行归一化处理，如式（6）所示。

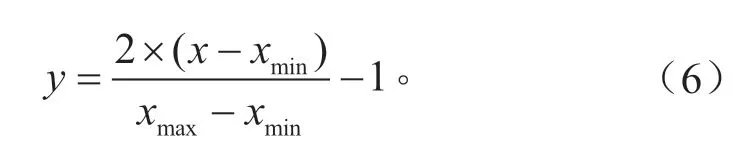
式中：x，y分别表示原始数据和归一化后的数据；xmax，xmin分别表示x的最大值和最小值。训练数据通过归一化后保留其最大值、最小值、平均值等信息，用于失效预测模型中神经网络输入数据的归一化及其输出数据的反归一化。

（2）对RNN 模型进行训练，训练过程如下。输入层的输入、输出分别为：

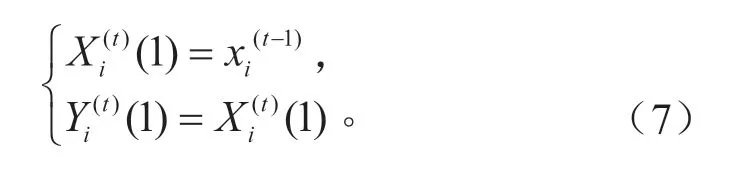
隐含层的输入、输出分别为：

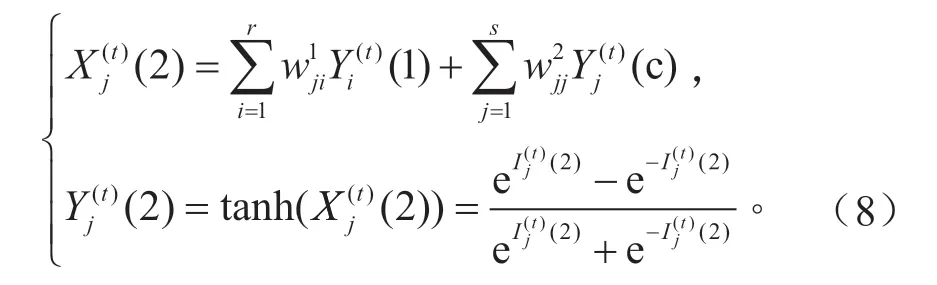
输出层的输入、输出分别为：

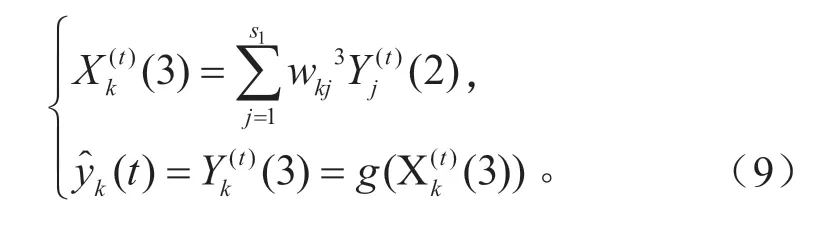
1.3 基于RNN 的GPS 失效定位模型

假设GPS 失效时，该时刻记为t0，前一时刻经纬度为令T为失效时长，f为数据采集频率，则预测步数η= ×T f，预测轨迹及误差为：

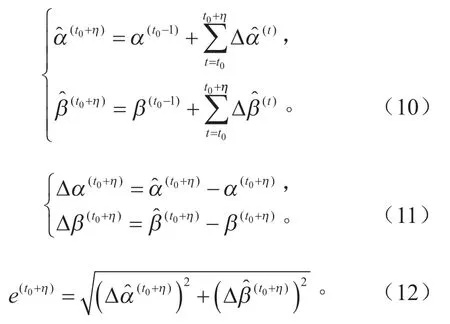
2 试验

2.1 数据采集系统

本文基于GPS/INS 组合导航系统，结合RNN模型来实现智能网联汽车全域的高精度定位，其系统结构如图2 所示。

图2 GPS/INS 定位系统结构

定位系统通过BD/GPS 天线接收卫星，然后通过①的放大和变频处理传输到BD/GPS 接收机中，通过接收机结合RTK 基站的差分信号得到时间、经度、纬度、高程等定位信息；然后通过②将定位数据中的经度、纬度以及INS 采集的速度和姿态角进行归一化处理，作为神经网络的输入，通过③进行模型训练得到预测的经度、纬度增量；结合④中的上一时刻真实的定位数据，通过⑤输出预测的下一时刻定位数据。在卫星信号正常阶段，针对模型进行训练，⑤输出的预测定位经纬度与⑥传输的当前时刻真实定位经纬度相对比，得到其误差，从而不断修正神经网络的参数。当不能正常接收到卫星信号时，通过②～⑤即可得到预测的高精度定位数据。

2.2 试验数据及模型

数据采集使用Vbox 系统，自建Vbox-RTK 差分基站，使用48 MHz 电台通讯，数据采样率为100 Hz，经过整理后约有37 万组有效数据。

根据数据的特性，构建两种不同的神经网络模型，其中模型1 使用BP 神经网络，模型2 使用RNN。两个模型输入均为速度、航向角、俯仰角和横滚角，输出为经度增量和纬度增量，隐含层为含有15 个神经元的网络结构。模型结构如图4 所示。

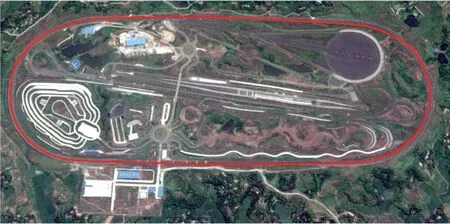
图3 数据采集区域卫星图

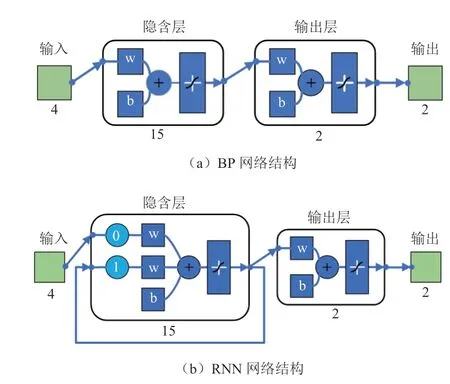
图4 BP 神经网络和RNN 的模型结构

3 讨论与分析

3.1 预测误差分析

基于训练完成的BP 神经网络和RNN 高精度定位模型，使用40 000 余组测试样本分别进行测试，从而获得预测纬度增量和预测经度增量。将预测经纬度增量与测试样本经纬度增量分别进行比较，其经纬度增量误差曲线如图5 所示，误差数据统计量对比见表2。

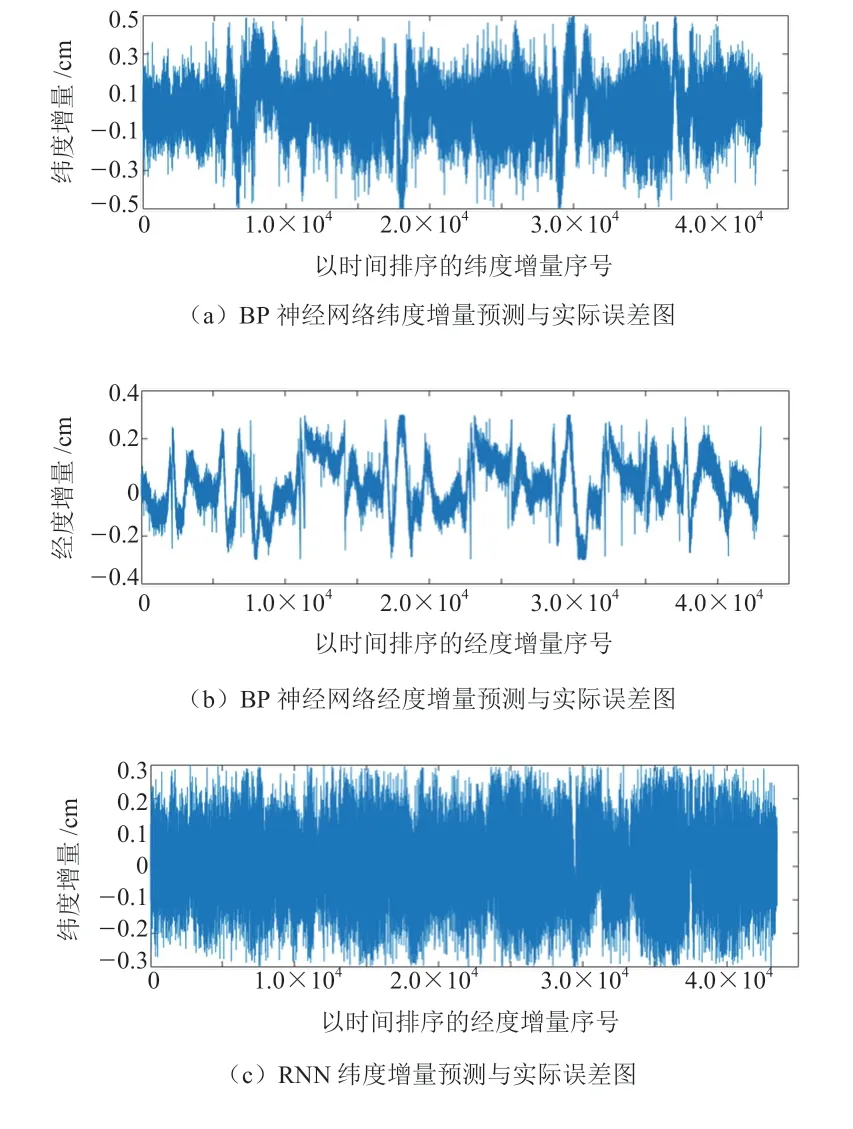
图5 预测经纬度增量误差曲线

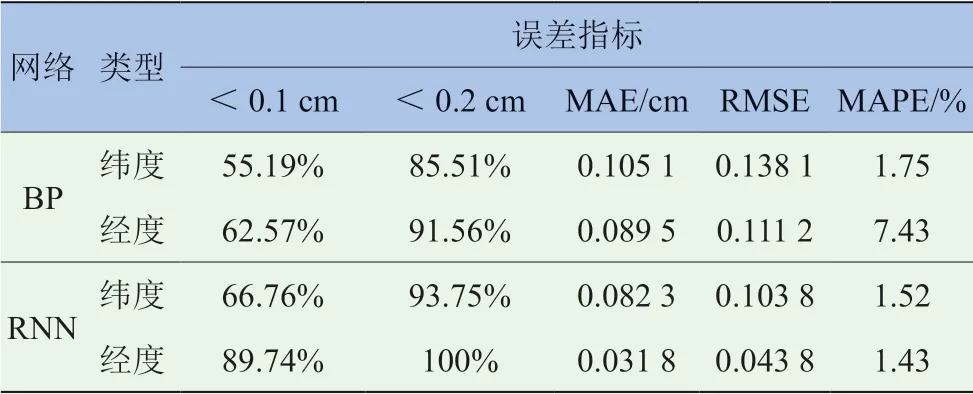
表2 网络预测误差指标对比

由图5 和表2 可知，BP 神经网络绝对误差均小于0.5 cm，85%绝对误差小于0.2 cm；RNN 经纬度绝对误差均小于0.3 cm，90%绝对误差小于0.2 cm，RNN 预测结果与BP 神经网络相比波动较平稳，预测效果更好。

对于平均绝对误差（Mean Absolute Error，MAE）指标，RNN 相比于BP 神经网络纬度减少了14.8%，经度减少了64.5%，则RNN 预测经纬度更接近真实值。对于均方根误差（Root Mean Square Error，RMSE）指标，RNN 相比于BP 神经网络纬度减少了24.8%，经度减少了60.6%，RNN 的RMSE 低于BP神经网络，预测值偏离真实值的程度得到改善，预测精度高于BP 神经网络。对于平均绝对百分比误差（Mean Absolute Percent Error，MAPE）指标，RNN相比于BP 神经网络纬度减少了13.1%，经度减少了80.7%，RNN 模型优于BP 预测模型。

RNN 相比于BP 神经网络预测经纬度更接近真实值，预测误差波动范围也更小，模型预测精度更高，基于RNN 的定位方法整体性能更佳。

3.2 不同失效时长误差分析

根据模型对比分析，选择性能更优的RNN 模型进行不同GPS 失效时长的车辆预测轨迹误差讨论。本文选取了试验中采集的4 段连续的汽车行驶轨迹，21 000 余组试验数据，分别假定GPS 失效时长为1 s、2 s、5 s、10 s、30 s，预测车辆运动轨迹。图6 为试验路径的一段，数据采集点5 800 余组。图中9 条线段分别表示车辆实际行驶轨迹和GPS 失效1 s、2 s、5 s、10 s、30 s 的预测轨迹，图7 为整体误差，图中的红色方框区域为图6 中轨迹的对应误差。

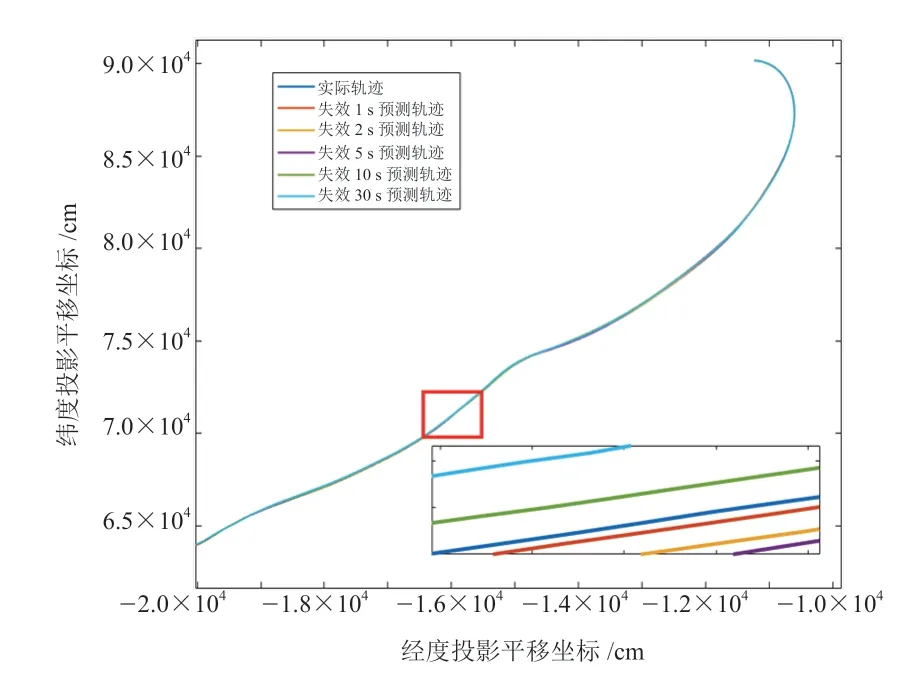
图6 不同失效时长预测轨迹对比

图7 GPS 不同失效时间整体误差分布

图6 展示了预测轨迹与实际轨迹的投影平移曲线，从局部放大图可以看出，失效1 ～2 s 短时间时，轨迹基本重合，即预测值与实际值吻合得较好，模型对测试样本有较好的预测能力，具有较强的泛化能力；随着失效时间的增加，预测轨迹偏离实际轨迹逐渐增大，偏离程度增强。

由图7 可知，随着GPS 失效时间的增加，误差随之增大，但是不是呈现比例的增大。失效时间30 s 的预测值误差最大，但均在4 m 范围内。对GPS 不同失效时长的预测数据进行细化分析，表3为不同误差范围内的数量及比例，表4 为误差指标分析。

表3 GPS 不同失效时长的误差分析

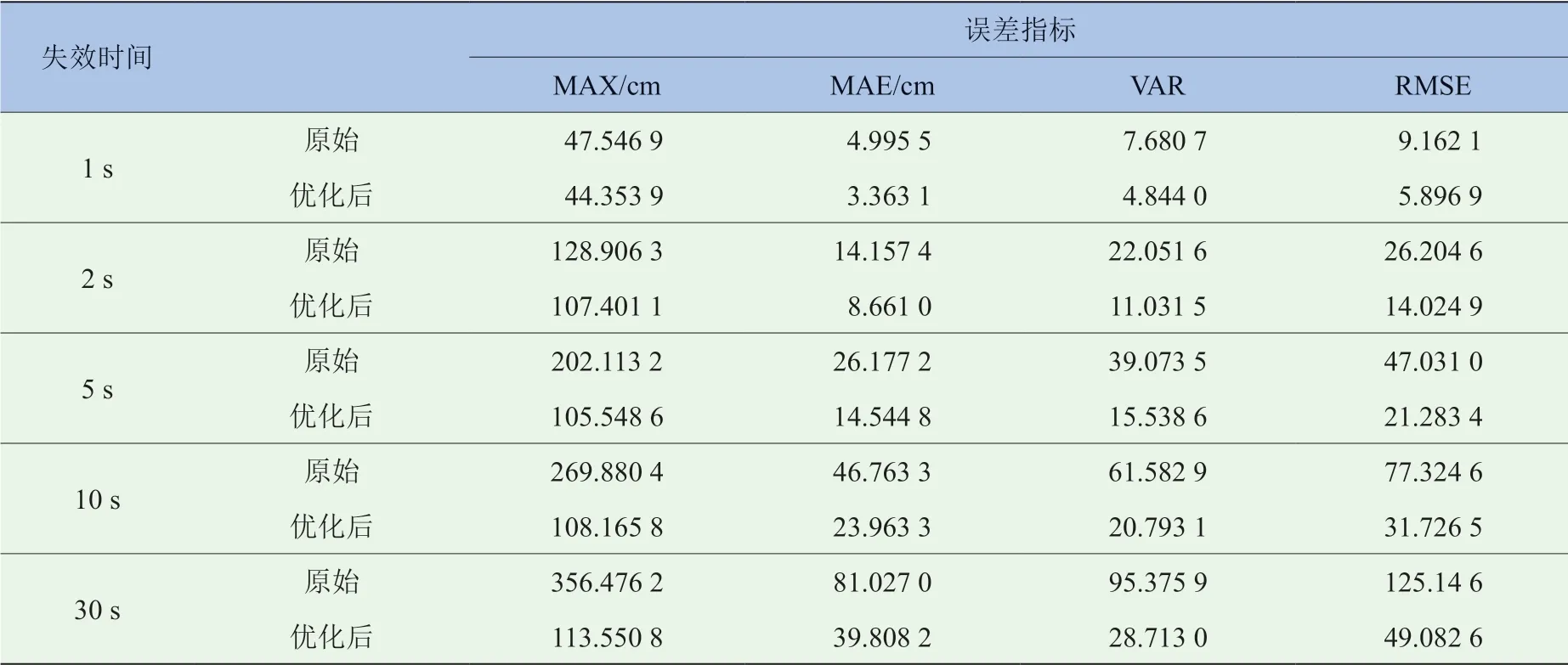
表4 GPS 不同失效时长的误差指标分析

GPS 失 效 误 差1 s、2 s、5 s、10 s 和30 s 的90%以上误差分别小于30 cm、50 cm、100 cm、200 cm 和300 cm，50%以上误差分别小于3 cm，10 cm、30 cm 和50 cm。基于RNN 的预测模型在失效30 s 内，90%的误差在300 cm 内，特别是在失效10 s 内，精度可以达到10 cm 内。随着失效时长的增加，预测精度下降，但整体预测效果良好。

对于最大值（MAX）指标，GPS 失效1 s、2 s、5 s、10 s 和30 s 分 别 约 为47 cm、129 cm、202 cm、270 cm 和356 cm，整体误差值小；平均绝对误差（MAE）分别约为5 cm、14 cm、26 cm、47 cm 和81 cm，预测值偏离真实值小，失效时间1 ～30 s 时预测精度高。对于方差（VAR）和均方根 误 差（RMSE），1 s、2 s、5 s、10 s 和30 s 的VAR 分别约为4.84、11.03、15.54、20.79、61.58 和95.38；RMSE 分别约为9.16、26.20、47.03、77.32和125.15，失效时长低于30 s 时，预测较为稳定，随着失效时长的增加，稳定性急剧下降。

在图7 中的1 200 ～1 600 条数据范围内，误差值远高于平均值，结合表4 中误差的VAR 和RMSE 偏大情况，主要是由于该时间内定位卫星数较少。此数据占总体数据的20%，去除该数据，剩余近1 700 条卫星数较多情况下的数据，表4 中优化后的数据为其误差指标分析。

对比可知，关于MAX 和MAE 指标，失效1 s时分别低于44 cm 和4 cm，比原来有少量减少；对于失 效2 s、5 s、10 s 和30 s，MAX 分别约 为107 cm、105 cm、108 cm 和113 cm，减少较多，但4 个失效时间MAX 相差较小，表明随着失效时间的增加，预测位置增量叠加增大，预测偏差程度趋于稳定。MAE 分别约为9 cm、15 cm、24 cm 和40 cm，表明预测值接近实际值，预测精度较高，随着失效时间的增加，定位精度降低。VAR 指标均低于30，RMSE 指标均低于50，表明预测波动平稳，预测系统较为稳定，但随着失效时长的增加，稳定性下降。

4 结论

本文提了一种全域GPS/INS 高精度定位方法，该方法基于GPS/INS 组合导航的定位数据，结合循环神经网络建立了一种机器学习模型。试验表明，该模型的输出结果能够高精度逼近GPS/INS 组合导航系统的定位值，在GPS 信号失效30 s 时，定位误差低于40 cm。本文提出的定位方法为组合导航系统应用中GPS 信号失锁问题的解决提供了一种有效的方法。