基于MT-BCS的可分离DOA估计算法
万连城 黑蕾 王迎斌
关键词: 二维DOA估计; 压缩感知; 贝叶斯; 多任务贝叶斯压缩感知; 分辨率; 算法复杂度
中图分类号: TN951?34 文献标识码: A 文章编号: 1004?373X(2019)06?0010?04
Abstract: The constant development of the compressed sensing theory provides a new idea for the problem of 2?D direction of arrival (DOA) estimation. The traditional 2?D DOA estimation method is only the extension of the 1?D DOA estimation, and the modeling method of the 2?D DOA estimation is the same as that of the 1?D DOA estimation, which leads to problems of high computation complexity and low resolution in solving. The multitask Bayesian compressive sensing (MT?BCS) theory is applied to the 2?D DOA estimation problem by remodeling of the 2?D DOA model, so as to propose a separable 2?D DOA estimation algorithm based on MT?BCS. A comparative experiment was carried out. The results demonstrate that the proposed algorithm has the advantages of high resolution and low complexity.
Keywords: 2?D DOA estimation; compressed sensing; Bayesian; MT?BCS; resolution; algorithm complexity
基于稀疏表示[1?3]的二维DOA(Direction of Arrival)估计算法大多是基于一维DOA估计的扩展,算法建模时也是将二维矩阵展开为向量,仿照一维DOA估计的建模方法进行建模。这类算法主要有:基于[lp]范数的POCUSS算法[2?4],经典的高分辨[lp?SVD]算法[5],MP[6],OMP[7?8]等贪婪算法和基于贝叶斯压缩感知的DOA估计算法[9]。
然而,这类仿照一维DOA的二维DOA建模方法导致稀疏基矩阵的维度过大,求解时算法的时间复杂度过高,难以满足实时性的要求。为了降低算法的时间复杂度,本文提出了可分离的二维DOA建模新方法,并使用MT?BCS(Multitask Bayesian Compressive Sensing)算法[10]进行求解,成功解决了二维DOA估计算法时间复杂度高、分辨率低的缺点。



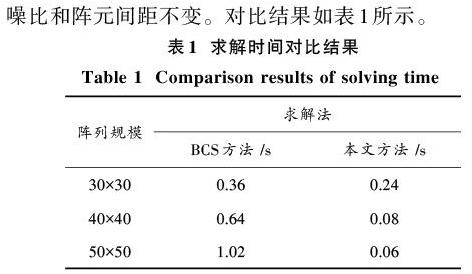
由表1可知,由于本文所提出的方法將矩阵[A∈CML×PQ] 分离为俯仰维导向矢量基矩阵[Ψ∈CM×L]和方位维[Ψ]导向矢量基矩阵[Θ∈CP×Q],从而有效地减少了算法的时间复杂度,使算法更适合工业应用。
4 结 语
对于传统二维DOA估计分辨率低、精度低、算法复杂度高等问题,本文提出基于MT?BCS算法的可分离二维DOA估计算法。该算法巧妙地将阵列流形矩阵A分解为俯仰维和方位维两个独立的低维导向矢量基矩阵,从而大大降低了算法的时间复杂度。而且算法对俯仰维、方位维进行独立估计大大提高了二维DOA估计的分辨率。由于不涉及对噪声方差的估计,算法的鲁棒性也很高。在后续工作中将进一步提高算法的分辨率,并降低其时间复杂度。
参考文献
[1] GORODNITSKY I F, GEORGE J S, RAO B D. Neuromagnetic source imaging with FOCUSS: a recursive weighted minimum norm algorithm [J]. Electroencephalography and clinical neurophysiology, 2015, 95(4): 231?251.
[2] GORODNITSKY I F, RAO B D. Sparse signal reconstruction from limited data using FOCUSS: a re?weighted minimum norm algorithm [J]. IEEE transactions on signal processing, 1997, 45(3): 600?616.
[3] GORODNITSKY I F, RAO B D, GEORGE J. Source localization in magnetoencephalography using an iterative weighted minimum norm algorithm [C]// Proceedings of the 26th Asilomar Conference on Signals, Systems & Computers. Pacific grove: IEEE, 1992: 167?171.
[4] COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors [J]. IEEE transactions on signal processing, 2005, 53(7): 2477?2488.
[5] MALIOUTOV D, ?ETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays [J]. IEEE transactions on signal processing, 2005, 53(8): 3010?3022.
[6] MALLAT S G, ZHANG Z. Matching pursuit with time?frequency dictionaries [J]. IEEE transactions on signal processing, 2013, 41(12): 3397?3415.
[7] DAVIS G, MALLAT S G, ZHANG Z. Adaptive time?frequency decompositions [J]. Optical engineering, 1994, 33(7): 2183?2191.
[8] PATI Y C, REZAIIFAR R, KRISHNAPRASAD P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition [C]// Proceedings of the 26th Asilomar Conference on Signals, Systems & Computers. Pacific grove: IEEE, 1993: 40?44.
[9] JI S, DUNSON D, CARIN L. Multitask compressive sensing [J]. IEEE transactions on signal processing, 2009, 57(1): 92?106.
[10] CARLIN M, ROCCA P, OLIVERI G, et al. Directions?of?arrival estimation through Bayesian compressive sensing strategies [J]. IEEE transactions on antennas & propagation, 2013, 61(7): 3828?3838.
[11] 刘自成.基于稀疏表示的雷达目标角度与距离估计[D].西安:西安电子科技大学,2014.
LIU Zicheng. Estimation of target′s angle and range in radar based on sparse representation [D]. Xian: Xidian University, 2014.
[12] Candès E J. Compressive sampling [C]// Proceedings of the International Congress of Mathematics. Madrid: European Mathematical Society, 2006: 1433?1452.
[13] 马文洁.贝叶斯压缩感知在DOA估计中的应用研究[D].哈尔滨:哈尔滨工业大学,2014.
MA Wenjie. DOA estimation through Bayesian compressive sensing algorithm [D]. Harbin: Harbin Institute of Technology, 2014.

