岩石蠕变效应颗粒流模拟中弹簧与黏壶参数对变形特征的影响

田佳杰，孙金山

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

岩石在应力保持不变的情况下，应变随时间延长而不断增加，发生永久变形的现象称为岩石的蠕变。岩石蠕变是岩石的重要力学特性之一，它关系到各类大型工程建设(如地基、边坡、土石坝等)、地质灾害防治(如滑坡、泥石流等)的长期安全，具有极其重要的研究价值。

对岩体流变的研究最早起源于20世纪30年代，早在1939年国外学者Griggs[1]就开展了灰岩、页岩和砂岩等岩体的蠕变试验，结果显示在这些岩体中，当荷载达到破坏荷载的12.5%～80%时，岩体就会产生蠕变现象。而自20世纪50年代以后,随着我国大型建筑工程的兴起,关于岩体流变的研究也随之引起重视，许多学者分别从室内试验、理论分析和数值模拟等方面对岩体流变力学特性展开了研究。室内试验是研究岩石蠕变的重要方法，但是工作量大、成本高。在理论研究方面，运用流变理论可以解决岩体各种黏弹性、黏塑性、黏弹塑性问题，但是如何确定各种岩体流变模型中的参数却是一个亟待解决的问题[2]。近年来，很多学者通过数值模拟的方法进行了岩石蠕变研究。如由Cundall等[3]提出的颗粒流方法及其PFC是求解非连续介质力学问题的一个重要的数值分析方法，该程序将介质离散为大量的小颗粒单元，并通过颗粒之间的相互作用去描述、研究非连续岩石材料的力学特性；Kang等[4]基于二维颗粒流程序(PFC2D)，采用法向Hertz-Mindlin模型、切向Burgers模型进行了岩石双轴蠕变试验的研究；王涛等[5]开发出广义Kelvin接触模型，并用于工程计算，结果表明与线弹性接触模型相比，采用广义Kelvin接触模型得到的结果与由Hoek-Brown强度准则得到的结果更为接近；张学朋等[6]基于颗粒流理论，采用颗粒离散元方法对微观颗粒之间的接触赋予Burgers模型，进行了二维离散元虚拟岩石单轴蠕变试验，并采用单因素法分析了颗粒粒径、摩擦因数、颗粒法向与切向刚度比对岩石流变特性模拟值的影响；孙金山等[7]采用二维颗粒流程序(PFC2D)对岩石的蠕变损伤和断裂的细观力学机制进行了数值模拟分析；胡训健等[8]基于PFC软件中的人工合成岩体技术，研究了7种不同组合形式下含断续节理岩质边坡的破坏形式及其内部微观接触力场的演变规律。

岩石蠕变效应颗粒流数值模拟中，岩石蠕变参数的选择和确定是十分困难和复杂的工作。本文基于颗粒流理论，采用颗粒流程序PFC中的Burgers模型来模拟岩石在单轴压缩状态下的蠕变试验，并采用控制变量法研究了Burgers模型中弹簧的弹性模量(Em、Ek)、黏壶的黏度系数(ηm、ηk)和摩擦因数(f)对岩石蠕变性能的影响。

1 岩石蠕变的颗粒流模拟简介

1.1 颗粒流方法简介

颗粒流(particle flow)方法是由Cundall等提出的模拟球形颗粒运动与相互作用的离散单元法[3]。这种小的球形颗粒与岩石中实际的晶体颗粒并没有什么联系，只是为了模拟岩体中的力学性质和连接状态而虚构的一种模型。岩体的力学性质可以通过颗粒间不同接触连接方式而体现出来。颗粒流方法的主要作用对象为球形颗粒和墙体，颗粒和墙体都为刚体，二维颗粒为圆盘形，球形颗粒用来组合形成岩土体本身，墙体则作为约束边界施加荷载。

1.2 Burgers模型及其参数确定

颗粒流程序(Partide Flow Code,PFC)软件中常用颗粒间的接触模型主要有接触模型、滑动模型和接触黏结模型等，但是这三种模型都不能很好地模拟出岩体的应变随时间延长而缓慢变化的性质，因此本文中将选用PFC软件中的Burgers接触模型(以下简称Burgers模型)，同时为了体现其刚度特征，还将采用线性接触模型与Burgers接触模型相串联,通过控制Burgers模型中的参数来分析岩石的蠕变性能。

Burgers模型是属于常用的元件组合模型的一种，它是由麦克斯韦(Maxwell)模型和开尔文(Kelvin)模型串联而成的，其基本原理见图1。

图1 Burgers模型示意图Fig.1 Burgers model

设Maxwell模型和Kelvin模型的应变分别为ε1、ε2，应力分别为σ1、σ2，两个模型串联后总的应变为两个应变的相加，而应力相等，故有ε=ε1+ε2,σ=σ1=σ2。

Burgers模型中细观参数是模型中两个接触部件接触点处力学性质的描述，但是在做试验时，只能观测到宏观上的变化，很难直接测得细观参数，因此需要通过建立细观参数与宏观参数之间的关系，间接地得到细观参数[5]。Burgers模型中的9个细观参数详见表1。其中,摩擦因数f为试样模型中两个颗粒之间的摩擦因数，定义为

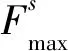
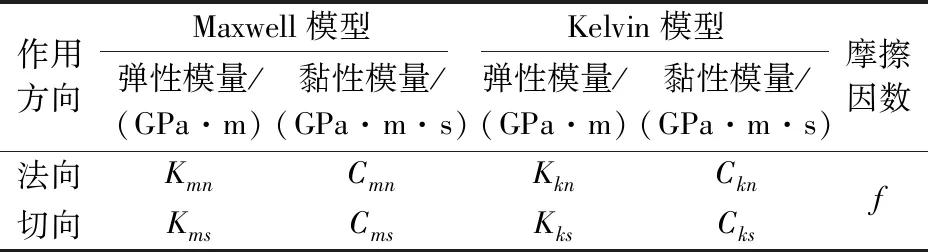
表1 Burgers模型中的细观参数

颗粒之间的接触特性与梁的两端连接2个颗粒的作用特性相同，因此颗粒之间的黏弹性特性选用两端作用一定力和力矩的黏弹性梁来描述离散单元之间的接触特性，从而推导出黏弹性宏观参数与细观参数之间的关系，其基本原理见图2[9]。

图2 黏弹性梁示意图Fig.2 Viscoelastic beam diagram

在平面问题中，设颗粒单元的厚度为h,则梁的截面面积为A=L·h[10],则可得到黏弹性宏观参数与细观参数的关系式[9]如下：

Kmn=Emh

(1)

Cmn=ηmh

(2)

Kkn=Ekh

(3)

Ckn=ηkh

(4)

根据弹性模量(E)与剪切模量(G)的关系式：

E=2(1+υ)G

(5)

可得到4个剪切细观参数如下:

(6)

(7)

(8)

(9)

上式中：L为黏弹性梁的长度，即相邻单元的球心距(m)；Em和Ek分别为Maxwell模型和Kelvin模型中弹簧单元的弹性模量(GPa)；ηm和ηk分别为Maxwell模型和Kelvin模型中黏壶单元的黏度系数(GPa·s)；υ为泊松比，取值0.25。

2 Burgers模型中细观参数对岩石变形特征的影响

Burgers模型中影响岩石蠕变的因素主要包括作用于岩石的恒定应力σ、Maxwell模型和Kelvin模型中弹簧的弹性模量Em和Ek、Maxwell模型和Kelvin模型中黏壶的黏度系数ηm和ηk以及加载时间t。

本次试验的岩石试样采用100 mm×50 mm(高×直径)的柱状模型(见图3)，模型的平均粒径设置为1.064 mm,其中最大颗粒半径为1.328 mm，最小颗粒半径为0.8 mm。对每组的每个岩石试样的顶部施加竖直向下的恒定荷载，荷载值为岩石试样单轴抗压强度的90%，即为74.4 MPa。

图3 岩石试样模型Fig.3 Sample model

针对上述参数，进行了A、B、C、D、E 5组对照试验，每组试验3次，同一组内的试验之间只变化一个参数，其余参数均取为相同，由此得到各参数对岩石蠕变特性的影响，每组对照试验参数取值见表2。

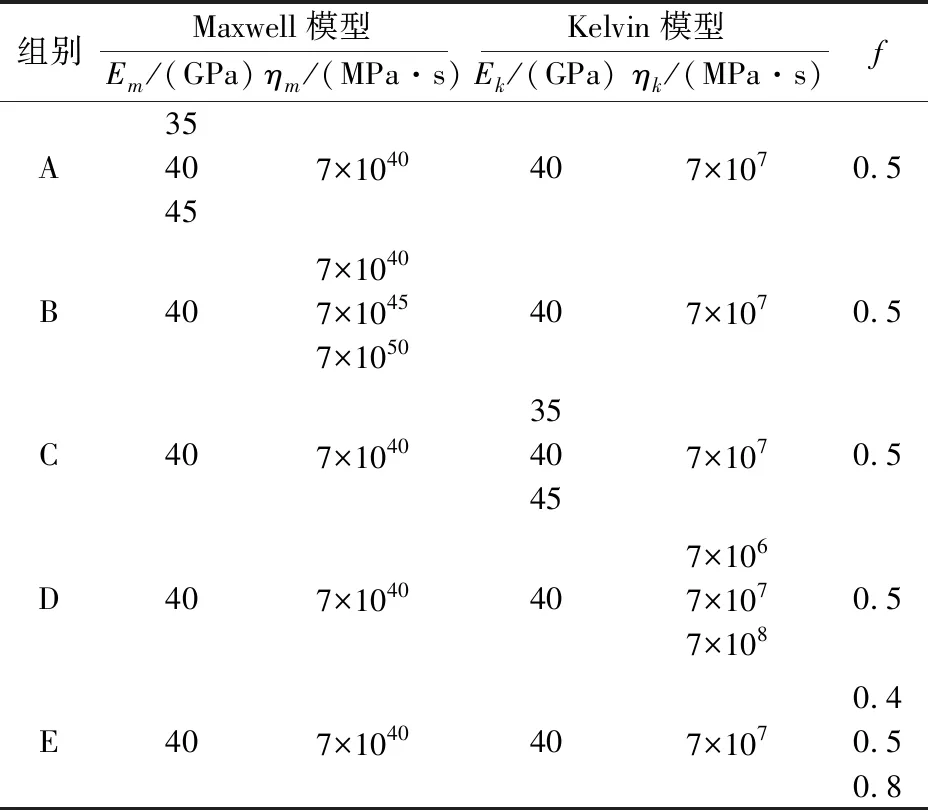
表2 对照试验参数取值

2.1 Maxwell模型中弹簧的弹性模量对岩石蠕变特性的影响

A组试验主要考虑了Maxwell模型中弹簧的弹性模量Em对岩石蠕变特性的影响。A组试验Kelvin模型中弹簧的弹性模量Ek为40 GPa、黏壶的黏度系数ηk为7×107MPa·s，Maxwell模型中黏壶的黏度系数ηm为7×1040MPa·s,摩擦因数f为0.5。

图4为Maxwell模型中弹簧的弹性模量Em分别为35 GPa、40 GPa、45 GPa所对应的岩石应变时间图像。

图4 Maxwell模型中弹簧的弹性模量Em对岩石蠕变 过程的影响Fig.4 Influence of spring elastic modulus on rock creep process in Maxwell model

由图4可见，Maxwell模型中弹簧的弹性模量Em对岩石的瞬时蠕变值影响较大，随着弹簧弹性模量的增大，岩石试样的瞬时蠕变值随之减小，其中Em值分别为40 GPa和45 GPa两种岩石试样的瞬时蠕变值相差较小；在初始蠕变阶段，Em值为35 GPa岩石试样的蠕变速率较大，该曲线上具有较明显的转折点，而进入稳定蠕变阶段以后，3种岩石试样的蠕变速率大致相同。

2.2 Maxwell模型中黏壶的黏度系数对岩石蠕变特性的影响

B组试验主要考虑了Maxwell模型中黏壶的黏度系数ηm对岩石蠕变特性的影响。B组试验Maxwell模型中弹簧的弹性模量Em为40 GPa、Kelvin模型中弹簧的弹性模量Ek为40 GPa、黏壶的黏度系数ηk为7×107MPa·s、摩擦因数f为0.5。

图5为Maxwell模型中黏壶的黏度系数ηm分别为7×1040MPa·s、7×1045MPa·s、7×1050MPa·s所对应的岩石应变时间图像。

图5 Maxwell模型中黏壶的黏度系数ηk对岩石蠕变 过程的影响Fig.5 Effect of Maxwell model viscosity on creep strain

由图5可见，当Maxwell模型中黏壶的黏度系数ηm取不同值时，3条曲线完全重合，岩石初始蠕变阶段到稳定蠕变阶段经历的时间相同，到达稳定蠕变阶段的时间也相同。由此可知，Maxwell模型中黏壶的黏度系数ηk对岩石试样的蠕变变形几乎没有影响。

2.3 Kelvin模型中弹簧的弹性模量对岩石蠕变特性的影响

C组试验主要考虑了Kelvin模型中弹簧的弹性模量Ek对岩石蠕变特性的影响。C组试验Maxwell模型中弹簧的弹性模量Em为40 GPa、黏壶的黏度系数ηm为7×1040MPa·s,Kelvin模型中黏壶的黏度系数ηk为7×107MPa·s，摩擦因数f为0.5。

图6为Kelvin模型中弹簧的弹性模量Ek分别为35 GPa、40 GPa、45 GPa所对应的岩石应变时间图像。

图6 Kelvin模型中弹簧的弹性模量Ek对岩石蠕变 过程的影响Fig.6 Influence of spring elastic modulus on rock creep process in Kelvin model

由图6可见，随着Kelvin模型中弹簧的弹性模量Ek的增大，岩石试样的瞬时蠕变值也随之增大，其中Ek值分别为40 GPa和45 GPa两种岩石试样的蠕变速率几乎相同，只有Ek值为35 GPa岩石试样在初始蠕变阶段的蠕变速率较其他两种岩石试样更大，在进入稳定蠕变阶段以后，3种岩石试样的蠕变速率则大致相同。

2.4 Kelvin模型中黏壶的黏度系数对岩石蠕变特性的影响

D组试验主要考虑了Kelvin模型中黏壶的黏度系数ηk对岩石蠕变特性的影响。D组试验Maxwell模型中弹簧的弹性模量Em为40 GPa、黏壶的黏度系数ηm为7×1040MPa·s,Kelvin模型中弹簧的弹性模量Ek为40 GPa、摩擦因数f为0.5。

图7为Kelvin模型中黏壶的黏度系数ηk分别为7×106MPa·s、7×107MPa·s、7×108MPa·s所对应的岩石应变时间图像。

图7 Kelvin模型中黏壶的黏度系数ηk对岩石蠕变 过程的影响Fig.7 Effect of viscous pot viscosity on rock creep process in Kelvin model

由图7可见，随着Kelvin模型中黏壶的黏度系数ηk的增大，岩石施加荷载时的瞬时应变值相应增大，到达稳定蠕变阶段时的应变值随之增大，其中ηk分别为7×107MPa·s和7×108MPa·s两种岩石试样的瞬时应变值相差不大；而在初始蠕变阶段岩石试样的蠕变速率却与ηk值近似呈负相关关系，即随着ηk值的增大岩石试样的蠕变速率逐渐减小。

2.5 摩擦因数对岩石蠕变特性的影响

E组试验主要考虑了摩擦因数f对岩石蠕变特性的影响。E组试验Maxwell模型中弹簧的弹性模量Em为40 GPa、黏壶的黏度系数ηm为7×1040MPa·s,Kelvin模型中弹簧的弹性模量Ek为40 GPa、黏壶的黏度系数ηk为7×107MPa·s。

图8为摩擦因数f分别为0.4、0.5、0.8所对应的岩石应变时间图像。

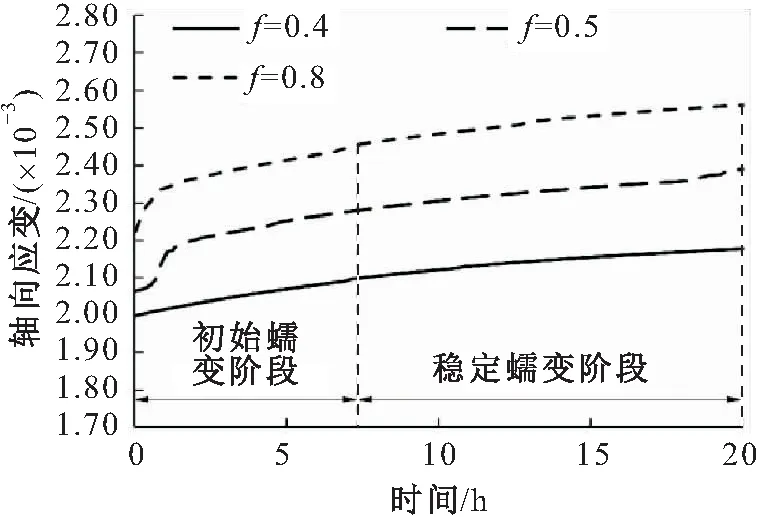
图8 摩擦因数f对岩石蠕变过程的影响Fig.8 Effect of friction factor on rock creep process

由图8可见，随着摩擦因数f的增大，岩石试样的瞬时蠕变值也随之增大；在初始蠕变阶段岩石试样的蠕变速率也随着f的增大而逐渐增大，而进入稳定蠕变阶段以后，3种岩石试样的蠕变速率大致相同。

3 结 论

针对颗粒流程序PFC中Burgers接触模型参数选择的问题，本文模拟了岩石在单轴压缩状态下的蠕变试验。模拟试验运用控制变量法，研究了Maxwell模型中弹簧的弹性模量Em、黏壶的黏度系数ηm，Kelvin模型中弹簧的弹性模量Ek、黏壶的黏度系数ηk以及摩擦因数f对岩石蠕变特性的影响,得到如下结论：

(1) Maxwell模型中黏壶的黏度系数ηm对岩石试样蠕变过程的影响不显著。

(2) Kelvin模型中黏壶的黏度系数ηk、弹簧的弹性模量Ek、摩擦因数f均对岩石试样的瞬时蠕变值有影响，且都呈正相关关系；Maxwell模型中弹簧的弹性模量Em也对岩石试样的瞬时蠕变值有影响，但呈负相关关系。

(3)ηk、Em、Ek、f都对岩石试样初始蠕变阶段的蠕变速率有影响，其中ηk、Ek、Em均与岩石试样的蠕变速率近似呈负相关关系，而f与岩石试样的蠕变速率近似呈正相关关系。