细水雾抑制受限空间原木火和纸板火的试验研究

杨 克，张 平，邢志祥，曹传先，纪 虹

(1.常州大学环境与安全工程学院，江苏 常州 213164；2.常州大学石油工程学院，江苏 常州 213106)

火灾是各类人为和自然灾害中发生频率最高的一种灾难，其危害极大，具体表现为严重威胁人类的生命安全、导致巨大的财产损失、破坏生态平衡、污染环境等[1-4]。近些年，细水雾灭火技术受到了广泛的关注，这是因为相对于其他灭火剂来说，细水雾灭火技术具有显著的优势：不会破坏臭氧层，是一种清洁无害的灭火方式；灭火时对水量的消耗较少；灭火效率较高；对火灾现场物资设备破坏性小；可扑灭某些特殊类型火灾，如动力机房、电子设备机房等[5-9]。

近年来许多学者对细水雾灭火技术的灭火效果进行了大量研究。如Liu等[10]首次对脉冲细水雾和连续细水雾的灭火效果进行了对比研究，结果发现脉冲细水雾提升了灭火效果，减少了灭火时间和用水量，可以熄灭一些连续水雾难灭的火；刘江虹等[11]研究发现细水雾主要通过冷却和稀氧窒息等物理机理灭火，它需要较高的喷射压力使得雾滴具有一定的动量，以保证其穿透火羽流到达木垛表面及其内部；姚斌等[12]对细水雾作用下池火热释放速率进行了研究，结果表明对于无水乙醇，细水雾具有较好的抑制作用；丛北华等[13-14]对细水雾抑制熄灭固体火的机理进行了研究，结果发现固体表面燃烧特性以及通量是影响细水雾扑灭固体火效率的主要因素；张笑男等[15]对机械通风条件下细水雾抑制酒精火进行了试验研究，结果表明机械通风不影响细水雾控火效果，并有助于和细水雾灭火系统共同保障火场的安全；余明高等[16]对荷电细水雾熄灭受限空间煤油火进行了试验研究，结果表明荷电细水雾能有效缩短灭火时间；周洋等[17]对不同喷射方式细水雾灭火效果进行了试验研究，结果发现细水雾对于相对密闭空间内闪点较高的可燃液体的灭火效果较好，但对于较为敞开空间内闪点较低的可燃液体，连续喷雾的灭火效果不及脉冲喷雾;Ananth等[18]对Ndubizu等人的试验进行了数值模拟，认为燃烧物的热释放速率(或反应率)伴随着火焰的熄灭有明显的下降，当燃烧物的热释放速率降低到一定临界值时，超细水雾对火焰的抑制过程也随之结束;Adiga等[19-20]对超细水雾抑制熄灭受限空间庚烷火和电缆火进行了试验研究，结果表明超细水雾是完全可以熄灭液态池火和固体电缆火的。

基于上述研究可知，大多研究采用油火或酒精为研究对象，但在实际生活中发生火灾时，火灾摧毁的大多是家具、建筑物以及固体堆积物等固体物资，它们在燃烧过程中的现象及其燃烧性能与液态火会有很大的差别，因此盲目地用细水雾扑灭液体火灾的原理来解释固体火灾显然是不合适的。为此，本文针对细水雾抑制原木火和纸板火的燃烧展开试验，通过试验获得的受限空间内不同火源温度的变化以及细水雾与不同材料火焰热成像的变化等，来揭示细水雾对于原木火和纸板火的抑燃特性，并利用均匀分析法探讨了细水雾抑制受限空间原木火和纸板火的灭火机理，分析了影响细水雾抑制原木火和纸火板的主要因素。

1 材料与方法

1.1 试验系统

本试验系统主要是由烟气分析仪、数据采集仪、受限空间、喷头、热电偶(J型)测温系统、燃烧皿、玻璃门、热成像仪构成，如图1所示。该试验系统中受限空间尺寸为1.8 m×1.8 m×3.3 m，结构为不锈钢框架，底面为瓷砖，其余5个面为钢化玻璃，正面设置一个出口(宽度为0.6 m，高度为1.8 m)以供试验时放入或取出燃烧皿；试验用喷头的末端与底面的垂直距离为3.1 m；燃烧皿为直径250 mm、高度80 mm的不锈钢圆盘，其被置于喷头正下方的底面中心处。

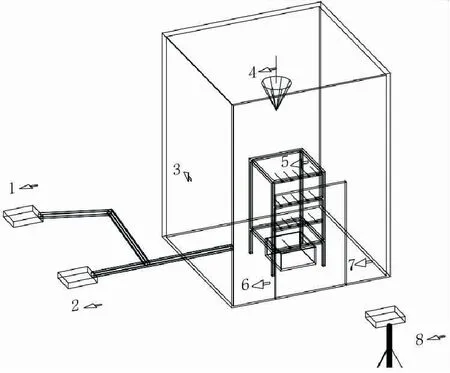
图1 试验系统示意图Fig.1 Schematic diagram of the experimental system 1.烟气分析仪；2.数据采集仪；3.受限空间；4.喷头；5.热 电偶(J型)测温系统；6.燃烧皿；7.玻璃门；8.热成像仪

1.2 试验工况

本次采用均匀分析法设计5因素8水平试验，具体详见表1和表2。

试验将50 g的纸板放在燃烧皿中燃烧，等到不同的预燃时间采用不同压力的细水雾将其扑灭。由此可见，本试验可变的关键因素为喷雾压力和预燃时间(从点火到喷淋的时间)两个因素，而这两个因素又各选定8个水平，按照从小到大的顺序对这8个水平的数据进行排列(括号内数字为对应水平的序列号)，预燃时间(s)为：20(1)、25(2)、30(3)、35(4)、40(5)、45(6)、50(7)、55 (8)；喷雾压力(MPa)为：0.6(1)、0.8(2)、1.0(3)、1.2(4)、1.4(5)、1.6(6)、1.8(7)、2.0(8)。

表1 5因素8水平均匀设计表[U8*(85)]

表2 U8*(85)的使用表

本试验采用2因素8水平的均匀试验设计方法，它属于均匀设计表 U8*(85)的使用范围，由表2可知，当因素数S=2 时，应该使用第1列和第3列，即按表1中第1列和第3列的序列号安排试验。设计时，预燃时间作为因素1，放在第1列，喷雾压力作为因素2，放在第2列，将8个水平的数据按照表1序列号在相应位置对应排列。经组合后，每一个横行都可以代表一个试验点，总共有8个试验点，详见表3。

表3 原木火和纸板火试验方案设计表

2 结果与分析

通过上述试验可得，原木火和纸板火最优组的火焰熄灭时间分别为145 s和85 s，对应的最佳水平分别为2 MPa、25 s和1.2 MPa、20 s。由于纸板与原木存在以下差异：纸板不需要引燃，原木需要酒精引燃；原木因含碳量高的缘故，其热释放速率远大于纸板。因此，本试验对比原木火和纸板火的最优灭火组，分析该两组材料的火源热成像和空间温度的变化差异，并通过计算说明原木火和纸板火的灭火效果。

2.1 原木火和纸板火的火源热成像分析

原木火和纸板火在喷淋条件下火源热成像的变化情况见图2和图3。

图2 第一组原木火在喷淋条件下火源热成像的变化图Fig.2 Thermal imaging variation diagram of the fire source of the first group of logs fires under spray conditions

图3 第二组纸板火在喷淋条件下火源热成像的变化图Fig.3 Thermal imaging variation diagram of the fire source of the second group of cardboard fires under spray conditions

由图2和图3可见，原木和纸板燃烧比较剧烈，火焰充满整个燃烧器皿，在火源表面上方的火焰形态比较连续，但是相比较而言，原木火的火焰形态要比纸板火的大，且原木的燃点要比纸板高得多，主要是因为原木含碳量大，燃烧值大；在20 s和25 s时分别开启喷淋，火焰形态在细水雾的冲击下发生了不规则变化，纸板火的火焰比较矮小，而原木火的火焰不断漂浮振荡，并伴有分叉现象；开启喷淋一段时间后，细水雾不断扼制热辐射的散播，水蒸气不断吸热同时对火源表面进行冷却，火源燃烧殆尽，喷雾压力不变，温度迅速降低直至熄灭[4-5]。

2.2 原木火和纸板火的空间温度变化分析

图4 原木火和纸板火在最佳灭火效果下的温度变化曲线Fig.4 Temperature variation chart of logs fire and cardboard fire under the optimal fire extinguishing effect

试验选择最佳水平下原木火和纸板火温度变化的两组数据曲线(见图4)进行分析，结果显示：在初始阶段，原木火和纸板火的空间温度都在上升，但是原木火的温度曲线始终处于纸板火温度曲线的上方且温度上升幅度相对较大，出现这种现象的原因：一是因为原木燃烧时的热释放速率较大，二是因为原木和纸板都是用10 mL酒精引燃且原木含碳量较高，所以在外部条件相同的情况下，原木的燃烧热值更大；在25 s和20 s这两个时刻时，原木火和纸板火的温度都分别达到了最大值43.3℃和32.2℃；在25 s和20 s时分别开启喷淋，由于细水雾在抑制原木火的过程中喷雾压力比纸板火大，所以水雾蒸发速率更快，因此原木火温度下降的速率及幅度都比纸板火要大。

2.3 灭火效果二元线性回归分析

2.3.1 二元线性回归模型

二元线性回归模型为具有一个被解释变量和两个解释变量的线性回归模型，可表示为

Yi=β0+β1X1i+β2X2i+μi(i=1,2,…,n)

(1)

对于二元线性回归模型中的偏回归系数(β1，β2)，是指多元线性回归模型中解释变量前的系数，其定义为当其余解释变量保持不变时，某一解释变量变化一个单位而使被解释变量Y同时改变的数值，即表示某一解释变量对被解释变量Y的影响程度[8]。

要估计二元线性回归模型中的参数，本文使用普通最小二乘法。假设给定一组样本数据(Yi,X1i,X2i)(i=1,2,…,n)，样本回归模型可以通过最小二乘法获得，具体表达式为

Yi=β0+β1X1i+β2X2i

(2)

(3)

(4)

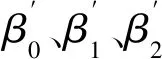
2.3.2 原木火二元线性回归模型参数估计及计算

原木火二元线性回归模型的计算参数见表4。

表4 原木火二元线性回归模型的计算参数

Y=2.946+3.32X1-1.031X2

2.3.3 纸板火二元线性回归模型的参数估计及计算

根据以上二元线性回归模型，确定以纸板火火焰熄灭时间为因变量Y，以预燃时间X1和喷雾压力X2为两个自变量，将时间单位全部转化为分钟以方便计算，具体纸板火二元线性回归模型的计算参数见表5。

表5 纸板火二元线性回归模型的计算参数

Y=1.831+1.417X1-0.469X2

2.3.4 灭火效果对比分析

原木和纸板从引燃到熄灭整个试验过程的原始数据，见表6。

表6 原木火和纸板火试验的原始数据表

注：细水雾与原木火作用时始终使用10 mL酒精作为助燃剂，且火源功率始终保持50 g。

由表6可知，原木火和纸板火试验的最优灭火工况分别为25 s、2 MPa和20 s、1.2 MPa，并且各自的火焰熄灭时间分别为145 s和85 s。原木火试验的最优灭火工况的试验数据与理论公式计算及推导的结果相一致，但纸板火最优灭火工况的试验数据与理论公式计算结果有些许出入，理论上的最优灭火工况也应与原木火一样为最大喷雾压力2 MPa时。分析原因主要是由于纸板在20～25 s时已充分燃烧，而原木在60 s之前仍处于不完全燃烧阶段，所以说次要因素预燃时间在一定条件下也会起到主导作用。在相同的条件下，细水雾扑灭原木火的时间要比纸板火相对要长，这是因为：原木的热值较大且热释放速率相对纸板较快，此外原木的含碳量较大，因此空间内温度增加相对快速；当按下喷淋按钮后，细水雾在与纸板火焰接触时受热蒸发，由于燃烧温度本身不高，但是释放的水蒸气仍然较多足以挤压氧气生存空间达到窒息效果，导致火源火焰的熄灭时间相对较短。

2.4 细水雾抑制原木火和纸板火的主要影响因素分析

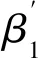
通过对均匀设计试验数据的二元线性回归分析可知，影响原木火和纸板火试验的主要因素为喷雾压力，次要因素为预燃时间，且次要因素只有在喷雾压力足够大且火源燃烧不充分的情况下才会起一定的主导作用，存在这种差异的主要原因是原木的含碳量较高，且与纸板相比更加难燃，但是一旦燃烧其热释放速率更大，在同等的外部条件下原木火自然就比纸板火所需的灭火条件更加苛刻。

2.5 细水雾抑制原木火和纸板火的灭火机理

细水雾灭火技术机理相对复杂，除了基本的窒息以及冷却两个灭火原理之外，还涉及热辐射在火场中受到削弱和阻隔、氧气等可燃气体浓度降低以及水蒸气等非可燃气体浓度不断升高的次要原理。

3 结 论

本文通过细水雾抑制受限空间原木火和纸板火的试验研究，得出以下结论：

(1) 在喷洒细水雾后，在酒精引燃的情况下，原木能够很快就进入充分燃烧阶段，因此温度急剧上升，给灭火增加了阻碍，灭火时间更长;且在外部条件相同的情况下，试验表明最佳灭火工况为最大喷雾压力为2 MPa时，这一试验结果与二元线性回归分析的理论计算结果相一致，此时所需的灭火时间最短且灭火效果更佳。

(2) 通过对均匀设计试验数据的二元线性回归分析可知，影响原木火和纸板火试验的主要因素为喷雾压力，次要因素为预燃时间，且次要因素只有在喷雾压力足够大且火源燃烧不充分的情况下才会起一定的主导作用，存在这种差异的主要原因是原木的含碳量较高，且与纸板相比更加难燃，但是一旦燃烧其热释放速率更大，在同等的外部条件下原木火比纸板火所需的灭火条件更加苛刻。