基于博弈论的风水火发电商容量优化研究*

马鸿达， 权轶, 昝皓天

(1.湖北工业大学 太阳能高效利用湖北省协同创新中心，湖北 武汉 430068;2.武汉大学 国家网络安全学院，湖北 武汉 430072)

随着节能降耗和清洁能源成为当今社会关注的热点，风电和水电在近些年来飞速发展，而目前我国为了提高大规模风电基地中风电的利用率，通常将风电与其他常规能源以联合的方式输送[1]，但在我国拥有风电、水电和火电的地区，为了更好地消纳这三种电能，一般应用打捆的方式外送.在风水火打捆直流外送系统中，送端电网的火电厂、水电厂和风电场属于不同的利益主体，彼此行为相互影响，而各方为了得到最大的利益有着竞争的关系，在竞争不当时，不仅影响电网和负荷的安全经济运行，还会影响电源建设参与者的积极性与利益以及新能源相关政策法规的制定.

电力市场其实是一个寡头市场，目前研究寡头垄断市场的理论主要是博弈论，该理论在电力市场中得到了广泛的应用，研究电力市场中发电商博弈的模型主要有Cournot、Bertrand及供应函数模型[2];其中Cournot模型是由法国经济学家Cournot在1838年建立的，在分析寡头竞争行为中起到很好的作用，该模型在发电侧的应用尤为广泛，多用于研究发电商通过改变发电出力影响市场电价并最终影响收益的情形[3-10].

为了兼顾风水火发电商各方的利益和促进新型能源的可持续发展，保证三者的良性竞争与有序发展，本文在文献[5]的基础上引入了第三方水电作为市场中的一个竞争对象，并且以三方作为标准进行容量优化的研究，这使模型的建立引入了新的约束条件，计算量增大，计算方法需要进一步地优化.

1 风水火发电容量优化

风电水电作为可再生绿色能源，为了促进其上网，《中华人民共和国可再生能源法》规定[11]，电网企业需要全额收购在其电网覆盖范围内的可再生能源，因此风、水、火电在打捆送出的时候应该优先考虑风电和水电的送出.而在一定的输电容量下，当风电、水电和火电发电的总功率超出输电容量时，火电机组则考虑降出力运行.当火电机组负荷率降低的时候，将损害火力发电商的利益，因此，在火电机组以最小技术出力运行时的风火电的总功率仍超出输电容量，则考虑风水发电商弃风弃水以使总的外送功率控制在输电容量之内.

设线路输电容量为Pl，风电场群装机容量为Pw，年持续出力特性为Pw(t)，水电厂装机容量为Ph，年持续出力特性为Ph(t)，火电机组总装机容量为Pt，最小技术出力为rPt(r为火电机组最小技术出力率)，则风水电的上网容量空间为Pl-rPt.为尽可能多地接纳风水电，应使Pw+Ph≥Pl-rPt.同时，为了维护和火电发电商的自身利益，其装机容量应该不超过线路输电容量，即Pl≤Pt.

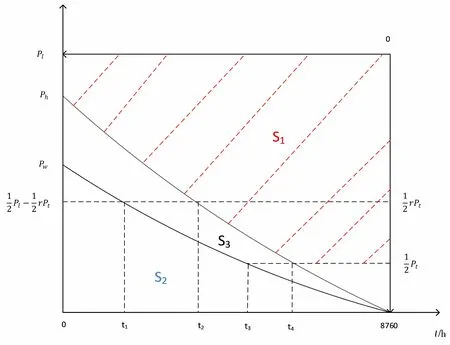
图1 输电线路年送出电量Fig.1 Annual output of transmission lines

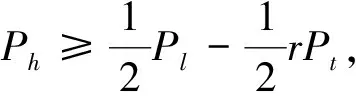
2 发电商不合作时容量优化方法

2.1 涉及三个寡头的古诺模型Nash均衡解求解

定义：在n个参与者标准式博弈G={X1，X2，…，Xn；y1，y2，…，yn}中，如果战略组合{x1*，x2*，…，xn*}满足每一个参与者i，xi*是针对其他n-1个参与者所选战略{x1*，…，xi-1*，xi*，xi+1*，…，xn*}的最优反应战略，则称战略组合{x1*，x2*，…，xn*}是该博弈的一个纳什均衡.即yi(x1*，…xi-1*，xi*，xi+1*，…，xn*)≥yi(xi*，…，xi-1*，xi，xi+1*，…，xn*).对所有Xi中xi都成立，即xi*是最优化问题

的解.

在这里，参与者为三个，设x∈[0,X]=A1,y∈[0,Y]=A2,z∈[0,Z]=A3,函数f(x，y，z)，g(x，y，z)，h(x，y，z)在A1×A2×A3上连续，且分别关于x，y，z为凹函数，求同时满足：

取得最大值的点(x,y,z).

以上所述可以看成是三寡头古诺模型的一般形式.不妨设(x*，y*，z*)是满足上述条件的最大值点，则称(x*，y*，z*)为古诺模型的Nash均衡解.

若(x*，y*，z*)是Nash均衡解，则应满足以下方程：

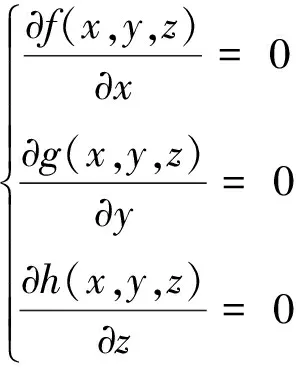
(1)

2.2 容量优化方法

综合考虑发电商的供电收益和相关设施建设成本以及维护管理成本，选取一年为周期，构建了能反映发电商利润的装机容量优化目标函数如下：

maxNj(Pw,Ph,Pt)=Rj(Pw,Ph，Pt)-Cj(Pw,Ph,Pt)-Oj(Pw,Ph,Pt)

当j=w时表示风电场，j=r时表示水电厂，j=t时表示火电厂；Nj表示发电商一年内的综合利润，Rj表示发电商年供电收益量，Cj表示发电相关设施建设成本等年值，Oj表示年运行维护成本；而供电收益量为：

Rj(Pw,Ph,Pt)=pjEj(Pw,Ph,Pt)

其中，pj为风水火电上网电价(元/MWh)；Ej(Pw,Ph,Pt)为风水火上网电量(MWh)，其计算式为：

发电相关设施建设成本等年值Cj(Pw,Ph,Pt)计算式为：

式中，cj为发电相关设施单位容量建设成本(元/MW)；ij为贴现率；nj为发电厂使用寿命(年).

年运行维护与管理成本Oj(Pt,Pa)的式子如下：

Oa(Pt,Pa)=oaPa(a=w、h)

Ot(Pt,Pa)=otPt+oeEt(Pt,Pa)+ocM(Pt,Pa)

其中，ot、oa分别为火电厂和风电场、水电厂的单位容量维护与管理成本(元/MW)；oe为火电厂单位污染物处理成本(元/MW)；oc为煤炭价格(元/t)；M(Pt,Pw,Ph)为火电厂年耗煤量(t)，另外，文献[12]提出了两种对供热机组煤耗计算公式的修正方法，得出煤耗量和发电量之间的关系：

式子中，Q为火电机组供电煤耗特性(t/MWh)，计算式为：

Q(P)=α+βP+γP2

其中，P为火电机组出力率，α,β,γ为火电机组供电煤耗特性参数.

为了求得发电商的利润最大化，现将发电商的利润函数求解一阶导，当一阶导函数值为零时，发电商的发电容量则为发电商利润最大时容量，此时，发电容量达到了最优，计算式如下：

(2)

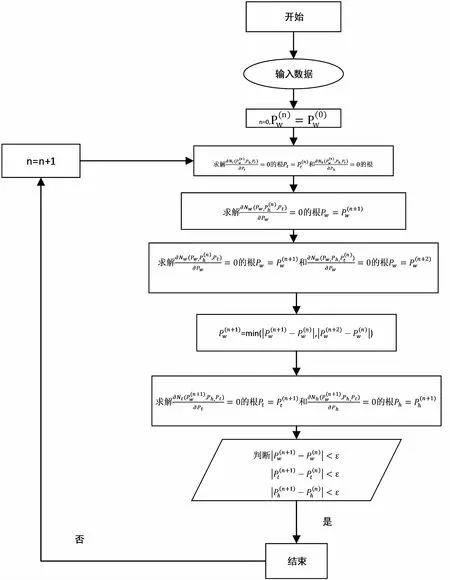
图2 发电商不合作时动态博弈过程Fig.2 Dynamic game process when generators do not cooperate

当发电商进行不合作的最优容量规划时，可以借助模型来进行博弈，图2表示给出一个风电容量的初始值,通过这个初始值求出其余两个发电商的规划容量，然后通过这两个值求出各自对应的第二个风电规划容量，通过约束条件可知为了防止计算出的第二个容量超出约束条件，因此取其最小值，然后重复以上过程，直到三方容量前后两次计算值差的绝对值小于一个很小的数ε,此时，说明三方规划容量已经趋向于一个稳定的数值，通过对比可以看出来当发电商不合作时得出来的最优均衡容量解也就是三者博弈得出的规划容量.

3 发电商合作时的容量优化方法

在这里火电与风、水电以合作的方式进行容量规划，而其最优容量规划则是当火电与风、水电发电商的利润最大的情况，目标函数如下：

max{Nt(Pt,Pw,Ph)+Nw(Pt,Pw,Ph)+Nh(Pt,Pw,Ph)}

当目标函数的一阶导数为零时，也就是当其边际利润为零时，火电与风、水电发电商的总利润为最大值，其发电容量也为最优值.即：

4 算例分析

设三方发电机组规格相同，以特高压直流线路输电为例，直流线路额定输送容量为Pl=8 000 MW.火电机组的最小技术出力为额定出力的r=50%,供电煤耗特性Q(P)=0.32 t/MWh.表1为风、水、火上网电价，表2为单位供电容量建设成本，表3为单位容量维护与管理成本.

表1 风、水、火上网电价

表2 单位供电容量建设成本

表3 单位容量维护与管理成本

此外，火电厂的污染物处理成本oe=30元/MWh,煤炭价格oc=700元/t.电厂使用寿命为nw=nh=nt=25年，贴现率为iw=ih=it=0.1.

根据以上数据及式子可得出发电商在不合作情况下的Nash均衡解只有一个，其最优规划容量为

发电商的利润见表4，发电商在合作情况下的规划容量

发电商的利润见表5.

表4 发电商不合作时最优规划容量结果

表5 发电商合作时最优规划容量结果

根据表4和表5的数据结果可以看出，发电商采取不合作策略下的风电和水电的最优装机容量比采取合作策略下的最优装机容量大，而火电的最优装机容量则相反；在利润方面，发电商采取不同策略下获得的利润中风、水电在不合作策略下的利润更高，而火电相反.这说明了在现有的可再生能源政策下，风电和水电更具有竞争性，但是，在总体利润上来看，风电和水电的竞争性使得总体利润下降.

5 总 结

风力和水力发电商在和火力发电商合作情况下的利润将会比三方自由竞争下的利润降低，而三方发电商在合作情况下的总利润则比较高，同时风力和水力的规划容量也会下降.

本文的模型、算法和结论可以为新能源电源建设各方提供决策性依据，还可为能源规划提供参考，需要说明的是，本文并未考虑风电的随机性和水电的季节性变化，针对这些不确定性因素还有待进一步的研究.