一种基于频繁项集挖掘的推荐算法

帖军，吕琴艳，孙翀，王江晴，尹帆

(中南民族大学 计算机科学学院，武汉 430074)

随着互联网和信息技术的迅猛发展，网络上的信息数据量呈指数增长，人们逐渐陷入 “信息过载”时代.在这个时代，消费者很难从众多商品中找到自己感兴趣的商品，同时生产者也很难让自己的商品在众多用户的关注中脱颖而出.推荐系统[1-3]则成为解决该问题的重要手段.它可以根据用户的喜好筛去不相关的项目，并推荐用户可能喜欢的项目.

在推荐系统中，关联规则挖掘[4]和协同过滤[5,6]是最常用和最重要的两种技术.挖掘关联规则的目的是在大型事务数据库中搜索项目集合之间的内在联系.协同过滤可以分为基于用户的推荐(User-based Recommendation)、基于物品的推荐(Item-based Recommendation)、基于模型的推荐(Model-based Recommendation)等子类.基于用户的协同过滤算法，其基本思想是先找到和目标用户有相似兴趣的用户，然后把这些用户感兴趣而目标用户没有接触过的物品推荐给目标用户；基于项目的协同过滤推荐算法，是给用户推荐那些与他们之前喜欢的物品相似的物品，主要通过分析用户的行为记录计算物品之间的相似度；基于模型的协同过滤推荐则是先使用历史数据训练得到一个模型，再用此模型进行预测.

虽然协同过滤算法取得了巨大的成功，但始终存在数据稀疏性问题.电子商务网站中用户和项目的数目非常庞大，而多数用户只会对少量的项目进行评分，导致用户之间评分的重叠部分很小，难以计算两个用户之间的相似程度.而相似性计算是基于协同过滤的推荐系统中一个非常重要的步骤.因此数据稀疏性大大降低了协同过滤的预测准确性.

基于上述分析，本文将频繁项集挖掘与协同过滤相结合，提出一种新的相似性度量方法，提高相似度计算的准确率，从而提升协同过滤算法的推荐质量.

1 相关工作

数据稀疏性[7,8]和冷启动一直是影响推荐系统的推荐性能的重要因素，针对这些问题，一些研究人员提出将数据挖掘算法与协同过滤相结合，对用户-项目评分矩阵的缺失值进行预测并填充.缺失值填补法是根据已有的用户评分数据，以某种计算方法对用户未评分的数据进行估计并填充，可以显式地解决数据稀疏问题.

Shambour等人[9]提出将来自用户社交信任网络的附加信息和项目的语义领域知识结合起来，以提高推荐的准确性和覆盖范围.Fan[10]等人提出一种基于预测值填充的UBCF推荐算法，该算法在计算用户相似度之前，通过整合基于内容的推荐算法和用户活动水平来预测用户项目矩阵中的缺失值，一定程度缓解了数据稀疏性对推荐精度的影响.Zhou等人[11]提出了一种基于SVD(奇异值分解，Singular Value Decomposition)推荐系统的增量式方法，每次迭代计算原始矩阵的奇异值分解，以解决稀疏性问题和用户兴趣的动态性.张玉芳等人[12]提出一种结合条件概率和传统协同过滤算法的非固定K近邻算法.该算法在分步填充评分矩阵思想的基础上，第一步只接受相似度和共同评分项目数量达到阈值的邻居用户作为目标用户邻居，然后计算并填充未评分项目；第二步使用第一步填充后的矩阵计算剩余未评分项目的评分.Chujai等人[13]同时使用用户信息和电影信息挖掘频繁项集，填补缺失数据.Insuwan等人[14]提出 SVDUPMedianCF 算法，该算法利用改进的K-means 算法进行聚类，得到聚类的中心来填补缺失值.刘枚莲等人[15]提出基于双向关联规则项目评分预测的推荐算法，利用双向关联规则挖掘事务数据库中相互关联的项目，找到目标项目的关联集，利用已评分项目初步预测用户对目标项目的偏好程度，从而进行推荐.

缺失值填补法可以直观、显著地改善数据稀疏问题，但其本身是对评分缺失值的一种预测，并不能真正代表用户偏好，而预测的评分对推荐结果有较大的影响，可能导致最终的推荐结果不准确.当数据十分稀疏时，使用传统的相似度计算方法往往不能得到很好的推荐效果.因此，本文提出一种结合频繁项集与协同过滤的相似度改进算法，算法考虑项目之间相互关联的特性，对项目进行频繁项集挖掘，设计一种新的相似性计算方法，对传统相似性计算方法进行改进，从而寻找项目的最近邻居并进行推荐.

2 算法设计

2.1 问题描述

协同过滤的相似度[16,17]计算只考虑用户对项目的评分数据(评分数据具有很大的稀疏性)，忽略了项目在空间上存在的相互关联性.而且，如果有恶意的评分，通过某种手段对某一特定的项目评分，并且评分很高，这无疑会带来噪声样本.这些问题都会导致推荐误差大，推荐结果不准确.如果引入事务数据库和频繁项，则可以认为频繁项是比较正常和可靠的事务数据，也可以认为频繁被用户购买的商品理论上具有较高的相似性.本文利用Apriori算法挖掘事务数据库中的频繁项集，根据频繁项集设计新的相似性度量函数，再与用户对项目的评分相似性进行加权综合，从而寻找项目的最近邻居并进行推荐.

协同过滤推荐算法是以用户-项目评分数据作为基础进行推荐的，假设U={u1,u2,…，um}和I={i1,i2,…，in}分别是用户和项目的集合，用户对项目的评分矩阵为X∈Rm×n，即矩阵X有m行n列，第i行第j列的元素Xi,j表示第i个用户对第j个项目的评分.

通过用户-项目评分数据X可以形成事务数据库矩阵D∈Rm×n，D中的每一项Di,j(i=1,2,…，m;j=1,2,…，n)表示第i个用户是否对第j个项目进行评分.具体计算方式如公式(1)：

(1)

2.2 BFIM算法

本文的BFIM算法针对基于项目的协同过滤算法，在计算项目相似度时完全依赖用户评分数据，忽略了项目在空间上的相互关联性问题，重新定义了项目相似度计算方法.算法提出对项目进行频繁项集挖掘，根据频繁项集设计一种相似性度量方法，融入到传统相似度计算方法中，然后利用该相似度更好地预测用户对项目的评分.

2.2.1 频繁项集矩阵的构建

本文采用Apriori算法进行频繁项集挖掘，根据最小支持度minSup得出全部的频繁项集.现假设对事务数据库挖掘出的频繁项集总条数为k，构建频繁项集矩阵F∈Rk×n，具体计算方法如下：

(2)

矩阵F的可能取值如表1所示.

表1 频繁项集矩阵示例Tab.1 An example of frequent itemsets matrix

由表1可知，F矩阵中{I1,I2,…，In}表示n个项目，{1,2,…,k}表示第k个频繁项集，F2,2=1表示第2条频繁项集包含项目I2，F2,1=0表示第2条频繁项集不包含项目I1.

2.2.2 相似度计算

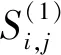
(3)

(4)

(5)

其中∂表示权重，为可调的参数.该综合相似度计算方法不仅考虑用户项目评分矩阵，同时还考虑了项目间的内在联系，二者以一定权重结合在一起，可以更准确地寻找项目的最近邻居.

2.2.3 寻找最近邻居

假设目标项目为Ia，根据相似性矩阵S筛选出所有项目与Ia的相似性值，并对其进行降序排列，选择相似性最高的K个项目作为目标项目Ia的最近邻居集合，设为Na={N1,N2,…,NK}，用户u对项目Ia的预测评分是Pu,Ia，计算方法如下：

(6)

BFIM算法以伪代码形式描述如下：

BFIM算法输入评分矩阵X∈Rm×n,目标用户u,可调参数∂,最近邻居数目K,推荐结果个数N(N<=K )输出N个推荐项目1对矩阵X筛选目标用户u未评分的项目集合Is={Is1, Is2,…, Ish};2利用Apriori算法挖掘频繁项集,构建频繁项集矩阵F∈Rk×n3根据矩阵F和公式(3)计算基于频繁项集的项目相似度矩阵S(1);4采用公式(4)计算基于用户评分数据的项目相似度矩阵S(2);5利用∂和公式(5)计算项目间的综合相似性,得到相似性矩阵S;6for i=1,2,3,…,h do7对矩阵S筛选Isi与其他项目的相似度矩阵;8根据其相似度值取Top-K个项目作为Isi的最近邻居Na;9根据公式(6)计算用户u对Isi的预测评分;10end for11对步骤6～10的结果进行降序排列,选择Top-N个项目作为用户u的推荐结果

本文算法实现中需要构建项目-项目相似度矩阵,其所需要的时间复杂度为O(n2) ，在对h个未评分项目中每一个项目进行预测时，需寻找K个最近邻居，因此本算法的时间复杂度为O(n2+h·K).

由算法伪代码可知，本文提出的BFIM算法在项目相似度计算中考虑了项目内在的关联性，对相似度计算方法进行了改进，下面将通过实验来验证算法的相关性能.

3 实验与分析

3.1 数据集

本文的实验采用目前衡量推荐系统推荐质量的最常用的MovieLens数据集(https://grouplens.org/datasets/movielens/)，该数据集是由美国Minnesota大学GroupLens研究小组公布的，它包含了943名用户对1682部电影的评分，共105条评分记录.为了进行实验比较，将数据集进行十折交叉验证，进行10次实验，每次实验将数据集的90%作为训练集，10%作为测试集.

3.2 评价指标

推荐算法的推荐效果评价标准有准确度、覆盖度、多样性等，其中准确度是推荐系统的推荐质量评估中最常用的指标，本文以平均绝对差MAE为判断算法推荐质量的标准，其计算方法如公式(7)、(8)所示.

(7)

其中，MAEu是用户u对Nu个项目预测评分的平均绝对偏差,Pu,i表示用户u对项目i的预测评分，qu,i表示用户u对项目i的实际评分，Nu是测试集所提供的用户u的评分项目数量.

(8)

其中M是全体用户总数，MAE则是测试集全体用户的平均绝对偏差.可看出，MAE的值越小，则预测越精确，算法推荐的准确性越高.

3.3 实验结果与分析

实验分为两部分，第一部分是对影响频繁项集挖掘质量的最小支持度阈值minSup和综合相似度的加权因子∂进行选取和比较，找到使算法推荐结果最优的minSup和∂.在第一部分实验取得最优的基础上，第二部分实验是对其他推荐算法与本文的BFIM算法在不同的最近邻取值下的性能进行比较，从而说明BFIM算法的有效性.

3.3.1minSup与∂选取

首先确定最小支持度minSup的大小.将∂设为0.2，minSup在0.1～0.4之间，以0.05递增，随着minSup的增加，观察算法的MAE值的变化.实验结果如图1所示.

图1 最小支持度对推荐精度的影响Fig.1 Effect of minimum support on the accuracy of the recommendation

由图1可知，将加权因子∂设为0.2时，minSup取0.2时，MAE最小，当0.2

下一步确定加权因子∂的大小.使minSup=0.2，改变加权因子∂的大小，∂∈[0,1]，每次递增0.2.实验结果如图2所示，∂=0.4时MAE值最小，因此minSup=0.2，∂=0.4，BFIM算法取得最优推荐质量.

图2 加权因子对推荐精度的影响Fig.2 Effect of weighting factors on the accuracy of the recommendation

3.3.2 算法比较

为验证本文提出的BFIM算法的性能，将基于项目的协同过滤推荐(IBCF算法)，基于项目评分预测的推荐(IRBCF算法)与本文的BFIM算法进行比较，均采用十折交叉验证法进行实验，每次随机将数据集划分为10份，选9份为训练集，1份为测试集，然后得到10次实验的验证结果.如图3所示，BFIM算法的MAE值与其他算法相比大部分都较小，即本文的BFIM算法推荐效果更好.

图3 实验次数对推荐精度的影响Fig.3 Effect of the number of experiments on the accuracy of the recommendation

图4展示了最近邻数目与MAE值的关系，最近邻数目在5～40之间，随着最近邻数目的增加，3种推荐算法的MAE值均不同程度地降低，推荐质量不断提高，当最近邻数目一定时，BFIM算法的MAE值明显小于传统推荐算法，表明文中提出的BFIM算法优于传统的推荐算法.

图4 3种算法MAE对比图Fig.4 Comparison of three algorithms on MAE

4 结语

协同过滤是如今应用成功的推荐算法之一，然而该算法过度依赖评分数据，忽略了项目间关联的特性.在数据极端稀疏的情况下，传统基于项目的协同过滤算法不能准确找到目标项目的最近邻居，导致推荐不准确.对此，文中提出的结合频繁项集与项目相似度的协同过滤推荐算法，通过Apriori算法找到事务数据库频繁被购买的项目，计算基于频繁项集的项目相似度，再与Pearson相关系数加权计算项目的综合相似度，该算法不仅考虑了事务数据的频繁项集，还考虑了用户评分数据，减小了相似度计算值与实际值的偏差，从而提高了推荐算法的质量.