密立根油滴实验在计算机统计模式下的再分析
孙继浩 朱二旷
(燕山大学理学院,河北 秦皇岛 066004)
随着密立根油滴实验仪器的不断改良,实验室测得的数据准确性相对更为精确,测量过程也更加简单.密立根油滴实验是大学里近代物理实验必做的一个项目,目前一般的数据处理方法,是对静态平衡测量法得到的数据,进行逆向验证,即用基本电荷公认值遍除各油滴带电荷量qi,得到的商值取整即为油滴所带电荷数ni,从而得到qi与ni的关系,进而计算得到基本电荷量e值.逆向验证法本身缺陷很明显,计算过程是在已知电荷的不连续性和基本电荷量的前提下进行的,主观性色彩较浓.基于以上原因,常用的逆向验证法只是简单的对数据进行处理和了解,不能验证密立根油滴实验的结论.多个文献[2-4]也提出了一些数据处理的新方案,如最小二乘法、差值法和作图法等,但仍存在着处理结果误差偏大或精度不够等缺点.
1 原理
1.1 实验原理
本文采用的测量方法是静态平衡法,求油滴带电量理论推导公式为
其中部分已知参数为:油的密度ρ=981kg/m3,重力加速度g=9.80m/s2,空气的粘滞系数η=1.83×10-5kg·m-1·s-1,油滴匀速下降的距离取l=1.2×10-3m,修正常数b=6.17×10-3m·Pa,大气压强p=1.013×105Pa,平行极板距离d=5.00×10-3m.
将已知数据代入简化后得到
由上式可知:只需要测量得到平衡电压U和下降时间tg即可求得油滴带电荷量q.
1.2 实验结果的预先分析
历史上密立根得到最终的结论是建立在大量实验基础之上的,首先他是接受了电荷量子化的思想,并用多次试验和大量数据进行验证,在此基础之上再对油滴电量的数据进行统计分析,有目的地筛选了合适的数据,这才较为精确地得到了基本电荷的数值.
本文的目的在于通过对数据本身的统计分析,首先得到电荷不连续性的结论,再对数据进一步分析,从而精确得到基本电荷数值.本文采用大量的数据进行计算机拟合,不刻意对数据进行筛选.在对数据进行分析之前,本文先对仪器测量数据的合理范围做一简单分析.
本文采用的数据为2018春季学期物理实验课程密立根油滴实验测量得到,在实验操作过程中,学生常会对油滴的带电量存在疑惑,认为油滴可能存在带有大量电荷的情况.以下将根据电量q与平衡电压U和下降时间tg的关系,及仪器的电压范围等对此进行分析.
在已知基本电荷e=1.602×10-19C前提下,平衡电压U和下落时间tg与电荷数n的关系如图1所示.选取油滴时,油滴体积大小要合适.太大的油滴下降速度过快,时间测量不准确;太小的油滴,由于布朗运动明显,速度较慢但时间测量也不准确.仪器的极板电压上限约为500V,考虑到油滴升降调节方便,初始电压一般200V左右.图1中带不同数目电荷的油滴数目不是均匀分布的,带1个电荷的油滴数量较少,带2个电荷的油滴数量较多,3个其次,带多个电荷的油滴数量逐渐变少.而实际实验过程中,油壶喷雾器喷出的油滴体积小,通过摩擦带电,一般情况下也难以带上多个电荷,这与实验数据的统计结果相符,与其他文献给出的分析类似.[5]

图1 油滴电荷数n与平衡电压U和下落时间tg的关系
2 统计分析
2.1 对实验测量数据的初步分析
本文所用数据来源于学生实验课上实际测量,共12个自然班,除去个别学生操作仪器不规范之外,其他数据未作筛选,共统计得到测量油滴1276个.
在大量数据的统计下,即便学生测量水平有差异,测量结果有偏差,如果电荷是不连续的,并存在基本电荷的话,数据应体现出一定的分布规律,即存在一些等间距的峰值.这种统计方式统计数据量越大,数据结果越可靠,与其他文献[6-7]相比本文的数据更加可靠.
根据前文公式q=f(U,tg)计算出全部1276个油滴的带电荷量,以1×10-20C的间隔统计落在各范围内的油滴数目n得到统计结果如图2所示,可以容易的看出,存在几个峰值,前6个峰值横坐标:16,33,48,64,80,97;其间距都接近16左右,那么我们可以认为这6个峰值就体现了电荷的不连续性,相邻两个峰值的差值即为基本电荷e(图中横坐标单位为10-20C).


图2 不同带电荷量的油滴数目统计图
由上述计算结果可见,第一个峰值的横坐标等于相邻峰值的差(即基本电荷量),可得出结论:前6个峰值代表的即为带电荷量分别为1~6个电荷.
与图1比较可以发现:带不同电荷数的油滴数目,基本和图1中相符合.综上所述,本文可以得出结论,根据大量数据统计,可粗略计算得到基本电荷量的计算结果如下:
E=0.02/1.60=1.3%,
E′=0.002/1.602=0.12%.(与公认值比较)
由以上结论可知,对大量数据进行统计的结果要优于用同样方法但数据量较少的统计结果[8],但如需得到更加精确的数值,还需要进一步改进方法.
2.2 利用试探电荷值进行逆向验证的极值分析
由图2我们验证了电荷的不连续性,并粗略得到了基本电荷值为(1.60±0.02) ×10-19C的结论.下面本文将结合逆向验证法的思想,通过寻找差值极小值的方法,计算分析得到较为精确的基本电荷值.
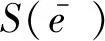
E=0.003/1.601=0.19%,
E′=0.001/1.602=0.062%.(与公认值比较)
由上述结果可知,合理采用数据分析方法,可以得到非常准确的基本电荷量的测量值,且采用的数据在测量过程中并不需要刻意筛除.

图3 试探电荷与理论e值的关系(逆向验证极值法)
3 误差分析
任何测量结果都不可避免的存在误差,前文所测量的最终结果与公认值非常接近,那么在测量和计算过程中,是否存在对结果影响较大的误差,是前文分析合理性的基础.本文结果与同类文献对比[11-12],比传统方式精度高,数据量大需要恰当方法进行处理;本文与文献[12]同样采用大数据拟合分析的结果非常接近,本文采用自测数据,参考文献使用的为大量文献的公开数据.
从计算公式可知,重力加速度g、大气压强p可能与预设参数存在差距.经公开数据查询可知秦皇岛该地区重力加速度公开数值为9.80665 m/s2,实际计算采用的g=9.80m/s2,经计算导致的误差计算约为0.034%,对应绝对误差计算可知远小于0.001×10-19C,此误差影响较小,可以忽略.所测量数据时间跨度为2月~6月,大气压强有波动,但根据公开气象数据,平均气压与采用1.013×105Pa接近,结合电荷量q计算公式,气压变化带来的误差可以忽略.测量过程中的误差主要是学生的测量准确性,由于学生接触实验时间短,操作实验仪器不够准确熟练所致.人为主观因素导致的偏差主要是随机误差,大数据下符合正态分布的特性,因此数据对结果平均值的影响可以忽略,其主要影响的是如图2所示的峰值的高度.
综上所述,本实验计算和测量两个过程存在的误差对最终结果影响可以忽略,前文计算得到的结果是合理的.
4 结论
本文对密立根油滴实验的数据进行了大数据的统计分析,通过递进式的分析验证了电荷的不连续性,并得到了较为精确的基本电荷值,同时分析了可能的误差影响.本文通过对大量数据的拟合统计,结合各种数据处理的优点,利用极值法逐渐逼近,得到电荷不连续性的结论并精确得到基本电荷的数值,在数值分析方法上和实验研究方案上有一定的指导意义.

