基于演化博弈的铁路物流外包策略研究
杨文彬
(中铁集装箱运输有限责任公司呼和浩特分公司,内蒙古 呼和浩特 010050)
1 引言
国务院在2014年印发的《物流业发展中长期规划(2014-2020年)》中明确指出:将多式联运工程列为十二大重点工程之首[1]。近年来受铁路货运改革和集装箱运输推广的影响,多式联运发展迎来了新的契机。各类扶持政策相继出台,高效、便捷的物流网络和基础设施基本建成,有效促进了多种运输方式的顺畅衔接。如何继续提升物流体系综合能力,加快多式联运运输效率,已成为影响多式联运深入发展的关键因素。A Lozano、G Storchi(2001)提出时间算法,用以解决多式联运中经营人对最优路径的选择问题[2]。Xiong,Wang(2010)设计的多任务多式联运集成模型,有效地节约了运输时间与成本[3]。F Russo,U Sansone(2014)通过对公铁联运码头周转期的某些变量进行研究,解决了公铁联运的效率问题[4]。周建勤和米晓芳(2014)指出铁路应专注于干线运输,将两端运输委托给社会物流企业,构建以铁路企业为核心的战略物流联盟[5]。孙雁胜和郝艳华(2014)探讨了铁路全程物流的两端运输,提出业务外包和构建汽运部的设想[6]。刘舰(2015)基于博弈的视角,提出了多式联运过程中分运人的选择机制[7]。崔德伟和彭永昌(2016)对物流业务外包、自营以及综合三种模式进行了分析[8]。何明珂等(2016)根据物流系统接口理论构建数学模型,为多式联运中各运输方式间的衔接选择提供参考[9]。朱汉民,姚华和刘斌(2018)从运作效率、技术效率、制度效率三方面入手,构建了集装箱多式联运效率评价指标体系[10]。当前国内外学者对多式联运的研究主要集中于效用提升和模式选择两个方面,而对多式联运企业间竞合关系的分析相对欠缺。鉴于此,本文运用演化博弈理论,通过剖析多式联运企业间竞合关系,寻求影响联运企业实现长期、稳定合作的关键因素并提出相关建议,以期为我国铁路物流深入发展提供参考。
2 铁路物流企业与外包车队博弈关系分析
2.1 合作关系分析
(1)合作动因。一是具备优势互补。铁路运输网络遍及我国各大、中型城市,运量大、成本低、安全、环保等优势弥补了汽运的不足;公路运输则以其机动性好、灵活性强等优势弥补当前铁路两端运输的缺失。二是实现资源共享。铁路物流企业可凭借外包车队的设施、网点以及丰富的市场经验有效组织两端运输;外包车队则通过接受铁路物流企业下达的订单,获取稳定货源和物流收入。
(2)合作形式。目前我国铁路物流企业与外包车队主要采用契约式的合作形式,该种合作形式是双方签订物流外包合同,并在后期执行过程中严格依照合同内容组织运输。
2.2 不合作关系分析
(1)不合作的动因。一是拓展市场份额。近年来由于物流市场蓬勃发展,不少商家都看到其光明的前景,越来越多的企业进入市场参与竞争。想要在竞争激烈的物流市场中谋取进一步发展,拓展市场份额是必不可少的。二是获取更多收益。收益不仅指企业所获得的经济指标,还包括企业名誉、技术水平、管理经验等指标。当合作企业认为在合作情况下取得的收益会少于不合作情况下取得的收益,往往倾向于不合作。
(2)不合作的形式。不合作的形式有两种:一是相互竞争,二是互不影响,独立经营。其中竞争又分为恶性和良性竞争两种形式。恶性竞争形式是价格战,为战胜对方,竞争企业间会不计后果的降低产品价格,直至把对手挤出市场。良性竞争形式是技术创新,通过研发全新的物流技术或设备提升竞争力,但此种竞争方式回报周期较长。
3 演化博弈模型构建
3.1 问题描述与模型假设
(1)假设铁路物流企业在开展业务外包的过程中存在以下博弈主体:铁路物流企业、外包车队。其中,外包车队负责组织两端“门到站”和“站到门”的公路运输,铁路物流企业负责组织铁路干线运输并协调外包车队的接取送达工作。
(2)假设:(a)有限理性。博弈各方都追求自身利益最大化,但由于自身因素的限制几乎无法一次性选择到最优策略。(b)存在演化博弈行为。在开展业务外包的过程中,博弈主体均存在演化博弈行为。
(3)博弈策略集合:在物流业务外包过程中,铁路物流企业可选择“合作”与“不合作”两种策略;同样,外包车队选择的策略也可能是“合作”、“不合作”。
(4)根据演化博弈问题描述,将有关参数做如下定义,见表1。

表1 变量及解释
3.2 模型构建
依据问题描述与模型假设,建构铁路物流企业与外包车队收益矩阵,见表2。
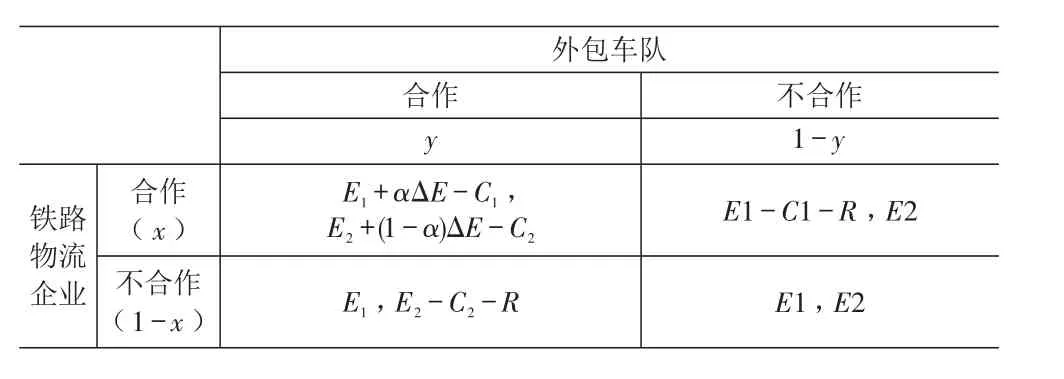
表2 铁路物流企业与外包车队收益矩阵
铁路物流企业选择“合作”策略的期望收益为:
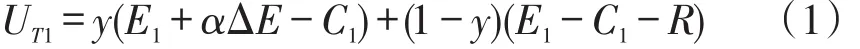
铁路物流企业选择“不合作”策略的期望收益为:

铁路物流企业的平均期望收益为:
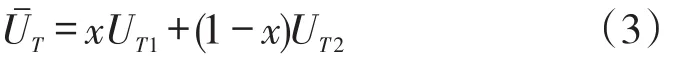
铁路物流企业的复制动态方程为:

同理,外包车队的复制动态方程为:

4 模型稳定性分析
根据上述内容,得到铁路物流企业与外包车队的雅可比矩阵:

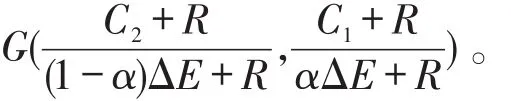
根据定理可知,只有当所列均衡点行列式的值大于0,同时满足它的迹小于0时,系统在该点处才能实现演化稳定的状态。
(1) 当 αΔE<C1, (1-α)ΔE<C2时 ,故点G不在系统内,该系统中的均衡点分别为 A(0,0),B(0,1),C(1,0),D(1,1)。对上述四个均衡点做局部稳定性分析,见表3和图1。

表3 局部稳定性分析

图1 系统演化相位图
在开展物流业务外包过程中,铁路物流企业获得的超额收益无法弥补其投入的成本,同时外包车队获得的超额收益也无法弥补其投入的成本。此种情况下,合作过程中双方均未获得收益。系统演化结果最终将趋于点A(0,0),即铁路物流企业和外包车队均会选择不合作策略。
(2)当 αΔE>C1,(1-α)ΔE<C2时故点G不在系统内,该系统中的均衡点分别为 A(0,0),B(0,1),C(1,0),D(1,1)。对上述四个均衡点做局部稳定性分析,见表4和图2。

表4 局部稳定性分析

图2 系统演化相位图
在开展物流业务外包过程中,铁路物流企业获得的超额收益大于其投入的成本,同时外包车队获得的超额收益无法弥补其投入的成本。此种情况下,虽然在合作过程中铁路物流企业获得了收益,但外包车队却未获得收益,甚至可能出现亏损。系统演化结果最终将趋于点A(0,0),即铁路物流企业和外包车队均会选择不合作策略。
(3)当 αΔE<C1(1-α)ΔE>C2时 ,故点G不在系统内,该系统中的均衡点分别为 A(0,0),B(0,1),C(1,0),D(1,1)。对上述四个均衡点做局部稳定性分析,见表5和图3。

表5 局部稳定性分析
在开展物流业务外包过程中,铁路物流企业获得的超额收益无法弥补其投入的成本,同时外包车队获得的超额收益大于其投入的成本。此种情况下,虽然在合作过程中外包车队获得了收益,但铁路物流企业却未获得收益,甚至可能出现亏损。系统演化结果最终将会趋于点A(0,0),即铁路物流企业和外包车队均会选择不合作策略。

图3 系统演化相位图


表6 局部稳定性分析

图4 系统演化相位图
在开展物流业务外包过程中,铁路物流企业获得的超额收益大于其投入的成本,同时外包车队获得的超额收益也大于其投入的成本。此种情况下,铁路物流企业和外包车队会实现合作。但合作过程中G点位置改变,会影响双方的合作结果。当G点位于折线BGC上方时,双方最终会趋于合作;当G点位于折线BGC下方时,双方最终会趋于不合作。
5 数值仿真验证
借助MATLAB软件运用数值仿真的方法,对上述推论作进一步研究。数值仿真图中横轴表示时间t,纵轴表示概率 p。
5.1 初始合作意愿
当ΔE=10,C1=3,C2=2,R=1,α=0.6,初始合作意愿分别为以下两组值时,系统演化结果如图5、图6所示。
数值组1:x=0.73;y=0.82;
数值组2:x=0.41;y=0.53。
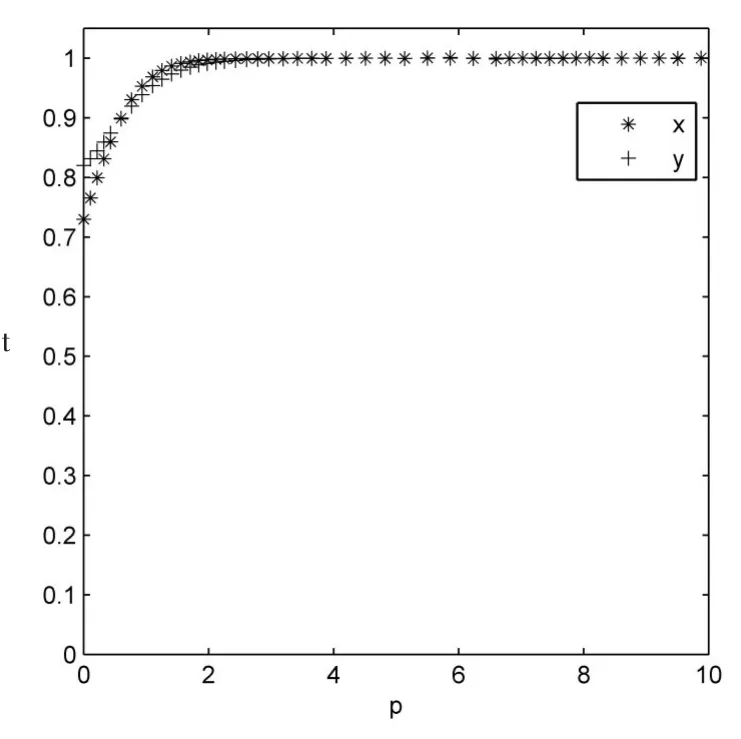
图5 初始合作意愿数值组1仿真
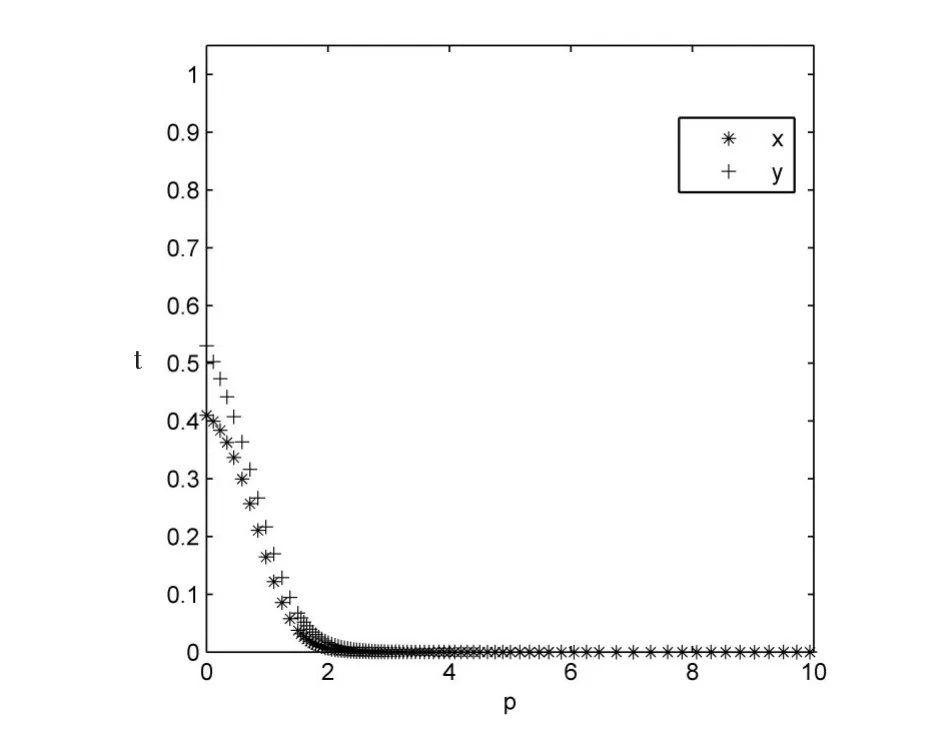
图6 初始合作意愿数值组2仿真
从图5、图6可以发现,当初始合作意愿变化时,双方合作结果会发生改变。在上述条件下点G的坐标为(0.6,0.57)。当铁路物流企业与外包车队的初始合作意愿处于折线BGC的右上方时,双方最终趋于合作;当铁路物流企业与外包车队的初始合作意愿处于折线BGC的左下方时,双方最终趋于不合作。
5.2 超额收益
当 C1=3,C2=2,R=1,α=0.6,x=0.41,y=0.53,超额收益分别取以下两组值时,系统演化结果如图7、图8所示。
数值1:ΔE=10;
数值2:ΔE=15。
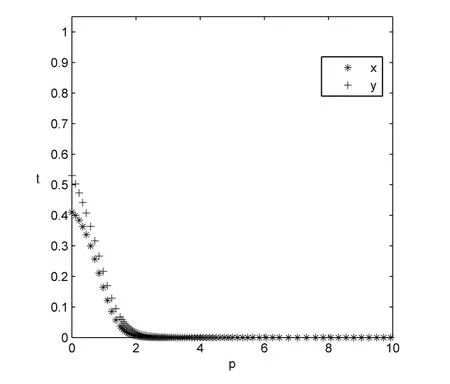
图7 超额收益数值1仿真

图8 超额收益数值2仿真
从图7、图8可以发现,当超额收益变化时,双方合作结果会发生改变。在其他条件不变的情况下,铁路物流企业和外包车队获得的超额收益越高,双方越趋于合作。
5.3 超额收益分配系数
当 ΔE=10,C1=3,C2=2,R=1,x=0.73,y=0.82,超额收益分配系数分别取以下两组值,系统演化结果如图9、图10所示。
数值1:α=0.7;
数值2:α=0.6。

图9 分配系数数值1仿真

图10 分配系数数值2仿真
从图9、图10可以发现,当超额收益分配系数变化时,会加速双方的合作结果。在其他条件不变的情况下,外包车队超额收益分配系数越大,双方实现合作的速度就越快。
5.4 企业投入成本
当ΔE=10,R=1,α=0.6,x=0.73,y=0.82,企业投入的成本分别取以下两组值时,系统演化结果如图11、图12所示。
数值组1:C1=3,C2=2;
数值组2:C1=6,C2=4。

图11 企业投入成本数值组1仿真

图12 企业投入成本数值组2仿真
从图11、图12可以发现,当企业投入成本变化时,双方合作结果会发生改变。在其他条件不变的情况下,铁路物流企业和外包车队投入的成本越低,双方越趋于合作。
5.5 风险成本
当 ΔE=10,C1=3,C2=2,α=0.6,x=0.73,y=0.82,风险成本分别取以下两组值时,系统演化结果如图13、图14所示。
数值1:R=1
数值2:R=8。

图13 风险成本数值1仿真

图14 风险成本数值2仿真
从图13、图14可以发现,当风险成本变化时,双方合作结果会发生改变。在其他条件不变的情况下,铁路物流企业和外包车队认知到的风险成本越小,双方越趋于合作。
6 结论
在对铁路物流企业和外包车队博弈关系分析的基础上,从业务外包出发,运用演化博弈理论,构建了两两博弈的数学模型,指明了铁路物流企业和外包车队的策略选择,主要结论如下:
(1)解决了铁路物流企业与外包车队合作共生发展没有基于动态演化与有限理性视角考虑经济收益与成本投入等影响的不足,指明了铁路物流企业与外包车队能够协同发展的存在基础。
(2)一方甚至双方收益均受损时,铁路物流企业与外包车队出于自身利益考虑最终会趋于不合作;双方超额收益均大于其投入成本时,铁路物流企业与外包车队最终是否趋于合作,受初始状态和关键参数的影响。
(3)铁路物流企业和外包车队合作与否受初始合作意愿影响,会随双方超额收益和超额收益的分配系数增加而增大,随双方投入成本和风险成本的增加而减小。为了使铁路物流企业和外包车队能够实现长期、稳定的合作,应该尽量创造超额收益并实现合理分配,合理安排运输计划降低投入成本,最大限度地减少风险成本的产生。

