沉管隧道加测陀螺边的地下导线贯通误差预计模拟法研究
马 骥,石 震,张学伟
(长安大学,陕西 西安 710054)
在进行贯通测量前,通常需要对地下导线进行贯通误差预计[1-2]。传统的贯通误差预计方法(图解法或解析法)需要人工量取设计图纸,效率低下。随着计算机技术的发展,一些学者基于不同的编程平台实现了误差预计功能,提高了误差预计的效率[3-4]。大量的工程实践表明,由于解析法没有考虑随机误差之间所存有的相互抵偿性,使得贯通误差预计的结果偏保守。文献[5]提出利用计算机生成的随机数构成模拟观测值,采用导线平差方法计算贯通点偏差的模拟贯通误差预计方法。武汉大学开发的COSA软件包实现了模拟观测网平差功能[6]。文献[7—9]结合目前特长隧道施工特点将模拟仿真数据用于超长隧道的贯通误差预计中。
在地下导线网中加测陀螺边是提高地下平面控制网精度的有效方法,对于加测陀螺边的地下导线贯通误差预计,目前大多数工程仍沿用文献[10]提出的视陀螺边为坚强边,按附合导线分段重心求估值的解析法。该方法适用于简单的支导线,对于复杂的导线网型,简化后的公式无法准确表达。在进行贯通误差预计时有必要将陀螺观测值的随机误差抵偿性、陀螺仪器常数误差等因素考虑在内[11]。本文基于蒙特卡洛(Monte Carlo)基本原理,顾及陀螺定向测量的观测方式和误差分布规律,利用计算机生成的模拟观测值代替陀螺观测值进行贯通误差预计,并以港珠澳大桥沉管隧道1∶1实景模拟试验[12],验证该方法的可行性与可靠性。
1 蒙特卡洛模拟法贯通误差预计原理
蒙特卡洛方法也称随机模拟(random simulation)方法。观测误差中包含偶然误差和系统误差。系统误差可以究其原因而设法改正。对于偶然误差,可利用计算机生成一系列服从误差分布规律的随机数,将这些随机数进行数学变换后与相应的理论值相加,使其与观测误差基本相符,就可得到一系列被扭曲的模拟观测值。
1.1 生成正态分布的伪随机数
根据中心极限定理,大多数观测误差服从正态分布。利用计算机随机数发生器,生成一组在区间(0,1)上均匀分布的伪随机数序列{ri}。经过均匀性和相关性检验后,根据文献[13]提到的变换法,变换为服从标准正态分布的随机数
(1)


(2)
式中,μ为模拟观测值中的理论值(设计值);σ2为观测值的精度,对于边长观测值可取全站仪标称测边精度,水平角观测值取全站仪标称测角精度,陀螺观测值取陀螺仪标称定向精度。
1.2 伪随机数的正态分布检验
针对沉管隧道工程应用中陀螺观测数量较少的实际情况,在小样本容量(n<50)下,总体服从正态分布的假设不成立,相应的参数检验失效,统计推断不可信。因此采用Kolmogrov-Smirnov法(K-S检验)进行正态分布检验[14]。将随机数列{xi}从小到大排序后x(1),x(2),…,x(n),记经验分布函数为Fn(x);将Fn(x)与正态分布函数F(x)相比较,其最大偏差即为K-S检验统计量
(3)

1.3 陀螺方位角观测值的模拟
通过正态分布检验的伪随机数即可视为模拟观测值,对于陀螺观测值而言,伪随机数进行的是一次定向观测值的模拟,如图1所示,若要模拟最终需要的陀螺坐标方位角αCD还需要进一步计算。
(4)

(5)
式中,mT0为陀螺一次定向中误差,可取仪器的验前标称精度。
2 基于模拟观测值的贯通误差预计
用模拟法估算隧道横向贯通误差,可采用以下几种方式。
2.1 误差椭圆法
在生成各类模拟观测值后,按照导线间接平差方法求各导线点的坐标平差值,再由参数的协因数阵计算各点位误差椭圆的元素,在垂直于贯通面方向上作椭圆的切线,垂足与原点的连线长度即为贯通重要方向上的位差。特别的,若贯通面与坐标Y轴垂直,则导线点在贯通重要方向上的位差即为误差椭圆长半轴E。
(6)
式中,σ0为单位权中误差;Qxx、Qyy为X和Y的协因数阵;Qxy为X关于Y的互协因数阵。顾及进口导线与出口导线贯通点的横向点位误差相互独立的共同影响,则综合横向贯通误差影响值为

(7)
2.2 坐标差统计法
假设贯通面与X轴平行,分别计算进、出口导线同一贯通点的X、Y坐标,其X坐标差即为洞内导线测量误差所引起的横向贯通误差。若模拟计算了n次,横向贯通误差预计值可按下式计算

(8)
式中,Δxi为同一贯通点进口导线和出口导线X坐标差。
2.3 坐标中误差法
假设贯通面与X轴平行,生成多组模拟观测值,对进、出口导线分别平差,可得到多组贯通点的X、Y坐标,分别计算其中误差,则横向贯通误差预计值可按下式计算
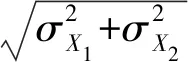
(9)
式中,σX1、σX2分别为进、出洞导线贯通点X坐标中误差。
3 港珠澳大桥沉管隧道贯通误差预计模拟法
3.1 工程概况
港珠澳大桥岛隧工程全长约7440 m,在海底埋深超过20 m建设长达5664 m,共计33节管节的沉管隧道,在全世界尚属首次[15]。由于沉管隧道管节沉放控制标准精度要求高,为保证隧道新沉管节和已沉放管节的安全对接,试验组选取与工程条件相近的城市道路开展实景模拟试验工作。按照1∶1比例,布设GPS网和全导线网,加测陀螺边,验证测量方案的可行性。
在试验区域左、右行车道分别布设全导线网,贯通点为RN29-1;分别将各导线点在隧道左、右行车道中轴线两侧3.5 m左右位置对称排列。东人工岛方向受曲线段影响导线边长控制约180 m左右,西人工岛方向导线边长约720 m。如图2所示,在左、右行车道分别加测3条陀螺边,共6条陀螺边。导线测量采用LeicaTS30全站仪,标称测角精度为0.5″(误差预计时,将测角先验精度放大至1″),标称测距精度为0.6 mm+1×10-6D,选用德国DMT公司生产的G3000陀螺仪(标称精度3″)进行定向测量。地面仪器常数边独立测定6测回,地下待定边独立测定2测回,则根据式(5)可求得陀螺坐标方位角的模拟中误差为2.5″。
3.2 试验结果
根据设计坐标与先验精度指标生成一系列伪随机数,构成导线边长、导线转折角及陀螺方位角模拟观测值,共生成50组相互独立的模拟观测值,每组包含6个陀螺模拟观测值和500个相互独立并且通过正态分布检验的伪随机数。模拟值变化区间及其中误差见表1。
采用解析法与上述3种模拟方法进行横向贯通误差的计算和比对。用COSA软件对不同样本容量下的每组模拟观测值分别进行平差,求得各导线点平差值,绘制误差椭圆,计算贯通点RN29-1的横向贯通误差预计值。在样本容量为1的条件下,随机选取了5组单次模拟计算的贯通误差,其结果见表2。

表2 单次模拟贯通误差预计结果比对
由表2可知,解析法与误差椭圆法的结果不随模拟观测值的不同而变化,这是由于解析法是根据设计导线网的几何关系按照既定的先验精度指标推估导线点可能出现的最大误差,模拟观测值的变化对其没有影响;而误差椭圆法是按照模拟观测值先验精度定权,列误差方程,根据误差传播定律求协方差阵计算导线点位误差,不同样本间模拟观测值的差异对预计结果影响不大。对坐标差统计法而言,不同的样本模拟观测值的随机性差异对预计结果影响很大,存在明显的偶然性;而坐标中误差法由于只有单次模拟的结果,而无法计算相应的统计量。因此采用单次模拟(样本容量为1)的结果作为预计值是不可靠的。为了研究不同样本容量下各类预计方法的效果,现对不同模拟次数下的各类预计方法进行比对,结果如图3所示。
由图3可知,解析法相对保守,其预计值大于其他3种方法。误差椭圆法与坐标中误差法预计结果接近,而且大于坐标差统计法。与之不同的是,坐标差统计法和坐标中误差法的预计结果受模拟观测值的偶然性影响较大,但随着样本容量的不断增加,坐标差统计法与坐标中误差法的预计结果逐渐收敛于一个平稳的区间。坐标差统计法虽然比坐标中误差法的预计结果小,但变化范围较大,这是由于偶然误差的影响,进口导线贯通点在贯通面上的偏移方向和出口导线对应点的偏移方向可能相互抵消,也可能相互叠加。而坐标中误差法将进口导线和出口导线的坐标中误差进行了综合,顾及了贯通点在贯通面方向上偏移的可能性。但是坐标差统计法的预计值的中误差量级(图3中误差棒所示)与坐标中误差法的预计值大小基本一致。
4 结论与讨论
2015年9月,试验组完成1∶1模拟试验网导线测量与陀螺定向测量,实测贯通点RN29-1的贯通误差为-6.6 mm,小于贯通误差预计值。按照与模拟试验相似的测量方案在港珠澳沉管隧道现场进行贯通测量,2017年5月,沉管隧道实现顺利贯通,贯通精度为12 mm(限差±25 mm),验证了该测量方案的可行性和可靠性。
由上述试验结果可得出以下结论:①解析法预计结果远大于实测贯通误差,该方法没有考虑随机误差的抵偿作用,因此贯通误差预计结果偏于保守。②由误差理论可知,绝对值相等的正负随机误差出现的概率是相近的,在随机过程中,偶然误差对其函数的影响是可以相互抵偿的,因此模拟法预计结果更接近实测贯通误差。③由于偶然误差的存在,单次模拟的预计结果不可靠。随着模拟观测值样本容量的不断增加,模拟计算得到的横向贯通误差预计值的均值趋于稳定,预计值的中误差也逐渐平稳。对于本次试验而言,模拟了50组观测值,可达到较好的效果。
需要注意的是,试验中假定生成的模拟观测值是服从正态分布的,但实际观测过程中,由于人为误差、工作环境等影响因素,导致观测误差的分布可能是非正态的。若继续使用服从正态分布的模拟观测值进行贯通误差预计,有可能使得预计结果小于实测贯通误差,增加了方案实施的风险。尽管解析法的预计结果比较保守,但其数学理论推导过程是严密的,它给出了误差可能会出现的阈值范围。因此在进行贯通误差预计时可考虑:①适当地放大观测误差先验指标;②按照特定的系统误差分布规律生成相应的非正态模拟观测值;③人为地在模拟观测值中摄入一定量的粗差;④模拟法与解析法同时进行,误差预计结果相互校核,若观测过程符合规范要求,贯通实际偏差应小于解析法预计结果,并与模拟法的误差预计结果较为接近,这两种方法的结合可实现优势互补,可以提高误差预计的可靠性,做到贯通测量心中有数。

