密码风云 “谜”与“如谜的解谜者”（七）

花卷

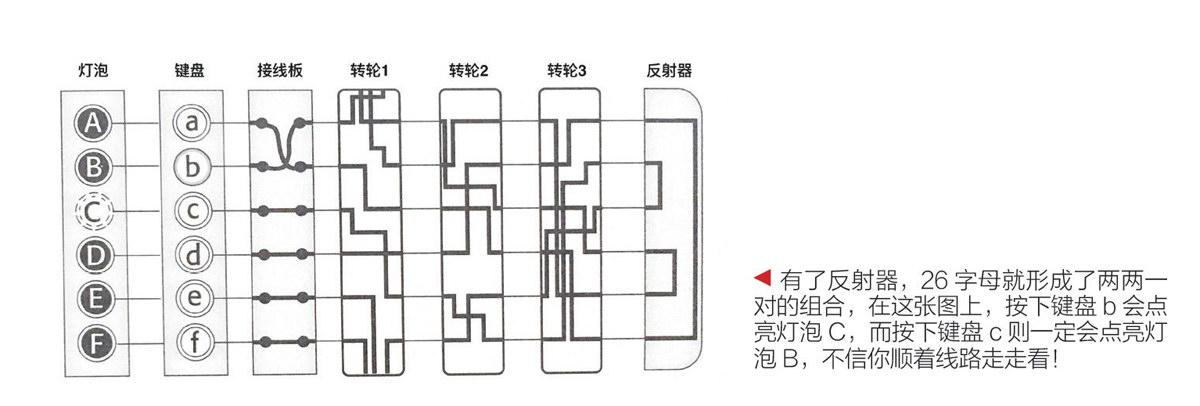
尽管Enigma密码机在设计上提供了划时代的加密强度，但是在实际运用中还是会遇到密钥配送问题。为了解决这个问题，德军采用了“每日密码本”加上“指标组”的组合，即把一个月中每一天的转轮顺序和初始位置印成密码本人工分发到每个部队的通讯员手中，然后对于每一封电报，通讯员需要自行设置一个3个字母长度的“指标组”并重复两次，用每日密钥进行加密后发出。这一操作方法实际上在安全性上做出了妥协，也成了日后破译Enigma的重要突破口。

天降大任

1932年9月1日，波兰华沙。三位波兹南大学数学系硕士——雷耶夫斯基、齐加尔斯基和鲁日茨基，正式来到波兰密码局总部报到。第一天上班大家还都只是干点普通的工作，好像也没什么特别玄乎的任务，但是密码局似乎很快就发现这位小雷同学有点不一般，毕竟学霸的光芒是想藏也藏不住的呢。于是，过了没多久，小雷同学就被调到了一个单独的房间。小雷心想，这是啥情况？在独立办公室办公，这不是老板的待遇么？难道我这么快就升官了？

小雷当然不是去当老板了，等待他的可是一块烫手的山芋——Enigma。正如我们前面讲过的，密码局之前也尝试过破译用Enigma加密的密电，但却一点办法都找不到，就在这时小雷他们三位数学专家加入了密码局，这可真是雪中送暖宝宝啊。特别是小雷，听说在密码课程中成绩相当不错，让这种学霸破译那些不入流的密码，还不如给他个有点挑战性的玩意儿试试看。于是，小雷刚加入密码局不久，就被抓去破译Enigma了，而且这是一项机密任务，小雷必须单独關在一个秘密的房间里工作，还不能跟其他们任何人透露他究竟在干什么——对，就连跟他一起进来的两个好基友也不能说！

几个前辈都搞不出来的Enigma居然落到自己头上，小雷感觉这个工作压力山大，而且他手上也没有太多的资料可以参考，他的秘密办公室里只有密码局从正规渠道买来的一台商用版Enigma密码机，以及每天截获的用Enigma加密的密电文。还记得我们讲过的商用版Enigma和军用版的区别么？它们主要的区别就是转轮内部的接线方式不一样，而且商用版Enigma不带连接板。我们知道，转轮的接线方式是Enigma的三个秘密之一，显然，商用版的转轮怎么接的拆开看看就知道了，但是军用版的跟它完全不一样啊！那是不是说，研究这台商用版的机器就一点用都没有了呢？

当然不是，这台商用版的机器，除了转轮接线方式和连接板之外，其他的部分——比如加密解密的基本原理、转轮的步进方式以及反射器的设计——这些都跟军用版是一模一样的，也就是说，通过研究和分析这台商用版Enigma，小雷就可以搞清楚它的工作原理，并且还可以把它的加密方式写成数学公式，然后再分析公式中哪些是已知的，哪些是未知的——你看，数学家的思路就是跟一般人不一样！

指标组的暗示

那么小雷通过这些分析，到底发现了什么玄机呢？他发现的第一个突破口，就在这个指标组身上。我们之前说过，指标组是一个“妥协”的产物，而且指标组在发报时要放在电文开头，还需要重复两次，这对于破译者来说是一个非常重要的线索——现在这个线索被小雷抓住了！

可是，这个线索有什么用呢？别急，我们慢慢来分析。还是回到上次的例子（如果不记得的话，再回顾一下上一期内容吧），假设今天的“每日密钥”是BKG，发报员想出来的指标组是ATX，那么发报员发报时，需要先把密码机的转轮分别转到B、K、G的位置，然后在键盘上连续输入“ATXATX”，得到一串密文，我们假设是“GYKPWR”。在“GYKPWR”这6个字母中，如果我们知道德军运用指标组的规则（3个字母重复两次），那么我们很容易看出：第1个字母G和第4个字母P所对应的明文都是A，第2个字母Y和第5个字母W所对应的明文都是T，第3个字母K和第6个字母R所对应的明文都是X。

既然如此，为什么同一个明文字母，在不同的位置上会得到不同的密文呢？这是个很基础的问题，我想你可以秒答——因为Enigma每输入一个字母，转轮就会步进一格呀！没错，但这里的关键信息是，每次发报的时候，转轮的初始位置都是固定的，也就是今天的“每日密钥”BKG，而且转轮的步进方式是固定的，这意味着什么呢？假如发报员一天发了100封电报，那么每封电报的开头都需要先加上指标组，每封电报的指标组可以都不—样，但用来加密这些指标组的换字表却是完全一样的！

上面这段话似乎不太容易理解？没事，我们还是看例子。假如发报员今天发了100封电报，每封电报的开头都需要加上指标组，机器转轮的初始位置都是“每日密钥”BKG。当按下指标组的第1个字母时，最右侧的转轮步进一格，也就是从G转到了H的位置；再按指标组的第2个字母，最右侧的转轮又步进一格，也就是从H转到了I的位置。以此类推，发报员输入指标组的6个字母时，所对应的最右侧转轮的位置永远是GHIJKL，别说发100封，就是发10000封电报，这个对应关系也都是完全固定的。

特征结构

不过，这个规律又意味着什么呢？小雷发现，利用这个规律，可以把相同明文字母产生的密文字母串联起来，形成一种循环序列。我们还是来举个例子，假设小雷每天能够收到很多封用Enigma加密的电文，每封电文使用的指标组都不一样，但是用来加密这些指标组的“每日密钥”却都是相同的。小雷把每封电文的前6个字母，也就是加密之后的指标组给提取出来，因为指标组是3个字母重复两次，所以小雷也把它们写成3个字母一组，比如有3封电文的前6个字母分别是这样的：

1.DMO VBN

2.VON PUY

3.PUC FMO

由于指标组里面第1/4、2/5、3/6个位置的明文字母是相同的，转轮步进的距离也是相同的，因此小雷就把这6个字母分为（1/4）（2，5）（3/6）这三个组。先看（1/4）组，电文1的（1，4）组是D和V两个字母，电文2的（1/4）组是V和P，电文3是P和F，于是我们可以把这3条电文的（1/4）组串联起来，写成DVPF。如果我有更多的电文，这个序列还可以继续写下去，直到又返回第一个字母D为止，这样就形成了一个循环序列。只要一天中的电文足够多，小雷就可以把26个字母全部凑齐，这时就可以得到一个或者多个循环序列，但每个序列的长度可以不一样，例如：

（1/4）=（DVPFKXGZYO）（EIJMUNQLHT）（BC）（RW）（A）（S）

我们发现最后有两个落单的A和S，这意味着如果第1个字母出现了A或S，那么第4个字母也一定是A或S，也就是说这个循环序列里只有一个字母。以此类推，（2/5）和（3/6）组也可以用同样的方法来操作，得到：

（2/5）=（BLFQVEOUM）（HJPSWIZRN）（AXT）（CGY）（D）（K）

（3/6）=（ABVIKTJGFCONY）（DUZREHLXWPSMO）

小雷指出，在每一组循环序列中，长度相同的序列总是成对出现，比如（1/4）组中的6个序列，长度分别为10、10、2、2、1、1，你看，果然都是成对出现的。你可能要问了，这难道是巧合吗？别忘了，小雷是个数学大牛，对于数学家来说，怎么能允许巧合这种东西呢？所有数学命题，都是需要进行证明的呀！于是小雷对他发现的这个规律进行了证明，这个证明使用了19世纪的法国数学天才埃瓦里斯特-迦罗瓦（Evariste Galois）所开创的“群论”这一数学领域中的方法。群论这个东西属于抽象代数，就算是大学里的高等数学，也只有数学、物理这种特别“硬”的专业才会学到，所以就连小雷本人在《IEEE计算史纪事》上的那篇文章中都说“证明过程太长，我就省略了”，估计写出来大部分人也看不懂——当然了，我也是看不懂的，哈哈。

小雷把上面这三组序列称为“特征结构（characteristic structure）”，由于特征结构只和每日密钥有关，很显然，在同一天里，特征结构是固定不变的。虽然我们没办法在这里解释小雷的数学证明，不过我们倒是可以简单解释一下为什么会出现这样的结构。

我们在最早介绍Enigma设计原理的时候提到过，Enigma上有一个很聪明的设计叫反射器，有了反射器，一台Enigma就可以同时完成加密和解密两种操作，也就是说，当转轮位置相同时，按下明文字母就会得到密文，而按下密文字母就会得到明文。反射器其实也是一个转轮，只不过它不会转，而且一般的转轮两面各有26个触点，而反射器只有单面26个触点，它里面实际上是把这26个触点两两连成了一对，组成了13个反射回路，因此在任何一个状态下，字母1沿着回路到达字母2，字母2也一样能沿着相反的回路回到字母1。

尽管反射器特别好用，可是小雷一看就发现，这种两两结对的设计，其中就蕴含了某种数学规律，这个数学规律用简单的话来说，就是明文字母和密文字母之间的置换是“完全互斥”的。通过这一规律，小雷就可以证明由指标组产生的特征结构，就必定是由像上面那样成对出现的循环序列组成的。

“雷氏定理”

不过话说回来，即便我知道了这个规律，我怎么用它来破译密码呢？要知道，数学的精髓就是通过一条规律推导出更多的规律，特别是像小雷这种天才数学家，一定不会放过这里面所蕴含的玄机。小雷发现，通过上面这个基本规律，可以推导出另外一条更重要的规律：

一对相互置换的字母，在某一组中一定分别位于两个同长度的不同循环序列中，且其相邻的字母（一个在右，另一个在左）也一定为相互置换的关系。

上面这句话几乎就是小雷的原话直接翻译过来的，我们就管它叫“雷氏定理”吧。说实话，这句话到底在说什么，特别是后半句到底是什么意思，我也是琢磨了半天才搞明白，还是拿个例子来解一下吧。

我们假设德军有一个发报员特别偷懒，他经常拿AAA、BBB这种重复的字母组合来做指标组——比如说他今天就用了个AAA吧。然后我们已经掌握了今天的特征结构，也就是上面那三组序列，我们可以发现，在（1/4）组中，有两个序列分别都只有1个字母，即A和S。根据雷氏定理，相互置换的字母一定位于两个同长度的不同循环序列中，那么A和S一定是相互置换的关系，换句话说，在第1/4个字母的位置上，A一定会被加密成S，反过来，S也一定会被加密成A。

既然如此，我们就可以把所有形如“S？？S？？”的指标组都给筛选出来，看看它们当中有没有谁是AAA呢？假如说我们找到了三個符合条件的指标组，分别是：①SUG SMF；②SJM SPO；③SYX SCW。好了，我们继续往下验证。

先看①号选手。假设它就是AAA，那么第2个字母就是把A加密成了U，换句话说，在第2个字母位置上，A和U应该是相互置换的关系。但是我们看（2/5）组的序列，A所在的序列长度是3，而U所在的序列长度是9，它们并不位于“同长度”的序列中，因此①号选手不可能是AAA。②号选手也栽在了相同的地方：第2个字母J所在的序列长度也是9，所以它也被毙掉了。

现在只剩③号选手。它的第2个字母Y所在的序列长度是3，通过；第3个字母X呢，因为（3/6）组只有两个长度为13的序列，只要A和X不在同一个序列就OK了，很显然，这一关也通过了。我们还发现，第2个字母Y和第5个字母C，以及第3个字母X和第6个字母W，在各自组的序列中都是相邻关系，即（2/5）组中，C在Y的右边（Y是最右边一个字母，因此它的右边就回到了最左边），（3/6）组中，W在X的右边，这也符合雷氏定理的后半句。因此，③号选手就极有可能真的是指标组AAA。

通过这种方法，小雷就可以通过猜测一些常见的指标组明文，然后根据当天的特征结构来验证和筛选出它所对应的指标组密文，这样一来就可以建立起一些明文和密文的对应关系，在密码学上这种方法被称为“已知明文攻击（known plaintext attack）”。而尤其值得赞叹的是，小雷既不需要知道每日密钥到底是什么，也不需要知道密码机的每个转轮内部的接线方式是什么，只使用数学方法就能够分析出这些信息，这真的是只有数学家才能做到的“神之一手”。

（当然，只知道这些信息还并不足以破译Enigma加密的电文，至于小雷他们到底是如何获得更多线索的，我们下期继续讲。）