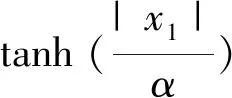基于双曲正切趋近律的永磁同步电机滑模控制

沐俊文,王仲根,聂文艳

(1.安徽理工大学电气与信息工程学院,安徽 淮南 232001；2. 淮南师范学院机械与电气工程学院，安徽 淮南 232001)

永磁同步电动机(permanent magnet synchronous motor，PMSM)具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高，以及电机的形状和尺寸可以灵活多样等显著优点。近年来，随着永磁材料性能的进步，以及永磁电机控制技术的完善，PMSM在工业领域有着广泛应用。但是，PMSM是多变量、强耦合、非线性和变参数的复杂对象，为了获得优良的控制性能，需要研究一些可靠的控制算法。目前，三相永磁交流调速矢量控制系统中的速度控制器普遍采用传统的PI调节器，其算法简单，可靠性高及参数整定方便。但是，当PMSM这一复杂系统受到外界扰动影响或电机内部参数变化时，传统的PI控制方法就不能满足控制系统的要求[1-5]。近年来，各种性能优越的算法被引入PMSM的控制系统来解决上述问题，如神经网络控制、模糊控制、滑模变结构控制等[6-9]。滑模控制因其对扰动与参数不敏感、响应速度快等优点得到广泛应用，成为研究热点[10]。文献[11]将滑模变结构控制引入PMSM直接转矩控制中来解决传统PMSM直接转矩控制中的电流磁链和转矩脉动大的问题；文献[12]提出一种新型变指数趋近律滑模变结构控制策略来解决PMSM传统直接转矩控制中磁链转矩脉动大等问题；文献[13]将神经网络和滑模控制结合，提出了一种基于神经网络的PMSM自适应滑模控制方案，来减弱“抖振”现象，但是上述传统的基于指数趋近律的PMSM滑模控制因其系统抖振大，参数整定复杂，需要研究更加简单稳定的控制算法[14]。

为提高PMSM滑模控制的性能，本文提出一种基于双曲正切趋近律的滑模控制方案，该控制方案在指数趋近律的基础上，引入双曲正切函数来提高PMSM滑模控制系统的性能，减小了系统因突加负载而引起的转矩、转速变化，抑制了系统稳定运行时的转速脉动。

1 双曲正切趋近律

趋近律的设计可以保证系统从任意初始状态趋向切换面，直到到达切换面这一运动过程的品质，因此趋近律的设计必须尽量缩短趋近运动的时间，保证系统的稳定。本文提出一种双曲正切趋近律，其表达式为

(1)

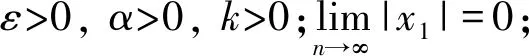
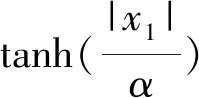
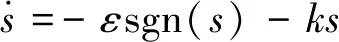
(2)

这是一个指数趋近律，可知指数项-ks能保证当s较大时，系统状态能以较大的速度趋近于滑动模态，而与ε无关。

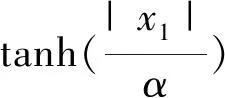
通过上述分析可知，本文设计的双曲正切趋近律，保留了指数趋近律快速趋近的特点，同时因为引入了双曲正切函数消除了系统抖振，设计简单。

2 滑模速度控制器的设计

为便于设计滑模速度控制器以验证新型趋近律的实际效果，本文以表贴式PMSM电机为控制对象，其定子电感满足Ld=Lq=Ls，首先建立d-q坐标系下的数学模型[15-16]

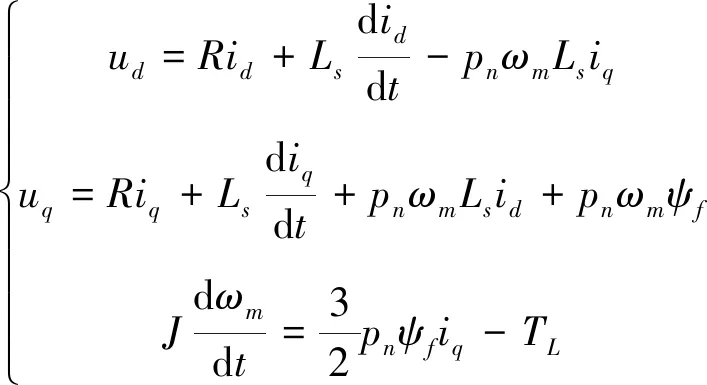
(3)

式中：ud、uq分别是定子电压的d-q轴分量；id、iq分别是定子电流的d-q轴分量；Ls为定子电感；R为定子电阻；ψf为永磁体磁链；ωm为电机的机械角速度；pn为极对数；；TL为负载转矩；J为转动惯量。为了使表贴式PMSM获得较好的控制效果，将采用令id=0的转子磁场定向控制方法，此时式(3)则可变为如下的数学模型

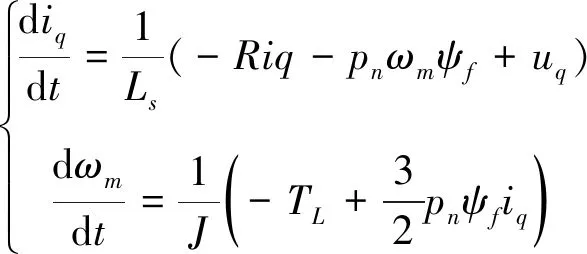
(4)

定义PMSM系统的状态变量为

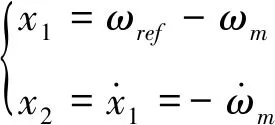
(5)

式中：ωref为电机的参考转速，ωm为电机实际转速。根据式(4)、(5)可知

(6)

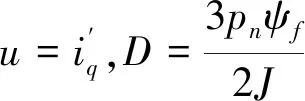
(7)

定义滑模面函数为s=cx1+x2(c>0)，并求导，可得

(8)

这里采用本文设计的双曲正切趋近律方法来设计控制器，可得控制器的表达式为

(9)

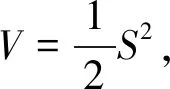
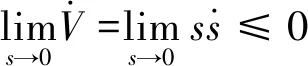
(10)

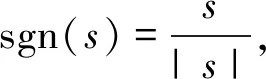
(11)

3 仿真验证

根据上述控制器的设计，建立三相PMSM矢量控制系统仿真模型如图1所示。其中，仿真中所用电机的参数设置如表1所示。仿真条件设置为：Udc=311V，PWM开关频率设置为fpwm=10kHz，采样周期设置为Ts=10μs，采用变步长ode23tb(ode23tb是TR-BDF2的一种实现，TR-BDF2是具有两个阶段的隐式龙格-库塔公式)算法，相对误差设置为0.0001，仿真时间设置为0.4s，参考转速Nref=1000r/min，初始时刻负载转矩TL=0N·m，在t=0.2s时负载转矩TL=10N·m， 基于双曲正切函数的滑模控制器参数设置为c=60，α=1，k=300，ε=20， 限幅为-30～30A， 相同条件下， 采用指数趋近律设计控制器仿真运行，指数趋近律滑模控制器(sliding mode control， SMC)参数设置为c=60，q=300，ε=200，限幅为-30～30A，仿真结果如图2所示。

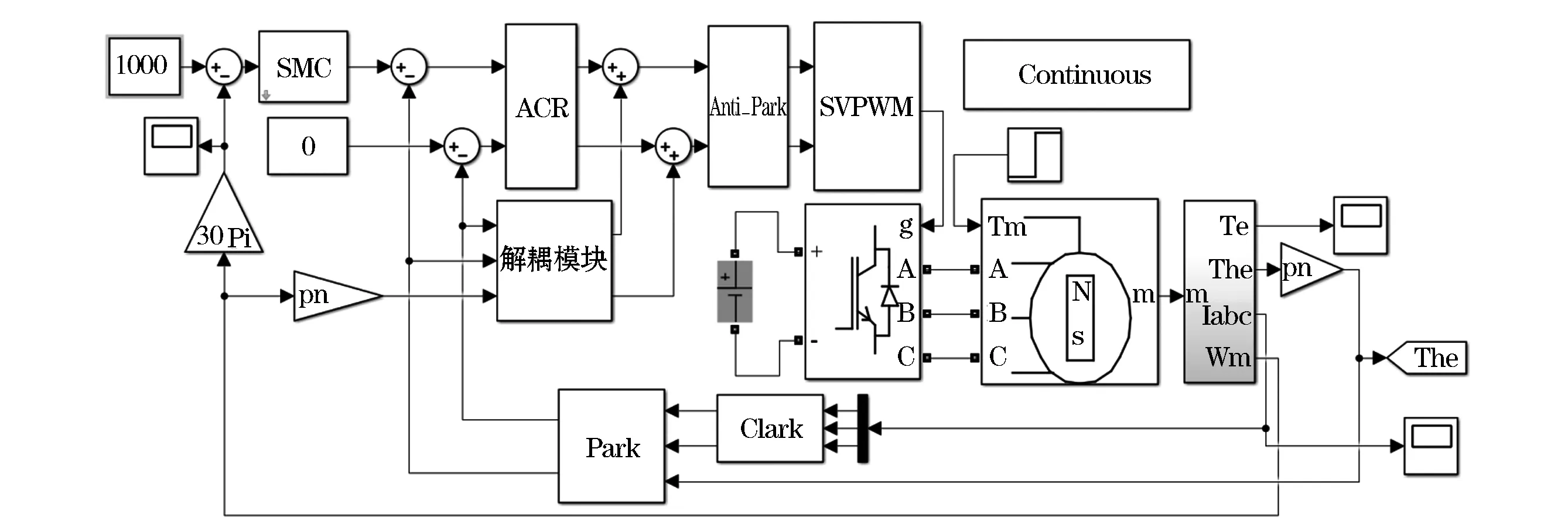
图1 三相PMSM矢量控制系统仿真模型

参数数值 极对数pn4 定子电感Ls/mH8.5 定子电阻R/Ω2.875 磁链ψf/Wb0.175 转动惯量J/(kg·m2)0.003 阻尼系数B/(N·m·s)0.008

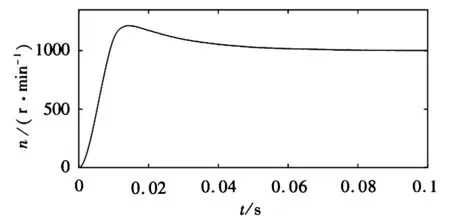
(a) 双曲正切SMC控制下的起动响应

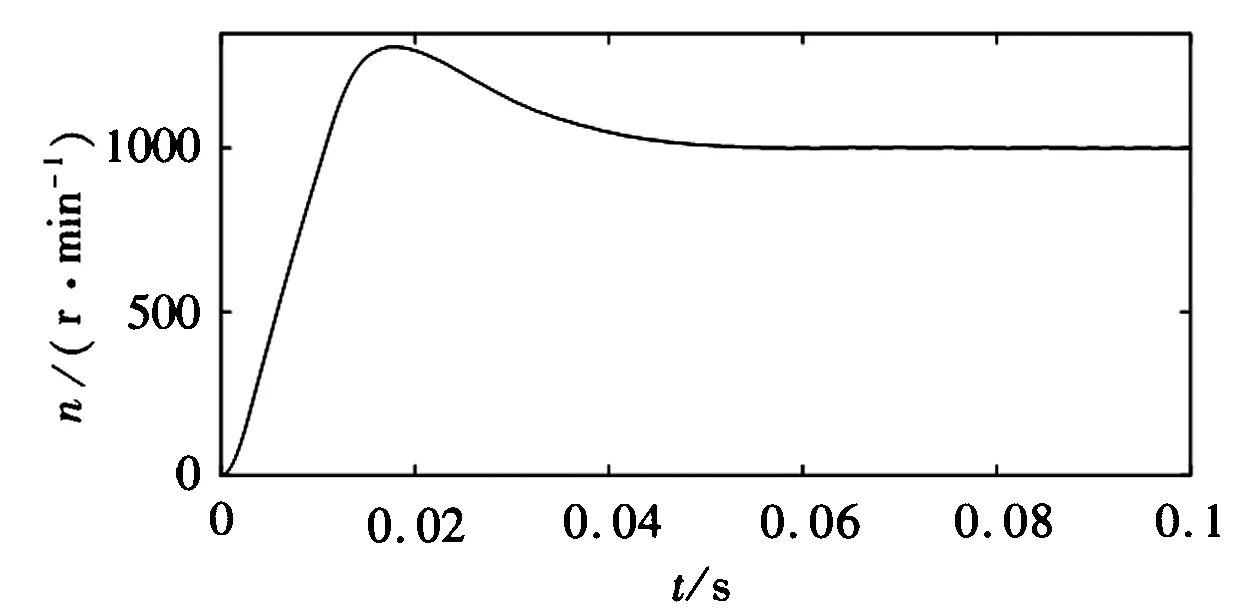
(b) 指数SMC控制下的起动响应

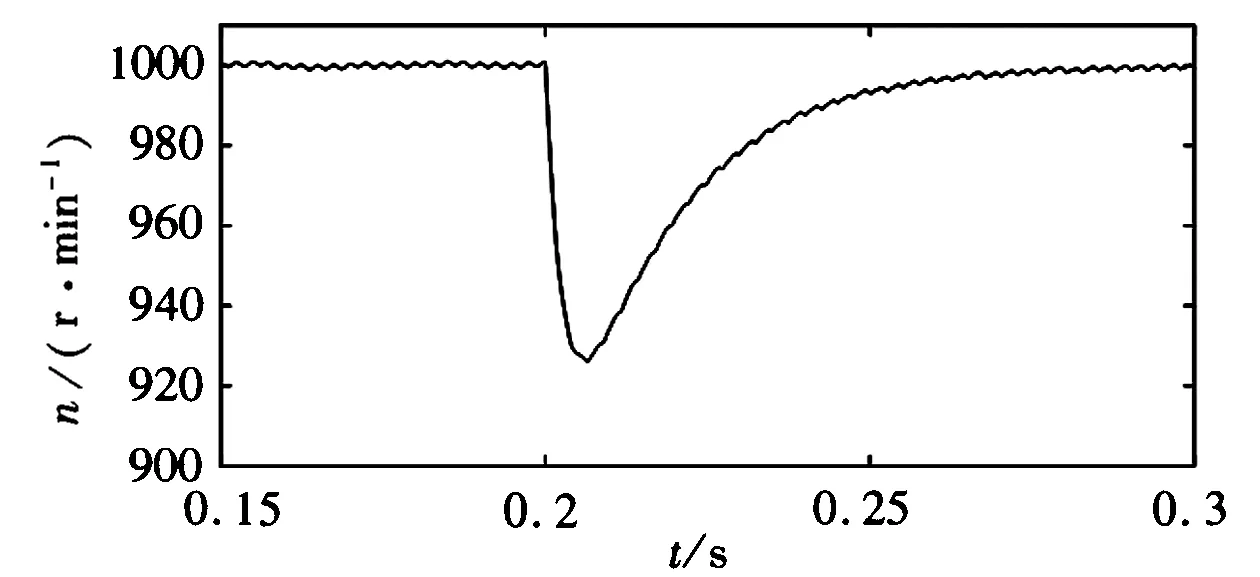
(c) 双曲正切SMC控制下的突加负载转速响应

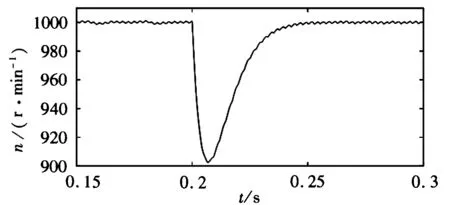
(d) 指数SMC控制下的突加负载转速响应

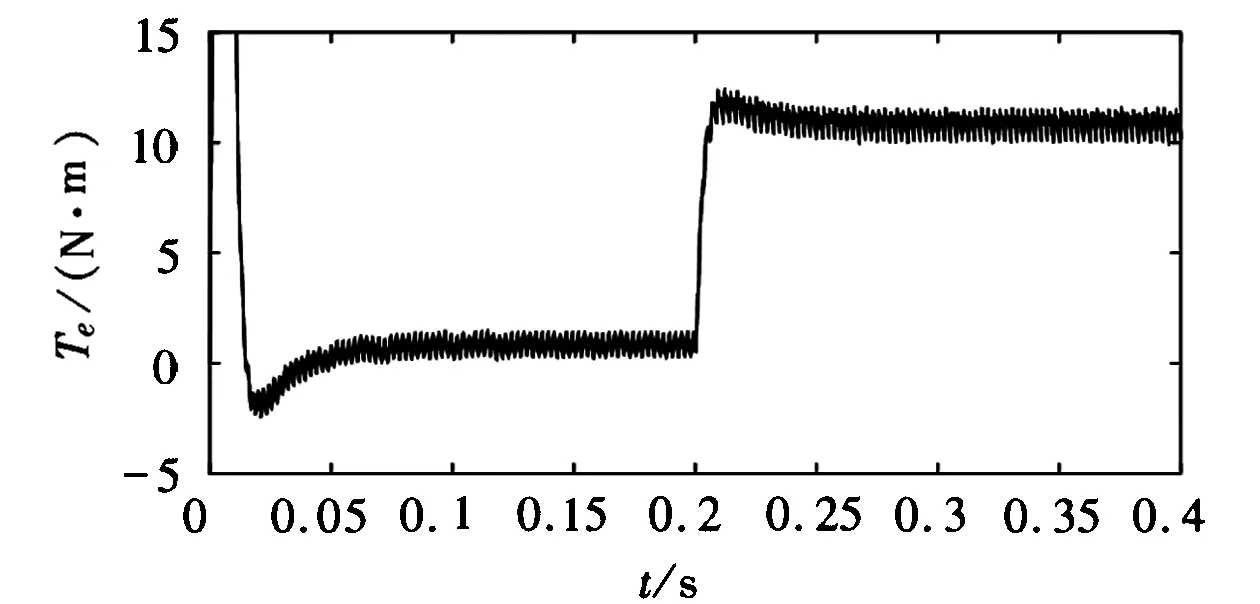
(e) 双曲正切SMC控制下突加负载转矩响应

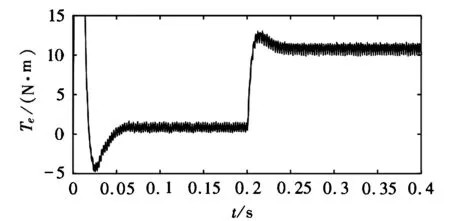
(f) 指数SMC控制下突加负载转矩响应图2 永磁同步电机启动与突加负载动态响应仿真结果

从图2(a)，图2(b)两图的比较可以看出，永磁同步电机滑模速度控制器在指数趋近律基础上引入了双曲正切函数后，在双曲正切SMC控制下，电机起动峰值时间减少了0.004s，超调量由30.9%下降到21.4%，即起动响应更快，超调更小；从图2(c)，图2(d)两图的比较可以看出，基于新型趋近律的滑模控制系统突加负载后，电机转速由902r/min变为926r/min，即转速变化小，能快速恢复到给定转速；从图2(e)，图2(f)两图比较可以看出，新型滑模控制系统在起动时，转矩下降减少50%，稳定后转矩脉动减少0.2N·m，突加负载时，转矩上升减少1N·m，可见电机转矩波动更小，系统鲁棒性更好。

4 结论