松弛模系矩阵分裂迭代法求解一类非线性互补问题
王 艳, 殷俊锋, 李 蕊,2
(1. 同济大学 数学科学学院, 上海 200092; 2. 嘉兴学院 数理与信息工程学院, 浙江 嘉兴 314001)
给定大型稀疏矩阵M∈Rn×n和n维向量q∈Rn,考虑如下一类非线性互补问题:求向量z,w∈Rn满足
z≥0,w∶=Mz+q+f(z)≥0,zTw=0
(1)
这里,f:Rn→Rn为给定的n元函数且满足对角可微[1-2],即fi,f的第i个分量仅仅是zi的可微函数. 其中不等号是分量意义下的不等号,zT表示向量z的转置,特别地,当函数f为线性函数时,问题(1)化为线性互补问题.
互补问题在科学与工程等领域有着广泛的应用[3-4], 如变分不等式、弹性接触问题、期权定价等自由边界问题均可化为互补问题. 由于互补问题的重要性,引起了数学工作者的广泛关注和高度重视. 近几十年来, 其数值解的研究发展迅速,取得了丰硕的成果. Bai[5]提出了求解线性互补问题的模系矩阵分裂迭代法,并且为模系矩阵分裂迭代方法提供了一个基本框架. 由于其迭代格式简单,在文献[5]的基础上,模系矩阵分裂迭代法得到了进一步研究,比如,两步模系矩阵分裂迭代法[6]、加速的模系矩阵分裂迭代法[7]和松弛模系矩阵分裂迭代方法[8]等. 随着高性能并行计算机系统的快速发展,Bai等[9]利用并行计算的思想, 提出了模系同步多分裂迭代法、模系同步二级多分裂迭代方法[10]和两步模系同步多分裂迭代方法[11].
针对非线性互补问题(1), 当函数f对角可微时, Xia等在文献[12]中首次将求解线性互补问题的模系矩阵分裂迭代法推广至该非线性互补问题, 构造了相应的模系矩阵分裂迭代法, 并给出了系数矩阵为正定或H+-矩阵时的收敛理论. 随后, Li等[13]采用加速模系矩阵分裂迭代法对该非线性互补问题进行求解, 并且给出了矩阵M为H+-矩阵时的收敛性分析. 本文提出用松弛模系矩阵分裂迭代法求解该非线性互补问题, 讨论该迭代法在系数矩阵M为H+-矩阵时的收敛条件, 并且给出了最优参数的选取. 数值实验表明, 对于大型稀疏非线性互补问题, 松弛模系矩阵分裂迭代法不仅是有效的, 而且收敛效果优于模系矩阵分裂迭代法.
1 松弛模系矩阵分裂迭代法
算法1[12]令M=F-G为矩阵M的一个分裂,给定初始向量x(0)∈Rn, 对于k=1,2,…, 从下列方程组中解出x(k):

为了提高计算效率,下面给出松弛模系矩阵分裂迭代方法.
对于任意给定的正对角矩阵Ω和Γ,令z=Ω(|x|+x),w=Γ(|x|-x),MΩ=FΩ-GΩ为MΩ的一个分裂,x满足如下不动点方程
(Γ+FΩ)x=GΩx+(Γ-MΩ)|x|-(q+f(z))
(2)
在不动点格式(2)对应的迭代格式中,考虑对原向量和更新的向量做一个加权,通过引入一个非奇异的参数矩阵P∈Rn×n,建立如下松弛模系矩阵分裂迭代方法.
算法2 对于任意给定的正对角矩阵Ω和Γ,令MΩ=FΩ-GΩ为矩阵MΩ∈Rn×n的一个分裂. 给定初始向量x(0)∈Rn,对于k=1,2,…,通过求解如下系统:
(3)
得到x(k),令z(k)=Ω(|x(k)|+x(k)).
系统 (3) 等价于

(Γ-MΩ)|x(k-1)|-q-f(Ω(|x(k-1)|+x(k-1)))]
(4)
算法2提供了松弛模系矩阵分裂迭代方法的一个基本框架. 特别地,取
当α,β分别取α=β,α=β=1和α=1,β=0时,称为松弛模系逐步超松弛迭代格式(RMSOR)、 松弛模系高斯-赛德尔迭代格式(RMGS)和松弛模系雅克比迭代格式(RMJ).

特别地,令P=εI, 系统 (3) 等价为如下形式:
(5)
这里,ε∈R{0}, 并且ε随着k的变化而变化.
2 收敛性分析
H+-矩阵在数学物理问题、控制论、电力系统理论、经济数学以及弹性力学等众多领域中都有广泛应用,例如经济价值模型、 反网络分析模型、经济学中的投入产出增长模型和概率统计中的Markov链等问题.
给定两个实矩阵M=(mij),N=(nij)∈Rm×n, 如果对任意的1≤i≤m,1≤j≤n都有mij≥nij(mij>nij), 则记M≥N(M>N). 本文用记号|M|=(|mij|)∈Rm×n表示M的绝对值.
令M∈Rn×n为一个实n×n矩阵,它的比较矩阵〈M〉=(〈m〉ij)定义为
若对任意i≠j, 有mij≤0, 则称M为Z-矩阵. 若M为非奇异的Z-矩阵且M-1≥O,O为零矩阵, 则称M为M-矩阵. 如果〈M〉为M-矩阵, 则称M为H-矩阵. 对于H-矩阵M, 有M非奇异, 且|M-1|≤〈M〉-1. 特别地, 对角元为正的H-矩阵称为H+-矩阵.
给定M∈Rn×n, 设M=F-G, 如果F非奇异, 则称M=F-G为矩阵M的一个分裂; 如果F是非奇异的M-阵并且G≥0, 则称分裂为M-分裂;当〈F〉-|G|是一个M-矩阵,则称M=F-G是一个H-分裂;如果〈M〉=〈F〉-|G|, 则称分裂为H-相容分裂.
引理1[14]如果矩阵M∈Rn×n是严格对角占优的,对于任意矩阵N∈Rn×n,

引理2[15]矩阵M是一个对角元为正的Z-阵,M是一个M-阵当且仅当存在一个正对角矩阵D, 使得MD是对角元为正的严格对角占优矩阵.
引理3[8]令M∈Rn×n是一个H+-矩阵,MΩ=FΩ-GΩ为矩阵MΩ的H-分裂.则存在一个正对角矩阵D使得(〈FΩ〉-|GΩ|)D和(Γ+〈FΩ〉)D是两个严格对角占优矩阵,且有
[(〈MΩ〉+〈FΩ〉-|GΩ|)De]i>0,i=1,2,…,n
下面,考虑算法2的收敛性. 假设对角可微函数f满足



(Γ-MΩ)|x*|-q-f(Ω(|x*|+x*))]
(6)
由于f是对角可微的,根据均值定理,有
f(z(k))-f(z*)=f(Ω(|x(k)|+x(k)))-
f(Ω(|x*|+x*))=
J(k)Ω(|x(k)|-|x*|+x(k)-x*)
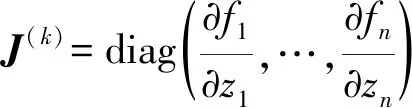
x(k)-x*=(I-P)(x(k-1)-x*)+

(Γ-MΩ)(|x(k-1)|-|x*|)-
(f(Ω(|x(k-1)|+x(k-1)))-
f(Ω(|x*|+x*)))]=
(I-P)(x(k-1)-x*)+

(Γ-MΩ)(|x(k-1)|-|x*|)-
J(k-1)Ω(|x(k-1)|-|x*|+x(k-1)-x*)]
(7)
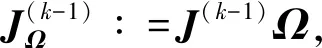
|x(k)-x*|=



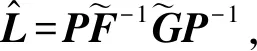
(8)
(9)
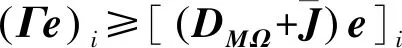
(10)
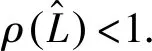

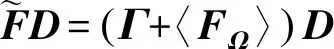

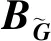
进而,有

{[Γ+〈FΩ〉-(Γ+DFΩ)|P-I|-
|BFΩ||P-I|-|BGΩ|P-|BMΩ|P]De}i.
(11)

情况1:如果(Pe)i≥1,由式(11)可得到

|BGΩ|P-|BMΩ|P]De}i≥{[Γ+〈FΩ〉-
(Γ+DFΩ)(P-I)-|DGΩ|P-(Γ-DMΩ)P-
|BFΩ|(P-I)-|BGΩ|P-|BMΩ|P]De}i=
{[2Γ+2DFΩ-(2Γ+|FΩ|+|GΩ|-
〈MΩ〉)P]De}i>0
(12)
情况2:如果0<(Pe)i<1,有

|BGΩ|P-|BMΩ|P]De}i≥{[Γ+〈FΩ〉-
(Γ+DFΩ)(I-P)-|DGΩ|P-(Γ-DMΩ)P-
|BFΩ|(I-P)-|BGΩ|P-|BMΩ|P]De}i=
{[(〈MΩ〉+|FΩ|-|GΩ|)P-
2|BFΩ|]De}i>0.
(13)
结合式(12)和式(13),得到不等式(10).证毕.
基于引理4,建立如下收敛性定理.
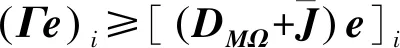
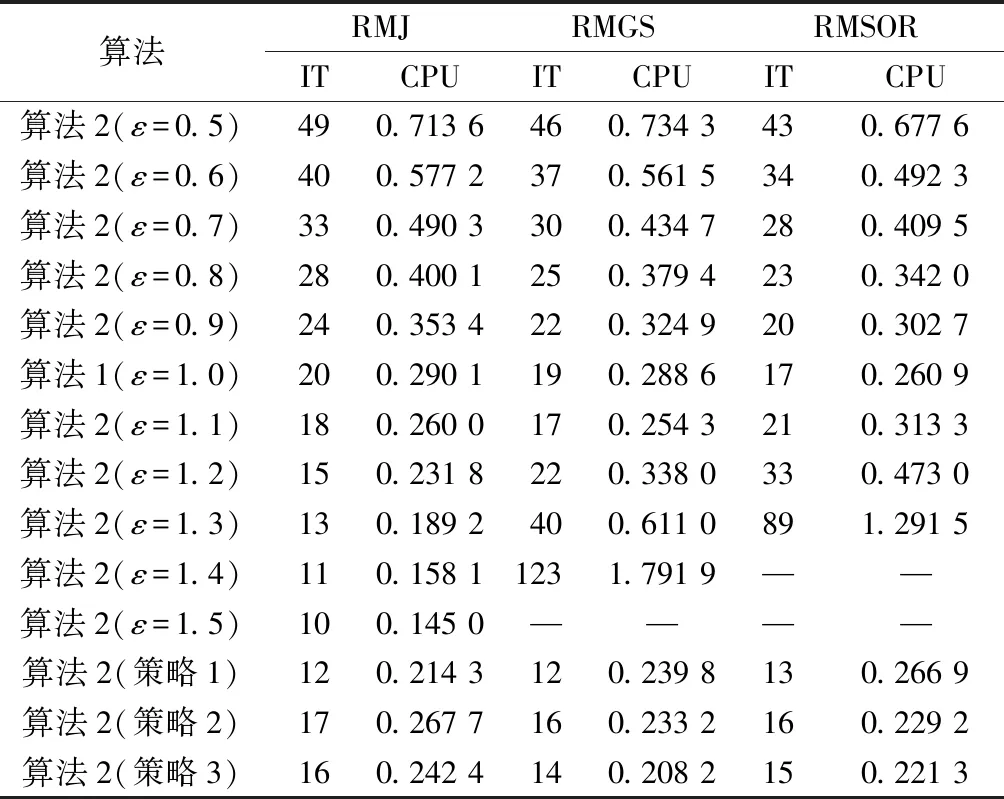
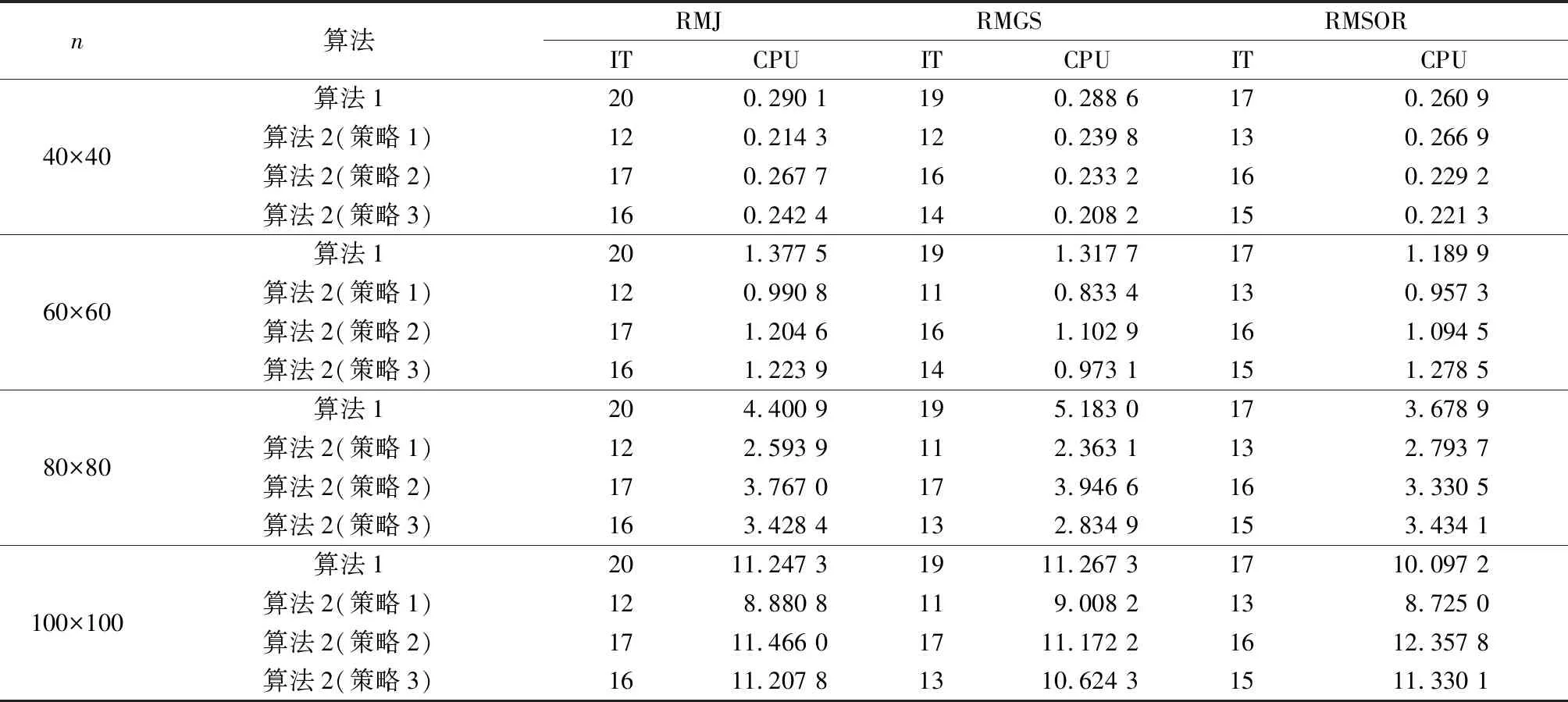
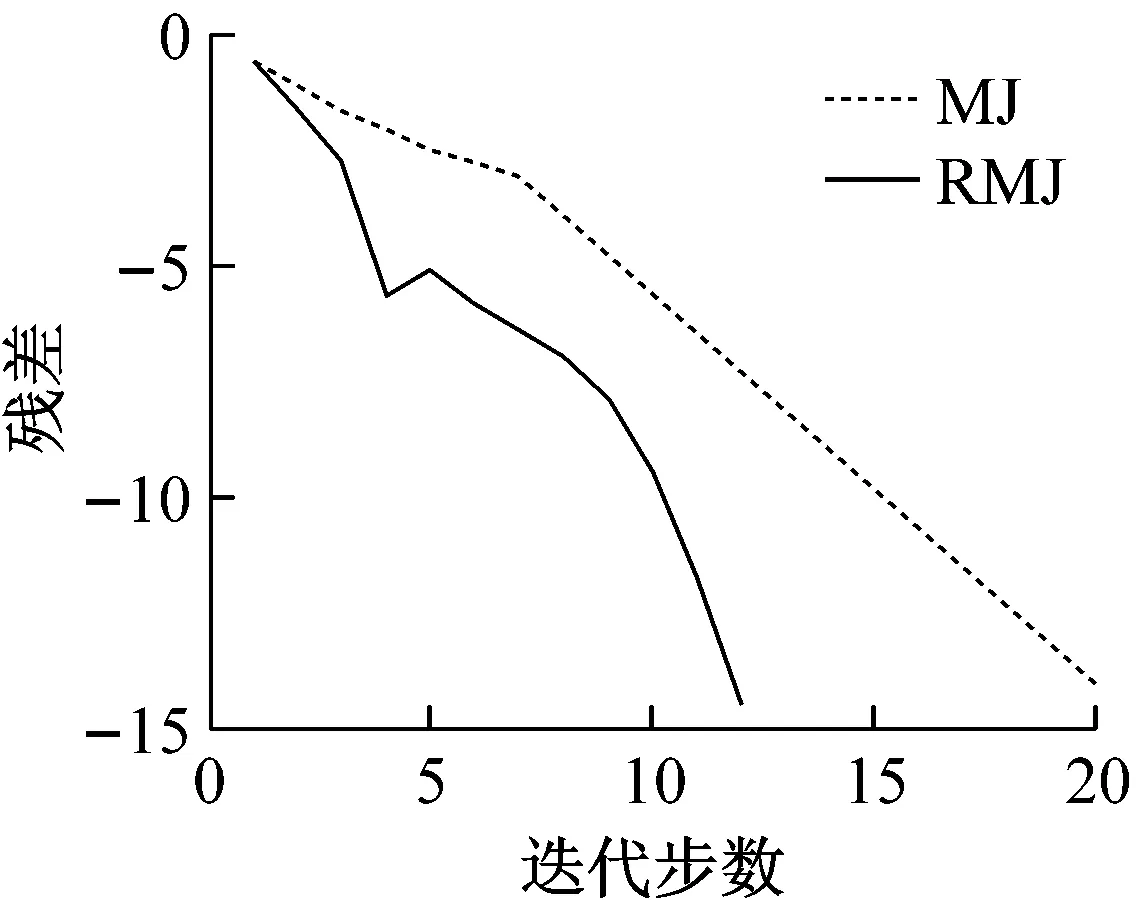
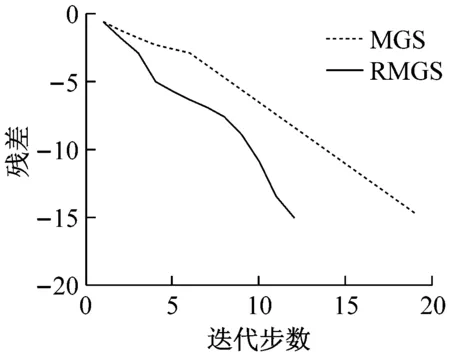
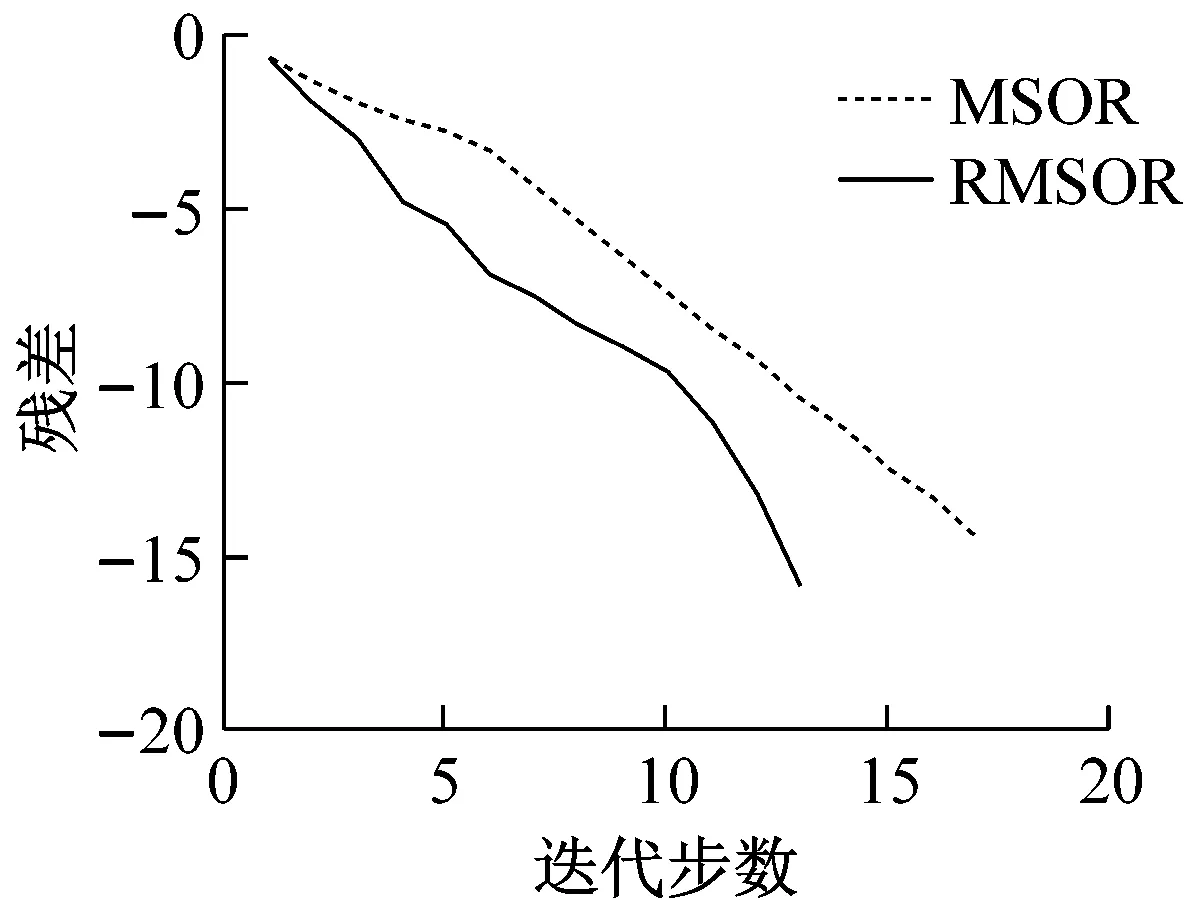
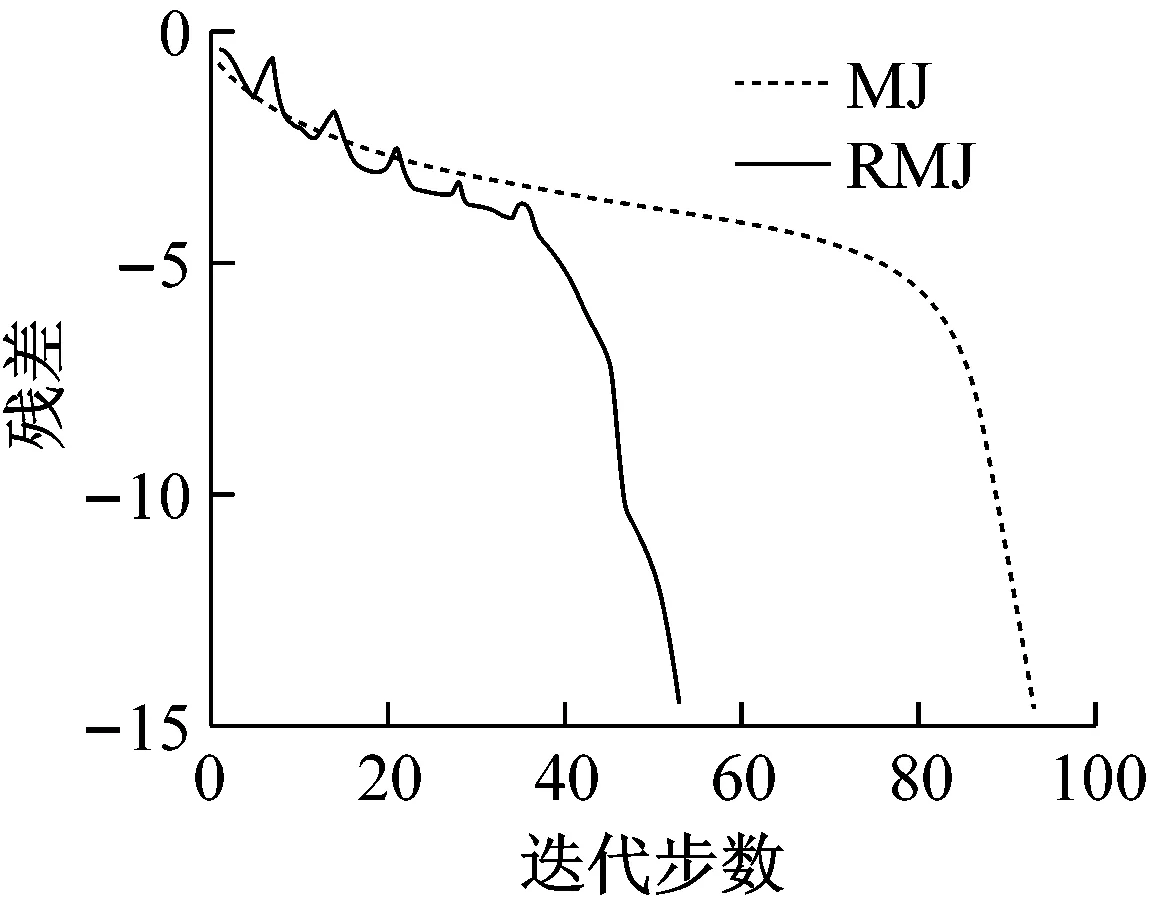
ai<ε 其中,D由引理3给出,则 i=1,2,…,n (14) 由算法2生成的迭代序列收敛到非线性互补问题(1)的解x*. [(2Γ+2DFΩ)De]i-[(2Γ+|FΩ|+|GΩ|- 〈MΩ〉)De]i=[(〈MΩ〉+〈FΩ〉- |GΩ|)De]i>0 以及 [(〈MΩ〉+|FΩ|-|GΩ|)De]i-2(|BFΩ|De)i= [(〈MΩ〉+〈FΩ〉-|GΩ|)De]i>0 然后,有0 注1 定理1给出了松弛参数ε的一个区域,可以保证算法2的收敛. 在文献[11]中,给出求解线性互补问题的理论最优参数, 由于x*未知,在具体实现时,x*用x(k-1/2)代替,并且用k-1代替k. 因此,松弛参数ε的一个合理的选择为 (15) 在第k步,松弛参数ε的选取方法如下: (16) 这里,a,b由定理1给出. 本节通过数值实验验证几种松弛模系矩阵分裂迭代法求解非线性互补问题(1)的有效性. 在数值实验中, 初始向量取为x(0)=(1,1,…,1)T∈Rn,Γ=2DM,对于MSOR方法和RMSOR方法,松弛参数取α=1.2, 停止准则设定为 所有计算均在一台CPU为2.40 GHz和内存为4.00 GB的机器上运行, 编程语言为MATLAB. 为块三对角矩阵, 其中S=tridiag(-1,4,-1)∈Rm×m为三对角矩阵, 表1给出了松弛参数ε的选取策略.对于例1,式 (14) 中取D=I. 基于定理1,通过简单地计算,对于RMJ,RMGS,RMSOR方法, 策略2中的(a,b)为 (0,1.200 0),(0.333 3,1.200 0), (0.428 6,1.133 3) (17) 策略3中(a,b)为 (0,1.333 3),(0,1.333 3),(0,1.259 3) (18) 表2分别列出当n=1 600, 松弛参数ε在0.5~1.5之间变化时几种迭代法的迭代步数(记作IT)和迭代时间(记作CPU). 从表2中可以看出,当松弛参数ε<1时,算法2需要的迭代步数和计算时间比算法1多,当ε增大时,对于RMJ方法,迭代步数和计算时间是不断下降的,而RMGS方法和RMSOR方法的迭代步数和计算时间先减少后增大. 当ε不在收敛区域时,迭代方法不收敛. 此外,ε≥1时三种方法比ε<1时收敛得快,这表明在公式 (15) 中,精确解更靠近x(k-1/2). 松弛参数的三种选取策略数值实验显示在表2的最后三行. 从表2最后三行可以看出,基于三种选取策略的算法2明显优于算法1,且策略1是最优策略. 表1 3种策略描述Tab.1 Description of three strategies 表2 例1的3种迭代法的迭代时间和迭代步数随参数ε的变化Tab.2 IT and CPU for three methods with the change of ε for Example 1 当矩阵维数不断增大时,数值实验结果显示在表3中. 从表3中可以得出,无论是计算时间还是迭代步数,基于2种策略的算法2明显优于算法1. 表3 矩阵维数变化时例1两种算法比较Tab.3 Comparison of two algorithms with the change of n for Example 1 例2 设m为给定的正整数,n=m2. 在式(1)中取 表4 例2的三种迭代法的迭代时间和迭代步数随参数ε的变化Tab.4 IT and CPU for three methods with the change of ε for Example 2 为块三对角矩阵,S=tridiag(-1,4,-1)∈Rm×m为三对角矩阵, 对于例2,式(14)中取D=diag[(〈FΩ〉-|GΩ|)-1e]. 基于定理1,通过简单的计算,对于RMJ,RMGS,RMSOR方法, 策略2的中(a,b)为 (0,1.006 2),(0.930 8,1.006 2) (18) (0.748 9,1.062 5) (19) 策略3中的(a,b)为 (0,1.294 8),(0,1.294 8),(0,1.199 1) (20) 表4分别列出当n=1 600, 松弛参数ε在0.5~1.5之间变化时几种迭代法的迭代步数和迭代时间.从表4中可以看出,当松弛参数ε<1时,算法2需要的迭代步数和计算时间比算法1多,当ε增大时,对于RMJ方法,迭代步数和计算时间是不断下降的,而RMGS方法和RMSOR方法的迭代步数和计算时间先减少后增大. 算法2的实际收敛区域比式(18)、式(19)要大,因此,收敛区域还可以进行改进. 松弛参数的三种选取策略数值实验显示在表4的最后三行. 从表4最后三行可以看出,基于三种选取策略的算法2明显优于算法1,且策略1是最优策略. 当矩阵维数不断增大时,数值实验结果显示在表5中. 从表5可以得出,无论是计算时间还是迭代步数,基于三种策略的算法2明显优于算法1. 根据实验结果,得出策略1是最优策略,在图1和图2中,分别画出基于策略1的算法2和算法1随着迭代步数变化的残差下降曲线. 从两张图中可以看出,算法2收敛速度明显快于算法1,表明提出的新方法是有效的且明显优于模系矩阵分裂迭代方法. 表5 矩阵维数变化时例2两种算法比较Tab.5 Comparison of two algorithms with the change of n for Example 2 图1 例1两种算法的残差比较 Fig.1 Residual comparison of two algorithms for Example 1 图2 例2两种算法的残差比较 Fig.2 Residual comparison of two algorithms for Example 2 本文构造了求解一类非线性互补问题的松弛模系矩阵分裂迭代法,理论上分析了当矩阵M为H+-矩阵时的收敛性,并且给出了最优参数的选取方法. 数值实验进一步验证了松弛模系矩阵分裂迭代法的有效性. 数值结果表明,松弛模系矩阵分裂迭代法无论在迭代步数还是迭代时间上均优于模系矩阵分裂迭代法.
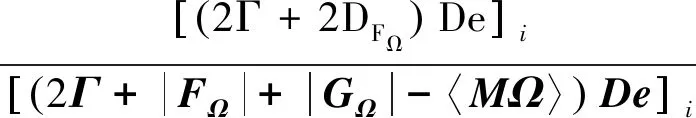

3 数值实验






4 结论

