单向阀阀芯的振动可靠性分析

王海芳,任 明,王晨炜,褚天争,李 亮

(东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004)

单向阀在液压系统中应用广泛,其结构常为锥阀形式.由于系统内油液空穴、泵的压力脉动、阀的自激振动等原因,单向阀常会产生振颤现象,进而导致管压力波动;同时,因阀芯不断与阀座撞击[1-3],导致阀座和阀芯出现凹痕,易出现渗漏,进而导致锥阀失去密封性,使液压油可以双向流动,从而导致整个液压系统功能的丧失.目前,对单向阀阀芯的分析主要集中于两方面的内容:一方面是对单向阀进行振动分析[4-5],即建立阀的振动模型,然后基于实验结果分析单向阀产生振动的原因,最后分析各因素对锥阀振动特性的影响;另一方面是对阀进行结构可靠性分析[6-7],利用可靠性理论对阀的结构进行仿真分析,最终得到结构的失效概率,有利于阀结构的优化设计.

本文以先导溢流阀的单向锥阀为例,将振动分析与可靠性的基本理论相结合,建立了表示锥阀阀芯的两种工作状态的振动可靠性功能函数;应用振动理论建立了锥阀的振动模型,选用可靠性理论中的蒙特卡洛法进行了仿真分析;应用Matlab仿真,得到了锥阀的可靠性曲线以及变异系数曲线.

1 可靠性基本理论及方法

1.1 基本原理

机械可靠性分析和设计的主要目标是求解研究对象的可靠度,设可靠度为

(1)

式中:fX(x)为研究对象包含的基本随机参数向量X=(x1,x2,…,xn)T的联合概率密度函数,状态函数Z=g(x)用以表示研究对象的两种状态,即

(2)

式中:状态函数方程g(x)=0是一个n维极限状态曲面.

1.2 振动的可靠性功能函数的建立

机械的振动设计准则包括:最大振动响应不超过许用响应;避开(或落入)共振;避开流体诱发的振动[8].而在研究锥阀的振动时,结构的1阶固有频率ωn与激励频率ω相等时,结构发生共振.根据可靠性的基本理论,离散结构失效分析的状态函数可定义为

(3)

式中:ωj为外载荷的第j个激振频率;ωni为第i个固有频率.

对于锥阀而言,常把ωni=(0.9～1.1)ωj作为共振区,这就是共振准则[9].结合式(3),可以确定离散结构的锥阀阀芯发生共振失效分析的状态函数为

(4)

而对于锥阀可靠性分析而言,为了工程计算方便,将阀视为整体,则式(4)可改写为

(5)

2 锥阀振动模型的建立

选取先导溢流阀的先导锥阀进行振动模型建立,虽然影响先导锥阀的振动与噪声的因素很多,如油液振动、空穴和液压冲击、阀的撞击和磨擦等[10-11],但在简化的振动模型中,主要考虑锥阀质量、弹簧元件的存在与油液的阻尼因素,以及外加液压振动冲击等的激励作用,构成简化的质量-阻尼-弹簧振动模型,如图1所示.

图1 先导锥阀振动模型示意图Fig.1 The schematic diagram of the vibration model ofpilot operated poppet valve

单向阀中的阀芯有一定的质量,它与弹簧一起组成了一个“质量-弹簧”振动系统,引起这个振动系统发生振动的原因无非两种情况:① 外部因素引起,即共振;② 由于自身特性引起,即自振.而本文主要研究的是共振.

当外加在振动系统上的能量源的频率与该系统的固有频率成整数倍关系时,即会发生共振.锥阀式单向阀的固有频率可按如下推导.如图1所示,其开口截面积可近似表示为

(6)

式中:S为开口截面积;d′为开口中径,d′=(d1+d)/2,d1为阀芯顶端直径,d为阀座直径;x为阀口开度;α为锥阀角度.

根据薄壁小孔节流原理[12]得

(7)

式中:Q为通过开口的流量;c为流量系数;ρ为液体密度;Δp为阀芯前后压差.

由式(7)得

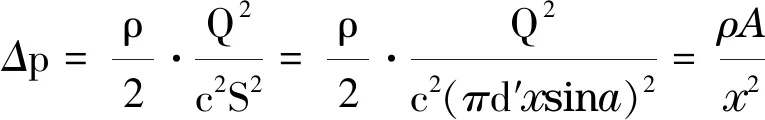
(8)

(9)

式中:A=Q2/2(cπd′sina)2(当Q一定时A为常数);x为阀口的开度.

在忽略液动力和摩擦力情况下,在开度为x0的工作点上,考虑弹簧在液压系统中的影响后,根据位移激振的强迫振动理论,运用动静法原理[13-15],得出阀芯振动微分方程为

(10)

式中:m为阀芯质量与1/3弹簧质量之和;B为阀芯承受压力差的有效面积;k为弹簧刚度.

式(10)左边第1项为惯性力,第2项为液压力,第3项为弹簧力.将式(9)代入式(10)得到

(11)

式(11)为“质量-弹簧”振动系统的无阻尼振荡的运动微分方程,其固有频率ωn表示为

(12)

将式(8)代入式(12)得

(13)

有阻尼振荡频率为

(14)

式中:ζ为阻尼比.

将式(13)代入式(14)中得

(15)

3 蒙特卡洛法仿真

3.1 蒙特卡洛法

蒙特卡洛法(Monte Carlo)是一种用数值模拟求解与随机变量有关的实际工程问题的方法,对随机变量的数值模拟相当于一种“实验”,所以蒙特卡洛法又称为统计实验法[16-17].运用蒙特卡洛法进行仿真分析有着十分重大的意义,它可以替代现实中的实验,得到与实验后基本相同的结果,从而省去大量时间、人力、财力,十分快捷有效.

由式(1)显示的可靠度是基本随机变量的联合概率密度函数fX(x)在可靠域g(x)>0中的多重积分.失效概率Pf可以表示为失效域F的指示函数IF(x)的数学期望形式,即

(16)

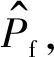
(17)

式中:RMC为蒙特卡洛法数值模拟所获得的可靠度[18-19].蒙特卡洛法数值模拟法进行结构系统可靠度分析的过程如图2所示.

图2 蒙特卡洛法可靠性分析的流程图Fig.2 The flow chart of using Monte Carlomethod to analyse reliability

3.2 估计失效概率与变异系数

(18)

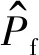
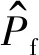
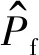
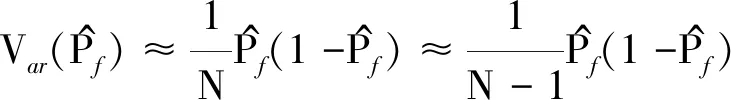
(22)

(23)

对于很小的Pf,式(21)的变异系数可写为

(24)

则所需要样本量N可以表达为给定变异系数的函数,即

(25)

若失效概率在10-k(k为整数)数量级上,且变异系数ζN=0.1,则需要N=10k+2个随机样本.若放松精度要求至ζN=0.3(中等精度),则大致需要N=10k+1样本.为了使蒙特卡洛方法估计结果具有一定精度,根据经验,一般推荐随机样本量满足

(26)

式(26)表明,至少得到10～100失效域的失效样本,才能使失效概率估计值具有较好的“平均效果”及较小的变异系数.

3.3 Matlab仿真

利用Matlab软件,通过蒙特卡洛法对液压阀阀芯的振动可靠性进行仿真[21-23],从而得到锥阀的可靠度、变异系数与样本量的关系.具体的参数如表1所示,表中m,k,d,x,ζ均服从正态分布.

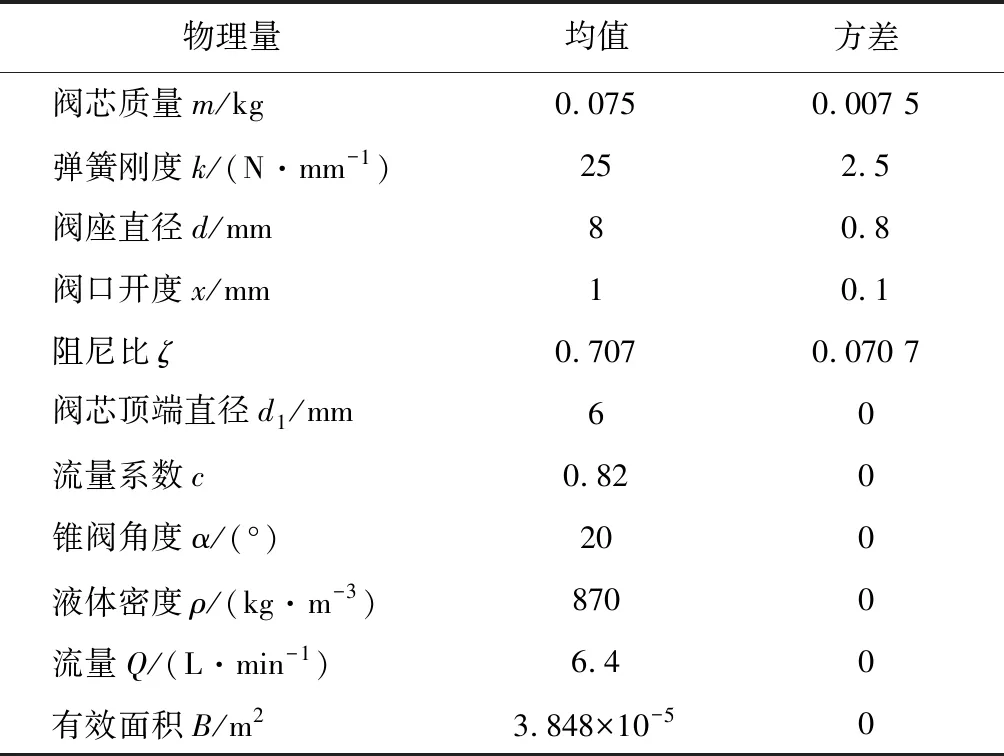
表1 液压锥阀的主要参数设置Tab.1 The main parameters of hydraulic poppet valve

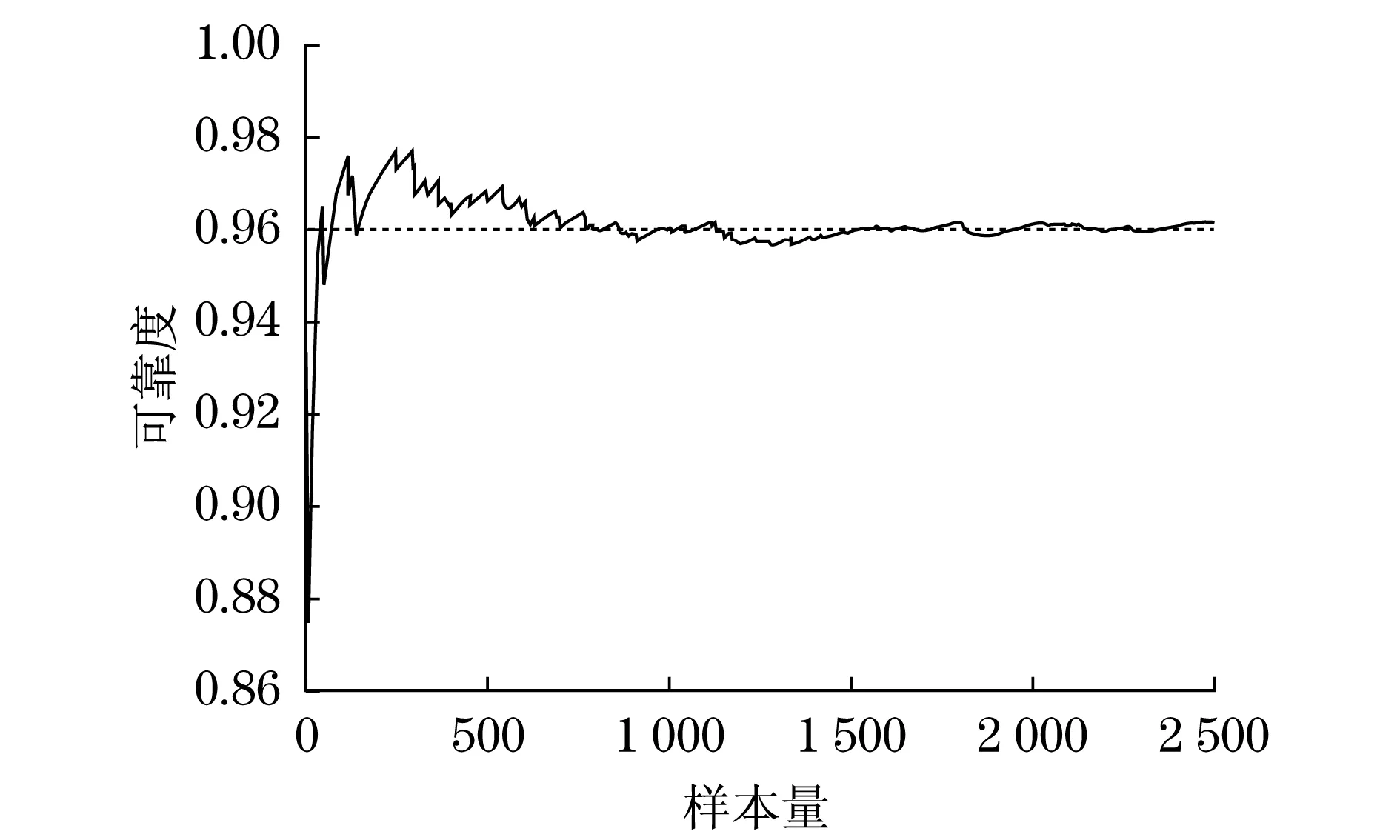
图3 N=2 500时的可靠度曲线Fig.3 Curve of reliability when N=2 500

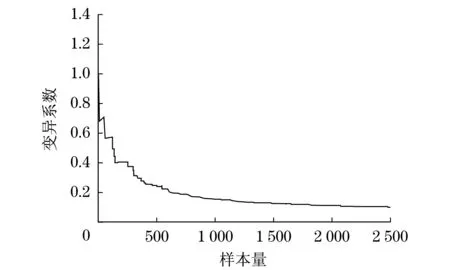
图4 N=2 500时的变异系数曲线Fig.4 Curve of variation coefficient when N=2 500

由上述数值曲线可知:当样本量N数值比较小时,可靠度的振荡幅度较大,变异系数的数值也较大;而N值越大时,可靠度以及变异系数达到平缓,当N=2 500时,根据式(24)计算可得变异系数ζN=0.1,符合图4在N=2 500时的变异系数值.因此,当样本量越大时,可靠度的估计值更接近于目标值.

4 结论

(1) 以典型液压元件锥阀为例,应用可靠性理论进行锥阀阀芯的振动可靠性分析.将机械的振动设计准则与可靠性基本理论相结合,根据位移激振的强迫振动理论,运用动静法原理,得出阀芯振动微分方程.将锥阀简化为质量-阻尼-弹簧系统的振动模型,进而求解出其无阻尼和有阻尼固有频率.结合共振准则,建立了表示锥阀阀芯的两种工作状态的振动可靠性功能函数.

(2) 基于建立的振动可靠性功能函数,应用蒙特卡洛法和Matlab对阀芯的振动可靠性进行仿真,得到了锥阀的可靠度曲线以及变异系数曲线.以其阀芯为例,在满足可靠条件的情况下,当样本量N数值比较小时,可靠度及其变异系数的振荡幅度较大,数据收敛性较差,随着N值增大可靠度及其变异系数逐渐达到平缓.当取样本量为2 500时,拟定阀芯目标可靠度为96%,相应的目标变异系数为0.1,从得到的仿真曲线中可以看出,得到的可靠度与变异系数均与目标值接近.这表明,样本量取值越大时阀芯的可靠度越接近目标值,所得到的可靠性结果精度也越高.