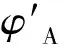220 kV MOA带电测量相间干扰的研究与分析
,
(1.国网四川省电力公司检修公司,四川 成都 610041;2.西安交通大学电气工程学院,陕西 西安 710049)
0 引 言
从20世纪80年代开始,金属氧化物避雷器(metal oxide arrester,MOA)由于具有优越的非线性特性、耐受大幅值冲击电流能力强以及运行可靠性高,在中国得到了广泛应用。MOA中的氧化锌电阻片作为重要的过电压保护元件,在长期运行中,会出现氧化锌电阻片劣化的问题,泄漏电流中的阻性电流分量不断增大,功耗变大,电阻片运行温度不断升高,发生热崩溃,发展到一定程度后将致使MOA爆炸。因此,监测持续运行电压下MOA的泄漏电流及其阻性分量,是判断MOA运行状态的重要手段。
正常情况下,避雷器的泄漏电流主要是容性电流,而阻性电流只占很小一部分。运行中,被试避雷器自身存在的相间干扰,会影响带电测量的结果,使测量结果不能真实反映避雷器的运行状况。因此,准确、有效地分析MOA的相间干扰,可以使得带电监测的结果更能反映真实情况[1-6]。
下面提出了一种“场”和“路”相结合的方法来计算MOA相间干扰,首先采用能比较精确处理多介质分布问题的有限元法来计算MOA杂散电容和相间耦合电容,再结合“路”的方法计算相间干扰电流。
1 计算原理
1.1 计算模型
220 kV电压等级的Y10W5-220/520W型MOA由2节单元组成(忽略伞群),节与节之间用金属法兰相连接,顶部有均压环罩入,底部由法兰和金属构架支撑。计算模型中各介质的相对介电常数如表1所示。

表1 各介质的相对介电常数
分别给图1(a)的1至3号导体编号为V1至V3,图1(b) 1至6号导体编号为V1到V6。

图1 有限元模型
1.2 有限元法计算耦合电容参数
电磁场理论表明电容参数与模型结构、接地体的位置有关,而与施加激励的频率、电压幅值无关,因此可在静电场条件下计算耦合电容参数。
针对模型,写出其相应的边值问题为
(1)
高压端:φ=U
(2)
低压端:φ=0
(3)
大地:φ|大地=0
(4)
无穷远:φ|r→=0
(5)
(6)
(7)
对每个单元应用数学变换,并最终整理为一个统一的矩阵方程为
[K][φ]=[V]
(8)
式中:[K]为系数矩阵;[φ]为剖分单元节点的待求电位矩阵。
求解方程得到标量电位值。对于金属氧化物避雷器,内部包括很多导体,因此,需将电容的公式推广到多导体系统。对于多导体系统,根据式(9)导体电荷、导体间电压和导体间电容的矩阵关系式可得到分布电容。
(9)
式中,Ci=Ci1+Ci2+Ci3+Ci4+Ci5+Ci6,i=1,2,3…,6。
1.3 相间干扰电流理论分析计算
求得耦合电容之后,根据基尔霍夫定律建立等效电路模型,就可以求得对应的电流值。在A相MOA底部的测量点所得到的电流iA为A相MOA总的泄漏电流,如果只考虑相邻相MOA的影响,那么它主要包括本体泄漏电流和邻相MOA通过耦合电容在A相的1、2、3号导体上作用而产生的总耦合干扰电流iBA。由于耦合干扰电流是通过电容耦合产生的,因此在相位上超前耦合电压90°,其向量关系如图2所示。

图2 仅考虑相邻耦合干扰情况下的MOA向量关系


A相和C相MOA对B相的干扰相电流IAB与ICB为幅值相同的容性电流,且关于IB的容性分量对称,所以B相MOA的持续电流容性分量减小,导致持续电流幅值减小,相位角也会有所减小。

2 仿真计算
应用电磁场有限元分析软件Maxwell 3D从“场”的角度计算出MOA的耦合电容值和杂散电容值,再运用电力系统和电子线路仿真软件EMTP的ATP程序搭建起相应的“路”模型,计算出相间干扰时的持续电流值。
2.1 有限元计算分布电容
应用电磁场有限元分析软件Maxwell 3D从“场”的角度计算出耦合电容值和杂散电容值,如表2、表3所示。

表2 独立MOA时的电容值 单位:pF
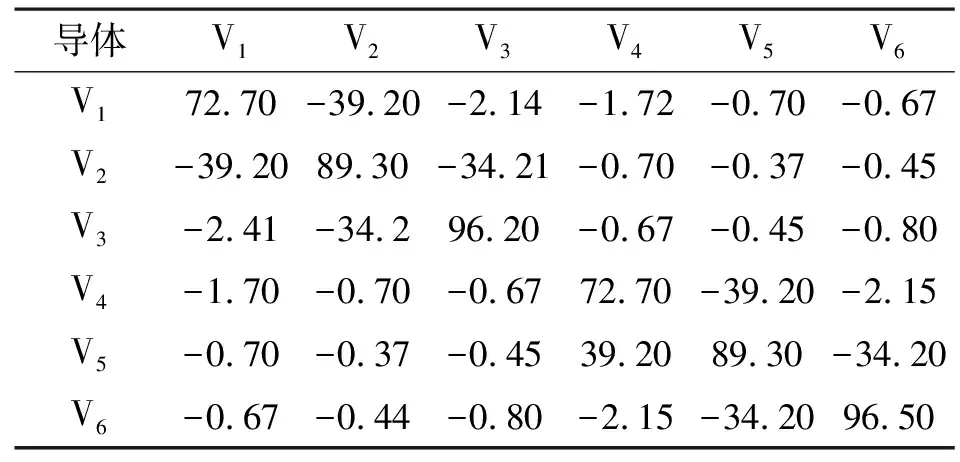
表3 干扰时的耦合电容值 单位:pF
2.2 EMTP计算持续电流
由于C相与A相的距离较远,分布电容对泄漏电流的影响程度比较微弱,故忽略不计C相与A相之间的干扰。
2.2.1 B相对A相干扰分析
220 kV的MOA每节单元有33块电阻片,在正常运行时,处于小电流区。电阻片的电阻R可以认为是固定值,其值为4400 kΩ。所以,考虑杂散电容后,Y10W5-220/520W型MOA每相的简化模型如图3所示。

图3 A相MOA考虑杂散电容的简化模型
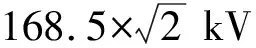

图4 未考虑相间干扰时,A相MOA的持续运行电压、电流波形
从图4可以看出,A相MOA持续运行电压峰值为238.259 kV,泄漏电流幅值为2.851 mA;泄漏电流波形超前电压波形4.57 ms,即(4.57/20)×360°=82.26°,所以泄漏电流超前电压的相位角度为:φA=82.26°。根据投影法,可以计算出阻性分量幅值为0.384 mA。
仅考虑相邻B相MOA对A相的干扰后,其电路模型如图5所示。图5中Ch1-Ch3、Cm1-Cm3、CI1-CI3分别为B相MOA的4、5、6号导体与A相MOA的1、2、3号导体间的耦合电容,计算结果如图6所示。
从图6可以看出,有B相MOA干扰后,A相MOA的持续运行电压峰值为238.259 kV,泄漏电流的峰值为2.798 mA;泄漏电流波形超前于电压波形4.454 ms,即80.01°,所以电流超前电压的相位角对比图4和图6的计算结果,可以看出,由于B相的干扰,使得A相MOA的泄漏电流从2.851 mA减小到了2.798 mA,减小了1.86%;电流超前电压的相位角从82.26°减小到了80.01°,减小了2.25°,然而电流的阻性分量幅值却从0.384 mA增加到0.485 mA,增加了26.30%。

图5 B相对A相干扰的电路模型
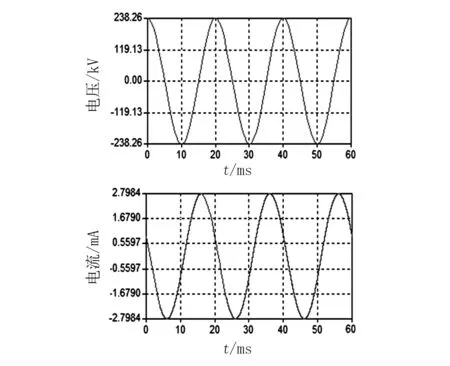
图6 B相MOA干扰时,A相的持续运行电压、电流波形
2.2.2 B相对C相干扰分析
同理,只需把上述图3和图5中的正弦电压UA换成C相持续运行电压UC就可以求出关于C的干扰情况,如图7所示。由于C相的电压和电流都滞后A相240°,所以未受干扰时C相的相位角以及泄露电流及其阻性分量都和A相的一致。
从图7可以看出,有B相MOA干扰后,C相MOA泄漏电流幅值为2.746 mA;泄漏电流波形超前电压波形4.64 ms,即83.52°。根据投影法,可计算出C相泄漏电流阻性分量幅值为0.310 mA。
对比未受干扰时的结果,可以看出,由于B相MOA的干扰,使得C相MOA的泄漏电流减小了3.683%,电流超前电压的相位角增加了1.26°,然而泄漏电流的阻性分量幅值却减小了19.27%。

图7 B相MOA干扰时,C相的持续运行电压、电流波形
2.2.3 A相和C相对B相的干扰分析
将图3中的电压相角滞后120°就可以得到B相MOA单独运行时的结果,由于B相的电流都也滞后A相120°,所以未受干扰时B相的相位角以及泄露电流及其阻性分量都和A相的一致。
考虑相邻A相和C相MOA对B相的干扰后,其电路模型如图8所示,图中CA1-CA9为A相对B相的耦合电容,CC1-CC9为C相对B相的耦合电容。仿真波形如图9所示。
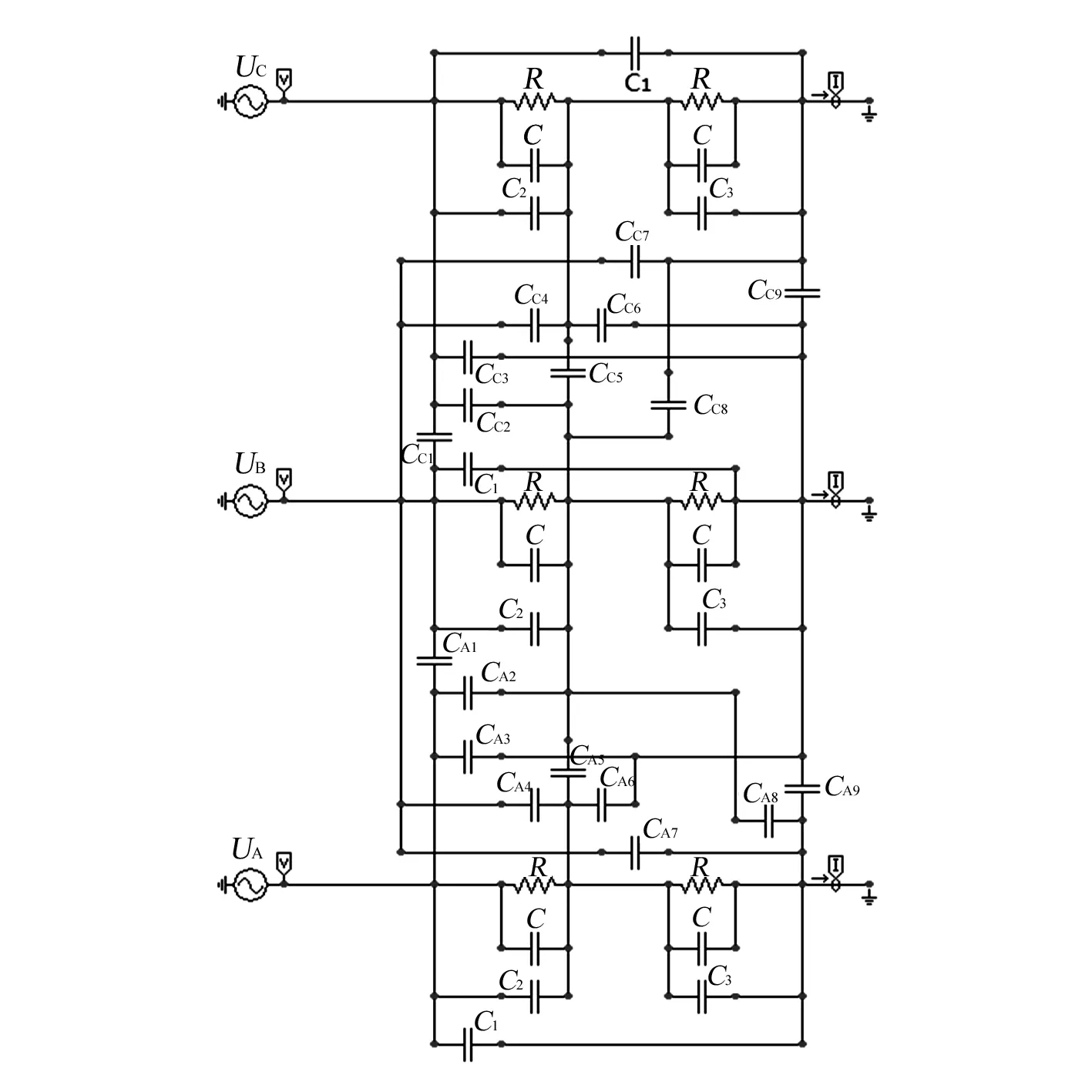
图8 A相和C相对B相干扰的电路模型
从图9可以看出,有A相和C相的干扰后,B相MOA泄漏电流峰值为2.705 mA;泄漏电流波形超前电压波形4.54 ms,即81.72°,根据投影法计算出C相泄漏电流阻性分量幅值为0.390 mA。

图9 有A相与C相MOA干扰时,B相的持续运行电压、电流波形
对比干扰前后的计算结果,可以看出:由于A相和C相的干扰,使得B相MOA的泄漏电流减小了5.12%,泄漏电流超前电压的相位角减小了0.54°,而电流的阻性分量却增加了1.56%。
3 结果分析与讨论
上节仿真结果汇总见表4,可以看出:

2)仿真数据中A、B、C三相的角度偏差分别为2.25°、0.54°、1.26°,这完全符合理论推导2°~3°的偏差范围。
3)A相和C相受B相干扰时,泄漏全电流变化幅度较小,但阻性分量变化幅度很大,分别为26.30%和19.27%;B相受A、C两相共同干扰时,全电流和阻性分量也略有变化:所以会对在线监测带来误差,尤其是阻性分量,这会影响对避雷器运行状况的正确判断。
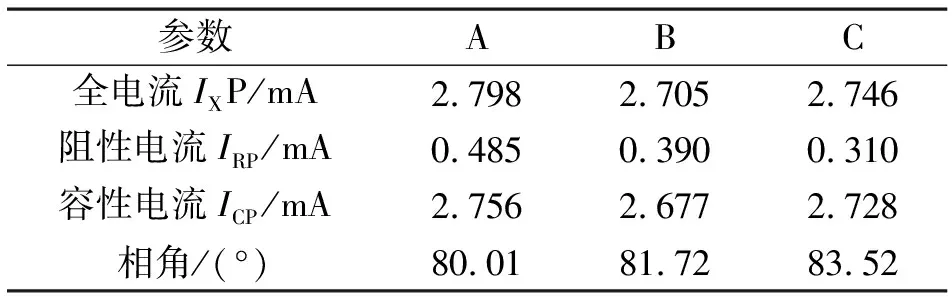
表4 Y10W5-220/520W型MOA正常运行状态下仿真数据
4 结 语