考虑分布式再生能源和储能的主动配电网可靠性评估
, ,,,
(1.国网四川省电力公司经济技术研究院,四川 成都 610041;2. 厦门大学仪器与电气系,福建 厦门 361005;3. 积成电子股份有限公司,山东 济南 250100)
0 引 言
随着电力需求的日益增长,能源危机和环境污染的不断加剧,越来越多的清洁能源被加以利用,并以分布式电源(distributed generation,DG)的形式并入电网。为了充分利用分布式清洁能源,并降低分布式能源间歇性、波动性等特点对电网的影响,主动配电网技术应运而生。
主动配电网不同于传统配电网络,除了有大电网连接以外,自身还包含了多种电源以及多个用户,增加了网络的复杂度。同时网络中还安装了主动管理设备,在多种复杂情况下可以进行不同的控制管理,更大程度发挥分布式电源的优势并尽量避免其对配电系统的干扰。因此,针对传统配电网的可靠性评估方法已经不再适用于主动配电网络[1]。近年来,国内外学者针对主动配电网的可靠性评估理论与方法展开了一系列研究。文献[2]提出的配电系统可靠性算法是基于编号法和蒙特卡洛模拟法展开的,并说明了分布式电源的接入对系统可靠性水平的提升有积极的影响。文献[3]探讨了在加入分布式电源后,配电网可靠性的研究理论和计算方法,同样说明了分布式电源并网一定程度上提高了系统的可靠性。
下面通过运用序贯蒙特卡洛模拟法,提出了一种适用于含分布式电源的主动配电网可靠性分析方法,该方法结合传统可靠性指标和针对分布式电源的可靠性指标进行研究,并解决了在评估过程中,不同系统网络类型的潮流计算与潮流平衡调整问题,总结出了完整的可靠性评估步骤。
1 可靠性评估指标
结合TOPSIS法[4]和本征向量法,综合传统可靠性指标和针对分布式电源的可靠性指标[5],提出了适用于主动配电网的可靠性综合评估值。该综合评估值既包含了频率、时间、电量的信息和孤岛运行时的电力供求状况,又反映了分布式电源接入对系统的影响。传统可靠性指标有:系统平均停电频率(system average interruption frequency index, SAIFI)、系统平均停电持续时间指标(system average interruption duration index, SAIDI)、系统总电量不足指标(energy not supplied, ENS)和电能质量指标(voltage quality, VOL)。针对分布式电源的新指标包括:DG对SAIDI的贡献系数DSAIDI,DG对SAIFI的贡献系数DSAIFI和孤岛电力不足期望(expected demand not supplied when being island, EDNSI)。
1.1 传统可靠性指标
1)系统平均停电频率指标(SAIFI)
(1)
式中:λi为负荷点i故障率的平均值;Ni为负荷点i的用户数;SAIFI的单位为次/(户·年)。该指标也被定义为用户平均停电次数(average interruption times of customer, AITC)。
2)系统平均停电持续时间指标(SAIDI)
(2)
式中:Ui为负荷点i的年停电时间平均值;SAIDI的单位为小时/(户·年)。该指标还被定义为用户平均停电时间(average interruption hours of customer, AIHC)。
3)系统总电量不足指标(ENS)
ENS=∑LaiUi
(3)
式中,Lai为接入负荷点i的负荷平均值。
4)电能质量指标(VOL)

(4)
式中:(Vr-Vmin)(Vmax-Vr)∑|Pj|表示系统中各个节点在额定电压下的总体电压水平;K为主动配电网中的节点总数;Vi为节点i的电压幅值;Vmax、
Vmin和Vr分别为节点电压上、下限值和额定值;Pi为节点i注入功率;Pj为节点j注入功率。当电压水平越优时,VOL会越高;当节点电压是额定值时,该指标值为最大值为1[3]。
1.2 针对分布式电源的指标
1)DSAIDI为DG对SAIDI的贡献系数,是DG并网后SAIDI的减少量与DG容量之比,计算方法为
(5)
式中:SAIDI0代表DG并网前的系统停电时间平均值;SAIDI1代表DG并网后的系统停电时间平均值;PDG是网络中各个分布式电源的额定容量。
(2)DG对SAIFI的贡献系数DSAIFI,是DG并网后配电网SAIFI的削减值与DG容量的比值。计算公式为

(6)
式中,SAIFI0和SAIFI1分别代表DG并网前后的系统平均停电频率。
3)孤岛电力不足期望
EDNSI=∑(P(t)C(t))
(7)
式中:C(t)为孤岛运行t时刻负荷削减量;P(t)为此刻该事件发生的概率。其中分布式电源出力和负荷削减特性均对C(t)的值有一定影响。
2 序贯蒙特卡洛仿真
序贯蒙特卡洛模拟方法是在固定时段内,按照时间顺序,通过抽样模拟元件的状态转移过程,最终获取系统状态转移的虚拟过程[6]。
为简化计算,对于系统中的元件,只考虑正常运行和故障停运两种状态。抽样的元件考虑了风机、光伏、蓄电池以及线路。一般来说,元件的正常状态持续时间和故障修复时间都服从指数分布,其概率密度函数为
f(t)=λe-λt
(8)
g(t)=μe-μt
(9)
式中:λ为失效率;μ为修复率;f(t)为t时刻发生故障的概率;g(t)为t时刻被修复完成的概率。
对概率密度函数求积分得到概率与时间的关系后,通过产生[0,1]之间的随机数,运用概率密度函数的反函数来确定系统元件的具体工作状态,用于抽样的反函数公式为
(10)
(11)
式中,R1、R2为[0,1]间均匀分布的随机数。对无故障工作时间TTF和失效时间TTR进行图1所示的状态持续时间抽样。

图1 故障与修复状态抽样
通过序贯蒙特卡洛模拟抽样得到各个元件的运行状态后,便可获得整个系统的运行状态,进而对系统的可靠性进行评估。
3 可靠性评估流程
3.1 网络类型分类
在蒙特卡洛仿真过程中,部分线路或者分布式电源可能发生故障,使得配电网络由一个网络裂解成多个网络,形成不同类型的网络区域。所以在进行潮流计算之前,应先对网络区域类型进行分类。网络区域类型可分为3类:第1类为网络中含有电源节点(类型1);第2类为网络中不含有电源节点,但含有PV节点(类型2);第3类为网络中既不含有电源节点,又不含有PV节点(类型3)。
第1类网络可直接按照第3.2节所述的改进的前推回代潮流计算方法进行计算。第3类网络无电源,不需要进行潮流计算。第2类网络需要对参考平衡节点和部分线路进行处理。由于第2类网络中没有电源点,故需要选择一个PV节点作为参考平衡节点,这里以PV节点编号最小的一个节点作为参考平衡节点。当网络正常时,某一线路的始节点和末节点是相对于给定电流正方向而言的,这样便于前推回代潮流计算时确定迭代方向。因此当参考平衡节点改变之后,需要调整部分线路的节点编号。如图2所示,如果电源点0节点发生故障,则该网络将节点6定为参考平衡节点,部分线路始末节点调整如表1所示。因此,对于第2类网络,需要先选定新的参考平衡节点,调整线路的始末节点,然后才可根据第3.2节所述的改进的前推回代潮流计算方法进行潮流计算。
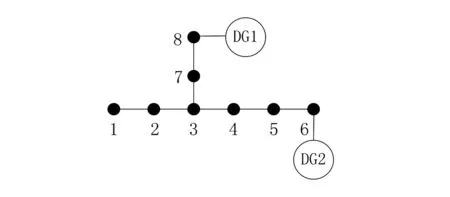
图2 节点编号调整

线路编号故障前始节点末节点故障后始节点末节点2122132332434435455465665
3.2 潮流计算
分布式电源接入配电网,给配电网的功率损耗、电压分布和潮流计算带来了巨大的影响。当分布式电源接入配电网后,潮流的流向也会发生变化,不仅仅是从变电站母线流向负荷的单一方向,也可能会出现回流现象,其电压变化更加复杂,因此有必要对网络中的潮流分布进行进一步分析。
这里将风力发电机和光伏电池等效为PV节点处理;蓄电池等效为PV节点;负荷等效为PQ节点。采用改进的前推回代潮流计算方法,通过无功修正,将有分布式电源接入的PV节点转化为PQ节点进行计算[8]。其计算方法如下:
1)形成PV型分布式电源节点的节点电抗矩阵,并给定无功初始值,将其转化为PQ型节点进行计算。
2)从线路末端开始前推计算系统各个支路的损耗和传输功率,直至前推到始端电源节点。
3)从始端电源节点开始,通过已知首段电压和前推得到的功率,回代计算支路电压降和支路末端电压,直至回代到网络线路最末端。
4)判断收敛情况。对于PQ型节点,连续两次迭代的电压幅值之差小于或等于给定收敛精度即达到收敛。对于PV型节点,本次迭代电压幅值与该PV节点原给定电压幅值之差小于或等于预设精度即为收敛。若收敛,继续下一步;否则,则转至步骤2)。
5)输出潮流计算结果,计算结束。
3.3 潮流平衡调整策略
在潮流计算收敛的前提下,系统可能出现电能富余或者电能缺供的情况,针对不同的情况,需要对蓄电池的出力、风力发电机和光伏系统的出力以及负荷供给进行调整,以使得系统潮流平衡。不同的网络类型有不同的调整策略。类型3中既没有电源节点也没有PV节点,故无需进行调整。类型1和类型2的潮流平衡调整策略如图3和图4所示。
电量富余时,逐步减小蓄电池的出力,每次调整之后检验蓄电池荷电状态约束并重新进行潮流计算,直到电源点的出力符合其出力限制或者所有蓄电池都达到调整下限。当第2类网络(不含电源点,但含有PV节点)系统电量不足时,逐步增加平衡节点之外所有蓄电池出力,最后才调整平衡节点上蓄电池的出力;同样,当系统电量富余时,逐步减小平衡节点之外蓄电池的出力,最后才调整平衡节点上蓄电池的出力,每次调整之后检验蓄电池荷电状态约束并重新进行潮流计算,直到平衡节点的出力符合平衡节点出力限制或者所有蓄电池都达到调整极限。
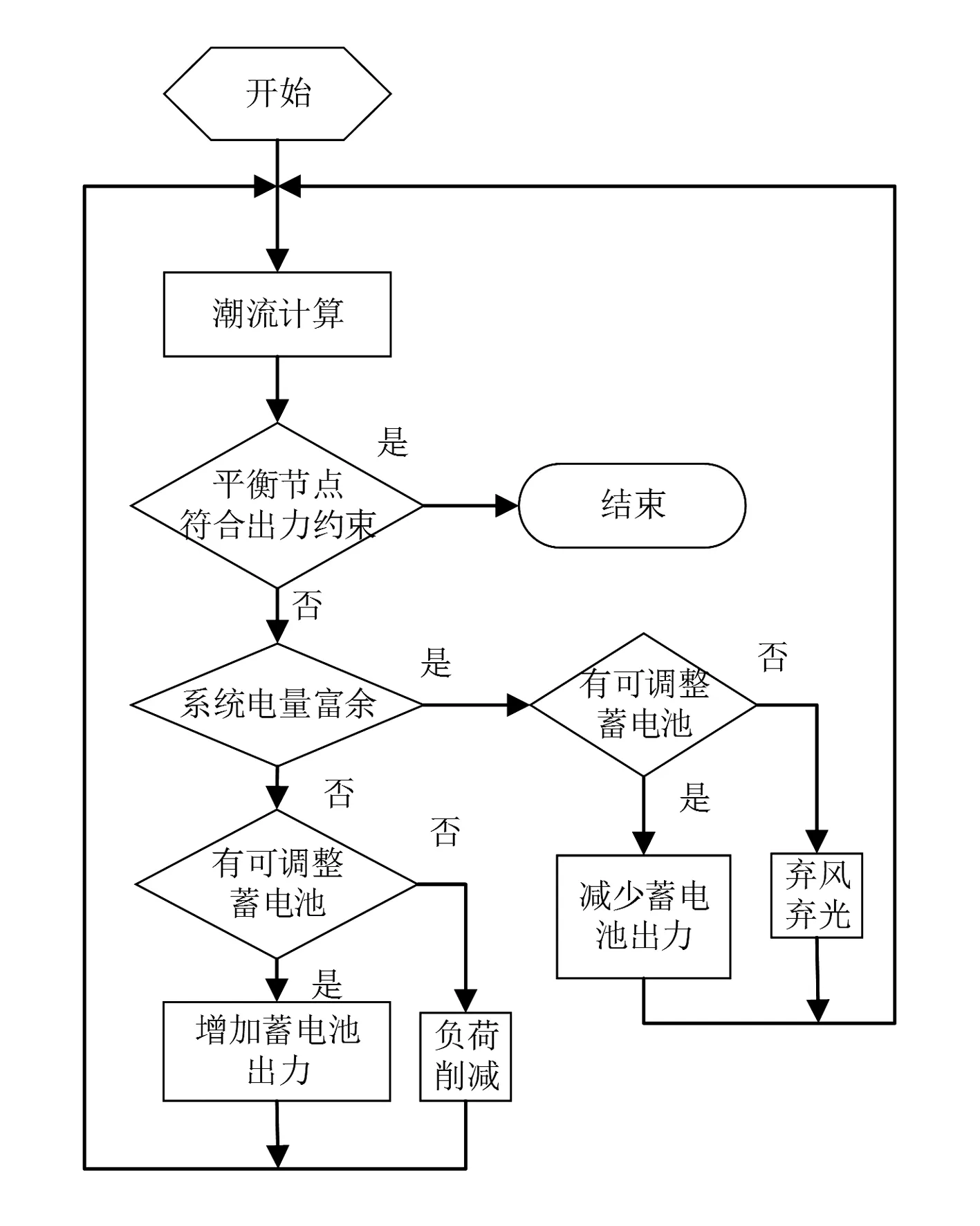
图3 潮流平衡调整(类型1)
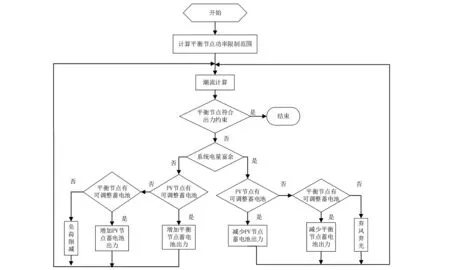
图4 潮流平衡调整(类型2)
2)负荷削减
当系统电力不足,而所有的蓄电池都达到了最大出力时,则需要对负荷进行削减。逐步削减负荷,每次调整之后重新进行潮流计算,直到平衡节点符合出力约束。
3)弃风弃光
当系统电力富余,而所有的蓄电池都达到了最小出力时,则需要减少风力发电机和光伏系统的出力。对于第1类网络(含电源点),应逐步减小所有风力发电机和光伏系统的出力,每次调整后需重新进行潮流计算,直到平衡节点的出力符合出力限制;对于第2类网络(不含电源点,但含有PV节点),先减小平衡节点之外的所有风力发电机和光伏系统的出力,最后才调整平衡节点上的风力发电机和光伏系统的出力,每次调整后都应重新进行潮流计算,直到平衡节点的出力符合出力限制。
3.4 可靠性评估步骤
1)给定初始网络结构、分布式电源安装位置及装机容量、负荷需求量以及线路与分布式电源的故障率、修复率。
2)逐个按时刻进行蒙特卡洛仿真,得到每个时刻的网络结构。
3)对每个时刻的网络进行分析,判断网络断裂成的网络个数,并根据网络类型对网络进行潮流分析。若潮流不平衡,则需根据潮流不平衡调整策略进行调整。
4)根据潮流计算的结果统计计算可靠性指标。
5)基于TOPSIS法和本征向量法计算可靠性综合评估值,再根据综合评估值来评价系统的可靠性高低。
4 算例分析
为验证所提出可靠性评估方法的有效性,以IEEE 33节点为例,对9个方案进行了可靠性评估。
方案1至方案9的网络结构和线路参数均参照IEEE 33节点系统,PQ节点的用户数均为10,其他节点不连接用户。9个方案的分布式电源参数如表2所示。电压上限设置为1.05 p.u.,电压下限设置为0.95 p.u.,线路传输功率限制为7000 kW,线路故障率为0.001,修复率为0.6。蓄电池的初始荷电状态为1。蒙特卡洛总仿真时长设置为8760 h,仿真10次。统计9个方案10次的仿真数据,可靠性综合评估指标如图5所示。
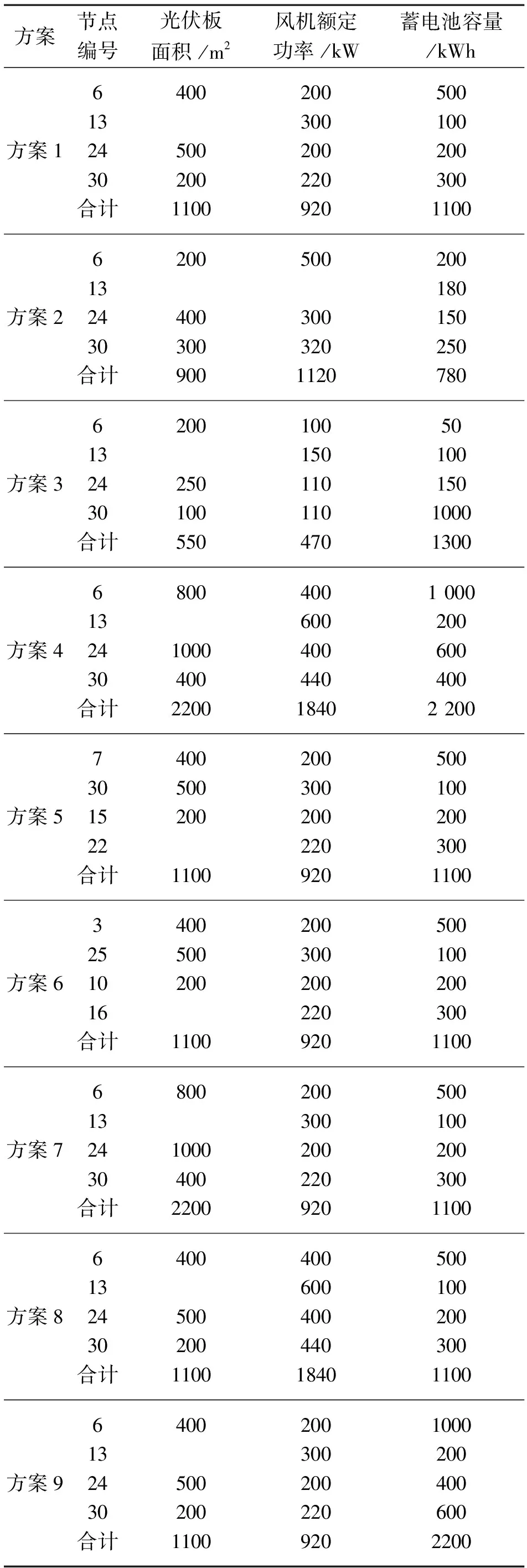
表2 分布式电源参数

图5 可靠性综合评估指标
方案1和方案2的风、光、储的接入位置和装机容量不相同,方案1和方案5、方案6的风、光、储的接入位置不同,但是装机容量相同。在10次试验中,这4个方案的可靠性差异较大,可靠性从大到小排列为方案5、方案1、方案6、方案2,可见,合理设置风、光、储的接入位置和装机容量对于系统的可靠性具有重要意义。
方案3、方案4与方案1的风、光、储的接入位置相同,但方案3的装机容量是方案1的0.5倍,方案4的装机容量是方案1的2倍。在10次试验中,这3个方案可靠性从大到小排列为方案4、方案1、方案3,可见,当风、光、储的接入位置一致时,在一定范围内装机容量越大,系统的可靠性越高。
方案1、方案7、方案8和方案9中,风、光、储的接入位置相同,不同之处在于,方案7光伏系统的装机容量是方案的2倍,方案8风力发电机的装机容量是方案1的2倍,方案9蓄电池的容量是方案1的2倍。通过对比10次试验的结果,4个方案的可靠性相差不大,但方案7和方案8可靠性会略微大于方案1和方案9。综上所述,在一定程度上,风、光、储的装机容量越大,系统可靠性越高。合理选择风、光、储的接入位置可以大大提高系统的可靠性。
5 结 语
为了综合评估主动配电网的可靠性,运用了两类可靠性指标进行评估,即传统可靠性指标和针对分布式电源的可靠性指标。运用序贯蒙特卡洛模拟法确定系统运行状态,从而进一步将网络类型分成3类。应用改进的前退回代潮流计算方法计算网络潮流,并对潮流不平衡进行调整,最终计算系统的综合可靠性指标。随着主动配电网技术的逐步发展,配电网结构将更加复杂,用户侧作为独立的利益主体将更多地参与到配网中来,考虑源—网—荷三方互动的主动配电网可靠性评估是未来重要的研究方向。

