机械工程测试技术课程中的MatLab辅助教学

李云雷 许同乐 王建军 杨小辉

山东理工大学机械工程学院 山东淄博 255000

机械工程测试技术是高等院校机械类各专业的一门专业技术基础课程，具有较强的理论性和实践性，并具有多学科交叉的特点。随着机械工业自动化水平的不断提高，本门课程在机械制造业信息化和创新型人才培养中，发挥着极为重要的作用[1，2]。

1 机械工程测试技术课程教学存在的问题

机械工程测试技术课程在教学过程中存在课程内容多、学时少、理论知识抽象难于理解等问题。该课程主要包括信号描述、测量系统特点分析、传感器技术、模拟信号调理、数字信号处理等内容，且每一部分的教学内容均较多，例如仅传感器技术这部分就有多达十几种传感器。随着大学教学体系的改革，机械工程测试技术的课堂和实验学时均被大幅缩减，无形中增加了任课教师的教学压力[3-5]。

同时，该课程拥有多学科交叉性的属性，学生掌握该课程需要多种学科知识的综合运用，如高等数学、物理学、材料学、电工电子学、计算机等学科知识。这也导致课程中的部分理论知识抽象且难于理解，如信号的频域描述、测量系统的动态特性及不失真测量、信号的相关分析等内容。因此，如何解决内容多、学时少、理论知识抽象等问题成为机械工程测试技术课程教学改革的一项重要任务。

2 MatLab在机械工程测试技术课程的应用

为解决上述问题，将MatLab引入机械工程测试技术的课堂教学，对课程中的部分内容进行仿真分析和演示，将抽象的理论知识具体化，进而提高课堂教学的效率和质量。

MatLab是集数值计算、符号运算及图形处理等功能为一体的科学计算语言。在美国等发达国家的理工科院校中，MatLab已成为一门必修课程。因其在数值分析、自动控制、信号处理、图像处理和仿真等方面的强大功能逐渐成为各学科领域中必不可少的研究工具。在国内，MatLab也已逐步成为理工科的必修课，但在该课程中的应用相对较少。

下面先后使用MatLab软件对周期信号的频谱、二阶系统的失真和不失真测试、信号的相关分析等内容进行仿真演示，以说明该软件在机械工程测试技术课程教学中的作用。

2.1 周期信号频谱结构的分析

信号的频域描述是机械工程测试技术课程教学的首个难点知识。信号的时域表达形式是学生易于理解的，但转换到频域描述后，学生普遍感到抽象难于理解。周期信号的频谱利用傅立叶级数展开获得，教材中详细阐述了傅立叶级数的推导过程，并给出了应用实例。学生仅通过公式推导仍然感到比较模糊，因此利用MatLab软件对周期信号的频域结构进行仿真分析。例如周期三角波信号时域表达式为：

傅立叶级数展开后的表达式为：

依据公式(2)，学生能够理解周期三角波是由不同的谐波组合而成的，但公式表达仍然比较抽象，为此利用MatLab软件仿真分析该周期三角波。如图1所示，第一个波形为直流分量，第二至第五个波形依次为基波、三次谐波、五次谐波和七次谐波，最后的波形为直流和各次谐波的组合，已经非常接近标准的三角波。

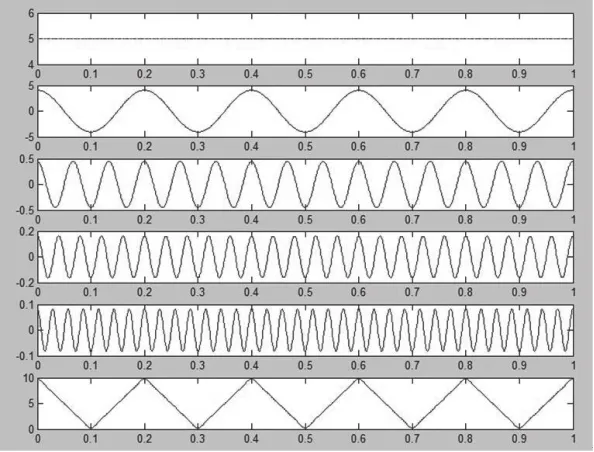
图1 周期三角波的直流、谐波分量及其组合

学生借助MatLab的仿真演示，非常直观地理解了周期三角波由不同的谐波分量组成，每一个谐波就是周期信号的一个频率分量，从而对信号的频域描述也产生了深刻清晰的印象。

2.2 二阶系统的失真和不失真测试

测量系统的动态特性及其不失真测试的条件是该课程的又一个难点知识。以往的课堂教学中反复给学生强调，频率响应函数是频域描述测量系统动态特性的工具，测量系统不失真测试的条件是幅频特性为常数、相频特性是一条直线。但学生却对此充满困惑，为此利用MatLab软件对二阶系统的失真和不失真两种情况进行仿真，如图2和图3所示，并借此为学生释疑。

图2 二阶系统严重失真测试的MatLab仿真

图3 二阶系统近似不失真测试的MatLab仿真

图2和图3中，中间一列是反应二阶系统动态特性的脉冲相应函数和伯德图(频率响应函数的一种表达形式)，左侧是输入信号波形，右侧是输出信号波形。在图2中，输入信号的前三排依次是角频率0.5nω，1nω和22nω的谐波，依据伯德图中的幅频特性曲线，三个谐波对应的输出信号被放大了不同的倍数，这就导致三个谐波的合成信号(第四排左)的输出波形(第四排右)产生严重失真。而在图3中，输入信号依次是角频率0.1nω，0.2nω，0.4nω的谐波和它们的合成信号。由于三个谐波位于0～nω的频率范围内，二阶系统对三者的放大倍数近似相等，因此合成信号的输出波形能够实现近似的不失真。

借助MatLab仿真分析，对比二阶系统失真测试和不失真测试的两种工作状况，学生直观理解了频率响应函数(即伯德图)的物理含义，明晰了测量系统不失真测试的条件。与此同时，可向学生进一步阐明，无论是一阶、二阶系统抑或高阶系统，只要获得其频率响应函数，其动态特性就可全面掌握，从而实现了对知识点的提炼升华。

2.3 信号的相关分析

信号的相关分析这部分内容属于教学课程的最后一章，学时安排少，而知识点涉及概率统计学的内容，学生一般都会产生畏难情绪。但信号的相关分析是机械工程测试技术非常重要的一种手段，要求学生务必掌握该知识点。笔者借助MatLab仿真分析，较好地解决了学时紧张而知识点高难度的问题。

例如，两个随机信号x(t)和y(t)的互相关函数

Rxy(τ)具有同频相关、不同频不相关的特点，课程中也举例作了说明。但仅通过公式表达，学生虽然知道结论，但仍感到抽象。因此利用MatLab仿真，如图4和图5所示。

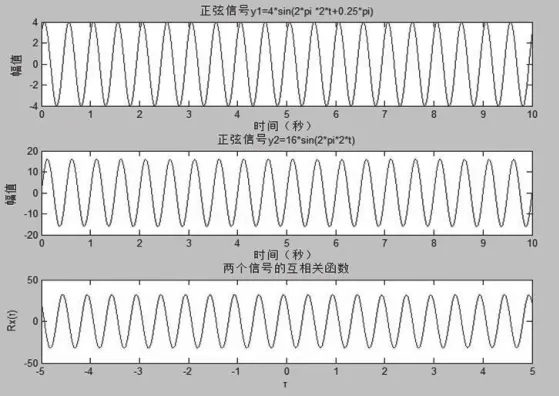
图4 互相关函数同频相关的MatLab仿真

图5 互相关函数不同频不相关的MatLab仿真

在图4中，y1和y2是两个频率相同的正弦信号，二者的互相关函数保留了两个信号的频率信息，具有周期性。在图5中，y1和y2是两个频率不相同的正弦信号，其互相关函数接近于零，即二者不相关。通过图4和图5中MatLab仿真结果的对比分析，学生对教材中公式表达的内容豁然开朗，真正掌握了互相关函数同频相关、不同频不相关的性质，而且印象深刻。

又如，相关滤波是互相关技术的一个典型工程应用。图6是其MatLab的仿真演示，激励信号是正弦波，响应信号是正弦波和噪声两类信号响应的组合，二者的互相关函数非常干净规整，有效过滤掉噪声的干扰。MatLab仿真演示将学生从枯燥的公式推导中解脱出来，轻松掌握相关技术在工程领域的应用，并为将来的工程实践奠定了扎实的理论基础。

图6 相关滤波的MatLab仿真

3 结语

本文将MatLab应用于机械工程测试技术课程的辅助教学，是对传统测试技术教学模式的突破。课堂教学的实践表明，基于MatLab仿真分析和演示，学生易于掌握课程的重点和难点知识，并显著提高了课堂教学效率。同时在教师的指导下，学生借助MatLab软件自己也能轻松实现所有的仿真实例，这也是理论教学和实践教学相结合的一种有益探索。