机器人末端运动特征几何化描述与分析方法

叶梅燕 石志新 罗玉峰,3

(1.南昌大学机电工程学院， 南昌 330031； 2.南昌大学理学院， 南昌 330031；3.华东交通大学机电与车辆工程学院， 南昌 330013)

0 引言

构型综合的前提和关键在于对末端构件运动特征的完整描述和准确分析。末端运动特征既是构型综合的设计目标，又是分析判定所得机构是否符合要求的依据，因此其表达类型的完整性直接决定综合结果的完备性，其分析方法的准确性与难易程度直接关系到综合方法的有效性。

目前已形成4种理论方法：螺旋理论方法[1-6]、位移子群/流形方法[7-11]、方位特征集方法[12-19]和GF集理论方法[20-23]。上述理论方法推动了机器人机构学的迅猛发展，然而仍然存在一些问题：①运动特征信息不完整，机构类型表达不全面。现有运动特征指标中仅含运动类型、运动方向和运动空间维数这3类信息，缺少运动空间整体形态信息。②现有理论方法大多依赖现代代数工具。这些代数方法较为抽象，不易理解，且难以确定运动空间的整体形态，因此有必要提出简单、直观的几何化方法。③矢量线性运算规则不适用于弯曲平移运动特征。方位特征集理论采用矢量描述构件的运动方向，并且利用矢量线性相关性制定了各种运算规则。对于具有弯曲平移特征的机构而言，其移动方向时刻变化，难以采用矢量进行描述，因此相应的矢量线性运算规则不再适用。

本文提出基于高斯几何学的几何化描述与分析方法。首先借鉴高斯几何学将直线、曲线、平面以及曲面等均视作可描述末端运动特征的独立空间，进而建立基于高斯几何学的运动特征描述模型；然后基于该描述模型制定末端运动特征的求并和求交运算规则；最后结合实例提出机器人末端运动特征的分析方法。

1 末端构件运动特征的描述方法

机器人末端构件的运动属于刚体运动，它包括平移运动(简称移动)和旋转运动(简称转动)2种运动类型。因此机器人末端构件的运动特征应由转动特征和移动特征共同组成，即

(1)

式中M——末端构件运动特征集

TC——末端构件移动特征

RC——末端构件转动特征

1.1 移动特征

为了清晰描述机器人末端构件的移动特征，给出如下定义：

定义1：末端构件作平移运动(姿态保持不变)时，构件上任意一点的轨迹均相同，该轨迹称为末端构件的移动空间(记为T)。

值得注意的是，移动空间包括平直空间(即轨迹为直线或平面)和弯曲空间(即轨迹为曲线或曲面)2种情况。如平行四边形机构中连杆作圆周曲线平移运动，连杆上任意一点的轨迹均为圆周曲线，因此其移动空间为弯曲空间。

对于平直空间而言，其维数和基向量可直接反映独立移动数目及方向。然而由于弯曲空间不存在基向量，因此除了维数外，还应给出其整体形态和生成方式等信息。考虑到平直空间属于弯曲空间的特例，采用统一模型来描述移动特征，其形式为

TC=tp(T)=tp(w,N)

(2)

式中t——移动

p——移动空间维数

w——移动空间整体形态

N——移动空间生成方式

值得注意的是：①基于高斯几何学的基本思想，直线和曲线被视为1维独立空间，平面和曲面被视为2维独立空间。②0维和3维移动空间无需记录整体形态和生成方式，因此其移动特征可分别表示为t0和t3。

1.2 转动特征

旋转运动可利用旋转轴进行刻画，因此旋转轴的数目和方向可反映机器人末端构件的转动特征。为了清晰描述转动特征，给出如下定义：

定义2：末端构件所有允许的旋转方向单位矢量的集合称为转动特征集(记为S)。

根据定义2不难发现，转动特征集中向量的个数和向量的方向可直接分别反映旋转轴的数目和方向。因此转动特征可表示为

RC=rq(S)

(3)

式中r——转动

S——转动特征集

q——转动特征集维数

转动特征集表示方法包括：①0维转动特征集表示末端构件不存在任何方向的旋转运动，故转动特征可表示为r0。②1维转动特征集可表示为r1(l)，其中l为1维转动轴线方向单位矢量。③ 2维转动特征集可表示为r2(l1,l2)，其中l1和l2为转动轴线方向单位矢量。④ 3维转动特征集表示末端构件可绕任意方向作旋转运动，因此转动特征可表示为r3。

2 串联机构末端构件的运动特征

由于串联机构是由若干个运动副依次串联而成，因此串联机构末端构件的运动特征集是各运动副运动输出特征的并集，即可表示为

(4)

式中Ms——串联机构的运动特征集

Mi——第i个运动副的输出特征

2.1 单个运动副的运动输出特征

机器人机构的运动副类型较多，常见运动副包括：转动副、移动副、球副、胡克铰、圆柱副等。为了分析方便，可采运动副等效替换的方法将它们简化为只含转动副和移动副2种。例如，球副等效为3个轴线汇交于1点的转动副，胡克铰等效为2个轴线垂直正交的转动副，圆柱副等效为共轴的转动副和移动副。

(1)移动副(P副)的运动输出特征。由于P副仅产生直线平移运动，其移动空间整体形态为直线，并且该移动空间由P副生成，因此根据式(2)可知，移动副的运动输出特征可表示为t1(直线,P)，其中P为P副的方向矢量。

(2)转动副(R副)的运动输出特征。转动副不仅能产生绕其轴线的运动，而且可衍生出垂直于轴线方向的圆周曲线平移运动，即其运动特征具有二重性。可按如下规则选取：①优先取旋转运动作为运动输出特征，记为r1(R)，其中R为R副轴线方向矢量。②若已有运动副产生了与该转动副旋转方向相同的旋转运动，则该转动副将会衍生圆周曲线平移(图1)，此时应取衍生圆周曲线平移作为其运动输出特征，记为t1(圆,R)。

图1 R‖R机构的移动空间Fig.1 Structure diagrams of R‖R mechanism

2.2 运动特征求并运算规则

2.2.1转动特征的求并运算规则

根据定义1可知，转动特征是方向矢量的集合，因此转动特征RC可利用矢量线性相关性进行分析确定，具体运算规则如下。

(1)r0与r1的求并运算规则

r0∪r1(R)=r1(R)

(2)r1与r1的求并运算规则

当R1‖R2时，r1(R1)∪r1(R2)=r1(R1)，否则求并结果为r2(R1,R2)。

(3)r2与r1的求并运算规则

当R3可由向量组(R1,R2)线性表示时，r2(R1,R2)∪r1(R3)=r2(R1,R2)，否则求并结果为r3。

(4)r3与r1的求并运算规则

r3∪r1(R)=r3

2.2.2移动特征的求并运算规则

移动特征求并运算共存在如下4条规则：

(1)t0与t1的求并运算规则

t0∪t1(w,N)=t1(w,N)

(2)t1与t1的求并运算规则

按移动空间类型划分，存在如下3种情况：

①t1(直线,P1)∪t1(直线,P2)。若P1‖P2则TC=t1(直线,P1)，否则TC=t2(平面,n)，其中n为该平面的法向量。

②t1(直线,P)∪t1(圆,R)。考虑直线和圆所在平面全部可能的方位关系及布置顺序，其移动特征TC存在3种情况，具体包括：t2(平面,R)、t2(圆柱面,P+R)和t2(圆锥面,P+R)，其中P+R表示该移动空间由P副和R副产生的平移经运动合成而成(下同)。其详细求并结果和相应示例如表1所示。

假定孤石为完整块体，内部无节理裂隙，只考虑重力作用，孤石相对于周围残积土刚度足够大，相互作用过程中可以不考虑变形作用，与孤石接触的周围土体，为均质、各向同性体，不考虑作用过程中土体各向异性和非线性作用对孤石与土体相互作用的影响。孤石重力作用的稳定计算考虑叠石、完全出露、部分出露、完全埋入4种情况。

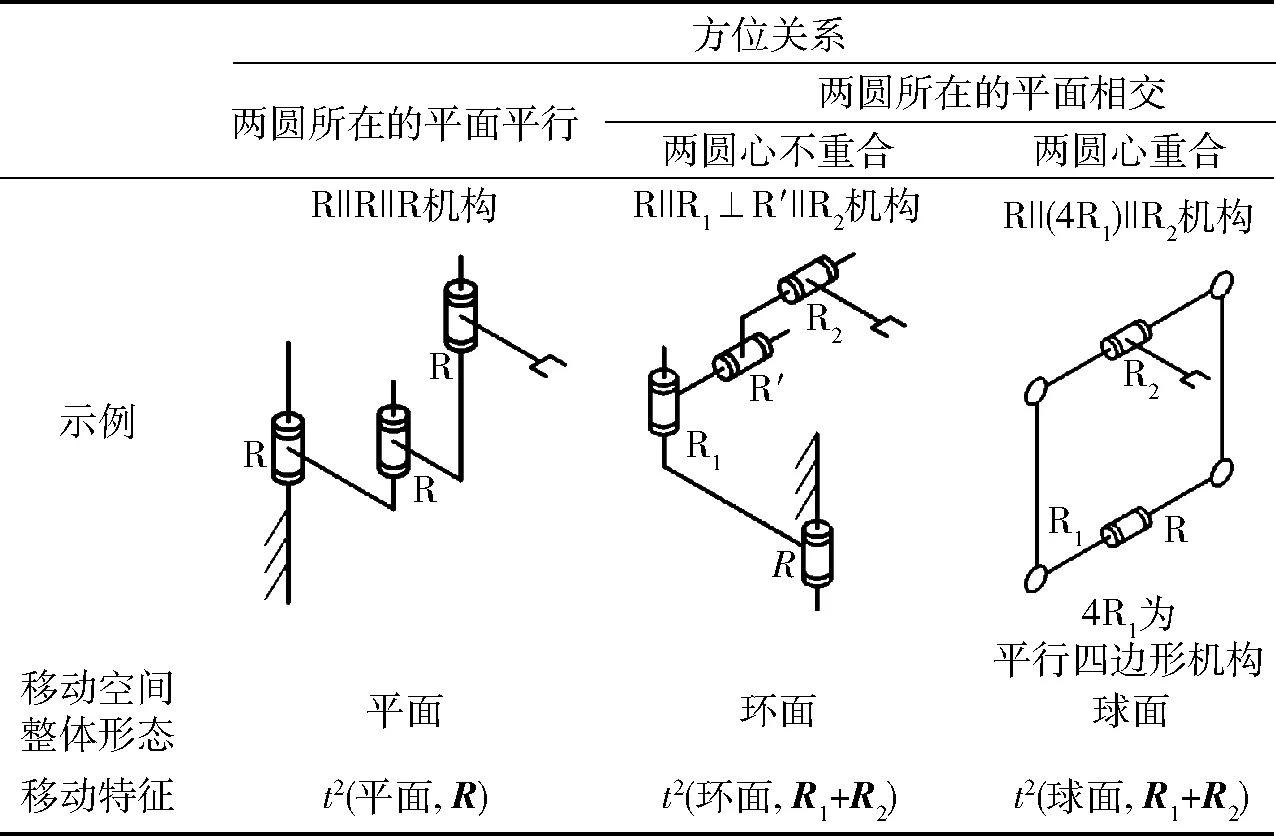
③t1(圆,R1)∪t1(圆,R2)。考虑两圆所在平面的全部可能方位关系，其移动特征TC存在3种情况，具体包括：t2(平面,R1)、t2(环面,R1+R2)和t2(球面,R1+R2)。其详细求并结果和相应示例如表2所示。

表1和表2中部分示例机构的移动空间如图2所示。

(3)t2与t1的求并运算规则

一般而言，t2与t1的求并结果为t3，但存在3种特殊情况：

①t2(平面,n)∪t1(直线,P)。若P⊥n则移动特征TC=t2(平面,n)，否则TC=t3。

②t2(平面,n)∪t1(圆,R)。若R‖n则移动特征TC=t2(平面,n)，否则TC=t3。

③t2(圆柱面,P1+R)∪t1(直线,P2)。若P1‖P2则TC=t2(圆柱面,P1+R)，否则TC=t3。

t3∪t1(w,N)=t3

2.3 串联机构运动特征分析方法及实例

2.3.1串联机构运动特征分析方法

串联机构运动特征分析方法和步骤如下：

(1)赋初值。将转动特征集和移动特征集的初值均赋为空集，即RC=r0，TC=t0。

(2)确定运动副的运动输出特征。①当第i个

表1直线平移和圆周平移的求并运算规则
Tab.1Unionoperationrulesoflinetranslationandcirculartranslation

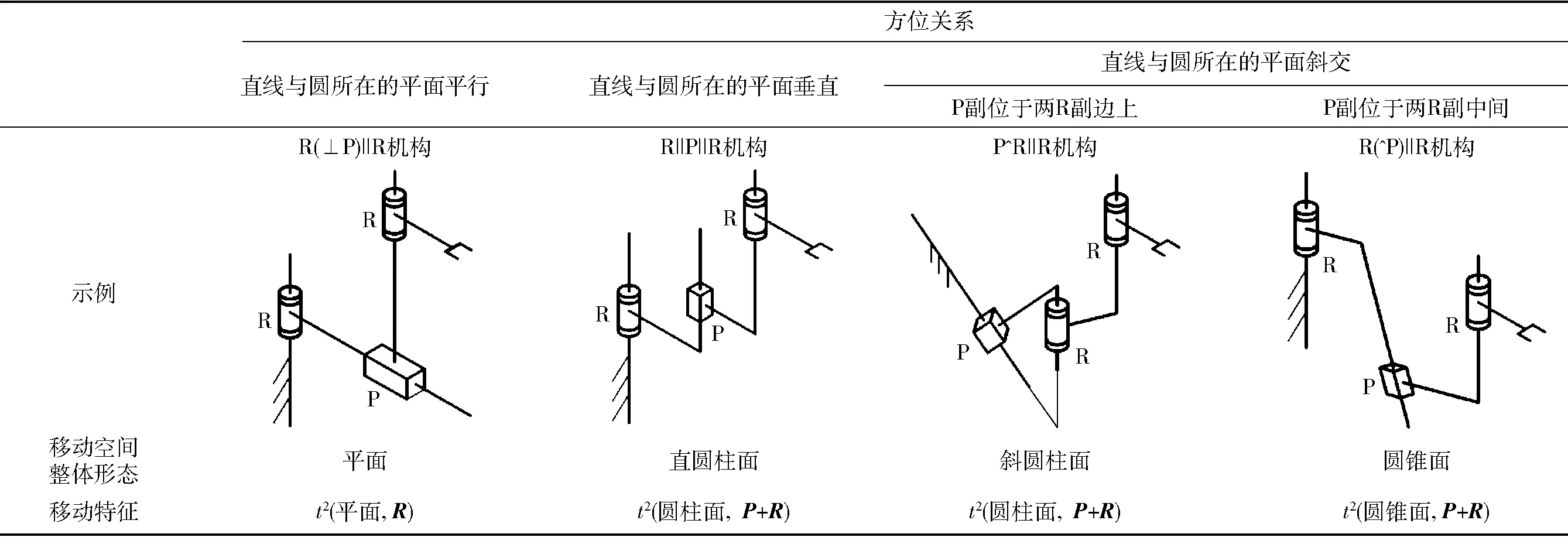
表2 两圆周平移经求并运算后的移动特征Tab.2 Union operation rules of two circular translation

运动副为移动副Pi时，其运动输出特征唯一，并且运动输出特征为t1(直线,Pi)。②当第i个运动副为转动副Ri时，优先取其旋转运动作为运动输出特征，判断矢量Ri能否由转动特征集S中的向量线性表示，若否，则取其运动输出特征为r1(Ri)；若是，则取其衍生平移运动t1(圆,Ri)作为运动输出特征。

(3)运动特征集的更新。根据2.2节介绍的求并运算规则，更新运动特征集。

(4)循环。从i=1开始，重复步骤(2)和(3)，直到i=n终止，其中n为经运动副等效替换后机构所有运动副数目之和。

(5)结束。输出最终的转动特征RC和移动特征TC，得到末端构件运动特征集M。

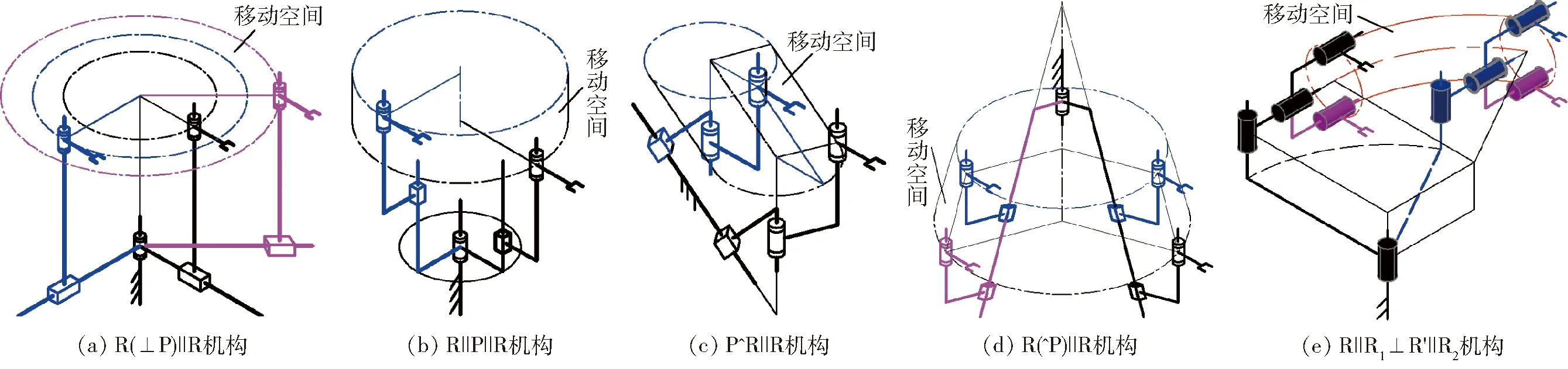
图2 表1和表2中部分机构的移动空间Fig.2 Translation spaces of some mechanisms in Tab.1 and Tab.2

2.3.2实例分析

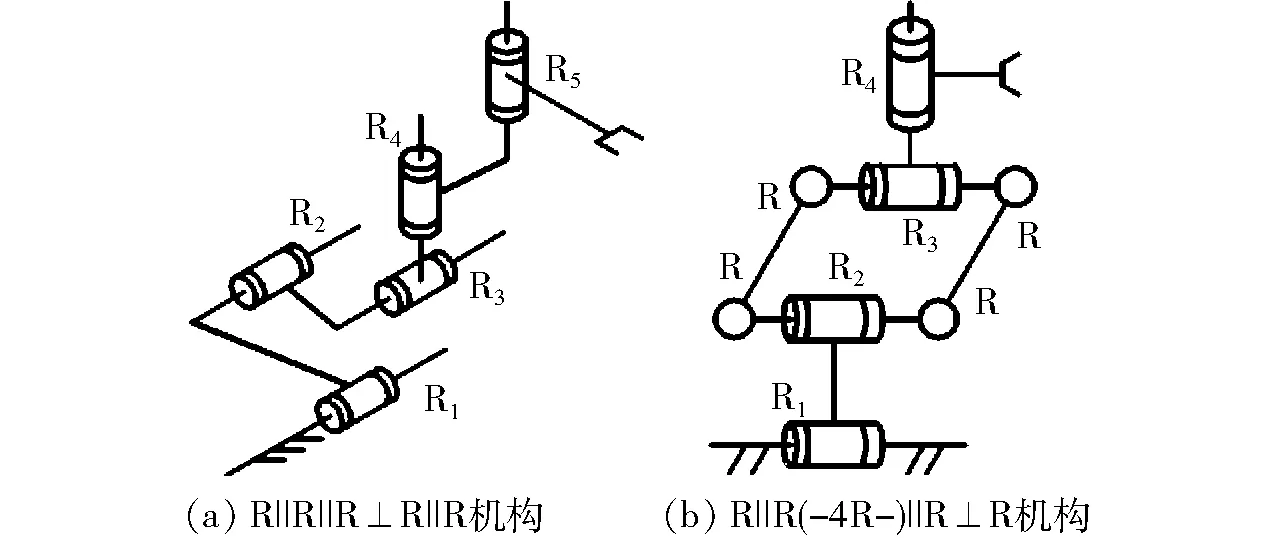
图3 机构简图(例1)Fig.3 Structure diagrams of example 1

例1：利用上述运动特征分析方法，分析图3串联机构末端构件的运动特征。

根据上述串联机构运动特征分析方法，图3a机构运动特征分析步骤及结果如下：

(1)赋初值

RC=r0TC=t0

(2)确定运动副的运动输出特征

当i=1时，第1个运动副为转动副R1，此时转动特征集RC=r0，转动特征集S为空集，故方向矢量R1不能被S中的向量线性表示，因此转动副R1的运动输出特征为r1(R1)。

(3)运动特征集的更新

由转动特征求并运算规则(1)可知，转动特征集RC=r0∪r1(R1)=r1(R1)，移动特征集TC保持上步结果t0不变。

(4)循环(重复步骤(2)和(3))

当i=2时，第2个运动副为R2，由于R2‖R1，故R2能被R1线性表示，因此R2的运动输出特征取为衍生平移运动t1(圆,R2)。由移动特征求并运算规则(1)可知：TC=t0∪t1(圆,R2)=t1(圆,R2)。RC保持上步结果r1(R1)不变。

当i=3时，第3个运动副为R3，由于R3‖R1，故其运动输出特征取为t1(圆,R3)。由于R2‖R3，根据移动特征求并运算规则(2)中的情况③可知：TC=t1(圆,R2)∪t1(圆,R3)=t2(平面,R2)。RC保持上步结果r1(R1)不变。

当i=4时，第4个运动副为转动副R4。由于R4与R1不平行，R4不能被R1线性表示，故其运动输出特征取为r1(R4)，因此根据转动特征求并运算规则(2)可知RC=r1(R1)∪r1(R4)=r2(R1,R4)。TC保持上步结果t2(平面,R2)不变。

当i=5时，第5个运动副为转动副R5。由于R5‖R4，故R5能被向量组(R1,R4)线性表示，因此其运动输出特征取为t1(圆,R5)。由于R2与R5不平行，依移动特征求并运算规则(3)中的情况②可知：TC=t2(平面,R2)∪t1(圆,R5)=t3。RC保持上步结果r2(R1,R4)不变。

(5)输出末端构件运动特征集M

(5)

图3b机构运动特征主要分析步骤及结果如下：首先，容易分析得到R1‖R2‖R3的转动特征和移动特征分别为r1(R1)和t2(平面,R2)。其次，不难判定平行四边形机构(4R)和运动副R4的运动输出特征分别为t1(圆,R)和r1(R4)。最后，依求并运算规则可知：该机构移动特征集为TC=t2(平面,R2)∪t1(圆,R)=t3，转动特征集为RC=r1(R1)∪r1(R4)=r2(R1,R4)。因此该机构末端构件运动特征集亦为式(5)。

3 并联机构动平台的运动特征

3.1 并联机构动平台运动特征的分析方法

由于动平台是在各支链共同作用下进行运动，因此并联机器人机构动平台的运动特征是各支链末端运动特征的交集。

3.1.1动平台转动特征的分析方法

根据定义2可知，转动特征集是转动轴线方向单位向量的集合，因此分析并联机构动平台转动特征的问题，可转化为确定各支链转动特征集的公共向量问题，具体分析方法如下：

设并联机构有m条支链组成，各支链转动特征集及其维数分别记为Sj和qj，其中j=1, 2,…,m,则并联机构动平台的转动特征RC可表示为

(6)

由于式(6)中m个转动特征集均为单位向量的集合，因此由线性代数知识不难确定它们的公共向量(记为S)，进而得公共向量S的维数q，从而得到并联机构动平台的转动特征。

3.1.2各支链末端移动特征的求交运算规则

根据定义1可知，移动空间不属于线性空间，不能利用线性相关性得到求交运算结果。由于各支链移动空间的整体形态特征已知，因此可采用几何方法分析确定出求交运算结果。

(1)t0与其他移动特征的求交运算规则

t0∩tp(w,N)=t0

(2)t1与t1的求交运算规则

按移动空间类型划分，存在如下3种情况：

①t1(直线,P1)∩t1(直线,P2)。空间两直线的位置关系存在平行、相交和交叉3种情况。当且仅当两直线相互平行时，二者交集为一段连续的位移空间，故P1‖P2时TC=t1(直线,P1)，否则TC=t0。

②t1(直线,P)∩t1(圆,R)。由于直线和圆的交集不是一段连续的位移空间，因此TC=t0。

③t1(圆,R1)∩t1(圆,R2)。如表3所示，二者的求交结果一般为t0，但存在如下特殊情况：当两圆所在平面平行，两圆大小相等，且机构末端构件分别联接在两圆的对应位置点上时，二者的求交结果为TC=t1(圆,R1)。

表3两圆周平移的求交运算规则
Tab.3Intersectionoperationrulesoftwocirculartranslation

值得注意的是，两圆大小相等需要由构件的尺寸保证，但在进行机构拓扑结构分析与综合时，一般不考虑构件的具体尺寸，因此本文后续求交运算规则中均不考虑构件尺寸对机构末端运动特征的影响，即默认各支链移动空间的大小不相等。

(3)t1与t2的求交运算规则

按移动空间类型划分，存在如下7种情况：

①t1(直线,P)∩t2(平面,n)。当且仅当直线和平面平行(即P⊥n)时，二者交集为一段连续的位移空间，求交结果为TC=t1(直线,P)，否则TC=t0。

②t1(直线,P1)∩t2(圆柱面,P2+R)。当且仅当直线和圆柱面的素线平行(即P1‖P2)时，求交结果为TC=t1(直线,P1)，否则TC=t0。

③t1(直线,P1)∩t2(圆锥面,P2+R)。当且仅当直线和圆锥面的素线平行(即P1‖P2)时，二者交集TC=t1(直线,P1)，否则TC=t0。

④t1(直线,P)∩t2(环面,R1+R2)。由几何知识可知直线和环面的交集不是一段连续的位移空间，因此二者求交结果为TC=t0。

⑤t1(直线,P)∩t2(球面,R1+R2)。由于直线和球面的交集不是一段连续的位移空间，因此二者求交结果为TC=t0。

⑥t1(圆,R)∩t2(平面,n)。当且仅当圆周所在平面和平面平行(即R‖n)时，二者交集为一段连续的位移空间，求交结果为TC=t1(圆,R)，否则TC=t0。

⑦不考虑构件的具体尺寸，即默认各支链移动空间的大小不相等时，圆周与圆柱面、圆锥面、环面以及球面的交集都不是一段连续的位移空间，因此t1(圆,R)与t2(圆柱面,P+R)，t2(圆锥面,P+R)，t2(环面,R1+R2)以及t2(球面,R1+R2)的求交结果均为TC=t0。

(4)t2与t2的求交运算规则

由于2维移动空间的整体形态包括平面和曲面(圆柱面、圆锥面、环面、球面)2种类型，因此存在如下3种情况：

①t2(平面,n1)∩t2(平面,n2)。当n1‖n2时二者求交结果为TC=t2(平面,n1)；否则求交结果为TC=t1(直线,n1×n2)。

②平面和曲面求交。可知，平面和曲面的交集为截交线。截交线形状包括椭圆、圆、抛物线、双曲线等，但它们均为平面曲线。因此这类移动空间均为1维平面曲线，其整体形态均可称为截交线。例如，2维移动特征t2(平面,n)与t2(圆柱面,P+R)的求交结果可表示为TC=t1(截交线,n)。

③曲面和曲面求交。可知，曲面和曲面的交集为相贯线。相贯线属于空间曲线。因此这类移动空间为1维空间曲线，其整体形态可统称为相贯线。例如，2维移动特征t2(圆柱面,P1+R1)与t2(圆锥面,P2+R2)的求交结果可表示为TC=t1(相贯线,(P1+R1)∩(P2+R2))。

(5)t3与其他移动特征的求交运算规则

t3∩tp(w,N)=tp(w,N)

3.2 实例分析

例2：分析确定图4a[15]和图4b[17]并联机构的动平台运动特征集。

图4 机构简图(例2)Fig.4 Structure diagrams of example 2

图4a所示机构由4条支链组成，并且支链Ⅰ和Ⅱ的结构特征均为R‖R‖R⊥R‖R；支链Ⅲ和Ⅳ的结构特征均为R-S-S。联接在静平台上的4个转动副方位特征为R11‖R31‖R41⊥R21；联接在动平台上的2个转动副方位特征为R15‖R25。该机构动平台运动特征分析步骤及结果如下：

由例1可知，支链Ⅰ和Ⅱ的移动特征均为t3；转动特征分别为r2(R11,R14)和r2(R21,R24)。将支链Ⅲ和Ⅳ中的球副等效为轴线汇交于1点的3个转动副后，利用上述串联机构运动特征分析方法不难发现，二者的移动特征和转动特征分别为t3和r3。

根据3.1节介绍的运动特征求交运算规则，动平台的移动特征为TC=t3∩t3∩t3∩t3=t3。由于R14‖R15‖R25‖R24但R11⊥R21，故向量组(R11,R14)和(R21,R24)的公共向量为R14，因此转动特征为RC=r2(R11,R14)∩r2(R21,R24)∩r3∩r3=r1(R14)。图4a所示机构的动平台运动特征集M为

(7)

式(7)表明，该机构的动平台具有在3维平移以及绕R14方向旋转的运动输出能力。这与文献[15]分析结果一致。

图4b所示机构由4条相同支链组成，其结构特征均为R‖R(-4R-)‖R⊥R。联接在静平台上的4个转动副的方位特征为R11‖R31⊥R21‖R41；联接在动平台上的4个转动副的方位特征为R14‖R24‖R34‖R44。该机构动平台运动特征分析步骤及结果如下：

由例1可知，4条支链的移动特征均为t3，转动特征为r2(Ri1,Ri4)，i=1,2,3,4。

由于R14‖R15‖R25‖R24但R11‖R31⊥R21‖R41，故向量组(R11,R14)、(R21,R24)、(R31,R34)、(R41,R44)的公共向量为R14。根据3.1节介绍的运动特征求交运算规则，该机构动平台的移动特征TC和转动特征RC为

(8)

式(8)表明，该机构动平台具有在3维平移以及绕R14方向旋转的运动输出能力。这与文献[17]分析结果一致。

例3：分析确定图5所示并联机器人机构动平台的运动特征。

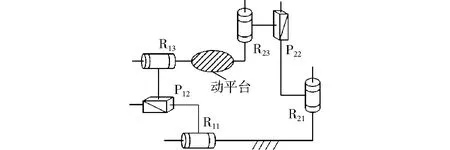
图5 机构简图(例3)Fig.5 Structure diagram of example 3

图5所示机构由2条支链组成，支链1的结构特征为R11‖P12‖R13，支链2的结构特征为R21‖P22‖R23。

利用串联机构运动特征分析方法可得：支链1的转动特征和移动特征分别为r1(R11)和t2(圆柱面,P12+R13)；支链2的转动特征和移动特征分别为r1(R21)和t2(圆柱面,P22+R23)。

由3.1节的支链运动特征求交运算规则可得：由于R11和R21不平行，故动平台的转动特征RC=r1(R11)∩r1(R21)=r0，移动特征TC为t1(相贯线,(P12+R13)∩(P22+R23))。因此图5所示机构动平台的运动特征集M为

(9)

式(9)表明，该机构的动平台仅能沿两圆柱面的相贯线作平移运动。

例4：分析确定图6所示并联机器人机构动平台的运动特征。

图6 机构简图(例4)Fig.6 Structure diagram of example 4

图6所示机构由3条支链组成。支链1的结构特征为R11‖P12‖R13‖R14，支链2的结构特征为R21‖P22‖R23，支链3由4个运动副依次串联，结构特征为P31‖R32‖R33‖R34，并且各支链联接在机架上的3个运动副满足R11‖R21‖P31。

利用串联机构运动特征分析方法可得：支链1的转动特征和移动特征分别为r1(R11)和t3；支链2的转动特征和移动特征分别为r1(R21)和t2(圆柱面,P22+R23)；支链3的转动特征和移动特征分别为r1(R32)和t3。

由于R11‖R21‖P31‖R32，故其转动特征RC为r1(R11)∩r1(R21)∩r1(R32)=r1(R11)，移动特征TC为t3∩t2(圆柱面,P22+R23)∩t3=t2(圆柱面,P22+R23)。图6所示机构动平台的运动特征集M为

(10)

式(10)表明，该机构的动平台具有在2维空间(整体形态为圆柱面)上平移以及绕R11方向旋转的运动输出能力。

4 结论

(1)提出的基于高斯几何学的描述方法可以准确、完整地描述机器人末端构件的运动特征。

(2)运动空间整体形态是运动特征的重要信息之一，根据运动空间整体形态对机构类型作进一步细分，有利于丰富和完善现有机构类型库。

(3)与代数方法相比，机器人末端运动特征几何化分析方法具有简单、直观等优点。对于具有弯曲移动特征的机构而言，该方法的优势更为显著。