基于区间两阶段鲁棒优化模型的灌区水资源优化配置

陈红光 王琼雅 李晓宁 王中君 李晨阳

(1.东北农业大学水利与建筑学院， 哈尔滨 150030； 2.东北农业大学工程学院， 哈尔滨 150030)

0 引言

随着社会经济和人口的快速增长，水资源短缺问题日益突出。随着粮食需求不断增加，农业作为用水大户，水资源供需问题不断加重[1-2]。合理配置农业用水、提高农业用水效率对缓解水资源供需矛盾和用水压力具有十分重要的意义[3-5]。灌区作为农业用水主体，其水资源的合理优化配置对提高水资源利用率、促进农业水资源的可持续开发利用、权衡灌区水资源经济和风险之间的关系具有重要作用。

近年来，水资源优化配置得到了广泛发展，出现了多种优化配置方法。娄帅等[6]基于免疫遗传算法构建多阶段群决策优化模型，解决漳河流域水资源优化配置问题。孙冬营等[7]运用模糊联盟合作博弈方法将水资源进行两次分配，得到流域水资源的合理配置方案。陈述等[8]将粒子群人工蜂群算法运用到灌区渠-塘-田的水资源优化配置中。上述研究基于确定的水资源系统进行配置，但在实际中，灌区灌溉系统受到气象条件、作物需水量以及政策变化等因素影响，是一个复杂的动态配水系统[9]。传统方法在处理系统中的不确定因素时，存在一定的局限性。因此，为了解决这些包含不确定因素的问题，提出了不确定优化方法，其中两阶段随机规划模型得到了广泛应用[10]。HUANG等[11]将不确定性优化和两阶段随机规划方法应用到水资源系统管理中；LI等[12]将区间两阶段机会约束模型运用到水资源规划中；ZHANG等[13-14]运用改进后的区间两阶段随机规划算法，对三江平原水资源进行优化配置。区间两阶段优化算法在大量学者[15-17]的努力下，逐渐得到完善，用以处理水资源配置过程中的不确定性问题。区间两阶段随机效用模型处理不确定因素十分有效，但却忽略了系统风险问题，模型结果不具有绝对可行性。而鲁棒优化方法则能够在规划过程中对风险进行有效规避，并权衡系统中可变随机值和追索成本的关系[18-20]。

本文针对灌区水资源配置模型中存在风险的特点，构建多水源、多作物配水模型，以两阶段线性规划为基础，建立区间两阶段鲁棒优化模型(Interval-parameter two-stage robust stochastic programming model，ITRM)，采用概率密度函数、离散区间表示系统的不确定性，用鲁棒系数表示系统的风险。在不同来水情况下，对各个灌区的不同作物进行水资源的优化配置，以期为灌区管理者提供风险可控、成本最优的配水方案。

1 模型建立与求解

1.1 模型建立

灌区多水源优化配置是一个复杂的系统过程，供水情况受来水量等因素影响，存在一定的随机特点[21]。且多水源联合优化调度目的是使水资源得到合理的分配，满足灌区用水需求，同时尽量减少用水成本。因此，本文以灌区农作物需水量为决策变量，引入用水成本、缺水惩罚系数，并分两个阶段确定灌区水资源的最优配置。在保证灌区水资源承载力的前提下，以正常水平年作物需水量为依据，确定作物预先配水目标，并将其作为第1阶段的决策变量；由于受灌区初始储水量、天然来水量、水源蒸发量等因素的影响，供水量可能小于供水目标，这就需要决策者进行调整，减少灌区供水量或者外调水源进行补水，而减少供水量会影响作物产量，外调水源则会增加用水成本，都会产生经济惩罚，为降低用水成本，需要对第1阶段的配水量进行调整，将缺水量作为第2阶段的决策因素。故两阶段随机规划模型为

(1)

式中Cij——水源i向作物j的输水成本，元/m3

Wij——水源i向作物j的预先目标配水量，m3

E——随机变量的期望值

Dij——水源i未满足作物j预先目标配水量时的缺水惩罚系数，元/m3

Sij——水源i未满足作物j预先目标配水量时的缺水量，m3

i——水源，i为1、2分别表示地表水和地下水

j——作物，j为1、2、3分别表示水稻、玉米、大豆

f——系统总成本，元

(2)

式中Sijh——来水量水平为h时，i水源向j作物供水，未满足预先目标配水量的缺水量，m3

已有的研究较少考虑系统风险问题，无法保证模型最优解的绝对可行性。鲁棒优化方法将风险体现在函数当中，对风险进行有效测评，并在规划过程中规避风险，平衡系统的成本和风险的关系，可以有效增加模型求解的可行性和系统的稳定性[22]。因此，本文在两阶段随机规划模型的基础上引入鲁棒优化方法，建立两阶段随机鲁棒优化模型。模型表述为

(3)

式中ρ——鲁棒系数

(4)

式中θih——松弛变量

θih主要作用是保证模型的稳定性和非负性。作物预先目标配水量(需水量)Wij具有不确定性，且作物的价格和产量变动导致惩罚系数Dij也不确定。为表示不确定性，引入区间参数来表示不确定性参数。“+”表示参数的上限，“-”表示参数的下限，建立区间两阶段鲁棒优化模型(ITRM)

(5)

(1)需水量约束

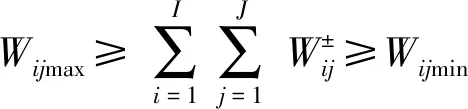
(6)

式中Wijmax——作物j正常生长的最大需水量

Wijmin——作物j正常生长的最小需水量

(2)水源可用水量约束

地表水约束为

(7)

地下水约束为

(8)

式中Qij——灌区初期水源i的储水量，m3

Qim——灌区末期水源i的蓄水量，m3

不错，《罕哈冉惠传》中出现了不少反映佛教思想的内容。如学者们指出的，当哈冉惠和他的两个兄弟遭蟒古斯暗害，误食了蟒古斯投下的毒药后，哈冉惠变成了长有九十五颗头的大黑蟒古斯，他的胞弟乌兰岱·莫日根变成了一尊石人，乌兰岱的坐骑变成了一尊石马，他的义兄弟吉尔吉斯·赛因·贝托尔则变成了一头黄色的野猪。是两位公主派出了维兰·索龙嘎的儿子去向菩萨求救，菩萨将三件宝物——万能的金套绳、能起死回生的仙丹、智慧的金盘赐给了小童，小童用此三宝使三位英雄得救，恢复了原貌。菩萨，为众人所知，当然属于重要的佛的形象，然而当菩萨向小童授予三件宝物之前，却说出下面一段颇令人费解的话：

qih——水源i的来水量，m3

Qsi——灌区水源i的蒸发量，m3

Qimin——水源i最低蓄水量，m3

(3)追索变量约束

追索变量约束为

(9)

(4)水源最大供水量约束

水源最大供水量约束为

(10)

式中Wimax——水源i最大可供水量，m3

(5)非负约束

非负约束为

(11)

1.2 模型求解

将ITRM分为两个子模型进行求解，对应的目标函数下限子模型为

(12)

约束条件为

(13)

(14)

约束条件为

(15)

(16)

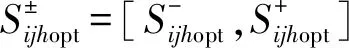
(17)

zij=zijopt(∀i,j)

(18)

最优配水量为

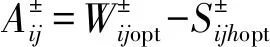
(19)

式中Aij——水源i向作物j的最优配水量

其算法流程如图1所示。

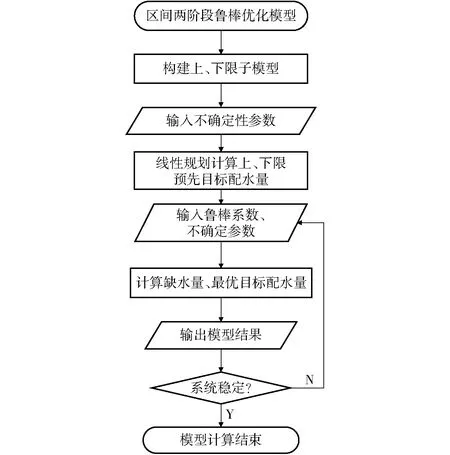
图1 区间两阶段鲁棒优化方法算法流程图Fig.1 Algorithm flow chart of interval-parameter two-stage robust stochastic programming method

2 案例研究

2.1 区域概况

三江平原地区牡丹江灌区位于黑龙江省东南部(131°13′～133°37′E，44°57′～46°12′N)，耕地面积为3.07×109m2，所辖12个现代化农场。灌区内土壤肥沃，水资源丰富，主要农作物为水稻、大豆、玉米，以井灌为主。然而，近些年随着作物种植面积的不断增加，作物需水量增大，导致灌区用水量压力增大，水资源危机加重。实际配置水资源量如果小于农作物的需水量,供水不足将造成农作物减产，增大惩罚成本，若满足农作物需水量，则又增加用水成本和系统供水风险。因此，本文运用ITRM有效的平衡系统成本和风险，解决灌区水资源分配问题。

2.2 参数确定

选取水稻、大豆、玉米3种作物为研究对象，根据《牡丹江统计年鉴》[24]、《黑龙江垦区统计年鉴》[25]等相关资料可以得到3种作物的灌区种植面积、单位面积灌溉用水区间值，作物灌溉面积比例参照文献[27]，水稻、大豆、玉米分别为100%、10%、10%，根据文献[24-25]和当地多年统计数据，得到作物单位面积最小灌溉量和最大灌溉量(表1)。以灌区2011年3种作物种植面积数据为已知条件，将作物单位面积最小(最大)用水量乘以作物种植面积、作物灌溉面积比例，得到作物最小(最大)需水量，查阅文献[24-25]得到灌区水量分配的相关经济系数(表2)。根据《黑龙江省农垦水利志》[26](1987—2015年)对灌区多年天然降水量的统计结果，可知1992、2002、2008、2011年灌区的降水量为400～450 mm，1987、1990、2009、2013年降水量为600 mm以上，其他年份降水量在450～600 mm之间。把来水量水平分为高、中、低3个水平，由统计结果可知，中流量年份比高降流量和低流量年份多，且高流量和低流量出现概率相近，故假设预测年份的降水量水平高、中、低出现的概率为0.2、0.6、0.2。查阅文献[27]获得地下水和地表水的供水比例为4∶1。其中地下水的主要补给来源为侧向径流补给[28]，2011年全年牡丹江地区地表水过境水量为2.482×1010m3，但其提水量2.3×107m3，仅占过境水量的0.093%。根据《牡丹江统计年鉴》[24]、《黑龙江垦区统计年鉴》[25]以及多年数据统计分析，得到灌区在不同来水量水平下的可供水量区间值(表3)，灌区地表水最大可供水量为6.2×108m3，最小蓄水量为1.1×108m3，地下水最大可供水量为9.7×108m3，最小储蓄量为2.55×108m3。

表1 灌区作物种植面积及单位面积灌溉用水量Tab.1 Irrigation crops area and water per unit in irrigation district

表2 灌区作物最大最小需水量、预先配水量和经济系数Tab.2 Irrigation corps maximum and minimum water distribution, target value of crops water distribution in advance and economic parameters

表3 不同来水量水平下农作物灌溉水源可用水量Tab.3 Water available for crops irrigation under different water inflow levels

2.3 模型计算结果与分析

图2为灌区用于水稻、玉米、大豆的最优目标配水量，其中地表水最优目标配水量为6.39×107m3，地下水为2.696 8×108m3，在中水平流量下灌区可用的地表水、地下水资源量依次为[2.25×108,2.42×108] m3、[3.25×108，3.47×108] m3，此时配水量充足，不存在缺水。而在低流量情况下，灌区的地下水可用水量为[2.58×108,2.76×108] m3，此时可分配水量几乎达到上限，作物供水存在缺失。可能的原因是:①水资源不合理开发，过度利用地下水。②缺少合理的规划和利用。

最优目标配水量由模型第1阶段得到，最优分配水量则由式(19)确定。鲁棒优化方法旨在第2阶段中对成本期望进行追索，并对系统的风险进行评估。表4中给出了ρ取不同值时，对应的缺水量和最优配水量。当ρ=0时，模型为普通区间两阶段随机规划模型，代表了决策者对风险持中立态度，不考虑成本可变性。由表4可知：①对于水稻，地表水的决策变量为0，当ρ=0时，在低、中、高3种来水水平下，其缺水量分别为[3.68×106，5.68×106] m3、[1.53×106，3.53×106] m3、[2.10×105，1.21×106] m3，因此，最优配水量为[4.419×107，4.619×107] m3、[4.634×107，4.834×107] m3、[4.866×107，4.966×107] m3。由表3可知，水稻的地表水最小需水量为[4.321×107，4.444×107] m3,可满足水稻的供水需求。对于玉米，地表水的决策变量为1，当ρ=0时不产生缺水量，最优配水量为6.03×106m3。在供水量充足的情况下，系统更偏好避免惩罚风险，所以将目标配水量上限作为最优目标配水量。②随着ρ的增大，缺水量不断增加。例如，在低水平流量下，当ρ=0.4，1，2时，水稻的地下水缺水量为[2.179×107，2.788×107] m3、[3.305×107，3.877×107] m3、[3.628×107，4.356×107] m3，最优配水量为[1.716 1×108，1.767 0×108] m3、[1.607 2×108，1.664 4×108] m3、[1.559 3×108，1.632 1×108] m3，玉米的地表水缺水量为0 m3、[8.3×105，9.7×105] m3、[1.02×106，1.34×106] m3，最优配水量为6.03×106m3、[5.06×106，5.20×106] m3、[4.69×106，5.01×106] m3。低水平时系统来水量较少，通过减少配水量来调节系统的最优配水量，即，鲁棒系数越大，系统的稳定性越强。模型增加了作物缺水量，降低了作物的配水量，从而使系统的稳定性增加。③当ρ逐渐增大时，作物的缺水量随之增大，但当ρ≥3之后，缺水量几乎不再变化。例如，当ρ=2,3,5时，在中水平流量下，大豆的地表水缺水量为[8.80×105，1.19×106] m3、[1.32×106，2.58×106] m3、[1.36×106，2.60×106] m3，最优配水量为[6.81×106，7.12×106] m3、[5.42×106，6.68×106] m3、[5.46×106，6.64×106] m3，玉米的地下水缺水量为[6.23×106，6.88×106] m3、[7.22×106，8.67×106] m3、[7.22×106，8.67×106] m3，最优配水量为[1.723×107，1.788×107] m3、[1.544×107，1.689×107] m3、[1.544×107，1.689×107] m3，缺水量的增加会使系统稳定性增加，但为了保证作物正常生长的最小需水量，缺水量不再增大，此时系统趋于稳定。

表4 不同ρ取值的作物缺水量和最优配置水量Tab.4 Crops water shortage and water optimal allocation of different values of ρ

续表4

表5 决策变量值Tab.5 Value of decision variable

图2 作物最优目标配水量Fig.2 Optimized allocation targets for different crops

最优系统成本区间如图3、4所示，系统成本随着鲁棒系数的变化而变化，呈递增趋势。如图3所示，当ρ=0时，最优系统总成本为[1.104 32×109,2.049 95×109]元，当ρ=1时，模型最优系统总成本为[1.331 55×109，2.235 76×109]元。当ρ=5时，最优系统总成本为[1.943 77×109，2.657 69×109]

元。在低流量水平下(图4a)，最优系统成本在[6.835 5×108，9.286 7×108]元(ρ=5)和[3.693 9×108，6.962 5×108]元(ρ=0)之间变化。在中流量水平下(图4b)，最优系统成本在[6.496 7×108，9.130 5×108]元(ρ=5)和[3.683 3×108，6.864 5×108]元(ρ=0)之间变化。在高流量水平下(图4c)，系统成本在[6.105 5×108，8.160 2×108]元(ρ=5)和[3.666 1×108，6.672 5×108]元(ρ=0)之间变化。对比图3、4，随着水资源最优分配量的变化，系统成本呈现一定的变化规律：①鲁棒系数增加，引起系统成本增大，当ρ≥3之后，成本几乎不变，说明系统已经趋于稳定。②随着鲁棒系数增加，成本的上下限差值变小，系统的稳定性增加，经济性和稳定性得到了较好的平衡。③较高的成本对应较高的缺水水平。当可用水量较高时，决策者可利用的水资源量也会较多，如果实际分配量较少，则会产生较高的系统风险和较多的惩罚成本；相反，如果可用水量较少，则决策者需要减少实际供水量，采取保守决策，降低系统风险增加稳定性。决策者可以根据系统分析结果，针对灌区实际情况，制定风险和经济相协调的水资源配置策略。

图3 最优系统总成本Fig.3 Optimized net system cost

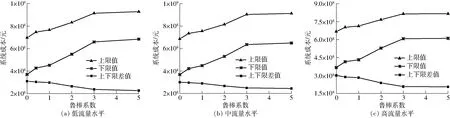
图4 不同流量水平下最优系统成本Fig.4 Optimized net system cost under different water inflow levels

3 结论

(1)针对水资源分配过程中存在风险的问题，将鲁棒优化方法与两阶段规划方法耦合，建立了区间两阶段鲁棒优化模型，以三江平原牡丹江灌区农业水资源配置为例进行了研究。模型结果表明，系统总成本随着鲁棒系数的变化有一定的规律。当模型不考虑系统风险时，即ρ=0时，系统成本在[1.104 32×109,2.049 95×109]元之间变化，随着鲁棒系数的增大，模型的缺水量增加，使得系统的稳定性增强、成本增加，当ρ=0.4、1、2时，系统成本分别在[1.263 25×109，2.185 67×109]元、[1.331 55×109,2.235 76×109]元、[1.608 79×109,2.415 52×109]元之间变化，但当ρ=3、5时，系统缺水量不再增大，此时系统达到稳定状态，成本在[1.903 27×109,2.634 75×109]元、[1.943 77×109,2.657 69×109]元之间变化。由此可知，在不同来水量水平下，通过增加鲁棒系数增加模型结果的可行性，对灌区的用水成本、系统的稳定性和系统的风险三者之间进行了充分的权衡，使配置方案更具有实际操作性和灵活性。

(2)与传统区间两阶段随机规划模型相比，区间两阶段鲁棒优化方法不但可以有效地解决不确定条件下的随机问题和区间问题，鲁棒优化方法的加入可以捕获规划过程中产生的风险问题，避免优化结果出现高风险状态，弥补了模型存在风险的缺陷，增强了系统的稳定性。将区间两阶段鲁棒优化方法应用到灌区水资源优化配置中，验证了模型的应用性和有效性。模型结果表明，通过鲁棒系数的变化，生成一系列对应的不同风险水平、不同情境的可行性方案，显示了系统经济性和系统稳定性之间的权衡。