融合RBF的二值神经网络推荐模型

雷 妍 贾连印 李孟娟 左喻灏 游进国 李晓武

1(昆明理工大学信息工程与自动化学院 云南 昆明 650500)2(云南省计算机技术应用重点实验室 云南 昆明 650500)3(云南师范大学图书馆 云南 昆明 650500)

0 引 言

迅猛发展的互联网资源让用户可以随意获取海量的媒体、文档信息以及服务等，与此同时，资源的快速增长也必将导致资源过载的问题，使得人们面临“信息丰富、但有用信息获取困难”的窘境。为有效解决这一问题，协同过滤等多种信息推荐方法被提出并已被广泛应用在新闻、社交、音乐、电影以及电子商务等多个领域。

为使推荐系统更加智能化，快速并准确地找到推荐对象，目前众多学者纷纷将神经网络引入到推荐领域中，神经网络具有快速性、自适应性以及鲁棒性等特点[1]，如今已被广泛应用到推荐系统中。然而传统的神经网络为全连接网络，存在计算成本和存储开销高等不足，从而难以扩展为深层网络。为解决这些问题，Lecun等提出的卷积神经网络(CNN)[2]引入局部连接(每个神经元只和上一层的部分神经元连接)、权值共享(一组连接共享一个权重)、下采样等技术，大幅提高网络的训练效率，同时使得神经网络扩展为深层网络成为可能。为进一步提高CNN网络中最核心的卷积操作的效率，近年来提出二值化网络[3]将权值二值化或权值和输入均二值化，并通过二值化将卷积中的乘法操作转化为加法或减法操作，从而进一步提高网络的训练效率。对权值或输入二值化虽会损失数据精度导致最终结果在准确率上有所降低，但研究表明，在特定数据集上，其在具有远高于实值网络训练效率的同时，依然具有和实值网络可比的准确率[3]。

仅仅采用二值化时可能会造成推荐效果不佳，为在推荐系统提升速率的同时保证一定的准确率，可利用亲属网络将用户进行同类别的分类。RBF神经网络是一种常见的单隐层前向神经网络模型，具有快速的学习方法、简单的网络结构和较好的推广能力[4]，通常被应用在模式识别、故障诊断、数据预测和预测控制等问题中。此外，RBF网络可以以任意精度逼近任意连续函数，因此也十分适用于解决推荐中的分类问题。

基于此，本文将二值化、RBF网络、CNN网络结合起来，通过二值化加快网络训练速度，通过RBF网络筛选出具有相似特性的用户群，建立用户可信任的亲属网络，最终将用户所建立的亲属关系矩阵导入CNN中实现推荐。在多个数据集上的扩展实验结果表明，本文提出的方法相比传统的推荐方法在准确度和效率上都得到了较为明显的提升。

1 相关介绍

在目前针对推荐系统的研究当中，常见的推荐算法有：基于协同过滤[5]、基于Bayesian技术[6]、基于聚类[7]和基于关联规则技术[8]的推荐算法等。

目前应用最广泛的推荐算法是基于协同过滤的推荐算法，该算法根据用户与用户之间爱好的相似性建立相关联系来进行推荐。首先对与目标用户相似的用户进行行为分析，以此来推断目标用户对特定产品的喜好程度，然后根据喜好程度排序并进行相应的推荐。该算法的不足主要在于存在冷启动问题，若矩阵相对稀疏，则模型很难为目标用户找到相近用户。Bayesian技术利用决策树创建相应的模型，节点和边表示用户以及相关信息，这样训练出来的模型非常小，该技术只适用于用户兴趣爱好变化较慢的场合。聚类技术首先将具有相似兴趣爱好的用户分配到同一个聚类中，然后根据聚类中其他用户对某一特定商品的评价信息，预测目标用户对该商品的评价。这种方法依旧的不足在于：若目标用户处于某个聚类的边缘则会导致该用户的推荐精度比较低。基于关联规则的推荐算法则根据用户交易数据信息生成相应的关联规则模型，利用该模型结合用户当前的购买行为向用户产生推荐，关联规则模型的生成可以离线进行。

Hubel[9]在1959年受生物自然视觉认知机制启发提出“深度学习模型”的概念。1980年Fukushima[10]提出了CNN的最初模型——neocognitron。2003年，Behnke[11]对CNN进行了总结，CNN的主要特点是卷积运算操作，利用卷积层挖掘数据局部特征并提取全局训练特征和分类，人们利用这一特点将CNN运用到多个领域并取得了较好的成绩，如图像检测[12]、自然语言处理[13]和信息分类推荐[14]等。

卷积神经网络基本结构如图1所示，主要包括：输入层、卷积层、降采样层、全连接输出层。

图1 卷积神经网络基本结构

卷积层：输入原始信号经过卷积运算操作后特征有所增强，噪声也会相应降低。

采样层：即池化层，信号通过池化层优化后复杂繁琐的特征会有所减少，例如采用卷积核为2×2进行池化，每个元素都是1/4，将卷积运算后得到的有重叠的部分去掉了。

全链接输出层：在整个卷积神经网络中起到“分类器”的作用。

卷积神经网络一经提出后，成为炙手可热的话题，成为诸多学者研究的对象。2015年11月，来自加拿大蒙特利尔大学实验室团队的Matthie Courbariaux[3]提出二值神经网络BinaryConnect。BinaryConnect在前向传播和反向传播中对数据进行二值化1或-1，不仅在模型的存储空间上进行了压缩以此节省大量的存储容量，并且由于二值化操作在卷积运算中去掉了乘法运算，只需进行加减运算，降低接近三分之二的矩阵运算，因此大大加快了运算速度，训练时间和存储空间开销都得到了大幅度优化。

2 模型设计

本文提出的融合RBF的二值神经网络推荐模型的基本处理步骤如下：首先将初始数据进行二值化预处理；其次利用RBF网络对处理过后的矩阵数据进行分析计算，构建可信任的亲属网络，进而得到可信任的亲属用户项目矩阵；最后将亲属用户项目矩阵导入卷积神经网络中进行二次筛选分类，得到输出的推荐结果。融合RBF的二值化神经网络模型结构如图2所示。

图2 融合RBF的二值化神经网络模型

2.1 数据预处理

考虑到用户行为矩阵中实值数据精度较大，导致训练速度较慢且需更多的存储空间，从而降低模型的训练和预测性能。因此，本文基于二值化的方法对用户行为矩阵中的数据进行预处理。通过二值化将矩阵中实值数据转化成二进制的数据，通常二值化方法主要有确定性二值化和随机二值化两种[3]。

确定性二值化：按照下式将实值转化为二进制位。

(1)

式中：xb是二进制变量，x是实值变量，λ为评级特定阈值。

随机二值化：根据一个计算的概率对实值进行二值化处理：

(2)

式中：P为界定x的一个概率阈值，且:

(3)

由于式(2)的方法需要使用到硬件产生随机数[3]，在计算上(软件和硬件上)花费较多成本，而第一种方法是线性分段的，能对应连续又有界的形式，因此本文采用式(1)进行二值化处理。

2.2 利用RBF建立亲属信任网络

如图3所示，RBF网络是一种三层前向神经网络，包括输入层、隐含层和输出层。RBF网络核心思想为：用RBF作为隐单元的“基”构成隐含层空间，将输入直接映射到隐含层，隐含层将低维向量按照一定规则映射到高维，从而使得在低维空间中线性不可分的样本在高维空间中线性可分。

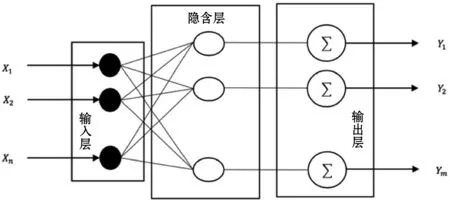
图3 RBF网络基本结构

确定RBF网络性能与结构的因素主要有三个：径向基函数(RBF)的中心矢量、方差以及隐含层到输出层神经元之间的连接权值。确定映射关系即确定RBF的中心点。输入层到隐含层的权值固定为1，隐含层到输出层的映射是线性的，所以网络的最终输出是隐单元输出的线性加权。

将二值化预处理后的用户矩阵导入RBF网络中，筛选出用户邻近特性进行分类，从而建立用户可信任的亲属网络。本文RBF网络模型的径向基函数选用最常用的高斯函数，其激活函数表示为：

(4)

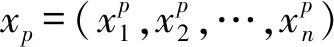
(5)

式中：h表示隐含层节点数量，wij(i=1,2,…,n)表示隐含层到输出层的权值，yj为第j个输出节点的实际输出。若d为样本矩阵的期望值，P为样本总数，则方差可表示为：

(6)

RBF网络的具体训练步骤为：

1) 确定高斯函数中心ci。

(1) 随机选取h个矩阵样本作为中心，ci表示第i个中心ci(i=1,2,…,n)。

(2) 按照最近邻规则分组将所输入的数据样本集合按xp与中心为ci的距离将xp分配到输入样本的对应最近的聚类集合∂p(p=1,2,…,n)中。

(3) 再次调整中心ci：计算聚类集合∂p中的平均值即为新的中心ci，若新的中心ci与上一次的中心ci一样，则此时的中心ci为最终结果，否则重复步骤(2)直至确定最终的RBF网络的最终高斯函数中心。

2) 确定方差σi。

由于RBF网络的基函数为高斯函数，因此可得出下式：

(7)

式中：cmax为各个中心之间的最大距离。

3) 确定权值wij。

隐含层和输出层之间的连接权值可用最小二乘法按如下公式进行计算：

(8)

2.3 卷积过程

卷积神经网络是一种前馈神经网络，由输入层、卷积层、采样层和输出层组成。其中每一层的输出作为下一层的输入。卷积层又称为特征提取层，通过滤波器提取局部特征，经过卷积核函数运算产生特征值，输出结果作为采样层的输入。采样层对卷积层产生的结果进行采样，得到局部最优特征，故也称特征映射层，本文模型中的卷积神经网络具体步骤如图4所示。

图4 卷积神经网络步骤图

首先将得到的基于用户亲属关系筛选过后的用户信息矩阵作为CNN卷积层的数据输入进行特征提取，利用q×q的滤波器对输入矩阵进行卷积操作，即：

ci=f(w·X+b)

(9)

式中:ci代表第i个特征值，函数f为卷积核函数，w为滤波器，X为局部特征矩阵，b为偏置值。因此，特征向量C为：

C=[c1,c2,…,cn]

(10)

(11)

卷积层结合采样层组成了不同类型的特征提取层，其中每种类型的特征提取层设为m个，因此全链接层的特征向量V为：

(12)

下采样层输出的特征向量作为全链接层的输入，然后利用Softmax输出分类结果，并根据训练的实际分类标签，采用反向传播算法对模型参数进行梯度更新。即：

P(y|V,Wsoftmax,bsoftmax=softmax(Wsoftmax·V+bsoftmax)

(13)

式中：Wsoftmax∈R|V|，bsoftmax为偏置项。

最后，利用训练好的融合亲属网络的二值神经网络模型，将最终得到的特征矩阵转化成向量，并用分类器进行模型训练和分类。

3 实验结果及分析

为了验证本文方法的有效性，在Windows系统下使用Matlab工具进行实验，实验中参照文献[3]将参数评级特定阈值设置为0.6，并采用了来自Kaggle平台的四个数据集：COMP、TMDB、Movie以及AISBI，所有数据集里的数据都采用5分制计数，评分越高则表示用户对某部特定的电影越喜欢。为方便评估并确保实验的可重复性，本文实验将数据集随机并多次分为训练集和测试集，抽取数据集中80%的数据作为训练集，余下20%的数据留作测试集，并取多次实验结果的平均值作为最终结果。

该实验采用准确率ACC作为推荐系统的评测指标，其计算用户的预测推荐样本与实际推荐样本的偏差，ACC的计算公式为：

(14)

式中：{p1，p2，…，pn}为n个用户预测推荐样本集合，{q1，q2，…，qm}则为参考数据集中用户的实际推荐样本集合，m代表实际推荐样本的总个数，ACC的值越高，说明推荐质量越好。

基于本文所提出的模型方法在上文提到的四个数据集上多次迭代进行实验，其对应结果如图5所示。从实验结果观察可知，在不同数据集中前期随着训练次数增加，ACC都表现出增长的趋势，而在模型训练七次或更高次数之后，准确率趋于稳定。另外，该模型在不同数据集中表现出来的推荐效果也有所不同，但基本呈现出数据集越大，模型的预测结果越好的现象。其中在数据最密集的AISBI数据集中，ACC最大。而在Movie数据集中数据较为稀疏，特征不足因此预测效果不佳，所呈现出的ACC普遍较低。

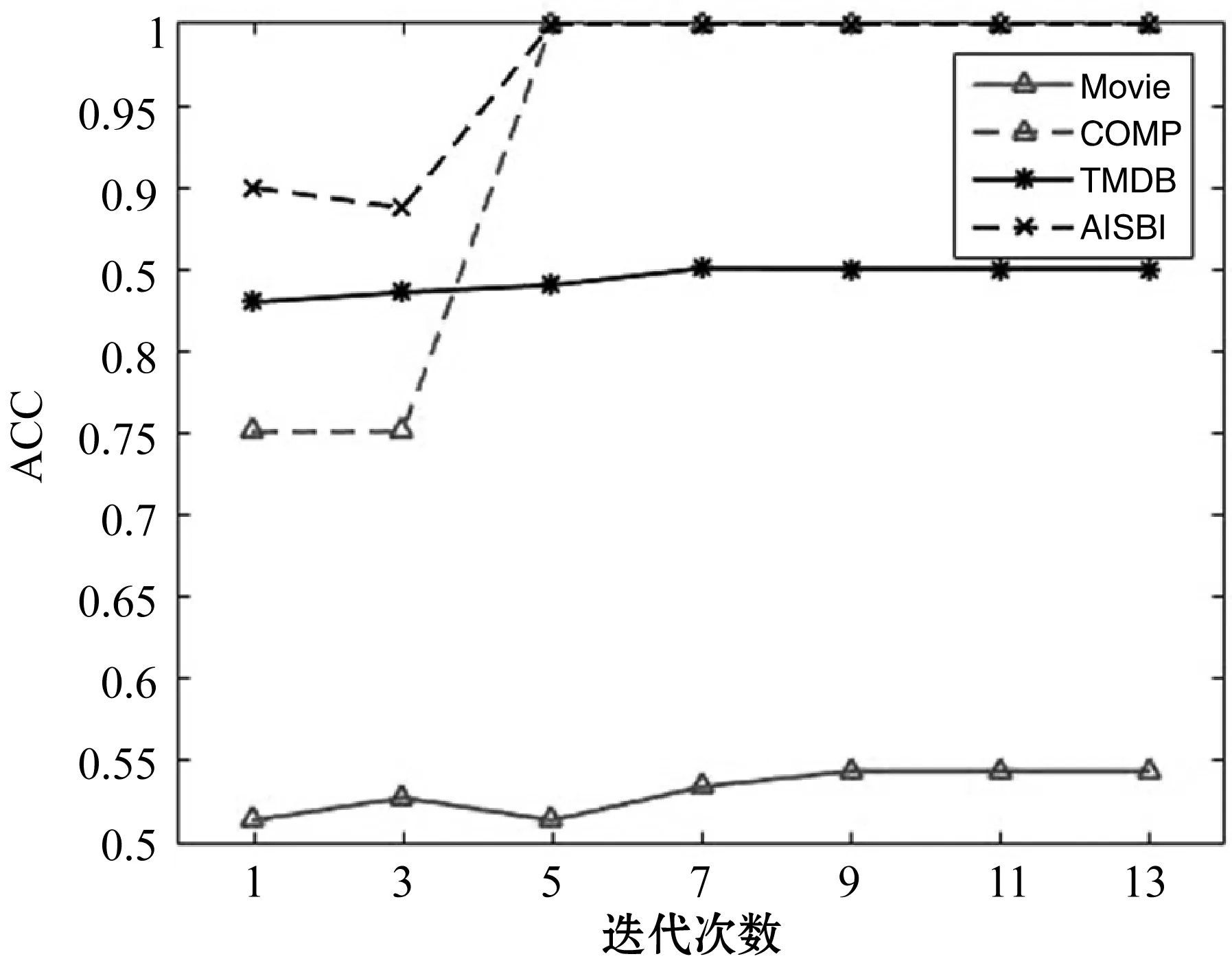
图5 不同数据集的准确率对比

为了验证本文所提出的融合RBF的二值神经网络推荐模型(RB-CNN)的推荐效果，本文将与文献[5]中基于支持向量机(SVM)的分类推荐算法、文献[6]提出的基于深度置信网络(DBN)的推荐方法以及文献[7]提出的基于逻辑回归(LR)的推荐模型训练后得出的实验结果在推荐的准确度指标上进行对比，其最终结果如图6所示。

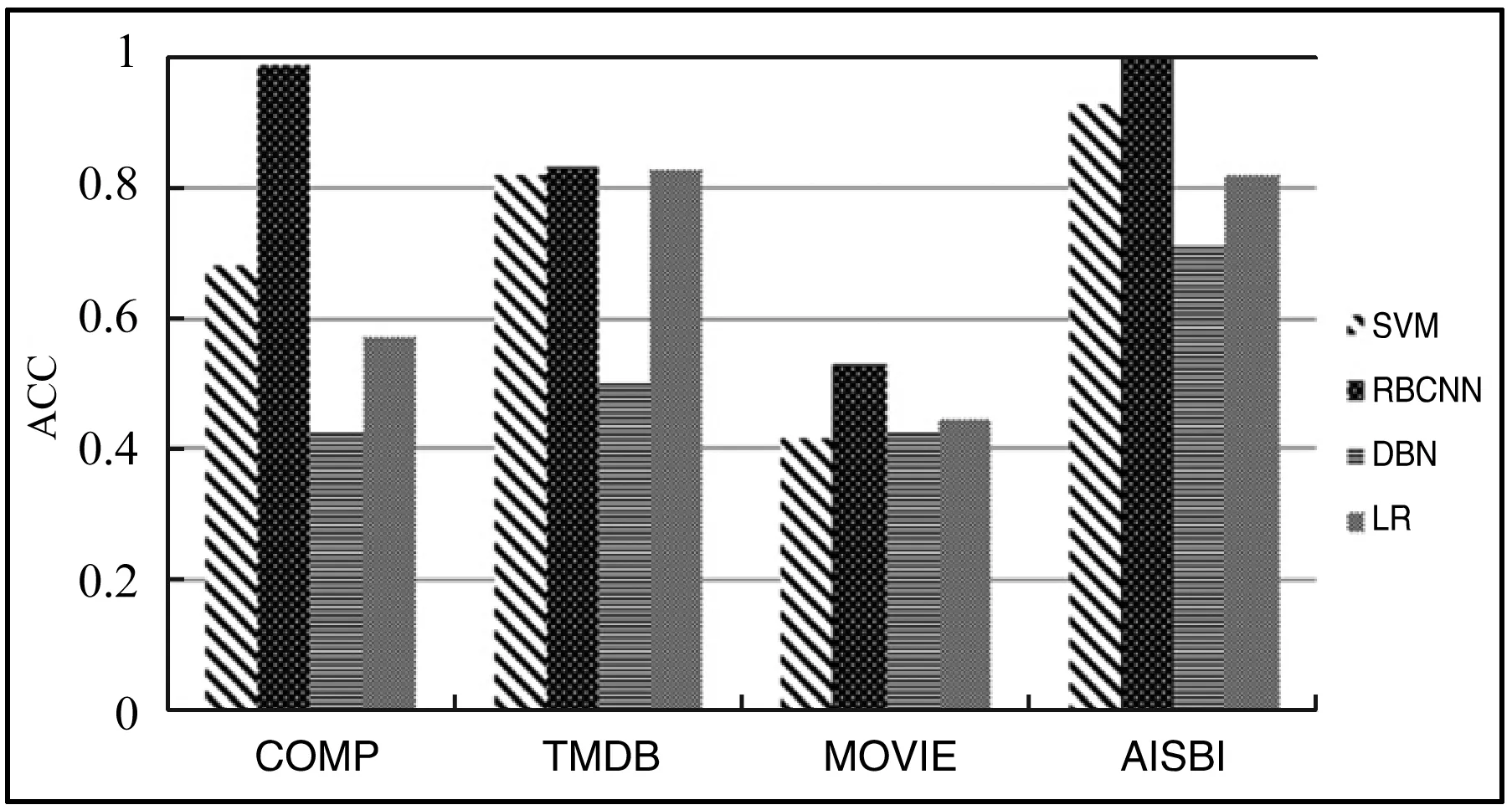
图6 不同算法在不同数据集上的准确率对比

从图6中我们可以发现，在数据量较大的数据集COMP和AISBI中本文所提出的方法明显优于其他三种算法，在数据TMDB中本文方法明显优于DBN但与其他两种方法基本持平，而在Movie数据集中由于本身数据量稀疏导致特征不足，四种算法表现出的推荐效果均不佳，但本文所提出的方法依然有一定优势。若数据矩阵的稀疏性导致特征值不足，用户属性与推荐目标的属性所发生的相互联系就会十分薄弱，因此难以达到更好的推荐效果。这也给了我们一个启发，为了达到更好的推荐效果，以后需要关注如下问题：如何更好地挖掘用户和项目属性的关联，以及如何选取合理的用户邻近点，这也是下一步工作研究的方向。

4 结 语

本文提出RB-CNN模型以实现高效的推荐，通过对推荐系统中的用户属性和项目属性建立了RBF网络，使用径向基函数计算用户与用户之间的相似度矩阵，再结合卷积神经网络进行推荐预测，扩展实验表明了本文设计的推荐模型的有效性。下一步计划针对数据矩阵稀疏的用户群体推荐进一步开展研究。