基于遗传算法优化BP神经网络的线损计算研究

刘亚丽 李英娜 李 川

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

0 引 言

电力网的线损率是电力工业中的一项综合性经济指标。随着社会的发展，对电力的需求和要求越来越大，并且随着城乡配电网改造和电力市场的逐步发展，精确的线损计算结果能够使我们合理地采取有效的降低线损措施，对于提高电力网的经济效益和响应我国节能政策具有很大的实际意义。电力网线损是指一定时间内网络各个元件上的功率损耗对时间的积分值的总和。配电网的特点：分支线多、节点多、连接元件多、负荷点多、结构分布复杂、自动化程度普遍较低、线损数据不易收集等，线损值又和网络电压、电流、电量、负荷率、功率因素、补偿装置的容量和位置、运行时间等诸多因素有关，因此精确计算配电网理论线损十分困难[1]。

到目前为止，国内已经提出了很多近似计算理论线损的方法：均方根电流法、等值电阻法、结点等效功率法、回归分析法、平均电流法、最大电流法、潮流计算法等。但是这些理论方法一般适应于35千伏以上电压的电网的线损计算，并且计算方法的工作量太大，不适用任何配电网，计算精度比较低。

针对目前国内配电网理论线损计算研究现状，提出了利用遗传算法优化BP神经网络的配电网线损计算的方法。通过遗传算法的选择、交叉、变异操作来优化BP神经网络的参数；通过优化得到最优参数有效地提高了配电网理论线损计算的精度，计算时间减少，稳定性增强。

1 模型建立

很多领域都有神经网络的研究。人工神经网络经过学习，具备很强的适应外界环境的能力。在网络学习时，有时只给它大量的输入，而没有指定要求的输出，这时，网络就自行根据输入的特征，对它们进行分类。并且人工神经具有很强的非线性映射，也可存储大量复杂数据，经过重复训练，BP神经网络可以逼近任意非线性函数。

但是BP神经网络算法存在一些典型的局限：误差对权重值的变化不敏感，误差梯度变化很小，调整时间长，迭代次数多，收敛慢，神经网络输出层极易陷入局部最小。

根据遗传算法优化BP神经网络的权值和阈值，得到最优个体。通过最优权值和阈值来对配电网理论线损进行预测和计算，避免BP神经网络陷入局部最优，得到更加精确的线损值[3]。算法流程如图1所示。

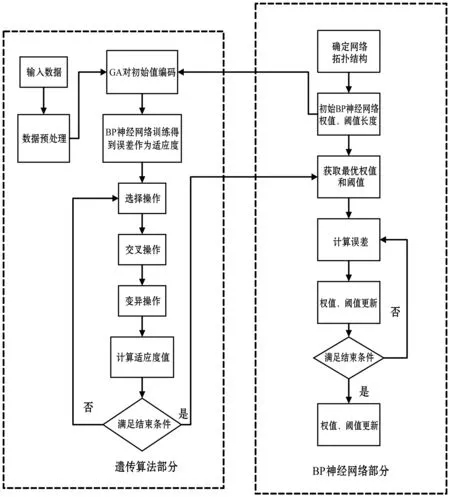
图1 GA优化BP网络算法流程

2 优化方案

GA优化BP神经网络的配电网理论线损计算，首先获取线损数据并预处理。电力网线路的特征参数有配电线路的有功电量、无功供电量、配电变压器的容量、配电线路长度、配电变压器的台数、配电线路总截断数。由电力网的特征参数得到训练集、预测集并对得到的训练集、预测集分别进行归一化处理，构建线损的神经网络模型进行预测[4]。

导入待计算线损的电力网线路特征参数，然后将线损数据分成训练数据与预测数据。

对种群初始化采用遗传算法进行优化。先后采用选择、交叉、变异遗传操作在前代基础上产生新一代种群，计算适应度值。根据最优个体创建BP模型，采用训练数据作为BP模型的输入输出数据，进一步训练BP神经网络直至收敛。把遗传算法得到的最优个体赋给BP神经网络，用该网络拟合非线性函数，反复训练BP神经网络直至精度达到要求为止，然后建立BP神经网络拓扑结构。

模型选用3层BP网络模型，一个输入层，一个隐含层，一个输出层。由电力配电网线路特征参数作为输入层节点：有功供电量、无功供电量、配电变压器的容量、配电线路长度、配电变压器的台数、配电线路总截断数；隐含层节点数为5，网络最优，网络的拓扑结构为6-5-1；线损值作为输出，采用文献[1]的算法进行计算。

2.1 归一化

配电网线路将结构相似、运行状况相似的配电线路进行分类后，然后在每种类型的线路中任选一条线路获取特征参数，将训练集和预测集归一化处理，采用最大最小法：

y=2(xk-xmin)/(xmax-xmin)-1

(1)

式中：xk为初始值；xmin、xmax分别为初始值的最小值、最大值；y为归一化数据，从而将样本数据归一化到[-1,1]，在MATLAB中mapminmax进行归一化处理。

2.2 参数编码

一般遗传算法采用二进制算法会导致编码串过长，影响网络学习的精度和效率。本文采用实数编码，便于更大范围地精确搜索，种群的组成：隐含层数、各隐含层节点数、连接权值、阈值。其长度为：

L=(m+n+l)×Smax+n+2

(2)

2.3 适应函数

适应度表示个体优劣程度，预测线损与实际线损的均方误差为个体体适应度值，计算如下：

(3)

式中：n是输出节点个数；yi是i个节点期望输出结果；oi为i个节点的预测输出结果；k为适应函数系数。

2.4 遗传算法

通过遗传算法进化：先后用选择、交叉、变异遗传操作在前代种群的基础上产生新一代种群。具体步骤如下：

(1) 选择操作。GA算法选择使用轮盘赌方法进行选择染色体，每个个体i的选择概率如下所示：

fi=k/Fi

(4)

(5)

式中：fi为轮盘赌算法的选择的概率；Fi为个体i的适应值；k是算法系数；Pi是个体i的选择概率；n为种群个体数。

(2) 交叉操作。实数交叉法如下：

(6)

式中：akj是第k个染色体在j位交叉后的染色体；alj是第l个染色体在j位交叉后的染色体；b是[0,1]间的随机数。

(3) 变异操作。选取第i个个体的第j个基因aij进行变异，变异操作如下：

(7)

式中：amax为基因aij的上界；amin为基因aij的下界;f(g)=r2(1-g/Gmax)中r2为随机数；g为迭代数；Gmax为最大进化次数；r为[0,1]随机值。

3 算法实例

基于MATLAB对配电网线路进行BP神经网络的模型构建，进行线损计算的仿真。通过某地区的68条线路进行线损计算。采用其中的60条线路数据作为样本，进行训练GA优化后的BP神经网络，剩余线路数据作为测试样本，最后进行线损仿真计算。设自变量为x1、x2、x3、x4和因变量y。其中：x1为月有功功率供电量；x2为月无功功率供电量；x3为配电变压器总容量；x4为线路总长度；y为线损值[3]。通过归一化后的数据，得到BP神经网络的标准输入和输出量。经过多次实验计算，遗传算法中的参数有变异概率m、种群大小n和交换概率c。遗传算法三种参数最优取值是：m=0.096，n=60，c=0.91[9-10]。根据隐含层BP神经网络训练精度来确定隐含层节点数，不断调整隐含层节点数p，直到达到精度值。

经过分析与调试确定BP神经网络模型隐含层节点数为5个，模型为6-5-1。根据文献[2]中的68组数据，进行配电网线损仿真。仿真结果如表1所示，其中：EE为线损误差平方和；EC为线损相对误差百分数；E为误差;N为训练次数;T为训练时间；A表示EC<0.05%;B表示0.05%≤EC<1%；C表示1%≤EC<5%；D表示5%≤EC<10%；E表示EC≥10%。

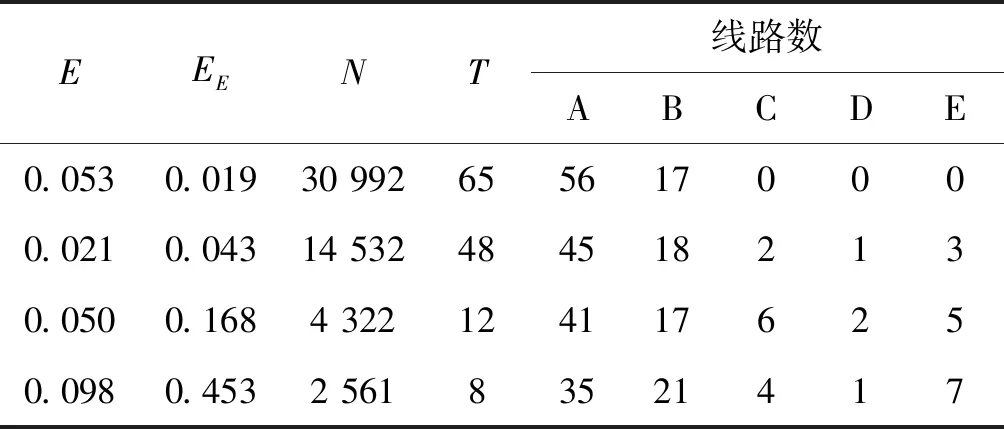
表1 仿真结果

通过文献[5-7，9]中的实例,进行实验结果比较。表2为种群遗传算法优化后的BP神经网络误差。其中：H为隐含层节点数；S为学习速率；M为动量因子；ES为误差平方和。

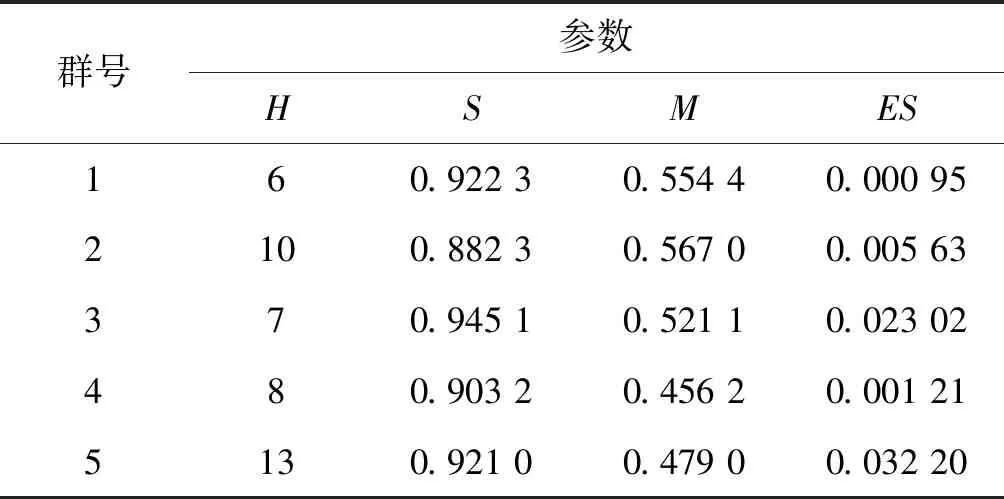
表2 误差

表3为4种算法的误差比较，其中F表示EC<1%。根据表1和表3结果分析比较，遗传算法优化BP神经网络的训练次数小于BP算法、RBF算法[8]。

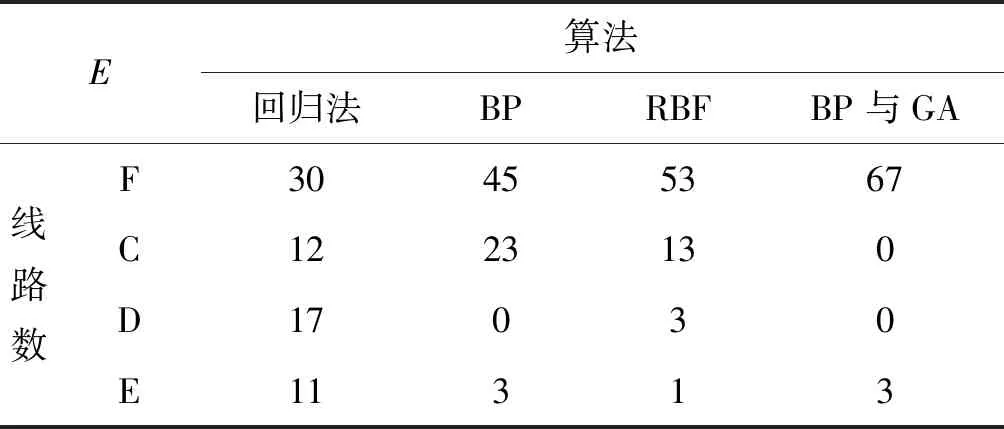
表3 4种算法的误差比较

将表2中的实验结果中的ES求和得0.063 01。如果采用分群算法将种群分群，回归算法得到偏平方和为1.027 78[11]。盲目选BP神经网络模型参数，遗传算法优化BP模型训练样本后的平方误差和为0.198 22。因此遗传算法优化BP神经网络算法计算更精确。

4 结 语

本文通过将遗传算法和BP神经网络结合起来来计算线损。利用遗传算法来计算出BP神经网络的最优权值和阈值，根据BP神经网络空间拟合性映射配电线路参数与配电网线损之间的非线性关系。最终确定BP神经网络的结构参数，建立线损计算的模型，能够比较精确地进行线损理论计算。