基于贝叶斯推断的复杂系统可靠性分析

苏续军 吕学志

1(陆军工程大学石家庄校区 河北 石家庄 050003)2(陆军第九综合训练基地教研部 河北 宣化 075100)

0 引 言

军队通常储备大量武器、弹药和备件，如何评估和分析这种复杂系统可靠性不仅关乎这些武器系统的管理和维护，还会对训练和作战使用产生影响。利用传统方法评估和分析复杂系统可靠性的最大问题在于数据样本少。一是装备本身较少，与其类似装备较少，特别是处于研制阶段的装备，这使得装备试验数据样本少。二是有些装备可靠性高、寿命长，短时间很难产生大量的可靠性数据样本。三是对于昂贵的一次性使用的弹药类武器装备，不可能进行大量试验，因此不能得到大量数据样本。但是，还有其他来源的系统可靠性信息。例如，组件、子系统如何相互连接以在系统中发挥功能的信息；组件和子系统的测试信息可能是可用的；与组件、子系统、系统相关的工程知识，例如目视检查和其他无损检测数据。通常，从这些其他信息来源获得的数据可能会大大超过全系统测试的数据，因此将这些信息纳入分析方法可以大大提高预测和估计的精度。问题在于如何给出一种通过融合各级数据和专家知识来分析评估复杂系统可靠性的方法。

本文将使用贝叶斯方法来解决这个问题。贝叶斯方法较传统的频率方法有以下优势：(1) 适合数据稀少的情况。当数据稀少时，频率估计量(如极大似然估计)可能变得不合理；(2) 通过蒙特卡洛抽样可以很好地解决区间估计，而对于频率方法传播频率区间估计(如置信区间)会比较困难；(3) 具有通用性。而频率方法有时存在一题一法的问题；(4) 具有融合多种信息的能力，而频率方法无法在计算过程中处理“非数据”信息。

国外对贝叶斯方法在可靠性方面的应用研究比较深入。Martz等出版的《贝叶斯可靠性分析》是最早的从贝叶斯角度研究可靠性的专著[1]。随着数值模拟技术的进步，贝叶斯方法在科学研究与工程实践中都获得了更加广泛的应用。Hamada等出版的《贝叶斯可靠性》主要介绍贝叶斯方法在可靠性数据分析中的应用，重点介绍如何利用数值模拟技术有效地实现基于贝叶斯理论的可靠性分析[2]。Kelly等在著作中详细探讨了贝叶斯推断在概率风险评估中的运用[3]。文献[4-5]运用贝叶斯方法对串联系统和串/并联系统可靠性进行了研究，用β分布描述组件的先验分布，并通过复杂的β分布近似推导得到系统后验分布，但是该方法无法通过整个系统的数据来估计单个组件的可靠性。文献[6-7]提供了通过系统结构传播组件后验获得精确或近似的系统可靠性分布的方法。文献[8]提出了基于最大熵原理的评估系统可靠性后验分布矩的方法。文献[9]运用蒙特卡罗模拟方法对上述问题进行了求解，不需要进行近似推导。结果显示，通过融合系统测试数据，系统可靠性要比仅融合组件和子系统测试数据的可靠性低，对某些组件的可靠性估计值大大降低。文献[10-13]利用贝叶斯方法对复杂系统的故障数据融合问题进行了探讨。国内学者多运用贝叶斯方法研究了多种产品的可靠性，但仅关注于单层组件(系统)的信息融合。文献[14]应用贝叶斯方法分析了故障数据小样本条件下的数控机床可靠性。文献[15]应用贝叶斯方法分析了光纤陀螺光源可靠性。文献[16]应用贝叶斯方法评估了铣头可靠性。

本文将给出一种基于贝叶斯推断的复杂系统可靠性分析方法，可以集成融合各种来源的信息(全系统测试、组件测试和专家工程判断)，在系统测试数据有限的情况下或没有系统测试数据的情况下，可以一致性地预测复杂系统及其组件的可靠性。

1 贝叶斯推断概述

贝叶斯定理提供了在概率环境下，融合信息和数据以更新先验知识的数学手段。通过下面的表达式，该定理修正了先验概率，得到后验概率：

(1)

式中：Pr(H|D)为后验分布，以与假设H相关的数据D为条件；Pr(H)为先验分布，来源于假设H，与数据D独立；Pr(D|H)为似然函数或随机模型，刻画产生数据D的过程与机理；Pr(D)为边缘分布，起归一化常数的作用。

在贝叶斯推断中，用概率分布刻画模型参数取值的知识，并利用先验分布、可靠性模型和观察数据，通过贝叶斯定理给出参数(或多个参数)的后验分布，连续形式通常可写为:

(2)

式中:π1(θ|x)是参数θ(可能为向量)的后验分布。这个后验分布θ是所有与相关的推断声明的基础，也是模型验证方法的基础。观察数据通过似然函数f(x|θ)进入贝叶斯定理。π0(θ)是参数θ的先验分布。

分母部分f(x)是θ所有可能取值的积分，是一个加权平均分布，权函数是先验分布π0(θ)。当X为离散随机变量(如某段时间内发生的事件数)时，f(x)是恰好发生x个事件的概率，与θ的取值无关。当X为连续随机变量时，例如维修时间，f(x)是密度函数，给出了无穷小区间内x观察值得无条件概率。

似然函数f(x|θ)还有另外一个名字，即描述观察到的物理过程的随机模型。似然函数与数据收集和计算过程有着内在的联系，特定的似然函数意味着特定形式的数据。似然函数常常是二项分布、泊松分布或指数分布，对应的数据形式分别是在收到一定数量请求中成功(故障)的次数、一定时间段内的成功(故障)数量和成功(故障)时间。

π0(θ)是参数θ的先验分布，代表与数据无关的参数θ的已知信息。广义上，先验分布可以区分为有信息和无信息。正如名字所示，有信息先验包含θ可能取值的真实信息。而无信息先验使数据在后验分布中占支配地位，因此它包含的参数真实信息非常少。

进行贝叶斯推断的一般流程包括：

(1) 指定随机模型(如部件收到请求后未能改变工作状态而发生故障)；

(2) 指定模型参数的先验分布，量化认知不确定性，即对参数可能取值的认识；

(3) 观察故障过程的数据或与之相关的数据；

(4) 更新参数的先验分布以得到后验分布；

(5) 检验随机模型、数据和先验分布的正确性。

2 复杂系统及其可靠性建模

对于贝叶斯推断方法而言，系统复杂性来源于系统的复杂结构、多样化的数据来源、不同组件的可靠性随机模型、不同组件可靠性参数的先验分布。这部分主要对复杂系统的结构模型、数据类型、似然函数和先验分布进行介绍。

2.1 结构模型

现实世界中，复杂系统的组件规模是非常庞大的，组件之间的关系也是非常复杂的。为了更加清晰地论述可靠性分析方法，需要简化复杂系统的一些细节，同时保留对贝叶斯推断构成挑战的所有系统特征。

系统的一些关键特征包括：首先，从逻辑上系统可以分解成子系统，这些子系统是集中于特定任务的自然分组。一些子系统直接组合以形成系统，而另一些子系统可以嵌套在其他子系统内。系统的描述形式在很大程度上取决于什么数据来源可用，以及工程师对系统功能的了解程度。其次，有些组件和子系统的数据可用，但是并不是所有组件和子系统的数据可用。最后，复杂系统可能有若干类型。例如，一种导弹可能会有若干种型号，这主要是因为某些组件存在差异(由不同制造厂家生产，具有不同功能，当然其可靠性会不同)。认为每种类型具有不同的可靠性，可以提高估计过程的精度，并且有助于深入了解哪些种类更有可能失效。

复杂系统结构有多种图形化的描述方法，例如故障树、贝叶斯网络、可靠性框图和事件树，本文将使用事件树来描述复杂系统[17-18]。本文考虑的复杂系统有3个主要子系统，共有13个组件。图1描述了该复杂系统的事件树图。

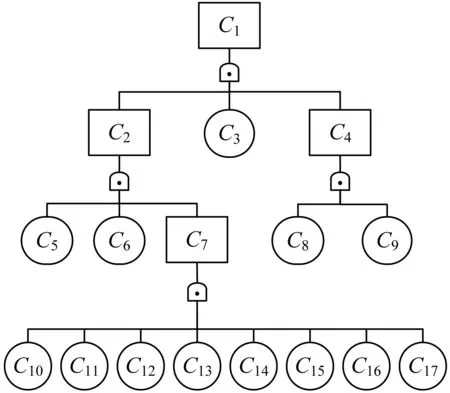
图1 复杂系统的事件树图

组件和子系统由AND门连接，这意味着为了使整个系统运行工作，需要所有组件和子系统都运行工作。该系统被标记为C1，由C2、C3、C4组成；C2由C5、C6、C7(由C10到C17组成)组成，C4由C8、C9组成。如前所述，将系统的各个部分划分为组件或子系统是主观的，并且取决于可用的信息。例如，组件C3实际上由“组件”的集合组成，如果有可用数据，则可以将其表示为具有“组件”的“子系统” 。

图1所示的系统只有13个组件，子系统和系统中组件的嵌套级别为4级，因此并不是非常复杂的系统。这种方法可以应用于规模更大的问题，但为简单起见，本文只使用了这个比较简单的例子。本文提出的方法可扩展到具有更多组件和嵌套级别的系统，同时随着系统规模变大，估计和预测的计算量将大大增加。

2.2 数据分类

在估计复杂系统的可靠性时，通常在系统，子系统和组件级别上具有测试数据和工程判断。这里考虑了4类数据来源。

(1) 全系统测试数据。例如导弹的多次飞行测试结果(成功/失败)。

(2) 组件或子系统测试数据。通常的情况是，对于部分组件和子系统有测试数据，但不是全部组件和子系统都有测试数据。

(3) 关于特定组件或子系统发生故障可能性的工程判断。它代表了有关系统正常工作及其预期设计的大量主观知识，有助于限定可靠性，用先验分布来描述。

(4) 不太精确的工程判断。指出给定系统或相关系统中的一组组件具有类似的故障概率。例如，专家可以断言导弹电池的可靠性与相关导弹系统中的电池的可靠性相似，或者电动机的可靠性相似。或者，专家可以判断给定子系统的所有组件都可能导致该子系统的故障。这表明组件的可靠性被认为是相似的，但这并不意味着组件的故障机制是相同的。

2.3 似然函数

在本文模型中，假设每个组件、子系统和完整系统的状态只有两种：成功或失效。这种二元状态是可靠性分析中最简单的状态描述方式。

二元状态的限制意味着独立测试结果服从二项分布。将整个系统表示为子系统和组件的串联形式，使得系统和子系统的状态取决于组件的状态。因此，子系统和全系统的似然函数是所有组件可靠性参数的函数，为二项分布。在二项随机模型中，Xi表示Ci成功次数的二项随机变量，可取0～ni的任何整数。输出xi的概率由分布密度Binomial(ni,pi)给出：

(3)

建模的目标是使用可用数据来估计每个组件、子系统、整个系统Ci的可靠性参数pi，重点是获得整个系统C1的可靠性估计，即p1。

如前所述，从可计算性和模型一致性的角度来看，在可靠性图的不同层次上融合数据和先验信息通常被证明是有问题的。解决这个难题的方法是通过利用事件树图得到的确定性关系将终端(组件)节点概率重新描述为非终结(子系统)节点概率。例如，从图1可以看出，子系统C7正常的概率p7等于概率p10到p17的乘积，C10到C17每个组件全部正常工作。从而:

(4)

类似地，子系统C4正常的概率为p4=p8×p9。这种方法利用了系统可靠性的边际分布，为获得所有组件和子系统可靠性的联合分布提供了一个明智的解决方法。

2.4 先验分布

在许多应用中，工程判断可以在评估系统可靠性方面发挥重要作用，特别是对于各个组件的测试数据较少的大型复杂系统。工程判断需要一定的专业知识来确定组件的先验分布，并确定哪些数据与分析相关。这里主要讨论3种工程判断：

(1) 精确信息：专家通过描述组件的故障概率分布来提供关于单个组件可靠性先验知识的精确信息。

(2) 组件分组：专家将组件归为具有相似可靠性的组件组。这个假设并不要求组件在物理上是相似的，只是它们的可靠性是相似的。例如，所有高可靠性部件可能被判断为相似。可以通过层次模型描述这种类型的信息。

(3) 无信息：专家对组件可靠性没有太多先验知识，但是仍然可以通过提供组件的可靠性先验分布来描述组件可靠性信息不足的情况。

2.4.1 精确信息

可以从几位专家获得工程判断，从每位专家获得的信息质量可能会有所不同。在模型中，假设专家m给出pi服从β分布的工程判断，这里令S1表示集合(i,m)，代表专家m给出pi的工程判断可用。β分布是一类灵活的概率分布，取值介于0和1之间，适合描述可靠性[2-3]。

更具体地，假设先验分布为：

B(pi;Nσi,m+1,Nm(1-σi,m)+1)

(5)

式中：σi,m代表专家m对pi的估计，Nm表示专家m的估计精度。请注意，这不是β分布的标准形式，之所以这样选择是将分布均值作为理想参数特征之一。因为标准的β分布β(a,b)，其分布均值为a/(a+b)，令a=Nmσi,m+1和b=Nm(1-σi,m)+1。有许多方法可以整合多个专家提供的信息，例如几何平均(对数的算术平均)和对数分布的5%和9%的分位点。本文采用平均(等权重)方法来综合不同专家的信息，具体见示例中的OpenBUGS代码。

假设σi,m服从参数μi,m和νi,m已知的β分布:

(6)

每个专家精度Nm服从参数αm和βm已知的γ分布:

(7)

总之，通过β分布可以描述pi约为σi,m的工程判断。通过描述Nm的先验分布，可以更灵活地调整估计，并根据给定数据使用贝叶斯定理来得到Nm后验分布，从而能够从经验上评估专家的专业知识。如果专家意见与数据不一致，则Nm将很小，实际上减少了专家对推论的影响。此外，该工程判断使得二项分布似然函数在σi,m点具有最大值。这种做法极大降低了所有模型参数的联合分布不一致的可能性，并且还通过将工程判断视为“数据”的形式隐式地处理聚合问题。

接下来，将通过简单例子说明了N固定和随机之间的差异，如图2所示。在两种情况下，数据为成功次数x，总试验次数n=40次，似然函数服从二项分布，成功的概率p未知。p先验分布为B(Nπ/N(1-π))，π=0.5，比较了N固定(为30)的情况，以及N随机的情况，即N服从参数α=3和β=1/10的γ先验分布(E(N)=30，SD(N)=17.32)。在每副图中，实线是N固定情况下p的后验密度估计，虚线是在N随机情况下p的后验密度估计。左图为成功次数x=20的情况，这与π=0.5的先验均值完全一致。在这种情况下，数据提供的关于N的信息不是很多，因此其后验接近于其先验数据。N的后验平均值为31.96，略大于其先验平均值30，其后验标准差为17.23，与先验标准差17.32大致相同。p的后验分布均值为0.5，其后验分布SD在N固定或随机情况下基本都为0.06。因此，在数据与先验一致的情况下N可以是随机的，不会造成任何影响。然而，如果数据和先验不一致，则N固定和随机情况下会得出不同的结果，如图2的右图(x=35)。对于N=50固定的情况，在40次试验中有35次成功，所以可以推断E(p)=0.705 7和SD(p)=0.053 26。当N是随机变量时，其N后验分布的平均值为12.27，SD为8.353 11，p的先验也显得并不重要，并且得到E(p)=0.782 6和SD(p)=0.068 76；平均值更接近数据所隐含的高可靠性，而标准偏差较大，这是因为先验分布提供的信息较少。对于N固定的情况，贝叶斯分析具有误导性，因为先验的准确性被高估了，其与数据不一致。而对于N随机的情况，贝叶斯分析相应地进行处理，将先验作为有用的信息，但不如最初想到的那么准确。

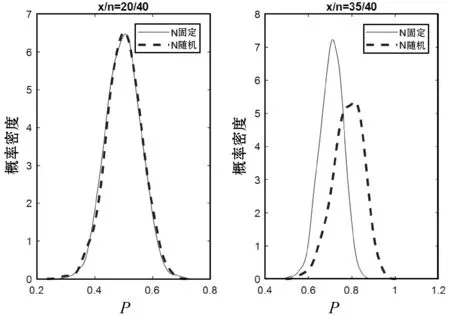
图2 比较N固定和随机两种情况下p的后验分布概率密度

2.4.2 组件分组

当关于组件可靠性的先验分布并不总是已知时，专家通常有可能将组件分配到“可靠性类似”的组。给定组中组件的可靠性不一定相同，但可交换。因此，通过假设式(5)中σi,m由ρm,g代替，其中ρm,g表示由专家m分配给组g中的组件的共同但未知的可靠性概率，这样可以对模型进行扩展。 此类信息的模型参数先验服从以下公式：

(8)

式中：S2表示i和m构成的组合(i,m)，表明专家m对部件i进行了组件分组的工程判断。

如式(8)所示，假定参数Km先验分布服从参数为ζm和ηm的γ分布，组g的成功概率参数ρm,g的先验分布服从参数δg,m和ξg,m已知的β分布。这里ρm,g可以被解释为组g内的组件pi的公共平均估计。这种方法可以利用相似的组件的知识，以增加预测能力。

2.4.3 无精确信息

对于有测试数据而无精确专家工程判断信息的组件(终端节点)，运用层次贝叶斯模型来描述组件(终端节点)的先验分布。同时，这种层次贝叶斯模型可以使系统可靠性估计对系统事件树图中包含的层次信息并不灵敏。

接下来将通过两个简单的例子来说明层次贝叶斯模型的重要性。在第一个例子中，考虑一个由3个组件串联系统(类似于C1，由C2、C3和C4组成的简单系统，没有其他组件)，并且假设在系统级别观察到4次成功和1次故障。组件先验分布没有使用层次贝叶斯模型。按照上述组件具有共同先验分布的假设，系统可靠性似然函数将与下式成正比：

(p2p3p4)4(1-p2p3p4)

(9)

其中p1=p2p3p4，组件故障独立、串联，要求所有三个组件都正常系统才正常。似然函数是根据以下事实得到的：由于4次试验成功，意味着组件C2、C3和C4全部工作，其发生概率p2p3p4。故障的概率1-P(成功)=1-p2p3p4。

如果p2到p4先验服从均匀分布，则该模型中p1的后验均值为0.507。当系统未分解为子系统，并且p1先验服从均匀分布，p1(先验也服从均匀分布)后验均值为0.714。此外，在这种不使用层次贝叶斯模型的情况下，向事件树添加组件将产生的偏差，偏差将随着系统中的组件数量的增加而变得更加严重[19]。

在第二个例子中，假设组件C2、C3和C4的可靠性不服从独立的均匀分布。相反，每个组件的成功概率服从β分布(如式(5))，参数为Jγ+1和J(1-γ)+1，其中假定参数J服从参数为τ和φ的γ分布。假设参数γ服从参数为ψ和ω的β分布：

Β(pi;Jγ,J(1-γ))

(10)

根据p2到p4的层次先验描述，以及ψ=ω=0.5，p1的后验平均值为0.718，而具有ψ=ω=1.0使得后验平均值为0.687。这两个估计在很大程度上对系统的组件数量不灵敏。这是该模型的一个重要特征，即系统不同组件和子系统数据的可用性不应在系统整体可靠性估计方面产生重要影响。

2.4.4 联合后验分布

为了获得贝叶斯推断所需的后验分布，数据中包含的似然函数信息必须与先验分布中的专家工程判断相结合。后验分布与先验分布乘以似然函数的积成正比。合成来自似然函数和先验的信息，得到模型参数联合后验分布，其与下式成比例：

[p|x,n,σ,N,ρ,K,γ,J,μ,ν,α,β,ζ,η,δ,ε,τ,φ,ψ,ω]∝

(11)

式(11)是参数p的联合后验分布的表达式，参数p在表达式的中垂直线的左侧，垂直线表示参数p依赖模型的其他参数(x,n,μ,N,ρ,K,γ,J,σ,ν,α,β,ζ,η,δ,ε,τ,φ,ψ,ω)以获得与联合后验分布成正比(∝)的表达式。S0表示终端节点/组件的集合。

在这个表达式中，假定非终端结节点概率(如元素C1、C2、C4和C7)可以根据系统事件树图描述为终端节点概率的适当函数。式(11)的第1行对应于从每个可用组件的观察数据对似然函数的贡献。第2和第3行对应于专家对组件先验分布的精确信息，而第4和第5行对应于组件分组的信息，第6和第7行对应组件(终端节点)缺少精确先验分布信息。

由先验信息产生的联合后验分布显示出明显的相似之处，但这些参数之间也有重要区别。例如，Nm的值表示专家意见的精度，而Km描述了分组内组件可靠性的相似性。

3 求解方法

3.1 马可夫链蒙特卡罗

本文中的联合后验分布非常复杂，包含多个分布，所以不能立即对复杂系统可靠性做推理和估计。

马尔科夫链蒙特卡罗MCMC(Markov Chain Monte Carlo)方法是贝叶斯计算取得的突破性进展，可以通过联合后验分布获得随机样本。MCMC可以在有限维状态空间中模拟由任何非规范化分布密度函数指定的任何的分布。一旦通过MCMC算法获得随机样本，则可以对感兴趣的任何分布特征进行推断。目前常用的MCMC有两种，一种是吉布斯(Gibbs)采样方法[20]，另一种方法是 Metropolis-Hastings算法[21]。

目前有许多种运行MCMC的软件。MCMC独立软件包括 winBUGS和openBUGS、JAGS (Just Another Gibbs Sampler，由Martin Plummer等编写和维护)、Stan(Andrew Gelman 编写和维护)； R软件的MCMC软件包包括MCMC(Charles Greyer编写和维护)、Nimble(Chris Paciorek 编写和维护)、R语言调用openBUGS、rjags、STAN的软件包。

3.2 OpenBUGS

本文将使用OpenBUGS来进行仿真计算。OpenBUGS(BUGS是Bayesian Inference Using Gibbs Sampling的缩写)是实现MCMC的免费软件，其开源版本可以从www.openbugs.info获得。OpenBUGS采用菜单驱动的脚本语言。这种脚本语言包括三部分：模型描述、数据和初值。模型描述包括似然函数、先验分布和计算量(如系统可靠度)。数据和初值可以写入脚本，也可以从独立文件读入。“#”后文字用作注释[22]。脚本示例：

Script to update rate

model { #{}间定义模型

events ～ dpois(mu) #事件数服从泊松分布

mu <- lamda*time #泊松分布的参数

lamda ～ dgamma(2.6,34) #λ的先验分布

}

Data #观察数

List(events=2,time=14)

4 示 例

接下来将运用本文提出贝叶斯推断方法对虚构的复杂系统进行可靠性分析。复杂系统的结构可以用图1的事件树图进行描述。图3对事件树图各个节点的先验分布进行了区分。有3名专家对组件给予工程判断。C10-C17有分组信息，即它们有相同的先验分布，与3名专家对应的先验分布参数ζ、η、δ、ε分别为(2, 3, 4)、(0.1, 0.2, 0.4)、(9, 10, 11)、(1, 1, 1)。C5、C6有精确的专家工程判断，C5与3名专家对应的先验分布参数α、β、μ、ν分别为(4, 3, 2)、(0.4, 0.2, 0.1)、(20, 15, 10)、(1, 1, 1)，C6与3名专家对应的先验分布参数α、β、μ、ν分别为(4, 2, 3)、(0.2, 0.1, 0.4)、(15, 10, 20)、(1, 1, 1)。

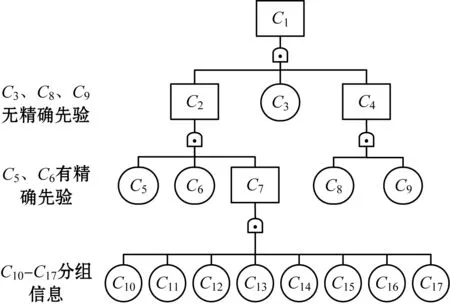
图3 先验分布类型划分

C3、C8和C9没有精确的先验分布，先验分布参数τ、φ、ψ、ω分别为1、1、2、2。各组件测试次数分别为1 276、163、182、26、183、127、20、56、110、192、193、32、195、192、98、161、29，成功次数分别为1 260、161、181、25、180、121、19、55、108、190、191、31、191、190、97、160、28。利用OpenBUGS可以实现对该复杂系统可靠性的估计和分析，OpenBUGS脚本如下：

在MCMC仿真计算中，进行了100 000次迭代(舍弃最初10 000次以达到收敛)以估计参数值。

表1给出了各组件的可靠性评估值，系统的可靠性均值、标准差、仿真误差、2.5%分位数、中位数、97.5%分位数分别为0.905 1、0.108 2、0.006 084、0.481 6、0.958 9、0.970 3。图4给出了各组件的盒图，直观地描述了各组件的可靠性范围。可见，系统可靠性偏差范围较大。图5给出了部分组件可靠性密度曲线。图6给出了部分组件的History曲线，可以看出仿真中的马尔科夫链在迭代40 000次后实现了收敛。

表1 各组件可靠性评估值

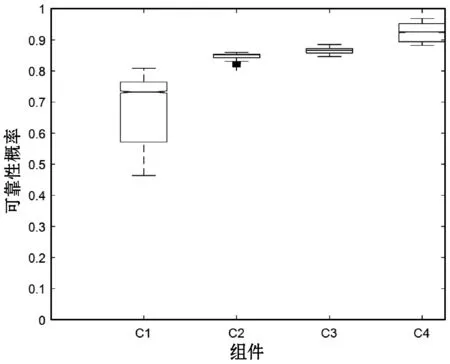
图4 复杂系统各组件盒图

(a) p1的后验分布密度(b) p2的后验分布密度

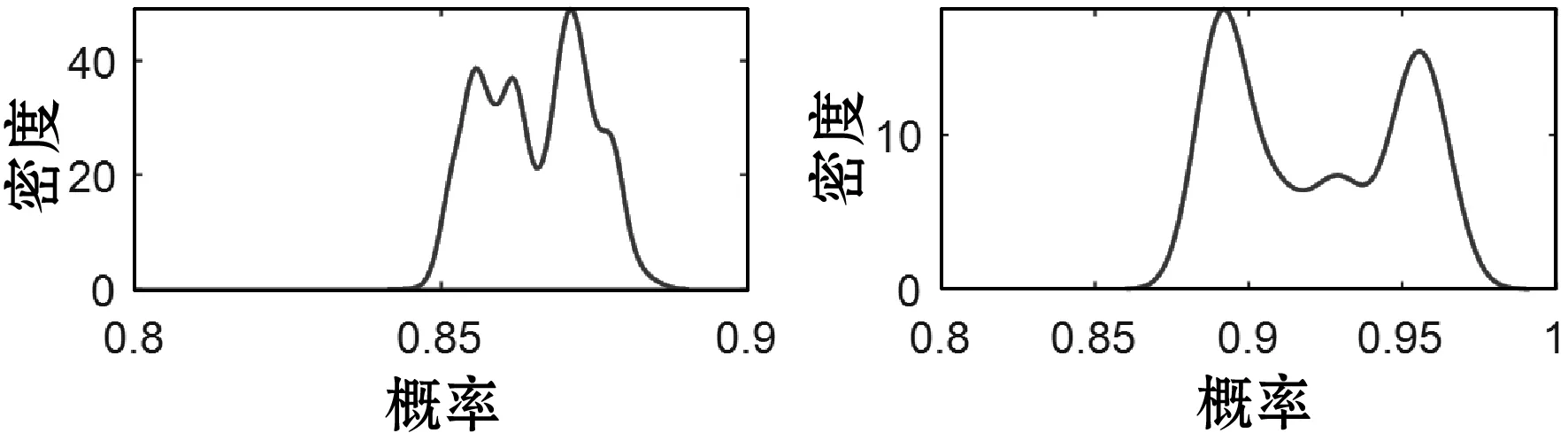
(c) p3的后验分布密度(d) p4的后验分布密度图5 复杂系统部分组件可靠性估计密度曲线

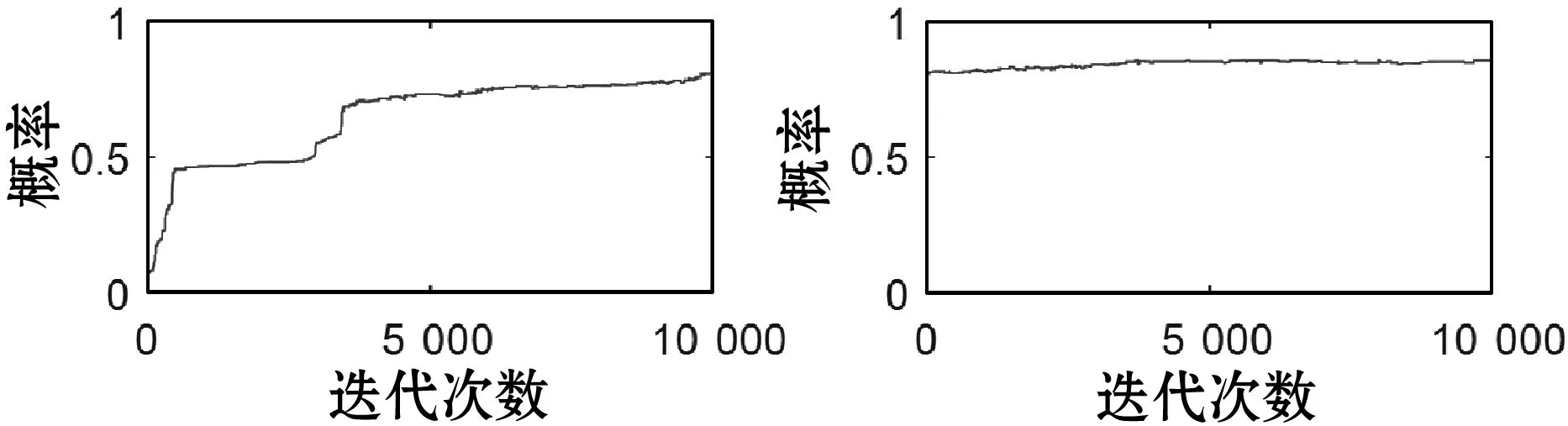
(a) p1采样曲线 (b) p2采样曲线

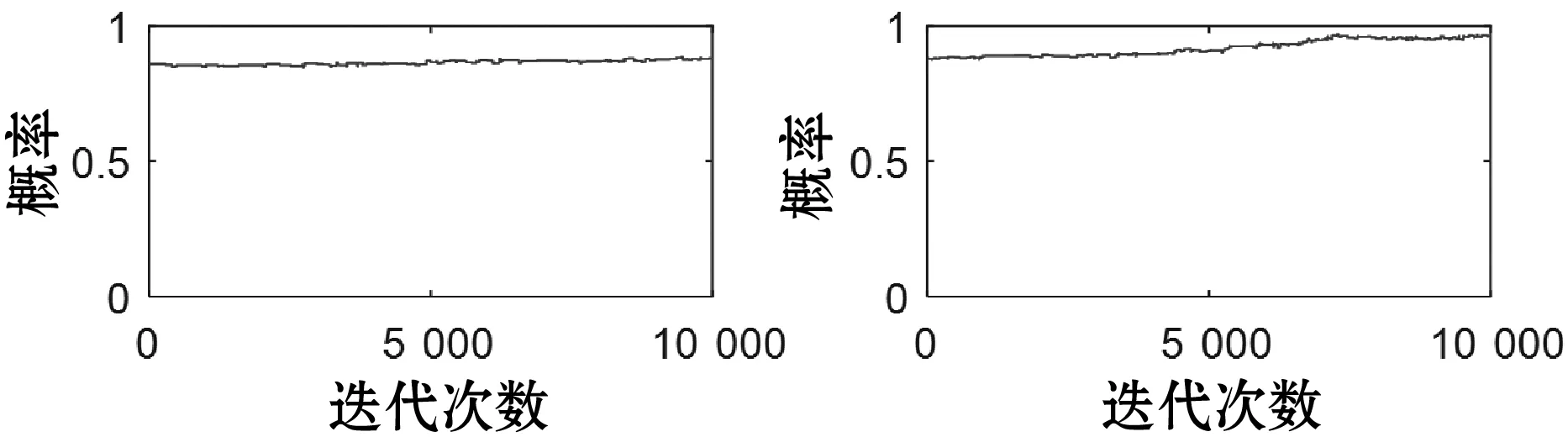
(c) p3采样曲线 (d) p4采样曲线图6 复杂系统部分组件History曲线

在实例中全系统测试数据较为充分，实验进行了1 276次，其中1 260次成功，组件的测试相对较少，介于0到200之间。根据表1，系统可靠性仿真结果为0.970 3，与实验的0.987 4(1 260/1 276)接近，也验证了贝叶斯方法在数据充分的时候与传统概率论得出的结论是一致的。通过对模型的仿真计算，验证了该方法可以有效地融合全系统测试数据、组件和子系统级测试数据和专家工程判断，可以根据可用的数据灵活选择建模粒度，一致性地估计组件、子系统、系统的可靠性参数。

5 结 语

随着武器装备系统日益复杂，成本越来越高，大量的全面系统测试逐渐变得不可行，很难得到大量的可靠性信息，可靠性的统计分析与评估面临着挑战。因此，本文提出了一种基于贝叶斯推断的复杂系统可靠性分析方法。首先，介绍了贝叶斯推断原理和一般步骤。其次，利用事件图对复杂系统结构进行建模，归纳了可用的数据类型，对组件随机模型和先验分布进行描述。再次，探讨了如何利用马尔科夫蒙特卡洛方法对模型进行求解。最后，给出了复杂系统实例，利用OpenBUGS对其进行建模和仿真计算，验证了方法的可行性与有效性。本文提出的方法可以灵活地融合组件和子系统级测试数据、专家工程判断和全系统测试数据，可以根据可用的数据灵活选择建模粒度，一致性地估计组件、子系统、系统的可靠性参数。今后，还可以将这种方法拓展到具有更复杂可靠性关系的系统、多状态系统，融合更多类型的先验知识，如物理化学等理论知识、工程试验或验收试验的结果、行业通用的可靠性数据、计算分析结果、相似产品数据等。