一种密文图像安全性评价方案

韩 啸 熊礼治 蒋鹏程 宋婷婷

(南京信息工程大学计算机与软件学院 江苏 南京 210044)

0 引 言

图像加密技术是目前为止主要的两种图像保护的方法之一，许多图像加密方案已被提出[1]。本文主要讨论的图像加密技术是根据图像的空间性、时间性、冗余度高、视觉可感知性等特性来设计加密算法[2]。但是密文图像仍存在着被破译的风险，这个时候就要减少被破解的可能性，所以需要提高算法的安全性[3]。由于图像加密算法种类越来越多，在选择使用哪种加密算法时，人们需要知道哪个算法相对其他算法的安全性更好，为此图像加密算法的安全性评价方法就被提出了。而目前对于加密算法安全性的评价，大多数都是对算法的单一指标参数进行比对，由于不同指标参数所针对的密文图像安全特性不同，单一的指标参数对于图像加密算法的安全性评价很有可能是片面的，不能全面地展示出密文图像的安全性能和适用场景。

为了能够综合比较不同加密算法的指标参数，本文提出一种基于多种指标参数横向比较的密文图像安全性评价方案，并设计和实现系统。本文先介绍采用的5种图像加密算法及其加解密步骤。然后介绍所采用算法的指标参数，如像素数量改变率、密钥空间大小、信息熵、相邻像素相关系数等,并对各个指标参数的可靠性进行分析比较。接着介绍通过MATLAB来实现本系统，并对文件照片和卫星地图照片这两类常用的“类图像”进行具体安全性分析。最后对全文进行总结。

1 图像加密算法

1.1 仿射变换加密

仿射变换是一种几何中常见的变换，该变换的公式如下：

(1)

在这里，本文选取的密钥为：

a=9.484 911 376×102，b=1.332 291 989×104，

c=5.781 391 478×103，d=8.120 794 541×104，

e=1.615 675 500×102 ，f=2.275 588 209×103。

1.2 AES加密

AES 加密算法是最常见的对称加密算法，同时属于分组加密算法，它将明文分成长度相同的几组数据。且根据AES 加密的标准规范，分组长度只能是128 位。而和分组长度不同，AES 加密算法的密钥长度有3 中选择，根据AES 密钥长度的不同，加密轮数也不同[7]，如表1所示。

表1 密钥长度与加密轮数

基于AES的图像加密需要将图像的灰度值转换为矩阵形式来计算：以字节为单位对每一个4×4 的矩阵按照从左上角至右上角的顺序，依次进行AES加密；加密结束后再将分块按照加密时的顺序连接起来。得到的矩阵结果与原矩阵不同，即图像的灰度值产生了改变，得到置乱[8-9]。如果图像的灰度值不能正好转换成4×4 矩阵的形式，就需要在缺少的矩阵的右下方补零，使图像的灰度值能够转换成4×4 矩阵的形式[10]。

1.3 Tent混沌映射加密

Yoshida等分析研究了Tent 映射在其不变密度和功率谱的混沌区间中的混沌行为(具有唯一最大值的分段线性连续映射)。他们发现随着最大高度的降低，在混沌区域中发生连续的波段分离过渡，并积累到过渡点进入非混沌区域，而且非周期性轨迹的时间相关函数及其功率谱在波段分离点处及其附近进行精确计算。由于Tent映射是拓扑共轭的，因此映射的行为在这个意义上是相同的。Tent 混沌映射计算公式如下：

xi+1=f(xi,μ)

(2)

(3)

1.4 混沌双重图像加密

混沌双重图像加密算法的整体原理如图1所示。

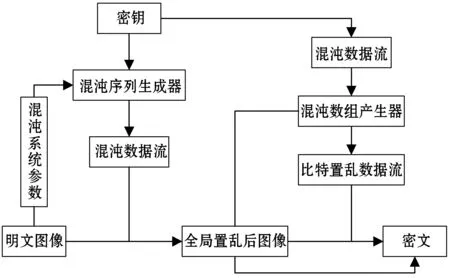
图1 混沌双重图像加密算法的整体原理

本文的混沌双重置乱加密选取是性能优良的Kent映射，其表达式为：

(4)

当x∈(0,1)、S∈(0,1)时。通过李雅普诺夫(Lyapunov)指数可以判断一个系统是否为混沌，若Lyapunov指数大于零，那就说明系统是混沌的。而Kent映射公式中就包含了一个正指数。其中初始x0可以产生的任意序列，而S为控制参数。

混沌双重置换加密[11]的过程都是可逆的，那么说明其加密的逆操作即为解密。混沌双重置换加密是先进行全局置乱，然后对每个像素值进行替代加密[12]。而其解密就是先对密文进行反替代操作，然后根据混沌数组来计算中间密文。

1.5 频域加密

频域加密是通过将图像空域和频域进行转换来实现加密的，而它们之间的转换则是利用离散余弦变换(DCT)、快速傅里叶变换(FFT)以及小波变换(WaVelet)等实现[13]。其中相较于其他变换，离散余弦变换更好。因为它能够实现图像实时压缩、抗干扰能力强，且其算法比较简单，因此它的算法复杂度较低。所以通常优先选择离散余弦变换DCT的频域加密。

加密步骤如下：首先图像转化为灰度图像，将其转换成矩阵形式；然后将这个较大的矩阵划分成 8×8 的小矩阵方块，对每个小矩阵方块都进行DCT变换；最后量化非高频系数，以此减少需要计算的数据量，再将变换后的小矩阵方块拼起来就得到了密文图像。解密时，首先将密文图像的矩阵形式划分成小矩阵方块，然后对每个小矩阵方块进行 DCT 逆变换，最后将逆变换后的小矩阵方块拼起来就得到了原始图像。

2 密文图像安全性指标参数

2.1 像素数改变率和归一化平均改变强度

像素数量的改变率NPCR和归一化平均改变强度UACI都是衡量加密算法对明文敏感度的一个指标参数。由文献[14]可知，当 NPCR接近100%、UACI接近33%时，算法对明文更加敏感，算法的抵抗差分攻击性更好。

2.2 信息熵

在Shanon的信息论中，提出了信息熵的概念,它是用来反映一个信息的不确定性，并且该指标参数也可以用来反映图像信息中的不确定性，即图像的信息熵。它可以反映出图像中灰度值的分布。经分析得出：算法的信息熵的值越大，那么经过加密后得到的密文图像的灰度值分布的就越均匀，图像像素之间的关系越无法看出来，而图像信息也就不会被轻易破译。

2.3 相邻像素之间的相关系数

若已加密图像任意方向的相邻像素对的值之间都十分分散，且无关系可寻，那么它的相关系数就越接近 0，则密文图像就越难破解。

2.4 加密耗时

加密所消耗的时间长短决定了算法的时间复杂度的大小，而时间复杂度越小，那么算法的加密所需要的时间就越短，加密过程中需要承担的风险也就更小了，则该算法的安全性较好。而时间复杂度是通过一个函数公式精确地计算出算法进行加密时所需的时间。在本文中加密时间是通过记录原始图像从开始加密到生成密文图像的时间。

2.5 密钥空间大小

密钥空间的大小的单位是位，且密钥的位越长，其空间就越大[15-16]。一个好的加密算法，密钥空间应该足够大以抵抗穷举攻击。选取混沌迭代的初始值x0和第二阶段所需的混沌系统的参数S2作为计算密钥的参数。那么在32 bit计算机中双精度数据为64 bit，则密钥空间为264×264=2 128。即便破译者一秒之内用数以亿计的密钥进行破译[17]，也需要耗时一千多年才可以把整个密钥空间破译出来。

2.6 密钥敏感性

密钥敏感性意味着如果加密密钥不同，则会产生完全不同的密文图像；类似地，如果解密密钥不同，则基于相同密文的解密结果也将不同[18]。一个好的加密算法对密钥的敏感性是十分重要的，密钥敏感性表明算法的抗选择明文/密文攻击能力。密钥敏感性值越小，则算法的抗选择明文/密文攻击能力越好。

3 方案实现

本文提出的基于多种指标参数横向比较的密文图像安全性评价方案，首先需要将选取的图像内容，按照5种不同的图像加密算法进行加密，然后由得到的密文图像计算各指标参数，并将各个指标参数与期望值对比，根据各指标参数的可靠性，判断该算法安全性。实验选取的图像内容为目前加密应用中常使用的两类“类图像”——文件照片和卫星地图照片。由于这两种图像的图像特征(颜色特征、纹理特征、形状特征和空间关系特征)和安全特性具有代表性，对其进行安全性分析得出的结论更能体现出本文方案的实用性。

3.1 图像加密

实现了Tent混沌映射加密、AES 加密、混沌双重置乱加密、仿射变换加密和频域加密这5种图像加密算法以及它们各自的解密功能。

3.2 指标参数计算

实现计算像素数改变率(NPCR)、归一化平均变化强度(UACI)、信息熵、加密时间、相邻像素之间相关系数、密钥空间大小和密钥敏感性。下面介绍部分指标参数计算方法，并由此分析各指标参数在该方案中的可靠性。

(1) NPCR与UACI：假设两个原始图像仅存在一个像素不同时，设它们的密文图像中第(i,j)点的像素值分别为C1(i,j)和C2(i,j)。若C1(i,j)=C2(i,j)，定义D(i,j)=0；若C1(i,j)≠C2(i,j)，定义D(i,j)=1。则NPCR与UACI的计算公式分别为：

(5)

(6)

式中：M和N是原始图像像素转换的矩阵的行数与列数。

由于NPCR与UACI是衡量加密算法对明文敏感度的一个指标参数，对于加密算法的安全性评判是可靠的，因此将其作为主要参数进行分析。

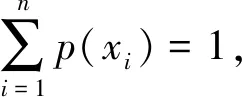
(7)

信息熵反映图像信息的不确定性，即灰度值分布的不确定性。该参数能够直接反映密文图像的安全性，是可靠的。若某加密算法的信息熵过小，则可以判断该方法是不安全的。

(3) 相邻像素之间的相关系数：首先选择N组任意图像中任意方向(水平或垂直或对角方向)的相邻像素，再通过以下公式计算相邻像素之间的相关系数：

(8)

(9)

(10)

(11)

(4) 加密耗时：在本文中加密时间是指原始图像从开始加密到生成密文图像的时间。该参数主要用于判断加密过程的速度，而不直接反映安全性，因此优先级较低。

(5) 密钥空间大小：这里以本文的混沌双重置乱加密为例，当密钥长度为r时，密钥空间有2r个元素。密钥空间足够大时可以抵抗穷举攻击，因此是可靠的。

(6) 密钥敏感性：为了更加清晰明确地反映其中密文图像的不同，通过计算不同密钥对应的密文图像与原始图像的NPCR和UACI来比较。密钥敏感性表明算法的抗选择明文/密文攻击能力，最能体现方法安全性。

综上所述，得到指标参数优先级排序。为了让评判更加全面，本文将主要参数设为：密钥敏感性、信息熵、NPCR与UACI。其余参数在使用的加密方法满足主要参数评判的安全性后，作为参考进一步比较方法的安全性。

4 实验结果

4.1 卫星地图照片

图2为一张卫星地图照片，灰度化处理后，对其依次进行Tent混沌映射加密、AES加密、混沌双重置乱加密、仿射变换加密和频域加密，得到如图3-图7所示的加密效果。

图2 原图1 图3 Tent混沌映射加密1

图4 AES加密1 图5 混沌双重置乱加密1

图6 仿射变换加密1 图7 频域加密1

通过对比，可以看出Tent混沌映射加密和AES加密的效果较好，混沌双重置乱其次。而由此得到的指标参数如表2、表3所示。由指标参数综合分析得到的结论与上文是一致的。

表2 信息熵等指标参数分析1

表3 密钥敏感性等指标参数分析1

通过对指标参数的分析，我们已知的结论有：

(1) 像素的改变率期望值为100%，为了方便，本文使用的是1-NPCR，所以该值越接近0，算法安全性越高。

(2) 归一化平均改变强度的期望值为33%，所以算法的归一化平均改变强度越接近33%，该算法安全性越高。

(3) 信息熵反映加密后图像复杂程度即图像的灰度分布情况，算法的信息熵越接近8，该算法安全性越高。

(4) 相邻像素之间的相关系数越接近0，算法安全性越高。

(5) 算法加密耗时越短，安全性越高。

(6) 密钥空间大小反映系统抗穷举攻击能力，其值越大，算法越安全。

(7) 密钥敏感性表明系统抗选择明文/密文攻击能力，其值越小，算法越安全。

以上述为前提，选取相应样本，五种加密算法的指标参数的横向比较结论如下：

加密耗时：仿射变换最快，其次是Tent混沌异或加密、频域加密、混沌双重置乱，AES最慢。

信息熵：Tent最好，其次是AES、混沌双重置乱、仿射变换加密，频域加密最差。

密钥空间大小：仿射变换加密最好，其次是AES和混沌双重置乱、Tent、频域加密。

密钥敏感性：AES最好，其次是Tent、混沌双重置乱和仿射变换、频域加密。

1-像素数改变率：频域加密较好、其次是Tent、AES、混沌双重置乱、仿射。

归一化平均改变强度：AES最好，其次是Tent、频域加密、混沌双重置乱、仿射。

相邻像素的相关系数：AES最好，其次是频域、混沌双重置乱、Tent、仿射。

综上所述，根据主要指标参数和参考其他参数可以得出，卫星地图照片加密中，不考虑加密耗时的情况下，AES最好；综合情况下Tent和AES都具有较高的安全性。

4.2 文件照片

图8为一张文件照片，步骤同4.1，得到如图9-图13所示的加密效果。

图8 原图2 图9 Tent混沌映射加密2

图10 AES加密2 图11 混沌双重置乱加密2

图12 仿射变换加密2 图13 频域加密2

可以看出Tent、AES、混沌双重置乱的加密效果相近。而由此得到的指标参数如表4、表5所示。

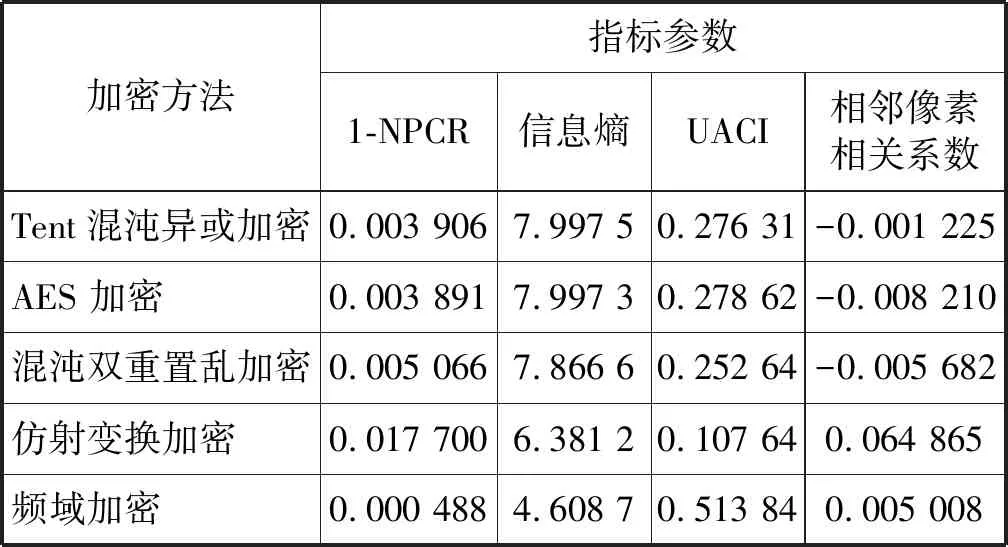
表4 信息熵等指标参数分析2

表5 密钥敏感性等指标参数分析2

由主要指标参数的横向比较得出的结论如下：

信息熵：Tent最好，其次是AES、混沌双重置乱、仿射变换加密，频域加密最差。

密钥敏感性：AES最好，其次是Tent、混沌双重置乱和仿射变换、频域加密。

1-像素数改变率：频域加密较好、其次是AES、Tent、混沌双重置乱、仿射。

归一化平均改变强度：AES最好，其次是Tent、混沌双重置乱、频域加密、仿射。

综上所述，根据主要指标参数和参考其他参数可以得出，文件照片加密中，AES具有安全性最高，Tent其次。

5 结 语

本文对五种密文图像进行基于多种指标参数的安全性评价，并由选取的两种图像样本得出相应结论：虽然两次实验结果相近(即Tent综合情况下安全性高，AES加密耗时长而安全性最高)，但具有不同图像特征和安全特性的图像，根据各指标参数分析而得到的安全性评价是不同的。本文提出的密文图像安全性评价方案，在根据需求选取不同种类的样本时，能够得出特定情况下安全性最高的图像加密算法，从而使实际应用中，选取更安全的图像加密算法，得到更好的密文图像。

本文存在的不足是在对指标参数优先级划分时，不够客观细致。下一步工作将用具体的权重划分方法，更客观全面地评判图像加密方法安全性。