基于问题等级的不完美排错NHPP可靠性模型

费 琪

(江苏自动化研究所 江苏 连云港 222061)

0 引 言

软件定义世界，在当今软件质量变得越来越重要，软件可靠性直接影响着软件质量和开发成本[1-2]，软件可靠性工程研究的重点和难点便是软件可靠性评估[3,11]。软件可靠性增长模型是软件可靠性评估的一种重要模型，通过软件可靠性增长模型对软件可靠性进行评估可以为测试工作和软件发布提供重要的参考依据。

1970年Goel和Okumoto首次使用非齐次泊松过程NHPP描述软件可靠性模型，G-O模型[4]。此后在此模型的基础上，提出了很多新模型[5-10]，经分析，这些模型存在如下缺陷：

(1) 现有的可靠性模型未与问题等级进行关联。不同的问题，测试人员故障检测率及开发人员排错率都有差别。

(2) 在对测试人员发现故障时仅考虑了测试人员的工作效率或学习能力，未与剩余的问题数进行关联。同样能力的2个测试人员在测试产品时，产品剩余的问题数越多，测试人员发现问题的概率越大，因此在考察故障检测率时不仅要考虑测试人员的学习能力，同时需考察产品的问题数。

(3) 现有模型有的假设为排错为完美排错，有的假设为不完美排错，但针对已排除的错误未考虑到错误引入率，不能对故障诊断率、错误排除率、错误引入率进行综合考察得出可靠性模型。

按照GJB2786，问题等级划分为4类：致命、严重、一般、轻微，其中针对轻微问题的定义为：“给操作员带来不方便或麻烦，但不影响所要求的运行或任务的主要功能”。为了本模型更好地建立，本文将问题等级划分为2类：轻微问题及非轻微问题。针对轻微问题及非轻微问题的特点总结如表1所示。

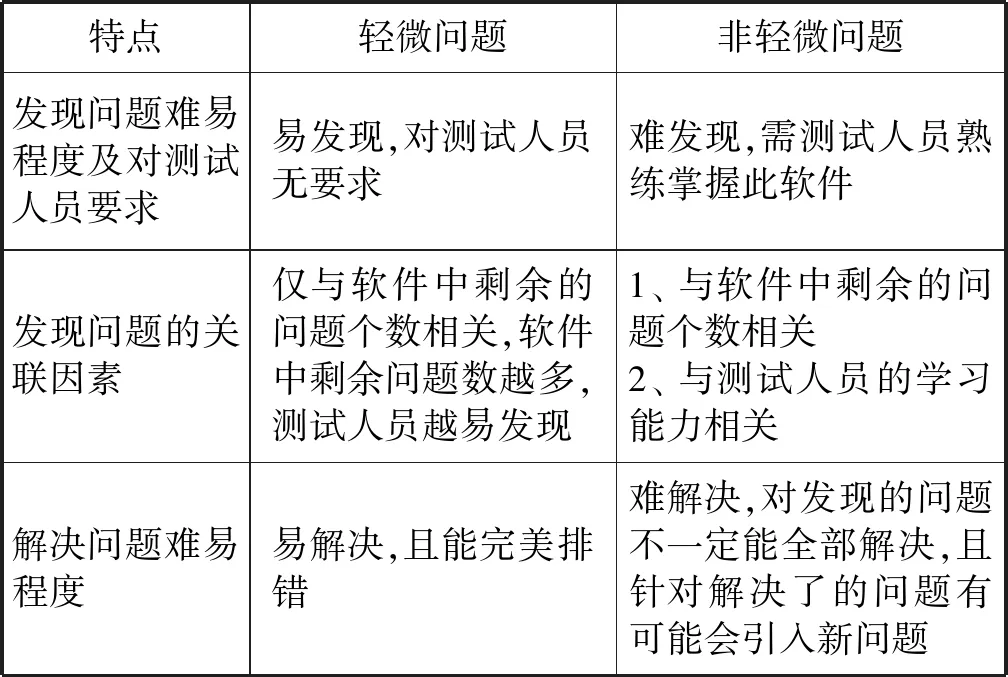
表1 问题等级及特点

1 基于问题等级的不完美排错NHPP可靠性模型建立

在构建基于问题等级的不完美排错非齐次泊松过程可靠性模型时，需做如下假设：

1) 软件运行剖面与可靠性测试剖面相同。

2) 在任意时间序列内测试人员发现的不同问题等级的故障数是相互无关的。

3) 在时刻t发现的累计错误数[E(t),t≥0]是一个随时间变化独立增长的过程，E(t)服从期望函数为L(t)的泊松分布(注：轻微问题及分轻微问题分别服从期望函数为L1(t)及L2(t)的Poisson分布)。

4) 在时间间隔(t,t+Δt)内，单位时间所发现故障数的期望值与软件残留的故障数成比例，比例为故障检测率φ(t)，0≤φ(t)≤1，针对不同问题等级的故障检测率φ(t)做如下假设：

① 在时间间隔(t,t+Δt)内软件残留的故障数越多，测试人员发现故障的概率越大。

② 针对问题等级为轻微的问题，在不同时间间隔内，测试人员发现轻微问题的概率仅与残留的故障数相关，故障检测率为φ1(t)。

③ 针对问题等级为非轻微问题，测试人员发现非轻微问题的概率不仅与残留的故障数相关而且与测试人员的学习能力相关，故障检测率为φ2(t)。

5) 在时间间隔(t,t+Δt)内，开发人员解决的错误数与单位时间内期望发现的错误数成正比，比例为错误排除率ρ(t)，0≤ρ(t)≤1，针对不同问题等级的错误排除率ρ(t)做如下假设：

① 问题等级为轻微的问题，开发人员易解决，能完全排错，错误排除率为ρ1(t)=1。

② 问题等级为非轻微的问题，开发人员不易解决，在排错过程中可能会引入新的错误，错误排除率为ρ2(t)。

6) 针对不同等级的问题，排除错误并非全是完美排错，时间t时刻预期的错误总量ω(t)与预期初始错误数α之差与排除的错误数成正比，比例为错误引入率γ(t)，针对不同问题等级的错误引入率γ(t)做如下假设：

① 问题等级为轻微的问题，开发人员排错过程中不会引入新的错误，即错误引入率为γ1(t)=0。

② 问题等级为非轻微的问题，开发人员在解决问题时有可能引入新问题，在此假设引入的新问题为非轻微问题，错误引入率为γ2(t)。

③t时刻预期的轻微问题总量为ω1(t)，初始预期错误数为α1；t时刻预期的非轻微问题总量为ω2(t)，初始预期错误数为α2。

在上述6个假设中前3个假设为NHPP可靠性模型的基本假设，后3个假设则是为反映NHPP可靠性模型与问题等级关联而特别提出的。

1.1 轻微问题NHPP可靠性模型建立

依据基于问题等级的不完美排错NHPP可靠性模型假设4)得如下方程：

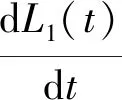
(1)

式中：ξ1(t)表示t时刻开发人员已经解决的轻微问题数。

(2)

依据基于问题等级的不完美排错NHPP可靠性模型假设6)中开发人员对轻微问题解决时不会引入新的问题，故任意时刻的问题总数与初始预期问题总数相同，即：ω1(t)=α1。

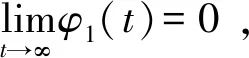
(3)

式中：λ1表示初始时刻测试人员发现轻微问题故障的检测率。

由式(1)-式(3)可得问题等级为轻微问题的NHPP可靠性模型为：

(4)

对式(4)进行求解可得问题等级为轻微问题的累计故障数为：

L1(t)=α1[1-(1+t)-λ1]

(5)

1.2 非轻微问题不完美排错NHPP可靠性模型建立

依据基于问题等级的不完美排错NHPP可靠性模型假设4)得如下方程：

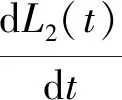
(6)

式中：ξ2(t)表示t时刻开发人员已经解决的非轻微问题数。

我的工作也不是天天去做，接了电话我便拿了门球棒到门球场去。吴小哥就是认准了门球场。虽说醒了过来，可是他的意识还很脆弱，稍一变换场景，他就会陷入糊涂中。第一次见面，我就告诫自己一定要演好这个古大富。一方面是出于对吴小哥的同情。一方面这也是我的工作。只是陪着扯扯闲篇，一个月就收入五百块，这和弯腰拾钱有啥区别。这时我又想起了那个小伙子说过的话：弯腰会不？只要弯腰，就能捡到钱。

依据基于问题等级的不完美排错NHPP可靠性模型假设5)得如下方程：

(7)

依据基于问题等级的不完美排错NHPP可靠性模型假设6)得如下方程：

ω2(t)=α2+γ2(t)×ξ2(t)

(8)

依据基于问题等级的不完美排错NHPP可靠性模型假设4)中测试人员对非轻微问题的故障检测率不仅与测试人员对软件的熟悉程度、测试人员的学习认知能力相关，而且与软件中残留的故障数相关。测试人员对软件的学习认知能力会随时间的增长而熟练，符合S型增长曲线，在此本文使用Logistic模型来描述测试人员对软件的学习能力随时间的变化，Logistic学习模型为如下方程：

(9)

式中：C表示测试人员对软件的熟悉程度，θ表示测试人员对软件的掌握速率。

(10)

开发人员对错误的排除率一般而言与时间无关，在此假设错误排除率为常数，ρ2(t)=ρ2，0≤ρ2≤1，开发人员排除错误时错误引入率与时间也无关，故假设错误引入率也为常数，γ2(t)=γ2,0≤γ2≤1。

由式(6)-式(8)、式(10)可得问题等级为非轻微问题的NHPP可靠性模型为：

(11)

对式(11)进行求解可得问题等级为非轻微问题的累计故障数为：

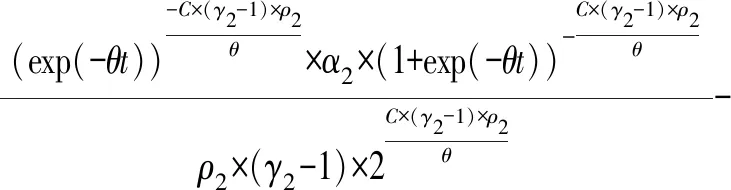
(12)

2 最大似然估计及模型求解

为了更好地预估问题等级为轻微问题及非轻微问题累计故障函数中的参数，采用最小误差平方和来计算：

(13)

式中：n为测试阶段数，ti为i阶段软件累计运行时间，yi为第i阶段发现的轻微问题数，xi为第i阶段发现的非轻微问题数，为获得轻微问题最小误差平方和，SSE1对α1、λ1求偏导，得如下方程组：

(14)

为获得非轻微问题最小误差平方和，SSE2对C、γ2、ρ2、α2求偏导，得如下方程组：

(15)

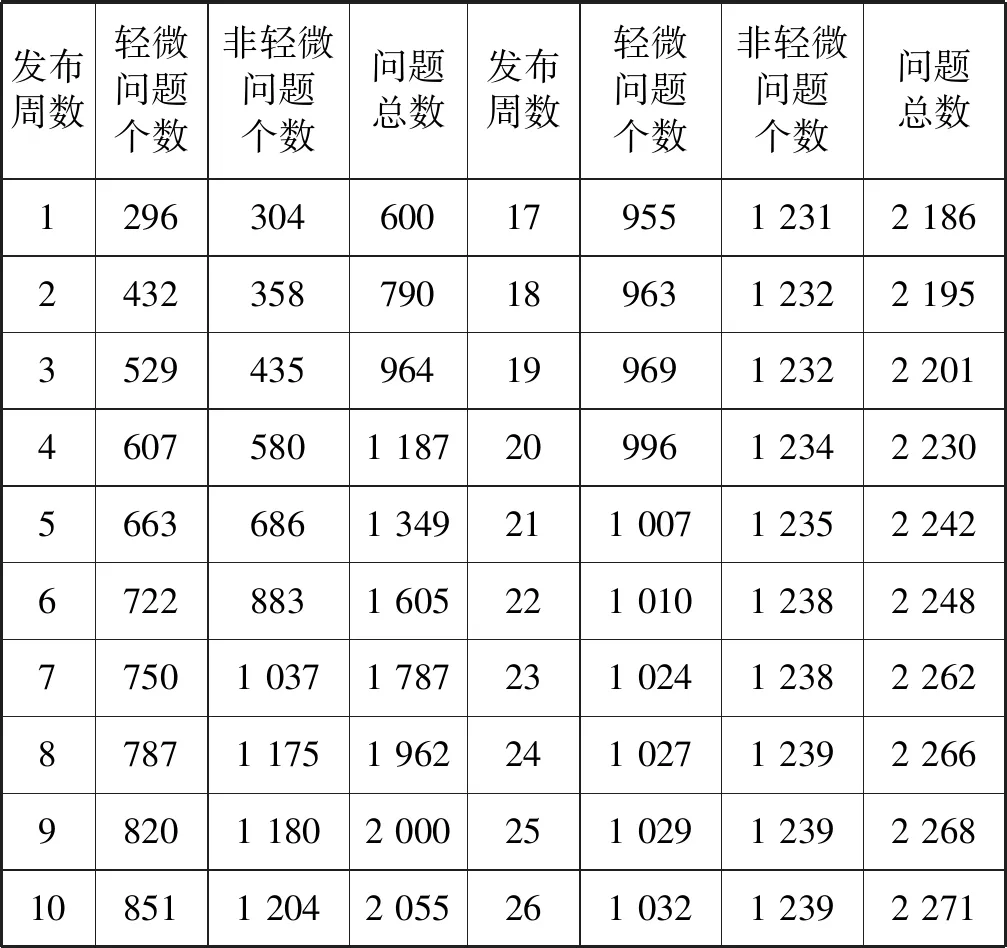
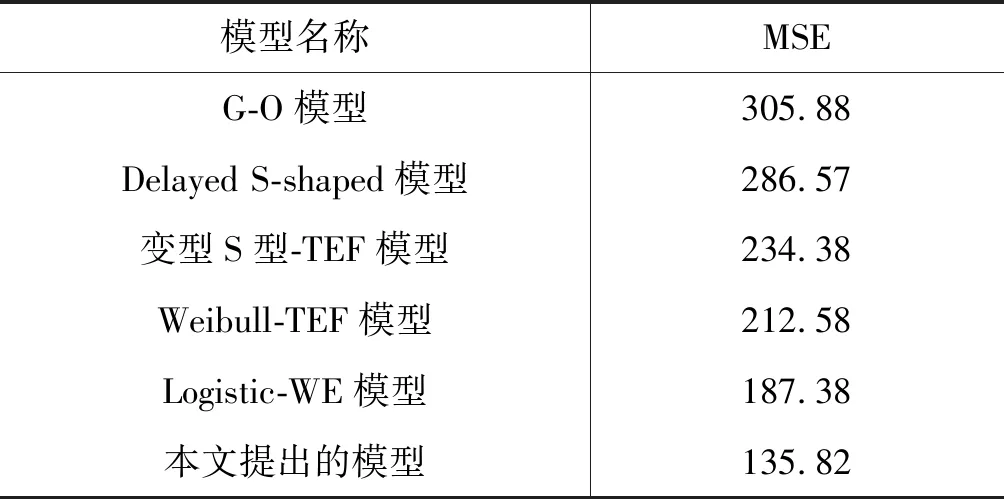
在约束条件为：0<α1<∞、0≤λ1≤1、0<α2<∞、0

L(t)=L1(t)+L2(t)=α1[1-(1+t)-λ1]+

(16)

3 实验分析

为了证明本模型的有效性，并对新模型进行评估，引入某软件测评中心针对网络管理系统的测评数据进行评估。表2给出了缺陷累积数据包括问题的发布时间及检测到不同问题等级的缺陷总数，测试团队从第1周开始测试直至第32周结束共发现问题总数为2 328个。

表2 问题缺陷统计表

续表2

针对上述数据，由式(14)可求得：α1=1 856,λ1=0.25，针对轻微问题的可靠性模型为：

L1(t)=α1[1-(1+t)-λ1]=1 856×[1-(1+t)-0.25]

(17)

由式(15)可求得：α2=835,ρ2=0.8，γ2=0.15,θ=0.15，C=0.85，针对非轻微问题的可靠性模型为：

(18)

由式(16)可求得：基于不同问题等级的不完美排错NHPP可靠性模型为：

L(t)=L1(t)+L2(t)=1 856×[1-(1+t)-0.25]+

(19)

针对问题等级为轻微时的故障拟合效果如图1所示。

图1 轻微问题故障数量拟合图

针对问题等级为非轻微时的故障拟合效果如图2所示。

图2 非轻微问题故障数量拟合图

通过MSE度量模型与G-O模型、Delayed S-shaped模型、变型S型-TEF模型、Weibull-TEF模型、Logistic-WE模型进行比较，比较结果如表3所示。

表3 MSE比较

通过以上实验分析，本文对问题等级进行分类考虑并对可靠性进行综合之后得到的预估数据拟合效果优于现有的模型。

4 结 语

本文通过分析测试人员对不同等级的问题检测率有区别，开发人员对不同等级的问题排错率不同，首次提出了基于问题等级的不完美排错NHPP可靠性模型。在考虑模型时综合考虑了测试人员的学习能力、排错率、及排错时会引入新问题的情况，更加切合实际。通过实际测试数据对本模型进行应用，并与现有模型进行比较，证明了本模型的优越性。但也有如下不足之处，在考虑开发人员对非轻微问题排错时引入的新问题为非轻微问题，而在实际中也会出现对非轻微问题的排错引入的新问题为轻微问题，针对此点还需在后续进一步进行研究。