g模糊微分方程一类边值问题解的存在唯一性

孙凤娇， 陈 峰

(河海大学 理学院，江苏 南京 211100)

在[1]中，作者研究了实值函数关于另外一个实值函数的导数，这种导数被称作g导数。g导数包含时标上的Δ导数，而且由它引出的微分方程不仅包括时标上的动态方程，也包括脉冲微分方程。对g导数的研究最早追溯到1917年[2-3]，当时学者主要为了研究Stieltjes积分相应的导数。最近，在[4]中，作者研究了实值分布微分方程、实值g微分方程和相应积分方程的等价性条件，得到了实值g微分方程解的存在性定理。

我们基于模糊值函数的g导数概念，建立了模糊值函数的g模糊微分方程，推广了一般的模糊微分方程。模糊值函数的Henstock-Stieltjes积分[5-6]对于我们的研究起到了重要的作用。

本文主要研究下述g模糊微分方程一类边值问题解的存在性和唯一性，

(1)

λx(0)=x(T),

(2)

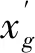
1 预备知识

E表示所有一维模糊数构成的空间。对任意α∈(0,1],u∈E,[u]α={x∈R|u(x)≥α},称为u的α—截集，它是一个闭区间。对于u,v∈E,[u+v]α=[u]α+[v]α。

定义模糊数距离如下，

其中dH表示[u]α和[v]α的Hausdorff距离[7]。在这样的距离下，E是完备的空间。

模糊数的距离有如下性质[8]:

(1)d(u+v,w+v)=d(u,w),∀u,w,v∈E；

(2)d(ku,kv)=|k|d(u,v),∀u,v∈E,k∈R；

(3)d(u+v,w+e)d(u,w)+d(v,e),∀u,w,v,e∈E。

我们称映射f:[a,b]→E为一个模糊值函数。对任意ε>0,如果存在δ>0,使得对t∈[a,b],只要|t-t0|<δ,都有d(f(t),f(t0))<ε,则称模糊值函数f在t0∈[a,b]是连续的。如果f在[a,b]上任一点都是连续的，则称f是[a,b]上的连续模糊值函数。我们用C([a,b],E)表示定义在[a,b]上的所有连续模糊值函数。(C([a,b],E),dC)是完备的半线性空间[8][9]，其中dC定义如下，

模糊数的减法运算由加法运算引出，我们先给出模糊数的加法运算[8]。设u,v∈E,

设模糊数u,v∈E,如果存在w∈E,使得u=v+w,那么我们称w为u和v之间的差，记为w=u⊖v。在本文中，“⊖”表示模糊数之间差的运算，注意到u⊖v≠u+(-v)。

则称函数f在t0点是g可微的。

引理1[5]设模糊值函数f和h是关于定义在[a,b]上的实值增函数g是Henstock-Stieltjes模糊可积的，则下述性质成立：

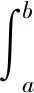
引理2[5]设f:[a,b]→E关于定义在[a,b]上的实值增函数g是Henstock-Stieltjes模糊可积的，若g是连续的，则

也是连续的。

引理3[6]设g:[a,b]→R是定义在[a,b]上的实值有界变差函数，{fn}是定义在[a,b]上关于g的Henstock-Stieltjes模糊可积函数列。若fn一致收敛于f,则f在[a,b]上关于函数g是Henstock-Stieltjes可积的且

引理4[10]若f是定义在[a,b]上的实值正则函数，g是定义在[a,b]上的实值有界变差函数，则

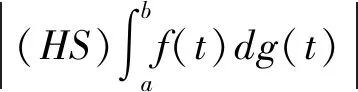
定义2[11]若存在一个紧集K⊂R,使得对A⊆E中的任意元素u,均有[u]0⊆K,则称A具有紧支集。

定义3[11]设A⊆E,若对任意ε>0,存在δ>0,使得对任意u∈A,存在α0∈[0,1],只要|α-α0|<δ,都有dH([u]α,[u]α0)<ε,那么称A在α0上是截集等度连续的。如果A在任意α0∈[0,1]都截集等度连续，那么称A在[0,1]上截集等度连续。

定义4[11]设f:[a,b]×E→E,如果对任意I⊆[a,b]和有界子集A⊆E,都有f(I×A)在E中相对紧，则称连续映射f:[a,b]×E→E是紧的。

引理5[9]设A是E中的子集，A在E中相对紧等价于A在E中具有紧支集且A在[0,1]上截集等度连续。

引理6[11](Ascoli-Arzelá) 设X是紧的距离空间，Y是距离空间，M⊆C(X,Y),则M是相对紧的，当且仅当下列条件成立：

(1)M等度连续；

(2)对任意α∈X,集合E(a)={f(a)|f∈M}在Y中相对紧。

引理7[9](Schauder不动点定理) 设X是具有消去性的半线性空间，M是X中的非空有界闭凸子集，若T:M→M是一个紧算子，则T在M中至少有一个不动点。

注1当x满足下面的积分方程，λ≠1时，

2 解的存在性

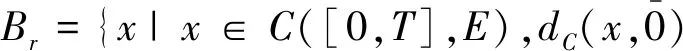
在λ>1时,我们有如下存在性结论：

定理1若f:[0,T]×E→E满足下列条件：

(1)对于任意x∈C([0,T],E),f(t,x(t))关于g是Henstock-Stieltjes可积的；

(2)对任意t∈[0,T],f(t,·)连续；

(3)f是紧的；

则方程(1)-(2)至少存在一个解。

证明定义一个算子T如下，

则由于g是连续的，由引理2知Tx(t)也是连续的。由注1知，算子T的不动点就是问题的解。接下来我们证明算子T有不动点。

第一步T(Br)⊆Br。

对任意t∈[0,T],x∈Br,借助引理1和模糊数距离的性质我们有

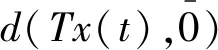
r。

第二步T(Br)相对紧。

对任意t∈[0,T],x∈Br,借助引理1和模糊数距离的性质我们有

d(Tx(t),Tx(t0))

由于g连续，当t→t0时，d(Tx(t),Tx(t0))→0。于是T(Br)是等度连续的。

设Ω={x(t)|t∈[0,T],x∈Br}。由于f是紧的，则由引理5知f([0,T]×Ω)具有紧支集且截集等度连续，因此有紧集K,使得对任意t∈[0,T],x∈Br,我们有[f(t,x(t))]0⊆K。并且对任意ε>0,存在δ>0,当|α-β|<δ,我们有dH([f(t,x(t))]α,[f(t,x(t))]β)ε。于是当|α-β|<δ时，有

dH([Tx(t)]α,[Tx(t)]β)

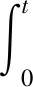
可知T(Br)(t)是截集等度连续的，并且有紧支集。由引理5知，对任意t∈[0,T],T(Br)t是紧的。另外由Ascoli-Arzelà定理知，T(Br)相对紧。

第三步 算子T是连续的。

综上，由Schauder不动点定理可知，算子T在Br中至少存在一个不动点，也就是方程(1)-(2)的解。

在0<λ<1时，我们有如下存在性结论：

定理2若f:[0,T]×E→E满足下列条件：

(1)对于任意x∈C([0,T],E),f(t,x(t))关于g是Henstock-Stieltjes可积的；

(2)对任意t∈[0,T],f(t,·)连续；

(3)f是紧的；

由于证明过程与定理1类似，在此省略定理2的证明过程。

3 解的唯一性

当λ>1时，我们有如下唯一性定理：

定理3f:[0,T]×E→E是连续的，若对任意的x,y∈C([0,T],E),x≠y,t∈[0,T],都有d(f(t,x(t)),f(t,y(t)))kd(x(t),y(t)),其中k满足则方程(1)-(2)的解是唯一的。

证明定义一个算子T如下，

假设x1,x2都是方程(1)-(2)的解，借助引理4我们有

d(x1(t),x2(t))=d(Tx1(t),Tx2(t))

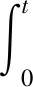
当0<λ<1时，我们有如下唯一性定理：

定理4f:[0,T]×E→E是连续的，若对任意的x,y∈C([0,T],E),x≠y,t∈[0,T],都有d(f(t,x(t)),f(t,y(t)))kd(x(t),y(t)),其中k满足则方程(1)-(2)的解是唯一的。

由于定理4的证明过程和和定理3的证明过程相似，在此省略定理4的证明。