Beta回归模型基于EM算法的变量选择方法

王 玲， 赵为华

(南通大学 理学院，江苏 南通 226019)

引 言

在对众多领域的实际问题进行统计分析时，取值在(0,1)区间上的比例数据是很常见的，比如股息率、考试通过率、工作效率、次品率以及资本比率等。对于(0,1)上的连续分布，最简单明确的方法是线性回归建模，并用普通最小二乘法估计回归系数。然而线性回归并不能保证拟合值或预测值完全落在区间(0,1)内，这使得结果很难解释，还会产生异方差问题。因此对分数响应变量建模时，直接线性回归是不合适的。为此，Ferrari 和CribariNeto(2004)针对这样的响应变量提出了Beta回归模型，对Beta分布的密度函数进行参数重变换后，y～Beta(μ,φ),即

其中0<μ<1，φ>0,通过链接函数建立了Beta均值回归模型

(1)

其中β=(β0,β1,…,βk)T是一个未知回归参数向量，x1,…,xk是k个解释变量。由于Beta分布是一个双参数的分布，因此利用Beta回归刻画比例数据具有很好的灵活性。

在初始回归建模时通常引入许多解释变量去拟合响应变量。然而，这些潜在的解释变量中通常只有一小部分对响应变量有影响，而大部分解释变量的影响都是非常小甚至为零的。选择重要的变量以达到精简模型、提高预测精度近年来成为重要的话题。已有的很多文献都是基于惩罚函数的正则化变量选择方法，如LASSO，SCAD、MCP等罚函数方法。就基于Beta回归模型的变量选择而言，方匡南和王秉权(2016)基于SCAD罚函数方法研究正则化Beta回归；Zhao等(2014)基于坐标算法提出了变散度Beta回归模型的变量选择问题。事实上，变量选择问题是一个有挑战性的任务，在任意实际数据集中，真实的回归系数要么为零要么很大是不可能的，通常是趋向于零。因此，问题不在于找到零系数，而是找到那些足够小到可以认为不重要的系数，把它们缩小到零。最近兴起的贝叶斯变量选择方法相比于基于惩罚函数的变量选择方法具有更多的优势，主要体现在：(1)惩罚函数的变量选择方法需要选择惩罚参数，惩罚参数通常通过一些准则或交叉核实方法获得，惩罚参数选择的好坏影响最终的结果，对于复杂的模型很难得到满意的结果，而贝叶斯方法通过选取合适的先验进而通过后验分布的抽样或经验贝叶斯方法获取，得到的结果相对比较可靠；(2)贝叶斯变量选择方法能得到参数的全后验分布而不是单个估计值，因而对估计参数的了解更全面，进而易得参数的可信区间估计及其他感兴趣变量的估计；(3)对于小样本数据，经典的统计方法往往不够准确,贝叶斯方法由于利用数据的先验信息从而使得估计和推断精度较高。近几年贝叶斯变量选择方法受到广大研究者的青睐，在计量经济、金融统计、数据挖掘、模式识别、人工智能等领域有很好的应用。基于随机搜索的贝叶斯变量选择方法最早由George和Mcculloch(1997)提出，是一种目前比较流行的贝叶斯变量选择方法。

1 Beta回归模型

由于从得分方程Uβ(β,φ)=0和Uφ(β,φ)=0中无法直接得到β和φ的极大似然估计的确切表达式，因此需要使用数值计算方法最大化对数似然函数来获得，通常可以使用牛顿算法或者拟牛顿法进行迭代直至收敛。R语言中软件包“betareg”可以获得β和φ的极大似然估计。

2 基于EM算法的贝叶斯变量选择

为应用贝叶斯变量选择方法，我们引进一个二进制指示向量γ=(γ1,…,γp)′,γi∈{0,1},其中γi=1表示模型中包含第i个变量xi。选取β的spike-and-slab高斯混合先验

π(β|σ2,γ,v0,v1)=Np(0,Dσ2,γ)

其中Dσ2,γ=σ2diag(a1,…,ap),ai=(1-γi)v0+γiv1,0v0v1。假定σ2的先验服从逆伽马分布π(σ2)=IG(v/2,vλ/2)。对于散度参数φ,假定其先验服从伽马分布π(φ)=Ga(ν/2,νλ/2)。对于指示变量γ=(γ1,…,γp)′,γi∈{0,1},取

π(γ|θ)=θ|γ|(1-θ)p-|γ|

π(β,φ,θ,σ2,γ|y)=p(y|β,φ)×π(β|σ2,γ)×π(σ2)×π(γ|θ)×π(θ)

由于指示变量γ总共有2p个可能取值，相当于有2p个候选模型需要选择，因此直接应用基于随机搜索的贝叶斯变量选择方法(SSVS)计算量特别大。EMVS基于EM算法替代常用的MCMC随机搜索方法，将指示变量γ视为潜在变量，对联合后验分布的对数似然取期望得到目标函数

Q(β,φ,θ,σ2|β(k),φ(k),θ(k),(σ2)(k))=Eγ|.[logπ(β,φ,θ,σ2,γ|y)|β(k),φ(k),θ(k),(σ2)(k),y],

其中Eγ|.(·)表示条件期望Eγ|β(k),φ(k),θ(k),(σ2)(k),y(·),通过重复最大化目标函数来间接最大化π(β,φ,θ,σ2|y)。在第k次迭代，给定(β(k),φ(k),θ(k),(σ2)(k)),首先是E-步骤，计算目标函数右边的期望来获得Q。接着是M-步骤，在(β,φ,θ,σ2)下最大化Q来产生(β(k+1),φ(k+1),θ(k+1),(σ2)(k+1))的值。

目标函数Q可以进一步写成如下形式

Q(β,φ,θ,σ2|β(k),φ(k),θ(k),(σ2)(k))

=C+Q1(β,φ,σ2|β(k),φ(k),θ(k),(σ2)(k))+Q2(θ|β(k),φ(k),θ(k),(σ2)(k))其中

Q1(β,φ,σ2|β(k),θ(k),φ(k),(σ2)(k)

Q2(θ|β(k),θ(k),φ(k),(σ2)(k)

下面给出E-步和M-步的快速计算形式。

E-步

其中

M-步

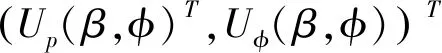
对于Q2,其最大化是通过下面的表达式获得的，

重复以上E步和M步，直至各参数收敛。

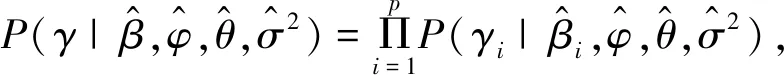
则有

ci≥di

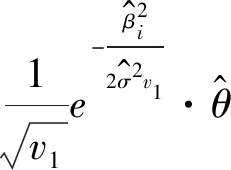
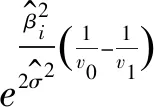
所以可以得到

上式即为第i个变量是否进入最终模型的门限值，在应用中很容易实施。

3 实例分析

这一节我们将使用前面提出的变量选择方法对中国上市公司的股息率及其影响因素进行分析。股息率指以年化基准表示的投资、基金或投资组合的预期派息总额，再加上投资者在该期间可能获得的任何额外的非经常性股息。根据公司的偏好和战略，股息率可以固定或调整。现金流动性强的公司通常会派发股息，而快速增长的公司则会将产生的现金重新投资于业务，并不向股东派发任何股息。股息率是衡量企业投资价值的重要指标。因为沪深300指数覆盖了沪深两个证券市场大部分的流通市值，能够反映市场主流投资的收益情况，所以这里选取沪深300指数的300只成分股作为研究对象。数据来源于wind金融数据库。

影响上市公司股息率的因素有很多，根据金融方面的相关资料，我们选取了19个变量(见表1)，分别从上市公司的资本规模、市场表现、投资潜力、盈利能力、风险系数、偿债能力等多角度反映公司的情况。当我们试图确定如何最有效地使用自变量来模拟或分析多元回归模型时，解释变量之间存在的高度相关关系会扭曲或误导结果。这样的多重共线性通常会导致解释变量的置信区间变大，可靠概率值(P值)变低。不相干变量进入最终模型，不仅干扰对变量间关系的理解，还费时费力，因此筛选掉不相干变量是非常有必要的。

表1 变量解释及说明

表2 参数估计结果及变量选择

续表2变量系数估计是否进入模型资产负债率(%)β120.00000总资产周转率(%)β130.00060每股收益同比增长率β140.08331净资产同比增长率β150.18551税后每股股利β160.21421年度分红总额β170.000103年累计分红占比(%)β180.75921每股现金净额β19-0.00070φ275.4165θ0.4501门限值0.0097

表2给出了这种变量选择方法下各参数的估计值，得到门限值为0.0097，并认为如下变量应该进入最终模型：年涨跌幅、市净率、机构评级、净资产收益率、每股收益同比增长率、净资产同比增长率、税后每股股利及3年累计分红占比，而其他变量则认为对股息率没有显著影响。年涨跌幅是对涨跌值的描述，表现价格波动情况；市净率则表示该股票的投资潜力；机构评级是指由信用评级机构对股票进行的等级评定，体现了市场评价；净资产收益率直接反映了上市公司的盈利能力，而盈利能力体现着上市公司投资价值，决定了企业的投资价值；每股收益同比增长率反映了每一份公司股权可以分得的利润的增长程度，很好的体现了公司的成长能力；净资产同比增长率反映了企业的发展能力，高而稳定的增长率是显而易见的期望结果；税后每股利体现了企业的分红政策；3年累计分红占比则体现了再融资条件。