基于线性正弦跟踪算法的PMSM无位置传感器研究

何继爱，郁 琪，李婕妤，马 云

(1.兰州理工大学, 兰州 730000;2.中山市普阳电子科技有限公司,中山 528400)

0 引 言

内置式永磁同步电机(以下简称IPMSM)具有高功率密度、高效率等优点，在工业领域扮演重要角色[1]。在采用磁场定向矢量控制时，为了实现高性能的三相永磁同步电机控制系统，一般都需要获取准确的转子位置及转速信息，但机械传感器的安装使用会增加成本，占用空间，并对使用环境有比较严格的要求[2-3]。高频信号注入法的基本思想是把一个高频电压(电流)信号叠加到基波信号上，相应的高频电流(电压)信号中将携带转子位置信息，通过适当的信号处理就能估计出转子的位置[4-5]。

目前，常用的注入高频信号主要有旋转高频电压信号[6]和脉振高频电压信号[7]。脉振电压信号注入法可以用于凸极率很小甚至表贴式永磁同步电机转子位置检测，但是转子位置信息提取的快速性和准确性对高频注入法位置跟踪性能有极大的影响。文献[8-9]设计了基于锁相环(PLL)的转子位置跟踪方法，并将PI调节器和其串联构成PLL系统，可以快速准确地跟踪转子位置。文献[10]采用基于跟踪观测器的转子位置估计方法，对转子位置实现了较好的跟踪。以上方法虽然可以实现转子位置的快速跟踪，但是为了获得角度误差，要预先对高频响应电流进行幅值调制和低通滤波处理，增加了运算量。

本文基于脉振高频电压信号注入法，对IPMSM模型进行研究分析，将电力系统中对电信号的分析方法线性正弦跟踪(LST)算法[11]引用到转子位置跟踪中，设计了LST位置跟踪器，不需要对高频响应电流进行幅值调制和低通滤波，就可以直接提取转子角度误差，从而实现永磁同步电机的无位置传感器控制。

1 脉振高频电压信号注入法的原理

1.1 永磁同步电机数学模型

内置式三相永磁同步电机在旋转坐标系下的电压方程：

(1)

定子磁链方程：

(2)

将式(2)代入式(1)，电压方程可变成：

(3)

式中：ud，uq分别是定子电压的d，q轴分量；id，iq分别是定子电流的d，q轴分量；R是定子电阻；ωe是电角速度；Ld，Lq分别是d，q轴的电感分量；ψf代表永磁体磁链。

转矩方程：

(4)

式中：Te为电磁转矩；p为电机极对数。

1.2 脉振高频电压激励下的永磁同步电动机电流响应

当电机运行于低速区且注入信号频率远高于电机运行频率时，永磁同步电机可以近似等效为纯电感模型。此时式(3)可以简化：

(5)

式中：udh，uqh为d，q坐标系定子高频电压分量；idh，iqh为d，q坐标系定子高频电流分量；Ldh，Lqh为d，q坐标系定子高频电感。

图1 几种坐标系间关系

(6)

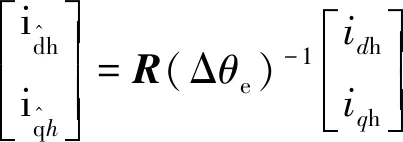
式中：

(8)

(9)

(10)

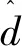
(11)

式中：uin为高频电压信号的幅值；ωin为高频电压信号的频率。

此时，式(10)可以简化：

(12)

将q轴高频响应电流单独列写如下:

(13)

2 线性正弦跟踪算法

2.1 线性正弦跟踪的原理

线性正弦跟踪(以下简称LST)算法可以实现对正弦信号幅值和相位的估计，根据最小方差原则和梯度下降法，再经过旋转变化，得到线性常微分方程，从而设计线性正弦跟踪器。当输入正弦信号的角频率等于滤波器的频率参数，则滤波器输出能够实现对输入的无幅值误差、无相位误差跟随[10]。目前，LST算法主要应用于电力系统中对电信号的分析。

假设已知频率为ωo的单个正弦信号表达式：

u(t)=Usin(ωot+δo) (-π≤δo≤π) (14)

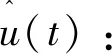
(15)

把式(14)展开得到：

u(t)=Ucosδosin(ωot)+Usinδocos(ωot)(16)

(17)

幅值的估计值a(t)：

(18)

信号的估计误差e(t)：

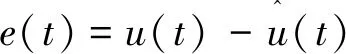
(19)

根据最小均方误差思想，定义代价函数：

根据以上分析可以看出，流域内大部分区域作物都存在不同程度作物缺水情况，但是不同分区缺水的原因也有所区别。

(20)

采用随机梯度下降法，并且每个状态的变化方向为J(y)对该状态的梯度的负方向：

(21)

μ为矩阵，调节y(t)收敛到最优值的速度以及算法的稳定性。令μ1>μ2>0，选择：

(22)

得到周期系数线性动力系统：

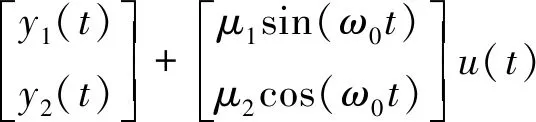
y(t)做旋转变换，令：

(24)

代入式(23)可得：

(25)

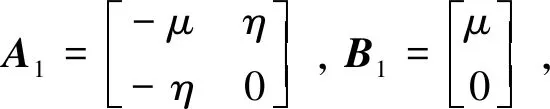
(26)

(27)

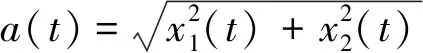
由式(28)可以对信号的幅值进行计算跟踪。

2.2 LST算法的稳定性证明

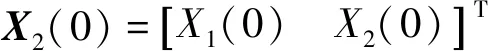
(30)

对式(30)进行Laplace变换，有：

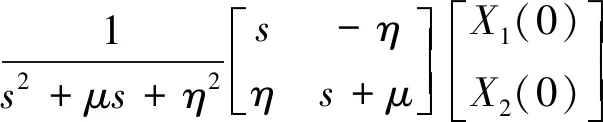
对式(31)进行Laplace逆变换，有三种情况：

(1)当μ=2η时，有：

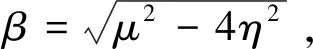
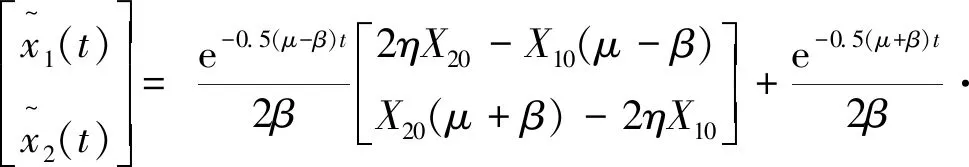
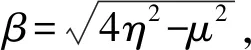
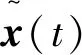
3 仿真与分析

由LST算法直接跟踪式(13)的高频响应电流的幅值变化，提取角度误差值Δθe，并将其调节至0，那么Δθ也将为0，此时转子位置的估计值收敛到转子位置实际值。基于LST算法的脉振高频电压信号注入法原理，如图2所示，其中T3s/2s表示三相坐标系转换到静止坐标的变换矩阵；T(θe)表示静止坐标系转换为旋转坐标系的变换矩阵；T-1(θe)为旋转坐标系转换为静止坐标系的变换矩阵。

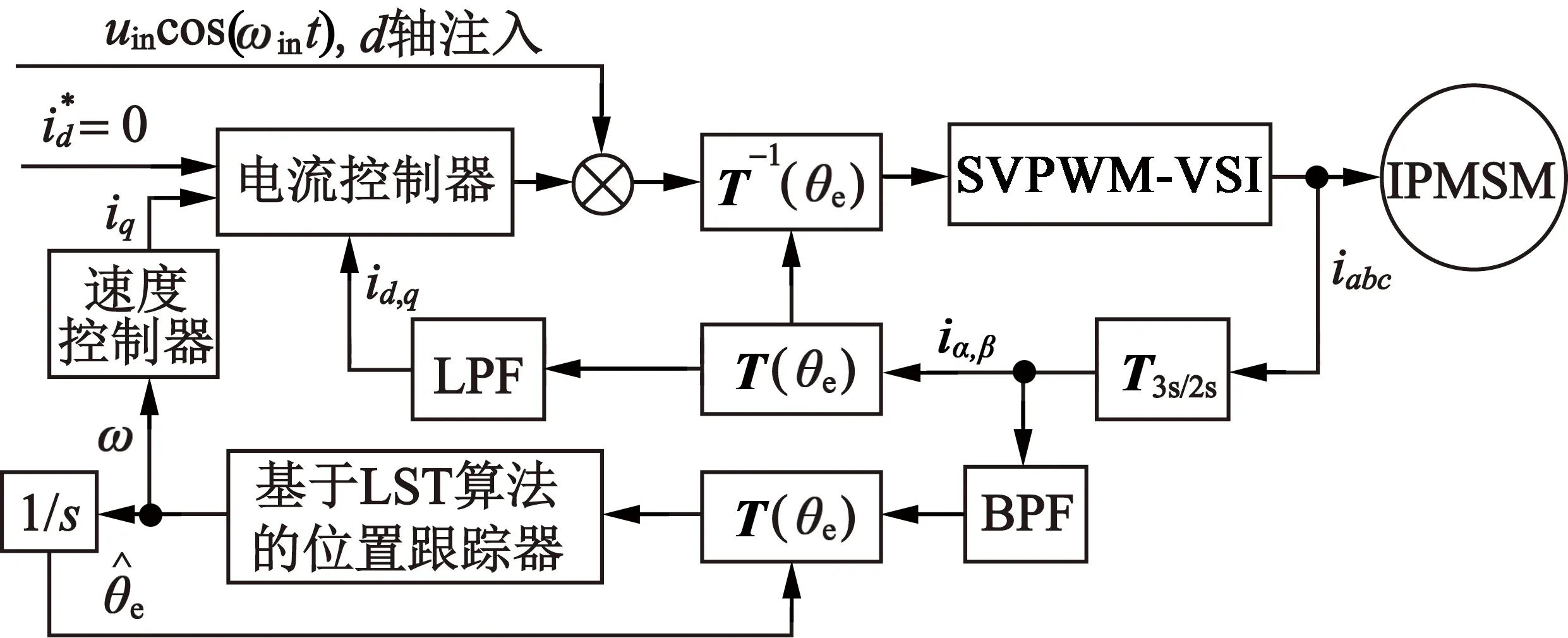
图2 基于LST算法的脉振高频电压信号注入法原理框图

为了验证该方法的可行性，在MATLAB/Simulink环境下搭建系统仿真模型，电机仿真参数如表1所示。脉振高频电压信号的幅值uin=20 V，频率ωin=1 000 Hz，低通滤波器(LPF)的设计采用巴特沃斯方法，阶数为1，通带频率为150 Hz。带通滤波器(BPF)的设计采用巴特沃斯方法，阶数为2，低通带边缘频率为987 Hz，高通带边缘频率为1 018 Hz。仿真条件：采用变步长ode45算法，相对误差为0.001，仿真时间为1 s。

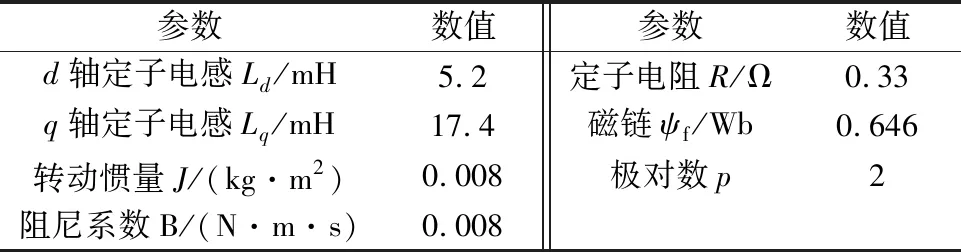
表1 电机仿真参数

在参考转速为100 r/min的空载运行下，图3为转子位置估计和实际值的对比图，从图3可以看出，估计值和实际值基本吻合。图4为位置估计误差，由图4可以看出估计误差小于1°(1 rad≈57.3°)，表明估计转子位置能够实时反映转子的实际位置。

图3 转子位置对比图

图4 位置估计误差

图5为电机转速估计值与实际值的对比图，从图5中可以看出，估计转速响应速度快，超调小，较快地稳定在额定转速值。图6为转速估计误差，由图6可以看出，在开始阶段，转速估计误差较大，稳定之后，在转速100 r/min时估计误差可以控制在0.02 r/min的范围内，说明估计转速可以真实地反映实际转速值，可用于电机的无位置传感器控制。

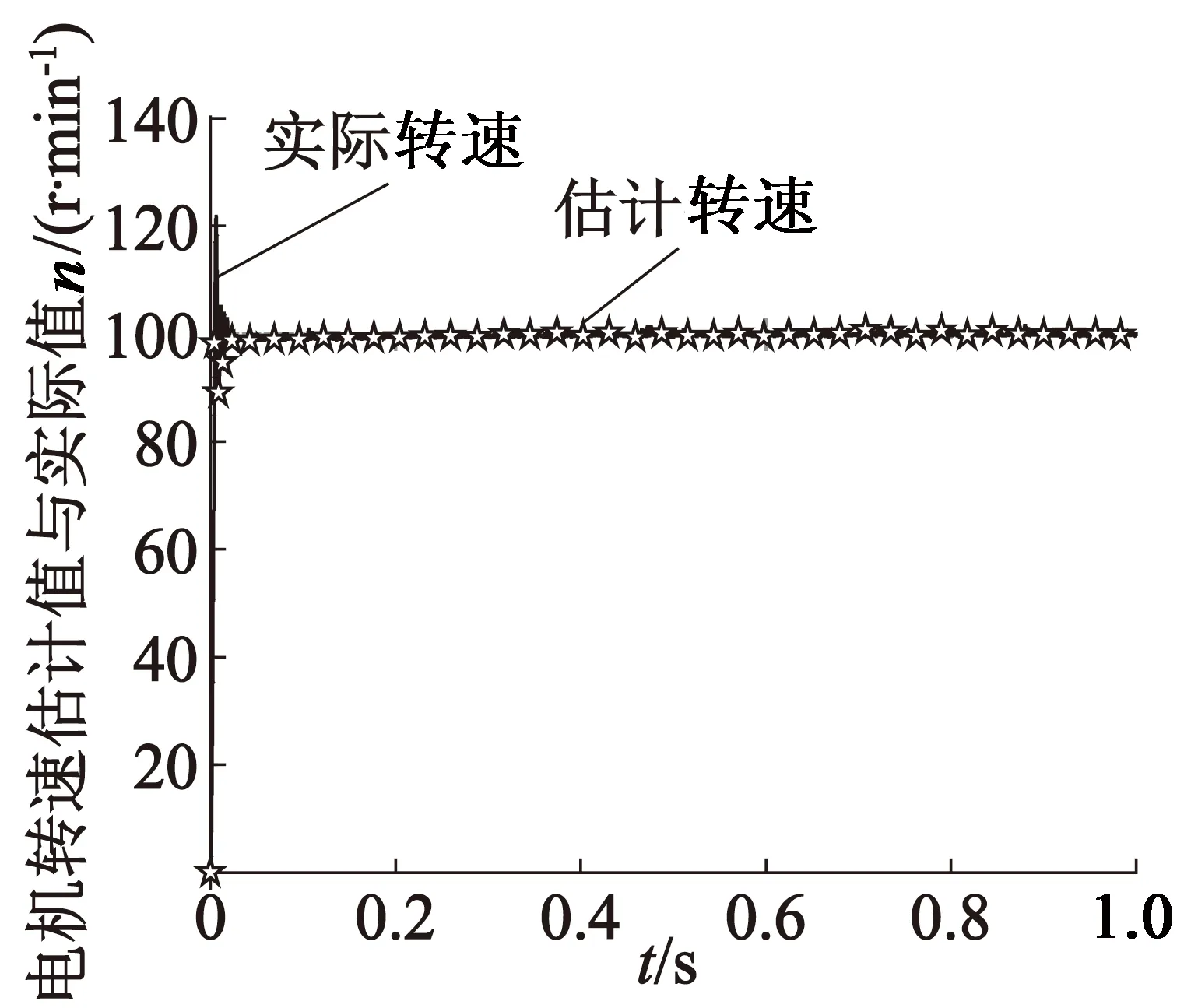
图5 电机转速对比图

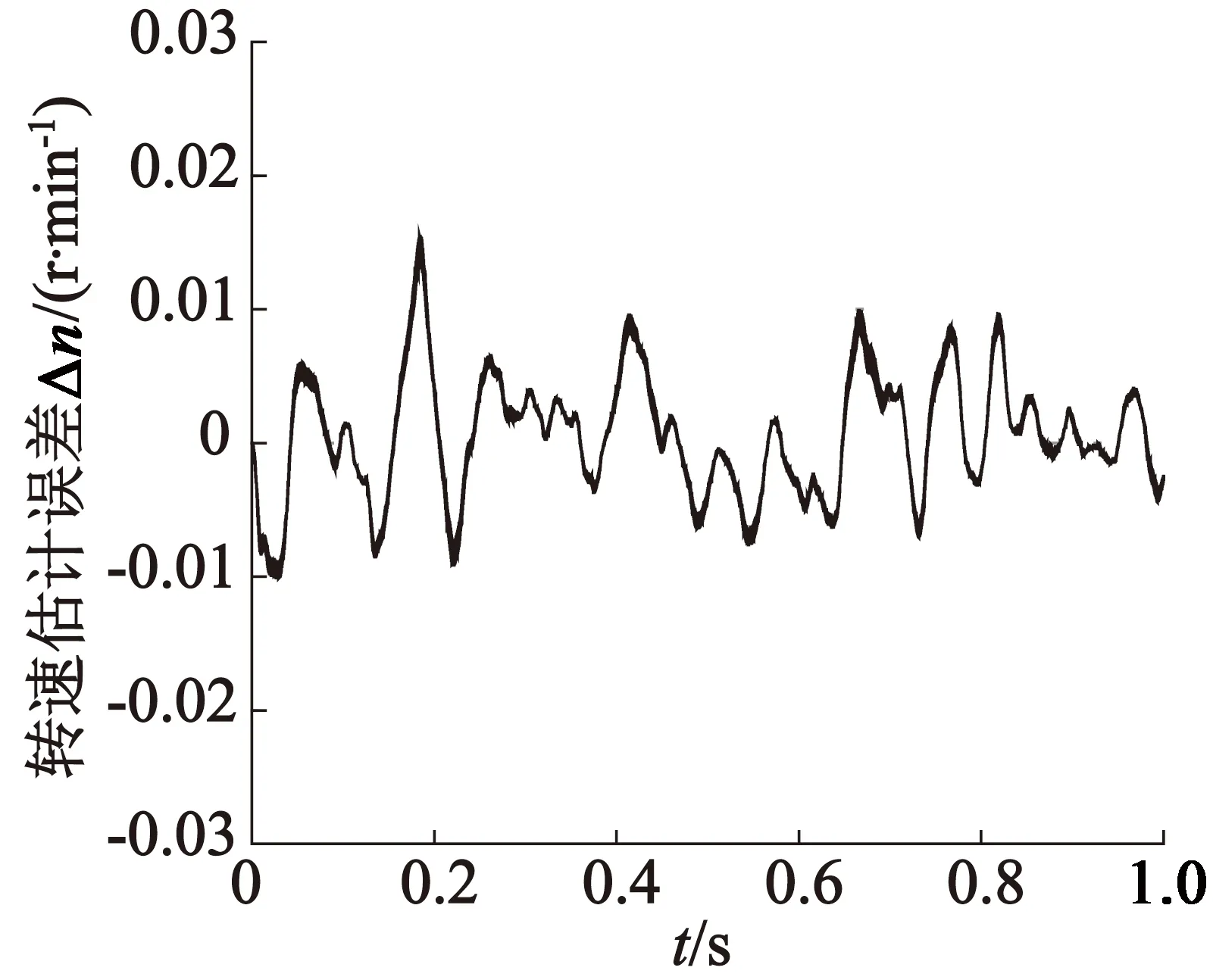
图6 转速估计误差

4 结 语

本文对脉振高频电压信号注入法在永磁同步电机无位置传感器控制的应用进行了研究分析，将电力系统中对电信号的分析方法——LST算法运用到电机控制系统，简化系统结构，提高系统性能，实现了转子误差角度的快速准确提取，并通过仿真验证了该方法的有效性，为永磁同步电机无位置传感器控制提供了一种新的途径。